基于无限边坡模型和概率理论的区域边坡可靠度计算研究

高焕翔，何宇康，张 彪，李文彬，黄发明

(1.南昌大学前湖学院,江西 南昌 330031；2.南昌大学建筑工程学院,江西 南昌 330031)

边坡失稳通常是指斜坡上的岩土体在各种因素影响下失去原有稳定状态，随重力作用沿滑动面整体或分散下滑的现象[1]。我国国土面积中约70%为山地丘陵地区，其受边坡失稳的危害较大，当地居民的生命和财产遭受了严重的威胁[2]。因此，开展区域边坡稳定性及其可靠度计算，能够为国家在山地丘陵地区的规划和建设提供依据，促进我国防灾减灾工作的发展。

随着现代计算机技术的发展，边坡稳定性及可靠性分析逐渐向与计算机技术相结合的方向发展。如郭奥飞[3]采用有限元分析法研究了边坡稳定可靠度，虽具有较高的可靠性，但分析过程中需要边坡的应力-应变等数据，存在数据难以获取且计算过程较复杂的问题；Zhu等[4]、Huang等[5]提出的并行递归新型神经网络算法、自编码器神经网络算法等，虽能够避免陷入局部最优解并获得较好的预测结果，但存在模型建立过程复杂、运算过程难以详细探究等问题；操丽等[6]提出的模糊逻辑法以及陈新宇等[7]提出的模糊综合评价法操作较为简单且运算速度快，但该方法较为主观，其预测结果受人为因素的影响较大。上述研究为区域边坡稳定性及可靠性研究打下了坚实的基础。

近年来，基于无限边坡模型延伸出了SINMAP模型[8-9]、SHALSTAB模型[10]和TRIGRS模型[11]等物理模型，传统的物理模型虽然能够考虑较多的地质因素且地质参数较容易获取，但受到模型公式的数学性质的影响，均存在着低坡度区边坡稳定性计算结果随坡度变化不稳定、中高坡度区边坡稳定性随坡度增大而单调下降以及计算结果未考虑地质条件的时间和空间变化等问题。为了解决这些问题，本文提出了一种基于无限边坡模型和概率理论的边坡可靠度计算新模型(Regional Infinite Slope and Probability theory based slope Reliability Mapping,RISPRM)。RISPRM模型在无限边坡模型的基础上，引入土体抗剪强度与地形坡度的关联性分析[12]和基于概率论的蒙特卡洛方法，既包含了物理模型，具有能够考虑较多地质参数的优点，又通过边坡土体抗剪强度参数与地形坡度的关系对边坡土体抗剪强度参数的空间分布规律进行了修正，弥补了传统物理模型在数学性质上的缺陷以及对于地质参数时空变异的忽视。

综上所述，本文拟通过创新性地开发RISPRM模型来开展区域边坡可靠度计算，并与代表传统物理模型的SINMAP模型的计算结果进行对比分析。最后以江西省赣州市宁都县为研究区，分别采用两种模型对该区域边坡稳定性或可靠度进行计算，并通过两种模型的频率比和预测率曲线精度对比来验证RISPRM模型的预测效果。

1 RISPRM模型的基本原理与实现步骤

1.1 无限边坡模型计算边坡稳定性

RISPRM模型首先基于无限边坡模型理论[13-14]，假设所计算边坡为平行于地表面的软弱结构面且忽略其边缘作用；然后考虑到与边坡稳定性有关的边坡土体黏聚力等主要参数[15]，引入动水压力对边坡稳定性[16]的影响，并定义边坡抗滑力与滑动力之比为边坡稳定性系数，其计算公式如下：

(1)

式中：c为边坡土体的黏聚力(Pa)；θ为边坡的地形坡度(°)；ρs为自然状态下边坡土体的密度(kg/m3)；g为重力加速度(m/s2)；D为边坡土体的垂直厚度(m)；Dw为土层等压面间的垂直距离(m)；ρw为水的密度(kg/m3)；φ为边坡土体的内摩擦角(°)。

在本模型中，假设边坡土体中存在不透水层且土层较薄，其力学模型见图1。将公式(1)化简，可得到下式:

(2)

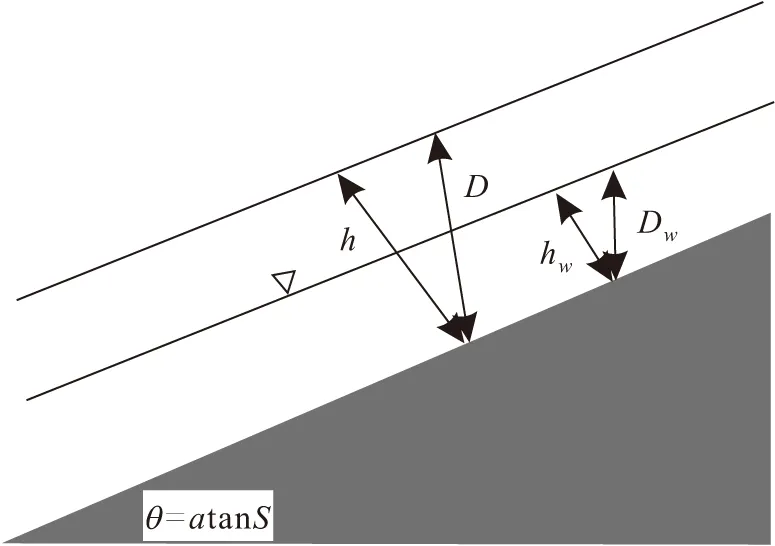
图1 基于无限边坡模型和概率理论的边坡力学模型 示意图Fig.1 Schematic diagram of slope mechanical model based on infinite slope and probability theoretical model

1.2 概率理论修正无限边坡模型

对公式(2)所计算的边坡稳定性系数所表示的含义，采用无限边坡模型常用的分级标准加以界定[17]，见表1。

表1 边坡稳定性分级标准Table 1 Standard of slope stability classification

由表1可知,当SI>1.5时，该区域便属于“极稳定区”[18]。因此，当SI>2×1.5时，该地区边坡必然处于无条件稳定状态。而对于SI计算值大于3，则没有实际的边坡可靠度分析参考价值。另外，根据无限边坡稳定性系数计算值与边坡坡度的相关性可知，边坡地形坡度在0°～60°范围内时，无限边坡模型所计算的边坡稳定性系数SI值随地形坡度的增大而单调递减。因此，若对全部输入无限边坡模型的边坡地形坡度值θ增加一个合适的定值优化坡度α，使得计算坡度变为(α+θ)，即可跳过公式中SI值大于3的无意义计算区间且不会影响计算结果的趋势。由此进一步优化公式(2)，可得到考虑定值优化坡度α的边坡稳定性系数计算公式为

(3)

本文基于公式(3)，再针对无限边坡模型存在所计算的SI值随坡度增大而单调递减这一不符合实地调查情况的问题，利用边坡土体抗剪强度与边坡地形坡度的关系对边坡土体主要抗剪强度参数c、φ进行修正，并将修正后的边坡土体抗剪强度参数cs、φs代入公式(3)中，即可弥补无限边坡模型“在低坡度区边坡稳定性计算结果随坡度变化极不稳定且快速下降”和“边坡稳定性计算结果随坡度增大而单调递减”这两大缺陷。弥补结果见下式，此公式即为基于RISPRM模型的边坡稳定性系数计算公式：

(4)

1.3 基于概率论的蒙特卡洛法基本原理

本文基于RISPRM模型的边坡稳定性系数计算公式，采用基于概率论的蒙特卡洛法[19]考虑边坡土体抗剪强度参数的空间变异性，开展了边坡可靠度计算。边坡稳定性系数可表示如下：

SI=g(X1,X2,…,Xn)

(5)

式中：SI为边坡稳定性系数,SI的计算采用公式(4);X1,X2,…,Xn为n个对边坡稳定性有影响的主要变量，如边坡地形坡度、边坡土体黏聚力及内摩擦角、地形湿度指数等。

采用基于概率论的蒙特卡洛法进行抽样模拟计算时，应在合理范围内随机生成地形参数，形成一组样本值X1i，X2i，…，Xni，并代入公式(4)求得该组样本值对应的边坡稳定性系数SIi，以此方式重复N次，便可得到N个相对独立的边坡稳定性系数SI1,SI2,…,SIn。由统计学理论可知，当N足够大时，根据SI1,SI2,…,SIn即可求得边坡稳定性系数SI的分布，其均值和标准差分别如下：

(6)

(7)

边坡稳定性系数SI服从正态分布，定义边坡可靠度指标为β，有：

(8)

另外，边坡失稳概率Psi为

Psi=1-φ(β)

(9)

式中：φ(β)为标准正态分布函数。

每个Psi与唯一的β对应，并将Psi定义为边坡最终的可靠度指标。

1.4 RISPRM模型的实现步骤

RISPRM模型的实现流程(见图2)如下：

(1) 获取研究区内各栅格单元中影响边坡稳定性的主要地质参数φ、c′、w、r和θ。

(2) 计算研究区全部栅格单元的SI值，并定义所有SI≥3的栅格单元中最大的栅格单元坡度为定值优化坡度α。

(3) 通过研究区野外调研获取的边坡与坡度之间的频率比关系，找到频率比快速下降的临界地形坡度θ′，并令大于θ′的实际地形坡度θ等于θ′后代入边坡稳定性系数计算公式。

(4) 取宁都县部分区域的边坡土体主要抗剪强度参数c′、φ与对应的地形坡度进行拟合，并使用拟合得到的关系式对宁都县全域边坡土体抗剪强度参数c′和φ′值进行修正，再将修正后的边坡土体抗剪强度cs、φs代入边坡稳定性系数计算公式。

(5) 对于各栅格单元保持其边坡计算坡度θ(θ≤θ′)、定值优化坡度α以及参数w、r不变，对其边坡土体抗剪强度参数cs、φs值进行蒙特卡洛随机提取，每随机提取出一组值便代入新的边坡稳定性系数计算公式，以便计算出该栅格单元的一个SI值。对该区域内各栅格单元重复随机抽取计算1 000次。

(6) 结合概率论分析各栅格单元的1 000次抽样模拟结果，得出各栅格单元边坡最终的可靠度指标(即Psi)。

图2 RISPRM模型的实现流程图Fig.2 RISPRM model implementation flow chart

2 研究区概况及地质参数分析

2.1 研究区概况

本文以江西省赣州市宁都县为研究区，采用RISPRM模型对该区域边坡可靠度进行计算，并与代表传统物理模型的SINMAP模型的计算结果进行分析与对比，以验证RISPRM模型的可靠性和可行性。

宁都县属于江西省赣州市，全境地质构造较为复杂，同时具有隆起、凹陷、褶皱及断层。该地区地处中亚热带季风湿润气候区，4～6月降水量占全年降雨量的40%～70%，降雨较为集中。根据野外调查、遥感影像以及过往的历史记录所确定的边坡点分布(见图3),自1970年以来，宁都县共有边坡446个，这些边坡主要分布在宁都县南端以及西南和东南区域，在县域中部以及北部分布较少。边坡体主要以第四纪堆积层为主，边坡类型主要是小型浅层覆盖型边坡，运动方式主要为牵引式整体滑动。该区域边坡失稳的主要诱发因素是季节性强降雨和不合理的工程建设。

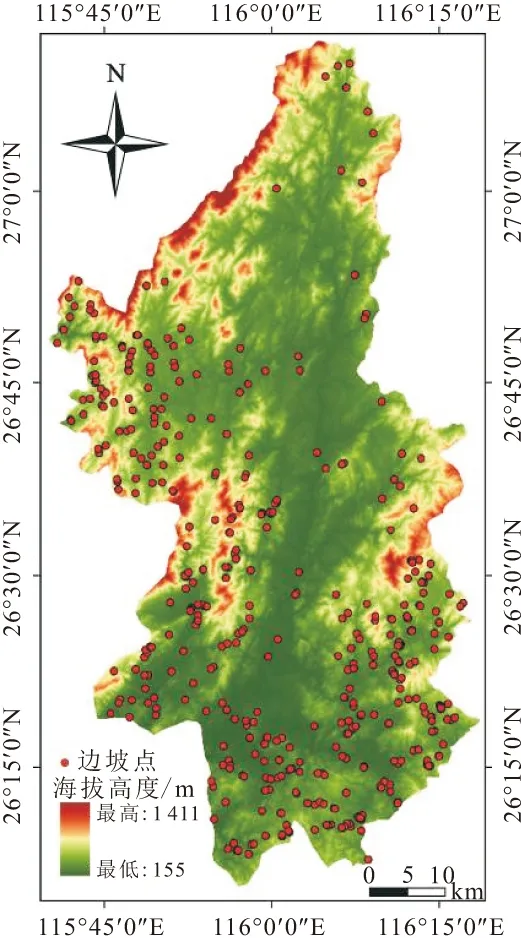
图3 宁都县高程及边坡编录Fig.3 Elevation and landslide cataloging in Ningdu County

2.2 影响边坡稳定性的主要地质参数分析

经分析可知，影响该区域边坡稳定性的主要地质参数包括原始地形坡度、地形湿度指数、边坡土体黏聚力及内摩擦角、水土容重比[20]，其分布见图4。

由图4可见，研究区边坡点所在位置大多分布在边坡岩土体黏聚力、内摩擦角较小的区域；地形湿度指数对边坡稳定性的影响相对上述两者而言较小；地形坡度对边坡稳定性存在一定的影响，但并非服从“地形坡度越大，边坡越发育，边坡稳定性越差”这一单调关系。

2.3 滑坡发生频率比与地形坡度的关系分析

滑坡发生的频率比(FR)反映了边坡在各环境因子子类别的分布状况，揭示了各环境因子子区间对滑坡发育的影响程度。滑坡发生的频率比FR的计算公式为

(10)

式中：s′表示单个环境因子的一个属性区间内的边坡面积(m2);S′表示研究区内边坡的总面积(m);s表示该属性区间的面积(m2);S表示研究区总面积(m2)。

FR值大于1，表示对应的环境因子子区间利于发生滑坡事件的发生；而FR值小于1，表明发生滑坡的概率较小。

滑坡发生的FR与地形坡度的关系见图5。

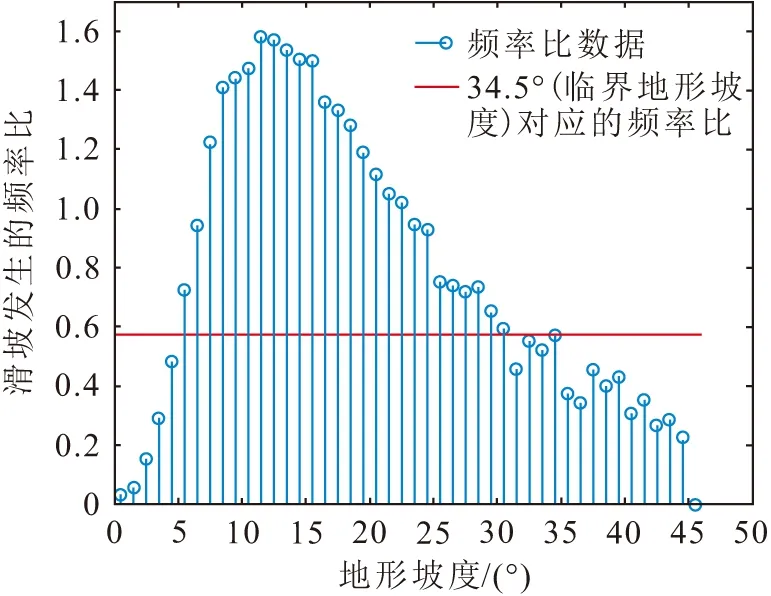
图5 宁都县滑坡发生的频率比与边坡地形坡度的 关系图Fig.5 Relationship between frequency ratio and slope topographic gradient of Ningdu County

由图5可见，存在滑坡发生的FR值快速下降的临界地形坡度θ′，当地形坡度大于θ′时，地形坡度的增大对滑坡发生的促进作用较小。在较大的地形坡度区域中，地形坡度的增大而滑坡发生的FR值下降的主要原因之一是高地形坡度区域的松散堆积层易被流水或其他自然因素冲刷掉，使得该区域的剩余土体均为抗剪强度较高的堆积层。可见，在较高地形坡度区域内，相对地形坡度而言，边坡土体抗剪强度成为影响边坡稳定性的主要控制因素。

3 研究区RISPRM模型的建立与求解

3.1 研究区初始边坡稳定性系数计算

图6 宁都县全域和某栅格的SI-θ曲线Fig.6 SI-θ curves of the whole area and a grid unit of Ningdu County

采用公式(2)计算宁都县1 132 091个栅格的初始边坡稳定性系数SI值后，并绘制其SI-θ散点图，其结果见图6(a)。同时，在宁都县全部栅格的地形参数中进行多次随机抽取，每次抽取的地形参数中仅对边坡地形坡度值θ进行修改，并绘制出该栅格于θ∈[1°,60°]范围内的SI-θ曲线。由于多次抽取地形参数后计算所得的SI-θ曲线的趋势和结果范围几乎一致，故在此处仅列出宁都县某一栅格的SI-θ曲线，见图6(b)。

由图6可以明显看出，仅依据无限边坡模型建立的初始边坡稳定性系数计算公式存在以下两大问题：①当边坡地形坡度处于0°～10°时，由初始边坡稳定性系数公式计算出的SI值随地形坡度的变化极其不稳定，呈现“断崖式”下降，且计算所得的SI值几乎都在3以上；②根据初始边坡稳定性系数公式计算的结果，当边坡地形坡度处于0°～60°时，SI值随地形坡度的增大而持续下降[21]。结合上述对比分析可知，依据无限边坡模型建立的初始边坡稳定性系数计算公式，由于其数学性能上的缺陷，与边坡实际地质情况间存在一定误差，需进一步完善。

3.2 研究区定值优化坡度的求解

由前文可知，当SI值大于3时其不再有实际的边坡可靠度分析参考价值，所以本文选择研究区内所有SI≥3的栅格单元最大坡度值(见图7),并将该地形坡度值定义为公式(3)中针对宁都县区域的定值优化坡度α。另外，由定值坡度优化后研究区SI-θ曲线[见图8(a)]可知，经α修正后的SI值收敛至0.264 8～2.767 4，即说明通过定值优化坡度α对初始边坡稳定性系数计算公式的完善，能够较好地解决其原本在地形坡度0°～10°内边坡稳定性计算结果极不稳定且研究意义不大的问题。

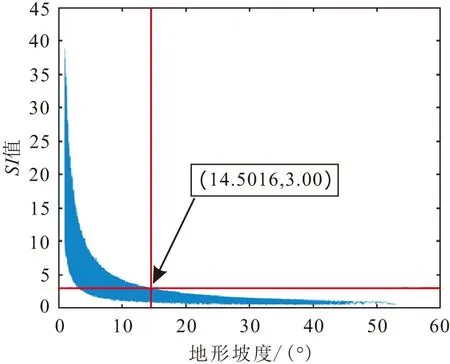
图7 宁都县定值优化坡度α搜寻原理图Fig.7 Schematic diagram of searching fixed value to optimize slope α of Ningdu County

3.3 研究区边坡土体抗剪强度参数的修正

如前所述，初始边坡稳定性系数计算公式在0°～60°地形坡度内时，存在所计算的SI值随坡度增大而单调递减这一不符合实地边坡调查情况的问题，而在较高地形坡度区内，相对地形坡度而言的边坡土体抗剪强度成为影响边坡稳定性的主要控制因素。故依据边坡土体抗剪强度参数c与地形坡度的关系对边坡土体抗剪强度参数c′和φ，进行修正，主要步骤如下：

(1) 研究区栅格以地形坡度为依据进行划分，从0°开始，每隔约10°取一划分点，划分点的选取可在主观上适当波动，以通过随机性避免数值拟合样本选取的偶然性。

(2) 统计所选取的划分点上下0.5°范围内c′和φ′的均值，作为该划分点对应的c′和φ′值。

(3) 对上一步中所选取的划分点样本以幂函数形式对边坡土体抗剪强度参数-地形坡度进行数值拟合，得到c′和φ′值以(θ=0,c′=c0)和(θ=0,φ′=φ0)为第一数据点时，随坡度增幅的函数解析式fc(θ)和fφ(θ)。则当地形坡度为θ时，某栅格考虑地形坡度的边坡土体抗剪强度修正值如下式

cs=c′-c0+fc(θ)

(11)

φs=φ′-φ0+fφ(θ)

(12)

依据上述步骤求解后，即可由公式(4)求得宁都县的SI-θ曲线，见图8(b)。

由图8(b)可见，由RISPRM模型所得的边坡稳定性计算结果不仅落在具有实际参考意义的范围内，而且当实际地形坡度较高时，所计算的SI值也随地形坡度的增大而增大，更加符合实地调研情况。

3.4 利用基于概率论的蒙特卡洛法计算研究区边坡可靠度

在边坡稳定性计算的基础上，采用基于概率论的蒙特卡洛法[22]计算宁都县边坡可靠度，并分析区域边坡土体力学参数的空间变异性特征。首先设定各栅格的地形坡度θ、地形湿度指数w和水土容重比r[23]不变；然后将各栅格的边坡土体抗剪强度参数c′和φ′修正为cs和φs，利用MATLAB软件产生范围在[-5，5]的伪随机数，将其与cs和φs相加以实现栅格内边坡土体抗剪强度参数的随机变化；最后使用RISPRM模型公式计算各栅格的SI值。本

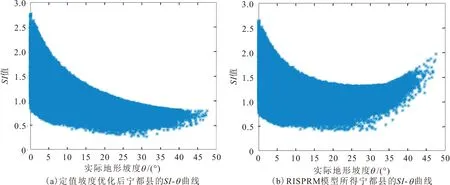
图8 定值坡度优化后和RISPRM模型得到的宁都县SI-θ曲线Fig.8 SI-θ curves of Ningdu County optimized by fixed slope value and calculated by RISPRM model

文对各栅格进行1 000次随机计算，可得到各栅格SI的均值和方差，再利用基于概率论的蒙特卡洛法计算出宁都县的边坡失稳概率即边坡可靠度，并绘制滑坡易发性分布图，见图9(a)。

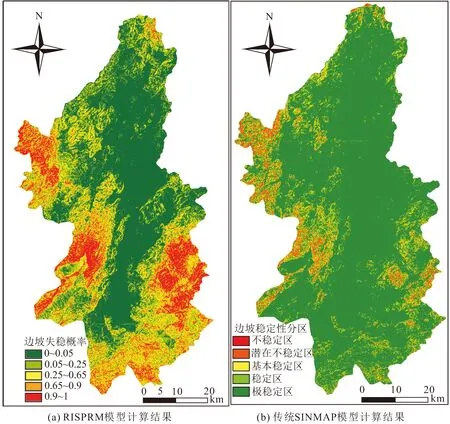
图9 RISPRM模型和传统SINMAP模型计算得到的宁都县滑坡易发性分布图Fig.9 Landslide reliability map of Ningdo County calculated by RISPRM model and SINMAP model

4 传统SINMAP模型计算研究区滑坡易发性

4.1 SINMAP模型的参数及计算结果

依据SINMAP模型的基本原理[24]，整理出宁都县边坡地形坡度θ、边坡土体黏聚力c及内摩擦角φ、边坡土体容重比r，上述三项边坡土体力学参数由宁都县土样的室内试验测出。对于导水系数T、有效降雨量q和比集水面积a，由于其参数获取较为复杂且计算误差较大，本文采用ArcGIS软件计算出地形湿度指数w来替换T，极大地简化了计算过程且获取了较为可信的水流变化特征。另外，需将地形湿度指数w控制在[0,1]范围内，w大于1的部分将形成地表径流，因此将大于1的地形湿度指数设定为1。最后按SINMAP模型公式导入相关参数，将计算所得的边坡稳定性系数按表1进行分级，绘制边坡稳定性分区图，见图9(b)。

4.2 SINMAP模型的计算结果分析

对比图3和图9可见，RISPRM模型与SINMAP模型的计算结果相比，RISPRM模型在边坡区域分布的预测准确性上有明显提升，尤其是在宁都县南部地区。而由图3可见，宁都县南部地区边坡分布密度较高，但SINMAP模型的计算结果却显示该区域边坡大多为“极稳定区”[见图9(b)]；而RISPRM模型较好地计算出了该区域边坡的不稳定性。

从SINMAP模型的频率比精度分析结果(见表2)可知，SINMAP模型计算出的研究区中处于极不稳定与不稳定区的栅格单元数共134个，占宁都县总面积的0.011 8%，而SINMAP模型预测结果中处于该区域的边坡栅格单元数和频率比均为0，虽然这一极端结果与该区域本身的样本栅格单元数量偏少有关，但也反映出SINMAP模型在高危灾害区的预测效果不理想;对于潜在不稳定区、基本稳定区和稳定区而言，SINMAP模型在该区域的频率比在[1.060 9～1.107 6]范围内变化且波动幅度较小，表明SINMAP模型在滑坡中等易发区内的性能发挥平稳但不够优越；另外对于极稳定区，SINMAP模型在该区域的频率比降至0.981 8，表明SINMAP模型在该区域的预测性能下降。综上所述，SINMAP模型对研究区边坡稳定性的总体预测性能不够理想。

表2 SINMAP模型的频率比精度分析结果Table 2 Analysis result of frequency ratio accuracy of SINMAP model

5 讨 论

5.1 两种模型频率比精度对比分析

SINMAP模型的频率比精度[25]分析结果见表2，RISPRM模型的频率比精度分析结果见表3。为了便于比较两种模型的预测性能，依据表1中边坡稳定性分级标准，综合自然间断点法和基于概率论的蒙特卡洛法计算结果，对RISPRM模型的计算结果进行了划分。

表3 RISPRM模型的频率比精度分析结果Table 3 Analysis result of frequency ratio accuracy of RISPRM model

对比表2和表3可知，RISPRM模型在“极不稳定与不稳定区”的频率比为1.753 0，而SINMAP模型在该区域的频率比为0，可见RISPRM模型对于高危灾害区的预测效果相对SINMAP模型有极大的提升；同样地，在“潜在不稳定区”和“基本稳定区”，RISPRM模型的预测效果也明显优于后者；而在“稳定区”和“极稳定区”内，虽然RISPRM模型的预测精度低于SINMAP模型，但对整体预测精度的影响不大。综上所述，RISPRM模型的预测准确性和实用性均优于SINMAP模型。

5.2 两种模型的预测率曲线精度对比分析

采用预测率曲线法[25]对宁都县1 132 091个栅格的边坡稳定性系数FS和蒙特卡洛边坡失稳概率分别进行降序排列，然后将排序后的两个指标数值在GIS软件中以5%的间隔划分为20等份，再根据研究区内发生滑坡的栅格落入各等间隔区间内的比例来判别两种模型的预测率曲线精度，其结果见图10。

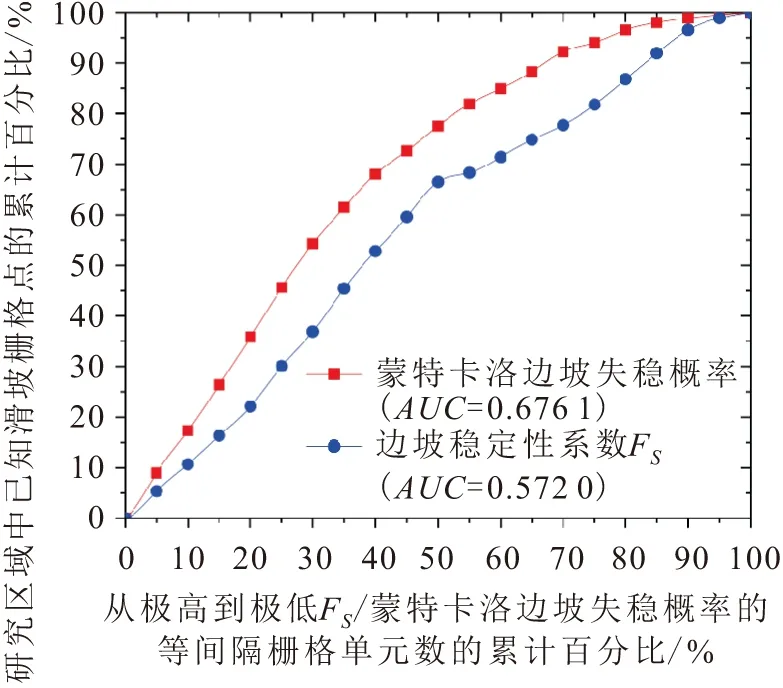
图10 RISPRM模型和传统SINMAP模型的预测率 曲线对比Fig.10 Comparison of prediction rate curves between RISPRM model and SINMAP model

由图10可见,RISPRM模型的预测效果几乎在整个研究区内都明显优于传统SINMAP模型。整体而言，蒙特卡洛边坡失稳概率和边坡稳定性系数FS的预测率分别为67.61%和57.20%，由此可见RISPRM模型的预测效果明显优于传统SINMAP模型。

5.3 RISPRM模型建模讨论

虽然RISPRM模型与传统SINMAP物理模型相比其预测精度提升显著，但未能完全避免其计算结果受边坡地形坡度的影响较大这一问题，可见仍需要继续改进。频率比分析结果显示RISPRM模型虽然在中、高危险区的预测性能优异，但对于低危险区的预测效果却不太理想。这可能是由于RISPRM模型所引入的优化方法对低坡度区效果不佳，从而使得低危险区的计算结果未能体现出本模型对传统无限边坡物理模型的优化效果。

此外，RISPRM模型仅通过单一的地形湿度指数来衡量土中水的影响，而没有考虑降雨等因素,因此在影响边坡稳定性的参数选择和取值方法上仍需要继续改进。由于本实验所使用的硬件水平限制，对蒙特卡洛模拟的次数偏少，可能会造成实验结果不够精准，没有完全发挥出RISPRM模型的预测能力，这也将是今后需要改进的方面。

6 结 语

(1) 传统无限边坡模型的边坡稳定性计算结果在低坡度区内存在随坡度变化不稳定等缺陷。针对这一问题，利用边坡稳定性系数曲线的单调性以定值坡度对其进行修正，能够在不影响边坡稳定性系数整体变化趋势的情况下得到更有参考价值的计算结果。

(2) 传统无限边坡模型的边坡稳定性计算结果在中高坡度区存在随坡度增大而单调下降，这不符合边坡野外分布的实际情况。RISPRM模型考虑高坡度区内边坡土体抗剪强度较高这一事实，引入土体抗剪强度参数与坡度的计算修正关系对传统无限边坡模型进行修正，所得的边坡稳定性计算结果更符合实际情况。

(3) RISPRM模型包含了传统物理模型公式可解释性强、所需地形参数较少的优点，并且结合了基于概率论的蒙特卡洛方法，使得模型构建更加符合实际情况。RISPRM模型在预测精度上比SINMAP等传统物理模型有显著的提升，尤其是对中、高危险区的预测性能更优。