Fibonacci多项式的置换性质

王智坚

(四川大学数学学院， 成都 610064)

1 引 言

对非负整数n，Fibonacci多项式fn(x)是由如下递推关系给出的整系数多项式：

f0(x)=0,f1(x)=1,

fn(x)=xfn-1(x)+fn-2(x),n≥2.

由于fn(1)=fn-1(1)+fn-2(x)，这正好是Fibonacci数的递推关系，即 Fibonacci多项式可以看作是Fibonacci数的推广.当x=2时，fn(2)=2fn-1(2)+fn-2(2).此时fn(2)便是著名的Pell数.

Fibonacci多项式是比利时数学家Catalan和德国数学家Jacobsthal在1883年首先提出来的[1].有关Fibonacci多项式的一般性质，尤其是算术性质，已得到广泛的研究[2-3].

设p为素数，e为正整数.若有限域Fpe上的多项式f(x)作为Fpe上的多项式函数诱导出Fpe的一个双射，则称f(x)为Fpe上的置换多项式.置换多项式在代数学、组合学、数论、编码理论、密码学等领域中均有广泛而又重要的应用. 如何判定和构造置换多项式始终是置换多项式研究领域的主要课题.

Fibonacci多项式原本定义在整数环上，它们自然可以被视为任何有限域上的多项式，从而可讨论它们在有限域上的置换性质.最近，Koroglu，Ozbek及Siap[4]研究了有限域上以Fibonacci多项式为生成多项式之一的循环码.Kitayama和Shiomi[5]研究了有限域上Fibonacci多项式的不可约性.

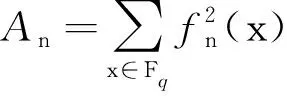
2 整环上的Fibonacci多项式

设D为特征不为2的整环，K为它的分式域.在没有混淆的情况下，我们以f简记K上的多项式f(x).

由Fibonacci多项式的定义，易见每个Fibonacci多项式均定义在整数环Z上，从而可定义在任何交换环上[6].我们首先将Fibonacci多项式看成定义在整环D上的多项式.

类似于Fibonacci数列，我们可以得到[7]

其中α+β=x,αβ=-1.不失一般性，可取

引理2.1对于整环D上的Fibonacci多项式列{fn}，有

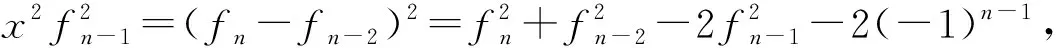
对于D上的多项式列{φn}，定义它们的生成函数为

这是系数在多项式环D[x]上的一个形式幂级数.

引理2.2对于整环D上的Fibonacci多项式列{fn}， 有

∈D(x,z)，

∈D(x,z).

证明 利用递推关系fn=xfn-1+fn-2,n≥2以及f0=0，f1=1可得

故

3 有限域上Fibonacci多项式的置换性质

现将Fibonacci多项式看成q元域Fq上的多项式，我们来讨论它们作为有限域Fq上多项式函数的性质，这里p为奇素数，q=pe.

若从Fq到Fq的多项式函数f:cf(c)是Fq的一个置换,则称多项式f∈Fq[x]是Fq上的一个置换多项式.例如，Fibonacci多项式中的f2(x)=x是任何一个有限域Fq上的置换多项式.

引理 3.1[8]多项式f(x)是Fq上的置换多项式的充要条件是

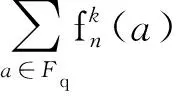
(1)

的值，由此来得到Fibonacci多项式是置换多项式的必要条件.

Fernando和Rashid得出了关于Fibinacci多项式的如下结论.

引理3.2[1](i) 当p≡3(mod 4)且e为奇数时，若n1≡n2(modp2e-1)，则fn1(x)和fn2(x)作为Fpe上的函数相同;

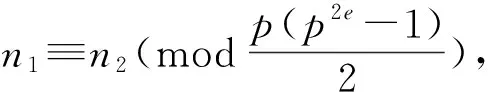
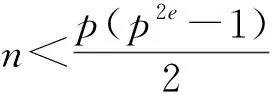
定理3.3设fn为第n个Fibonacci多项式，素数p≡3(mod 4)，e为奇数，q=pe.

(i) 当q=3，即p=3，e=1时，有

(ii) 当q>3时，我们有

其中1≤k≤q2-q+1，

将该式右端按x展开可得

故

(modxq-x)

(2)

当p≡3(mod 4)且e为奇数时，由引理3.2，我们有

故

(3)

由(2)和(3)式可知

(4)

上式关于x∈Fq求和，利用

可得

则有

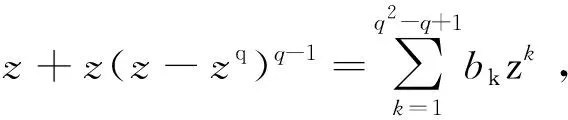
则有

(5)

比较(5)式关于项zi的系数即可得到定理.

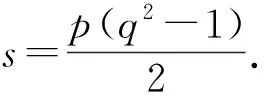
(i) 当q=5，即p=5，e=1时，有

(ii) 当q>5时，有

其中

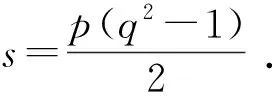
(6)

联立式(2)和(6)有

同样，上式关于x∈Fq求和可得

(modxq-x).

化简上式有

(modxq-x).

从而

(7)

比较式(7)关于项zi的系数即可得到定理.

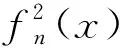
推论3.5设fn为第n个Fibonacci多项式，q=pe.

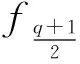
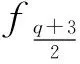
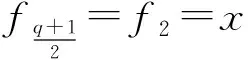
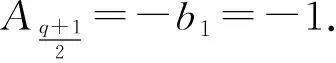
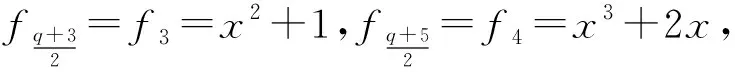
当p≡1(mod 4)，e为任意数，或者p≡3(mod 4)，e为偶数时，若q=5则有b1=1，b2=0，b3=0，b4=0，A4=-b2+b1=1，A5=-(b3+b1)-(A4+A2+A1)=-1-1=-2.由引理3.1知f4和f5在F5上不是置换多项式.当q>5时，同样的有b1=1，b2=0，b3=0，b4=0.根据定理3.4，