盐岩破坏中能量特征应变率效应颗粒流分析

王伟超，朱高房

(河南理工大学 土木工程学院，河南 焦作 454000)

0 引 言

为解决天然气、石油供需矛盾和提高调峰能力，近年来，我国不断加快地下盐岩储库的建设。在建造和运行过程中，由于溶腔速度、形状和所受偏应力及注采速率不同，地下盐岩储库周围盐岩会受到应变率的影响，给地下盐岩储库周围盐岩造成不可逆的损伤，进而影响到地下盐岩储库整体的密闭性和长期稳定性。因此研究不同应变率下盐岩损伤破坏对于地下盐岩储库的建造和安全运行具有重要意义。

在关于岩石应变率效应探索中发现：岩石强度[1]、弹性模量[2-5]、泊松比[6]和破坏形态[7]等宏观力学特性均受到应变速率的影响。在盐岩应变率研究中，梁卫国等[8]认为随着应变率增加，盐岩的泊松比减小且侧向变形能力减弱；LIANG W G等[9]认为盐岩破坏形式不受应变速率影响，且主要破坏形式为脆性断裂并伴有剪切破坏；纪文栋等[10]在进行盐岩三轴压缩应变率效应研究时认为盐岩应变率效应受围压影响较为显著。岩石宏观破坏特征是其内部损伤的外在表现，有的学者除了分析岩石宏观力学特征受应变率的影响外，还借助声发射技术分析岩石损伤演化受应变率的影响[11-13]，姜德义等[14]认为声发射信号频率变化能反映盐岩内部裂纹和损伤演化过程；王伟超等[15]认为应变率和定位点数量呈反比。同时，能量耗散理论的发展也为分析岩石损伤破坏提供新途径，WANG Z L等[16]基于能量耗散理论研究了经过高温处理后的花岗岩能量变化特性；刘新荣等[17]在对比分析Mohr准则和D-P准则后认为基于能量原理强度准则作为盐岩压缩破坏准则具有物理力学意义明确、易使用和应用性强等特点；郭建强等[18]通过定义能量损伤变量方法构建了盐岩损伤演化方程。

综上，总结盐岩的应变率效应研究发现，多数学者在分析盐岩的应变率效应时，更多关注盐岩的宏观力学特征和微观损伤特征，而对于不同应变率下盐岩能量变化特征的研究尚少。本文运用室内单轴压缩试验分析了2×10-3～2×10-5s-1应变速率对盐岩强度和变形的影响，并依据单轴压缩试验获得的宏观力学特征，结合颗粒流程序(PFC-2D)研究应变速率1×10-2～5×10-1s-1内盐岩模型的峰值强度、峰值强度处能量特征和单轴压缩过程中能量特征变化，以期揭示不同应变速率下盐岩损伤中能量变化规律，希望为地下盐岩储库的安全建造和安全运营提供科学指导。

1 室内单轴压缩试验

1.1 试验准备与加载方案设计

试验盐岩来自巴基斯坦深部地下岩层，该盐岩结构致密且纯度高，经分析其可溶NaCl占比达95%以上。参照《煤和岩石物理力学性质测定方法(GB/T23561-2010)》规范，采用干式锯磨法加工试样，见图1，保证加工试件平行度和垂直度均符合规范。测得试样密度和纵波波速参数，具体试样参数见表1。

试验加载设备采用中科院岩土所研发的RMT-150B岩石力学试验系统，并用位移控制方式进行加载，加载过程中实时记录轴向应力-轴向应变之间的关系。根据实际工程需要和参考已有关于盐岩加载应变率的研究，并结合现有加载设备，室内单轴压缩试验采用2×10-5，2×10-4和2×10-3s-13种应变率加载，具体方案见表1。

图1 试件样品

1.2 试验结果

表1给出了试样参数和试验结果。由表1计算应变率2×10-5，2×10-4和2×10-3s-1对应峰值强度的平均值分别为32.01，35.32和37.64 MPa，可以看出，随着应变速率增加，峰值强度平均值随之增大，另外，相同应变速率下盐岩试样峰值强度试验结果表现出了离散性，这是因为天然盐岩在成岩过程中内部会形成一些微节理和微孔隙，由表1中纵波波速也可以推测试样中含有微缺陷，加载过程中这些微缺陷会使试样内部应力场分布产生差异，最终导致试验结果产生偏差。尽管随着应变速率增加，试样的峰值强度平均值有所增加，但由于试验结果离散性较大，并不能确定是由盐岩内部微缺陷导致的，还是由应变率效应引起的。要进一步确定应变速率对盐岩试样力学特征的影响，还需选取更多内部缺陷较少或相近的试件进行分析确定。

表1 试样参数和试验结果

图2给出了不同应变速率下试样应力-应变曲线。尽管盐岩峰值强度、弹性模量和峰值强度处应变均出现较大离散，但由图2可以看出，不同应变速率下盐岩单轴压缩应力-应变曲线走势大致相似，均呈现下凹形趋势，且到峰值强度前均表现为弹塑性变形。与常见岩石不同，该盐岩并未出现明显的压密阶段，由此可以将单轴压缩过程大致分成3个阶段：弹性阶段(oa)、塑性阶段(ab)和破坏阶段(bc)。由图2可以看出，塑性阶段经历了较长时间，表明该盐岩具有较强的塑性变形能力。

图2 不同应变速率下试样应力-应变曲线

2 盐岩单轴压缩颗粒流模拟

2.1 数值模型构建和细观参数标定

基于颗粒流程序(PFC-2D)构建如图3所示尺寸的数值模型，最小颗粒直径为0.4 mm，粒径比为1.625，且服从均匀分布。选用能够同时传递力和力矩的线性平行黏结模型(linear parallel bond model)作为颗粒间接触模型。由于室内试验结果出现了较大的离散性，因此在进行细观参数标定时，分别选取了应变率为2×10-3，2×10-4和2×10-5s-1时试件YB1-4、YB2-4和YB3-1的室内单轴压缩试验结果为参照，利用“试错法”反复标定细观力学参数。采用表2中参数，计算得到盐岩模型的峰值强度、弹性模量等宏观力学特征，与室内试验结果相差较小，对比结果见表3。由表3可知数值模拟宏观力学特征和室内试验吻合度较好。限于篇幅仅给出应变率为2×10-3s-1时试件YB1-4室内试验的应力-应变曲线和破坏形式分别与数值模拟结果的对比，如图4所示。可以看出应力-应变曲线和破坏形式基本吻合，模拟应力-应变曲线并未表现出下凹趋势，可能由于盐岩试件内部存在微节理面，当达到一定应力时，节理面克服摩擦慢慢滑动，此时应力增加速率小于应变增加速率，造成应力-应变下凹，而在进行数值模拟研究时，将岩石材料离散成直径不同的颗粒，并未考虑材料内微节理的存在，因此模拟曲线并未形成下凹趋势。

图3 数值模型

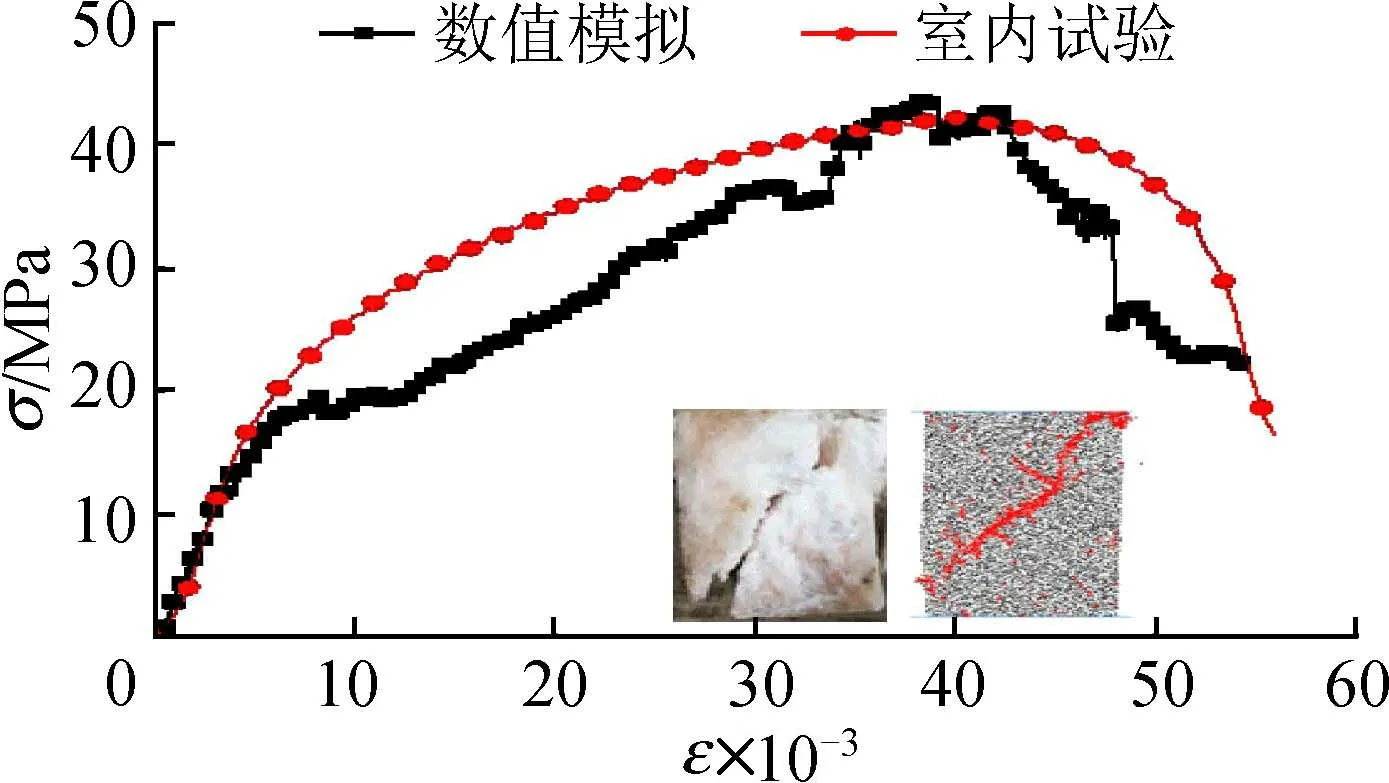
图4 室内试验和数值模拟结果对照

表2 盐岩数值模型细观力学参数

表3 室内试验与数值模拟结果对比

2.2 数值试验加载方案设计

数值模型由四面刚性墙体组成，如图5所示，在进行单轴压缩模拟时，先删除3号和4号两个侧向约束的刚性墙体，然后利用1号和2号墙体作为加载板，通过命令固定底部2号墙体，并且赋予上部1号墙体一定速度。在研究盐岩应变率效应时，保持所标定的盐岩试件细观力学参数不变，然后改变1号墙体加载速率。模拟1×10-2，2×10-2，5×10-2，1×10-1，2×10-1，5×10-1s-16种不同应变速率，当盐岩数值模型应力下降到峰值应力的70%时，终止加载。

图5 数值模型墙体示意图

2.3 应变速率对盐岩模型峰值强度的影响

图6给出了不同应变速率下模型峰值强度。可以看出，盐岩数值模型峰值强度表现出了一定的应变率效应，峰值强度随着应变速率增加而增加。由于应变速率越大，加载过程中模型变形越不充分，从而使模型抵抗外部荷载的能力增强。同时在进行不同应变速率模拟时，通过伺服程序可以使每次试验前的模型内部一致，减小了天然盐岩试样内部微缺陷对试验结果造成的偏差。为进一步研究应变速率和峰值强度之间的关系，对应变速率进行对数运算后，峰值强度和应变速率的对数可近似用一次多项式表达，拟合得到的关系式和R2，如图7所示，可以看出峰值强度和拟合曲线吻合度较好。

图6 不同应变速率下盐岩数值模型峰值强度

2.4 应变速率对盐岩模型损伤中能量特征的影响

2.4.1 岩石损伤能量耗散理论

作用于岩体外力的改变会造成岩体内部损伤、甚至破坏，同时伴随着能量交换。为进一步分析岩体损伤破坏过程中能量交换，取单位岩体进行分析，由于该过程中热交换极少，因此可以忽略，根据热力学第一定律，受外力作用单位岩体产生变形，则外力对单位岩体做的功即为总输入能量U，则可得

图7 峰值强度拟合曲线

U=Ue+Ud，

(1)

式中：Ue为单位岩体可释放弹性应变能；Ud为单位岩体耗散应变能。

图8给出了应力-应变曲线中单位岩体的可释放弹性应变能Ue(阴影面积)和耗散应变能Ud之间的关系，其中Eu为卸载模量。

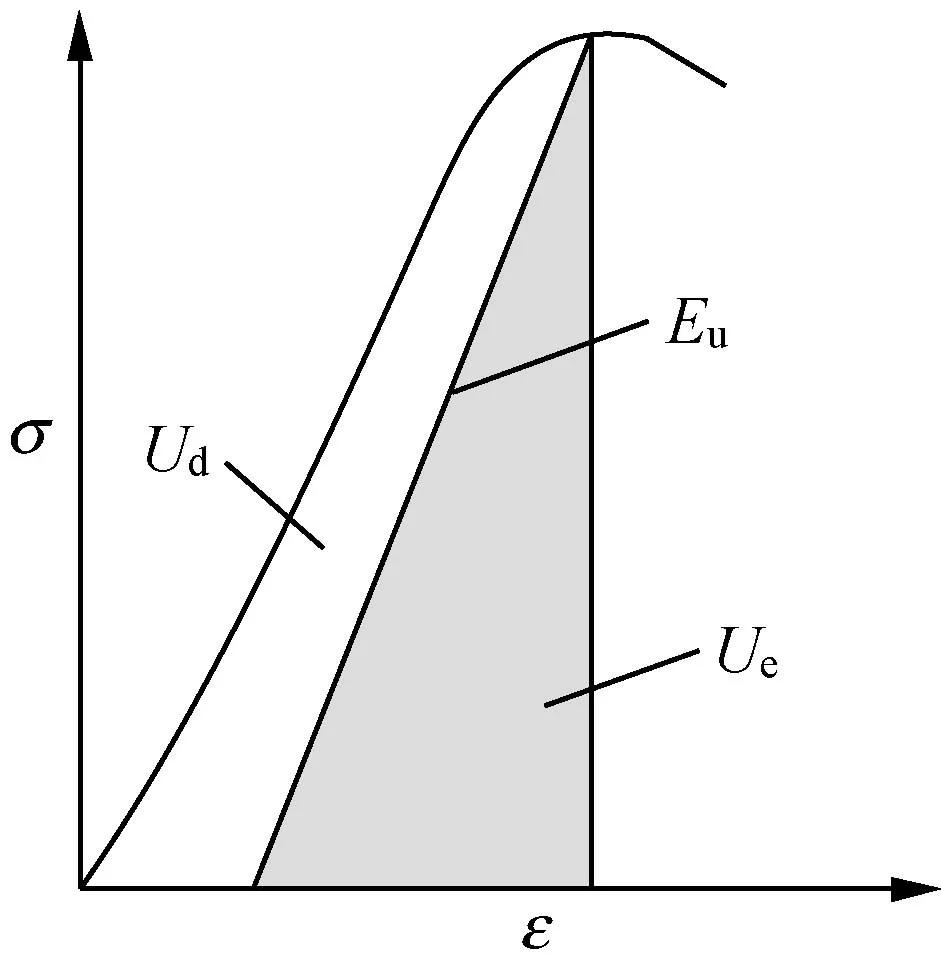
图8 单位岩体中能量关系曲线

在单轴压缩过程中，单位岩体的U，Ue和Ud计算公式可以改写为

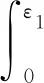
(2)

(3)

(4)

式中：σ1为轴向应力；ε1为轴向应变；在进行可释放弹性应变能时，为简化计算卸载模量Eu，可用弹性模量E0代替[16]。

2.4.2 应变速率对盐岩模型峰值强度处能量特征的影响

表4给出了不同应变速率下盐岩模型单轴压缩试验峰值强度处的U，Ue，Ud和Ue/U。由表4可知，盐岩模型单轴压缩峰值强度处的U、Ue和Ud均随着应变速率的增加而增加。

表4 不同应变速率下盐岩峰值强度处应变能

峰值强度处Ue随着应变速率增加而增大，根据计算公式和模型峰值强度随应变速率变化规律，可推断出峰值强度处Ue会随应变速率增加而增加；Ud随应变速率增加而增加，原因为：一是加载应变速率越快，盐岩模型内部损伤程度越大，产生的细小微裂纹越多，当达到峰值强度时，裂纹扩展所耗散的能量越多；二是加载应变速率的增加导致单个裂纹发育扩展不充分，因此，当达到峰值强度时，单个裂纹进行延伸扩展时所需要的能量也越多。为了进一步分析峰值强度处U、Ue和Ud分别与加载应变率的关系，将应变速率取对数，并建立半对数坐标系，然后进行曲线拟合，结果如图9所示，可看出U和Ud分别与应变速率的对数之间呈二次函数关系，而Ue与应变速率的对数可用一次多项式表示。

由表4可看出，盐岩模型峰值强度处Ue/U取0.18～0.21，其结果不受应变速率影响，但在单轴压缩模拟试验过程中，盐岩变形和内部损伤破坏消耗了大部分的外力做功，仅有小部分的功会转化成可释放的弹性应变能，这与大理岩、花岗岩等脆性岩石相反，脆性岩石变形量和内部损伤较小，导致大部分外力功转化成可释放弹性应变能，因此在单轴压缩中会出现片帮飞溅现象，而盐岩不会出现类似现象。

2.4.3 盐岩模型单轴压缩过程中能量特征变化

岩石损伤破坏过程中伴随着能量转化，为了研究盐岩单轴压缩过程中能量转化，分别绘制了不同速率下盐岩模型单轴压缩过程中U，Ue和Ud随轴向应变的变化曲线关系，见图10。

由图10(a)～(f)可以看出，不同应变速率下的弹性阶段U大部分转化成Ue，且二者略有增加；塑性阶段U和Ud均快速增加，而Ue缓慢增加；破坏阶段U和Ud持续增加，而Ue降低，即不同应变率下盐岩模型在相同压缩阶段能量特征变化基本相同，且U,Ue，Ud分别与轴向应变的变化趋势大致相近，能量随轴向应变整体变化趋势受应变速率的影响较小。这是因为数值模型不同于天然盐岩，天然盐岩在成岩过程中内部所含的微节理、微孔隙和其他矿物杂质等缺陷会使盐岩试样在受力时内部应力场的分布产生差异，进而会影响其力学特征和能量演化特征，试验前可利用伺服程序使试验模型保持高度一致，尽量减少由于模型内部差异带来的试验偏差。

图9 盐岩峰值强度处对应的应变能与应变速率的对数关系

观察同一应变速率下不同压缩阶段，图10(a)显示盐岩模型压缩过程中在弹性阶段，U，Ue和Ud三者曲线整体呈现重合形态，U和Ue重合度很高，而Ud却很小，塑性阶段U和Ud快速大幅增加，Ue有所增加但增幅较小，进入破坏阶段U和Ud不断持续增加，但Ue却出现降低，因此，同一应变速率下盐岩模型在不同压缩阶段能量特征变化趋势不同，这是因为不同压缩阶段模型内部颗粒受力产生了位错和黏结接触变化。为进一步分析能量特征变化趋势的不同，绘制了应变速率为1×10-2s-1时不同压缩阶段下Ue/U随应变变化趋势图，如图11所示。盐岩在压缩弹性阶段，颗粒之间的接触力小于黏结强度，模型内部只产生极少的裂纹，所以大部分外力做功转化成Ue，且Ud很小，由图11可以看出弹性阶段70%以上的外力做功转化成Ue储存于模型内部，但由于弹性阶段变形较小，因此弹性阶段U较小，所以三条曲线看上去呈重合形态。

在压缩塑性阶段，随着外力不断压缩，持续对模型做功，U不断增加，此阶段模型的变形不断增加，内部颗粒产生位错和移动，由于颗粒间的位错和移动消耗了很多能量，颗粒之间接触力不断增大，当颗粒间接触力大于黏结强度时，黏结接触失效，从而形成微裂纹，同样黏结接触失效也会消耗能量，此阶段Ud快速增加，由图10(a)可以明显看出Ud的增加趋势大于Ue，表明塑性阶段模型的变形和裂纹的产生占据了主导地位。

当应力达到峰值强度时，模型进入破坏阶段，与脆性岩石不同，盐岩在破坏阶段仍具有一定的承载能力，因此U也在不断增加，其增加速率略有减小；此时模型内有大量颗粒间的黏结接触失效，产生更多裂纹，裂纹不断生成、扩展和汇集形成主破坏界面，持续压缩模型，主破坏界面产生滑移，所以此阶段Ud不断增加；压缩过程中横向变形和体积应变不断增大，模型内部少量颗粒周围约束减少，颗粒位置不断调整，由于物质内储存的能量越低，物质状态越稳定，所以储存于颗粒间接触键的弹性应变能释放，模型内的Ue降低。

3 结 论

(1)不同应变速率下盐岩单轴压缩应力-应变曲线变化趋势大致相似，达到峰值强度前均表现出弹塑性变形特征，且其压缩过程均经历弹性、塑性和破坏3个阶段。随着应变速率增加，盐岩模型峰值强度逐渐增大。

(2)盐岩模型峰值强度处对应的U、Ue和Ud随着应变速率的增加而增加。在半对数坐标系中，盐岩模型峰值强度处总输入能量和耗散应变能分别与应变速率的对数之间呈二次函数关系，而可释放弹性应变能与应变速率的对数呈一次函数关系。

(3)不同应变率下盐岩模型在相同压缩阶段能量特征变化基本相同，且U，Ud，Ue分别与轴向应变的变化曲线走势大致相同，能量随轴向应变整体变化趋势受应变速率的影响较小。同一应变速率下，不同单轴压缩阶段盐岩模型能量特征变化趋势不同，弹性阶段大部分外力做功转化成可释放应变能；塑性阶段耗散应变能快速大幅增加；破坏阶段耗散应变能持续增加，弹性应变能则出现降低。

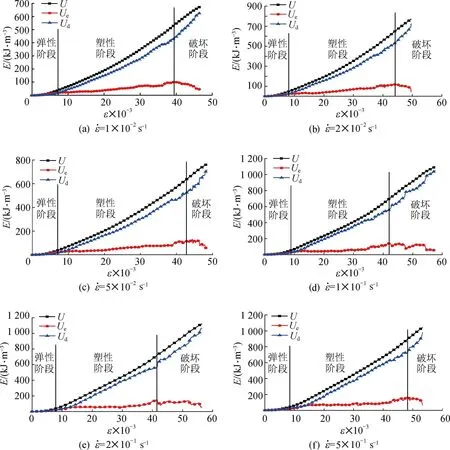
图10 不同应变速率下盐岩单轴压缩能量变化过程

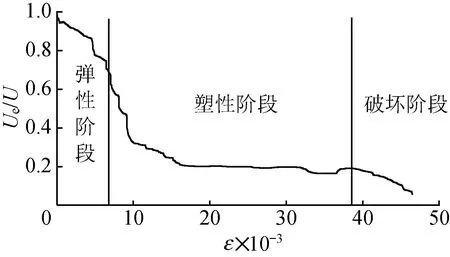
图11 不同压缩阶段下Ue/U 变化趋势