简易逻辑、计数原理、算法语言、二项式定理、复数、概率统计测试题B

■湖北省巴东县第三高级中学 贺显孟

一、选择题

1.（2020年吉林省长春市模拟）已知复数z=1+i，则下列命题中正确的是（ ）。

A.1 B.2 C.3 D.4

2.变量X与Y相对应的一组数据为（10，1），（11.3，2），（11.8，3），（12.5，4），（13，5）；变量U与V相对应的一组数据为（10，5），（11.3，4），（11.8，3），（12.5，2），（13，1）。r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则（ ）。

A.r2＜r1＜0 B.0＜r2＜r1

C.r2＜0＜r1D.r2=r1

3.（2020年宁夏石嘴山市第三中学检测）若命题“∃x∈R，使x2+（a-1）x+1＜0”是假命题，则实数a的取值范围为（ ）。

A.1≤a≤3 B.-1≤a≤3

C.-3≤a≤3 D.-1≤a≤1

4.（2020年吉林省梅河口市第五中学检测）已知复数z=a+2i-i（a-i）在复平面内对应的点在第四象限，则实数a的最小正整数值为（ ）。

A.1 B.2 C.3 D.4

5.（2020年上海市曹杨二中月考）已知a，b为实数，则2a＞2b是log2a＞log2b的（ ）。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

6.（2020年江西省6月联考）已知（a+b）2n展开式的第4项与第8项的二项式系数相等，则（2x-1）n展开式中x3的系数为（ ）。

A.80 B.40 C.-40 D.-80

7.（2020年吉林省示范高中模拟）执行如图1所示的程序框图，若x∈R，则输出y的最小值是（ ）。

图1

A.20 B.19 C.10 D.9

9.（2020 年 名师联盟高三5月联考）某程序框图如图2所示，其中g（n）若输出则判断框内可以填入的条件为（ ）。

A.n≥2020？

B.n＞2020？

C.n≤2020？

D.n＜2020？

10.某市委从组织机关10名科员中选3人担任驻村第一书记，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为（ ）。

A.85 B.56 C.49 D.28

11.（2019年惠州市第二次调研）旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若不能最先去甲景区旅游，不能最后去乙景区和丁景区旅游，则小明可选的旅游路线数为（ ）。

图2

A.24 B.18 C.16 D.10

12.（2020年山西省祁县中学检测）下列说法正确的是（ ）。

A.“f（0）=0”是“函数f（x）是奇函数”的充要条件

B.若p：∃x0∈R，-x0-2021＞0，则¬p：∀x∈R，x2-x-2021＜0

D.若p∧q为假命题，则p，q均为假命题

13.盒中有10个螺丝钉，其中有3个是坏的，现从盒中随机地抽取4个，那么概率是的事件为（ ）。

A.恰有1个是坏的

B.4个全是好的

C.恰有2个是好的

D.至多有2个是坏的

14.（2020年福建省上杭一中检测）随机变量ξ服从二项分布ξ～B（n，p），且E（ξ）=300，D（ξ）=200，则p等于（ ）。

15.（2020年福建省莆田市第一中学检测）设随机变量ξ的概率分布列如表1所示，则P（|ξ-3|=1）=（ ）。

表1

二、填空题

16.（2020年河北省张家口市模拟）若复数z满足z（2-i）=18+11i，则|-4i|=____。

17.甲、乙、丙3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是____。（用数字作答）

18.设随机变量X的概率分布列如表2所示：

表2

若F（x）=P（X≤x），则当x的取值范围是[1，2）时，F（x）等于____。

19.已知随机变量ξ服从正态分布N（2，σ2），且P（ξ＜4）=0.8，则P（0＜ξ＜4）=____。

21.（2020年河北省张家口市联考）在10个排球中有6个正品，4个次品。从中抽取4个，则正品数比次品数少的概率为____。

22.（2020年吉林省梅河口市第五中学检测）已知p：直线与圆O：x2+y2=1有交点；q：A，B为△ABC的内角，若sin2A=sin2B，则三角形为等腰三角形。若p或q为真，则实数k的取值范围是____。

三、解答题

24.（2020年安徽省宣城市八校联考）已知p：关于x的方程x2+（a-2）x+4=0无解，q：2-m＜a＜2+m（m＞0）。

（1）若m=5时，“p∨q”为真命题，“p∧q”为假命题，求实数a的取值范围。

（2）当命题“若p，则q”为真命题，“若q，则p”为假命题时，求实数m的取值范围。

25.已知10件不同的产品中有4件是次品，现对它们进行测试，直至找出所有的次品为止。

（1）若恰在第5次测试才测试到第1件次品，第10次才找到最后一件次品，则这样的不同测试方法数是多少？

（2）若恰在第5次测试后就找出了所有次品，则这样的不同测试方法数是多少？

26.在某校教师趣味投篮比赛中，比赛规则是：每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖。已知教师甲投进每个球的概率都是。

（1）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望。

（2）求教师甲在一场比赛中获奖的概率。

27.（2020年内蒙古鄂尔多斯市第一中学模拟）“微信运动”是手机APP推出的多款健康运动软件中的一款，某学校140名老师均在微信好友群中参与了“微信运动”，对运动10000步或以上的老师授予“运动达人”称号，低于10000步称为“参与者”，为了解老师们的运动情况，选取了老师们在4月28日的运动数据进行分析，统计结果如表3：

表3

（1）根据上表说明，能否在犯错误的概率不超过0.05的前提下认为获得“运动达人”称号与性别有关？

（2）从具有“运动达人”称号的教师中，采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动，若从选取的10人中随机抽取3人作为代表参加开幕式，设抽取的3人中女教师人数为X，写出X的分布列并求出数学期望E（X）。

参 考 公 式：K2=其中n=a+b

参考数据：

表4

28.（2020年吉林省示范高中模拟）搪瓷是在金属坯体表面涂搪瓷釉而得到的制品。曾经是人们不可或缺的生活必备品，厨房用具中的锅碗瓢盆，喝茶用到的杯子，洗脸用到的脸盆，婚嫁礼品等，它浓缩了上世纪整整一个时代的记忆。某搪瓷设计公司新开发了一种新型复古搪瓷水杯，将其细分成6个等级，等级系数X依次为3，4，5，6，7，8，该公司交给生产水平不同的A和B两个厂生产，已知A厂生产的该种搪瓷水杯的等级系数X服从正态分布N（μ，0.25），且在电商平台上，A厂生产的搪瓷水杯的零售价为36元/件，B厂生产的搪瓷水杯的零售价为30元/件。

（1）①求A厂生产的搪瓷水杯的等级系数的平均值；

②若A厂生产了10000件这种搪瓷水杯，记Y表示这10000件搪瓷水杯等级系数X位于区间（5.5，6.5）内的产品件数，求E（Y）。

（2）从B厂生产的搪瓷水杯中随机抽取30件，相应的等级系数组成一个样本，数据如图3所示：

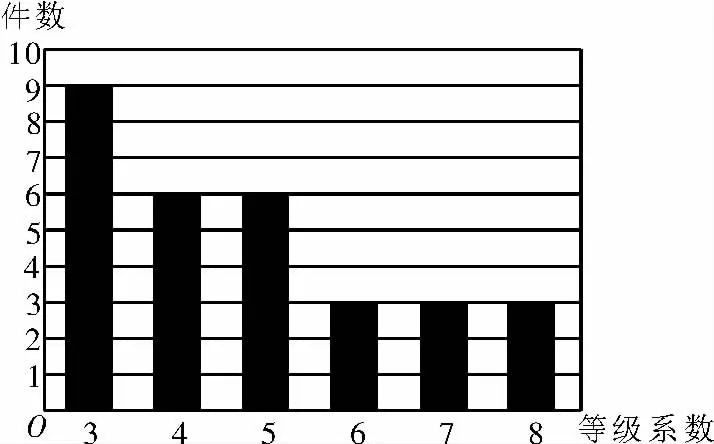
图3

注：若Z～N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974。