联合手肘法和期望最大化的高斯混合聚类电力系统客户分群算法

陈 聿，田博今，彭云竹，廖 勇

（1.重庆广汇供电服务有限责任公司信息通信分公司，重庆 400014；2.国网重庆市电力公司信息通信分公司，重庆 401120；3.重庆大学微电子与通信工程学院，重庆 400044）

（∗通信作者电子邮箱liaoy@cqu.edu.cn）

0 引言

电力系统客户行为分析是指分析用电数据之间的关系和相似性，找出客户潜在的行为习惯，并对客户进行细分，对指导客户的用电行为和节能改造具有重要意义。电力系统客户数据具有噪声大、异常点多、密度不均匀和数据较分散的特点。现有的客户划分方法是粗放式的，只使用单一的特征属性对客户进行细分。随着产品服务和客户需求的多样化，单一特征属性的划分方法表现出了很多不足和缺陷。

数据聚类作为数据挖掘的关键和核心处理，代表性聚类算法包括K-Means 聚类［1］、模糊C 均值聚类［2］、核密度聚类及构建有限混合模型聚类等。近年来，高斯混合模型（Gaussian Mixture Model，GMM）聚类算法发展非常迅猛，然而它的缺陷也非常明显，在聚类之前，需要提前确定最终的聚类数目。很多研究人员对其进行改进，并给出了新型的GMM 算法。文献［3］提出一种基于GMM 与K-Means 的改进聚类方法，该方法在K-Means 聚类步骤中经由合并操作自动测定聚类数目，并为后续的GMM 聚类步骤提供初始聚类中心。在有限混合模型分类阶段，基于像素分布，利用期望最大化（Expectation-Maximization，EM）算法估计类别似然，采用最大似然分类技术估计每个像素的最终类别，该方法可得到更高的分类精度，但实现过程较为复杂。Song 等［4］提出了一种基于GMM 概率密度的数据流聚类方法，该方法仅仅将标准EM 算法应用于新到达的数据而不是将整个历史数据保存在内存中，该方法的可行性得到验证，但聚类对应的个数是不确定的，并且此算法聚类运行时间长。

另一方面，目前，常用的确定最佳聚类数目的算法包括手肘法和轮廓系数法，然而，由于轮廓系数法的复杂度较高，本文采用手肘法。科研人员对基于误差平方和（Sum of the Squared Errors，SSE）的手肘聚类方法进行分析与探究。Syakur等［5］提出结合K-Means方法和手肘法，从而提高了数据处理的效率，并能有效提升K-Means 的性能，改进后的算法在聚类上有一定的效果。文献［6］提出根据手肘法关系图，求出图中误差平方和的最大差值的方法，利用数据集预抽样并且将程序部署在Spark 平台之上的方式自动获取手肘法的肘点k 值，根据此方法自动获取K-Means 最优k 值。上述方法可准确得到聚类个数，但聚类结果在聚类紧凑度、分离度和复杂度上都还需要进一步的改善。

为进一步提升电力系统客户的用户体验，针对现有聚类算法对该类数据寻优能力差、紧凑性不足，较难求解聚类数目最优值的问题，本文提出联合手肘法和期望最大化（EM）算法的GMM 聚类算法，简称SEG（SSE-EM-GMM）算法。该算法主要分为两个步骤：1）根据手肘法对所得数据进行第一次聚类，绘制出SSE 与k 值的关系折线图，并确定最优k 值；2）由得到的k值来随机选取聚类中心，利用EM 算法进行GMM 聚类，实现对数据的合理聚类分析。将本文方法用于对电力公司的客户数据分析，聚类得到电力公司客户分群，并通过内部评价指标、外部评价指标及全局评价指标该算法与其他算法进行对比，验证了所提算法的可行性和有效性。

1 SEG算法

SEG 算法首先寻求合适的聚类数目k 使后面的聚类算法达到最优，然后使用基于EM 的GMM 聚类算法对电力公司的客户信息进行聚类。

1.1 高斯混合模型

高斯混合聚类采用概率模型表达聚类原型。假定数据符合高斯混合分布［7］：

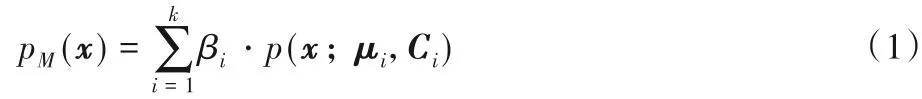
其中：βi为第i 个分模型生成的概率，且将数据分为k 类；p(x；μi，Ci)为多维高斯分布概率密度函数，定义如式（2）所示：

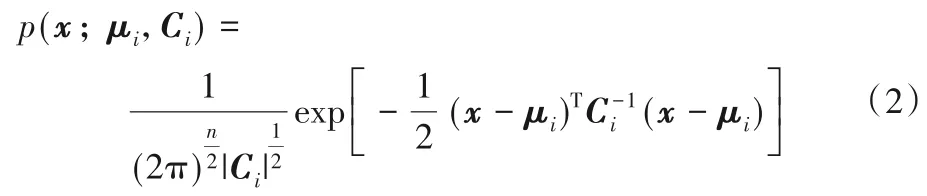
其中：x为n维随机变量，定义为x=[x1，x2，…，xn]T，Ci为协方差矩阵，μi为均值向量。从式（2）可以看出，多维高斯分布完全由协方差矩阵和均值向量确定。由中心极限定理可知，当k和样本足够多时，每一块区域都能用高斯分布来描述。

为了便于分析，将p(x；μi，Ci)记为p(x|μi，Ci)，引入隐变量p(zj=i)，其含义为第i个分模型生成的概率，即为βi。样本xj为第i 个分模型生成的后验概率为pM(zj=i|xj)，根据贝叶斯公式，得到式（3）的结果：

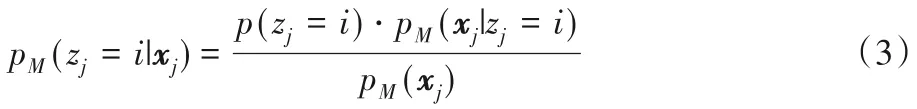
式中pM(xj|zj=i)为第i个分模型生成xj的先验概率，完全由Ci和μi决定，即为：

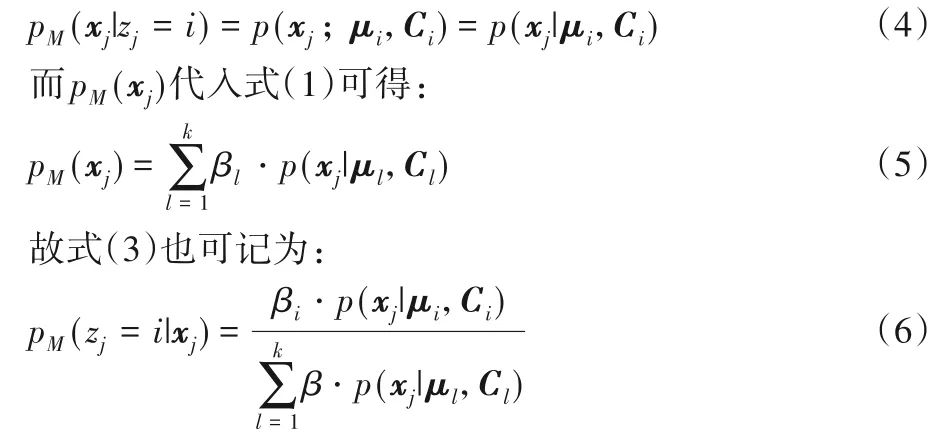
其中：pM(zj=i|xj)，i=1，2，…，k。当式（1）的参数已知时，将数据集划分为k类，每个样本xj的分类ξj由式（7）决定：

而目前的问题在于式（1）中的参数是未知的，故需要通过数据集作参数估计。常采用最大似然估计法，即将m 个样本作为独立事件，其概率为：

将式（8）取对数，有：

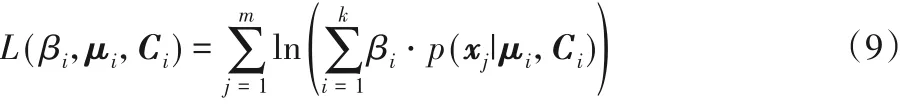
最大似然估计需要知道每一个样本的具体分布，而由于存在隐变量βi，即获得样本xj时并不知道它的来源分布，故无法简单地对参数求偏导估计未知参数，需要采用EM算法。

EM 算法的核心思想是不断迭代提高精度［8］。为了使L(βi，μi，Ci)最大化，需要对3 个参数求偏导。首先求解βi，由于βi还有存在约束，故问题转化为：

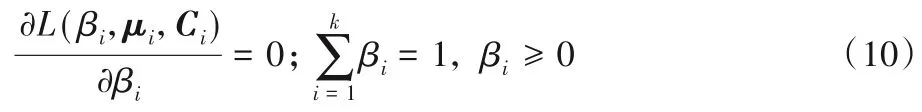
求解以上条件极值问题，采用拉格朗日乘数法求解［9］，引入乘子λ，式（10）转换等式（11）：

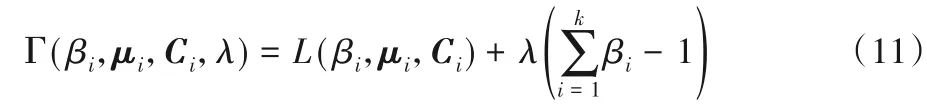
将式（11）对βi求偏导并令其为0，得到：

其次求解μi，式（9）对μi求偏导，得到式（13）：

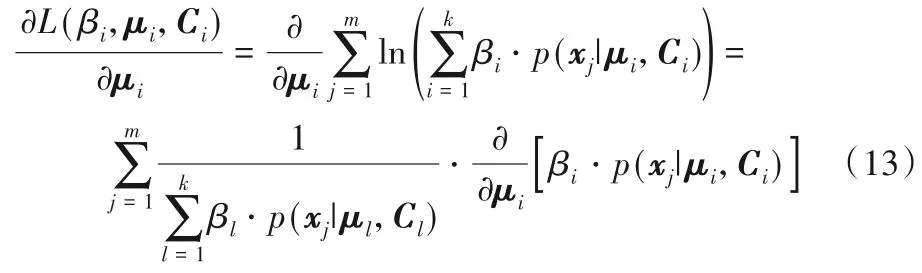
式（13）的右端末项如式（14）所示：

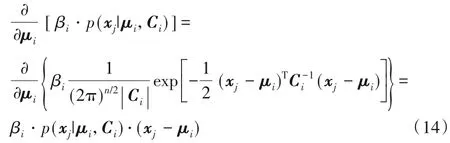
代入原式（13），令其为0，有：

最后求解Ci，同样地，式（9）对Ci求偏导，得到等式（16），等式右端末项如式（17）所示：

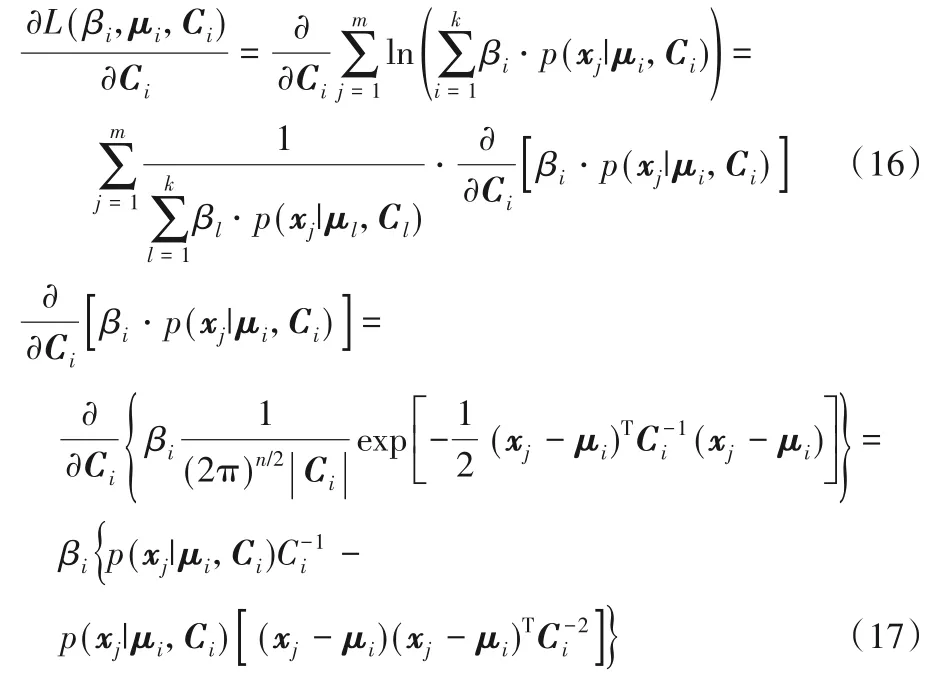
将式（17）代入式（16），令其为0，有：

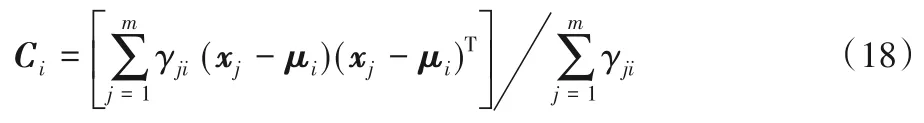
上述推导过程得出了参数与后验概率之间的迭代关系，如图1所示。

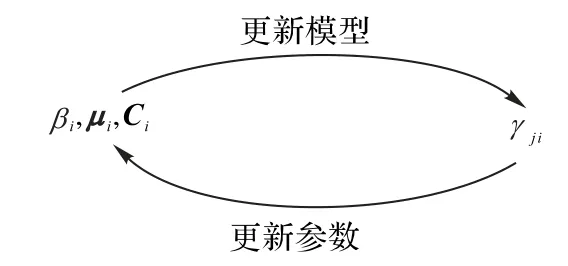
图1 参数与后验概率关系Fig.1 Relation between parameter and posterior probability

每一次迭代更新βi，μi，Ci与γji，增加迭代的次数可以提高精度，当似然函数L(βi，μi，Ci)增长较少时即可停止迭代。高斯混合模型聚类如算法1所示。

算法1 高斯混合聚类。

1.2 联合手肘法和EM的高斯混合聚类算法

本文采用基于SSE 的手肘法确定聚类数目，其中误差平方和（SSE）的定义如下：

其中：p 表示第i 个类组θi中的数据对象，qi表示第i 类组中所有数据对象的均值，k 表示分类簇的数量。联合手肘法和EM的高斯混合聚类如算法2所示。

算法2 联合手肘法和EM的高斯混合聚类算法。

2 聚类有效性评价

聚类质量评价指标有很多种，在本文中本文选择了三类常用的评价指标作为本文聚类结果的评价指标。本文选取了紧凑度（Compactness Index，CI）［10］作为内部评价指标，FM（Fowlkes-Mallows）［11-12］和Adjusted-Rand（AR）［13］作为了外部评价指标，以及分离度（Degree of Separation，DS）［14］作为了全局评价指标。

2.1 内部评价指标

CI 指标 用于形容簇内数据集的集中程度，簇内的数据越相似，它的紧凑度就会越高，就说明聚类效果更好［15］。

总体簇内紧凑度的计算方法如式（20）所示，其中n 代表聚类的样本数，每个样本是p 维的行向量X={x1，x2，…，xn}，X ⊂Rp，c 代表聚簇的数量；U 为c × n 矩阵，样本属于模糊子集的隶属程度；uij为数据j对第i类的支持度，其值越大就说明它的信息量越大；V 为c × p 矩阵，表示聚类原型；距离采用欧氏距离。

CI 值可以增大指标的敏感度，使得有效性指标能够正确地判断出小类的存在，进而判断出最佳聚类数。总体紧凑值越小，代表簇越紧凑。

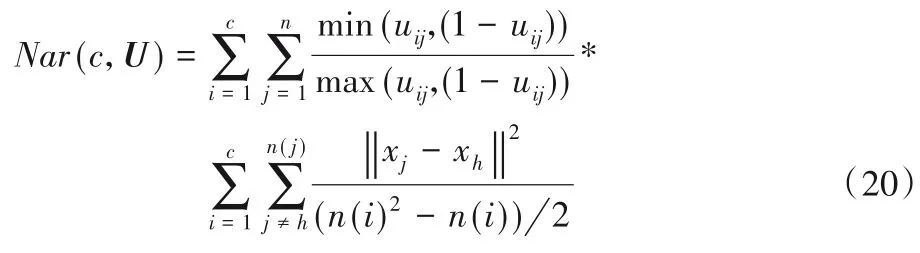
2.2 外部评价指标

1）FM指标。

典型的外部聚类评价指标有FM 指标和AR 指标等［16］，它们都是用于测试聚类结果准确性的经典指标。

FM指标的计算方法如式（21）所示：

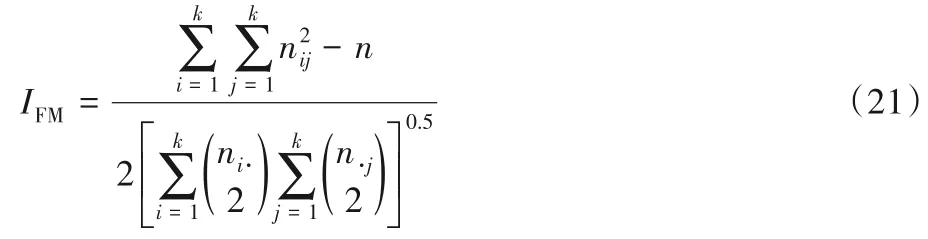
FM 指标的值介于0～1，其值越大，代表聚类划分后的簇与标准簇就越接近，当且仅当聚类结果与标准簇完全一致时，IFM=1。

2）AR指标。

本文另设相关参数如下公式所示：

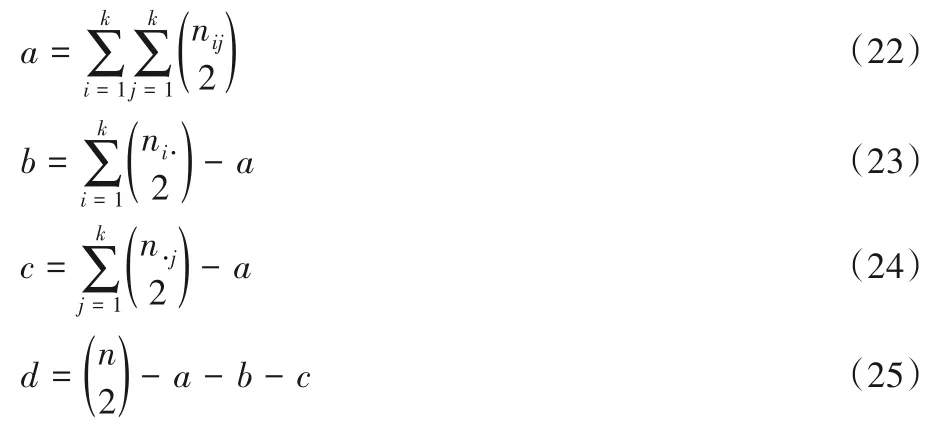
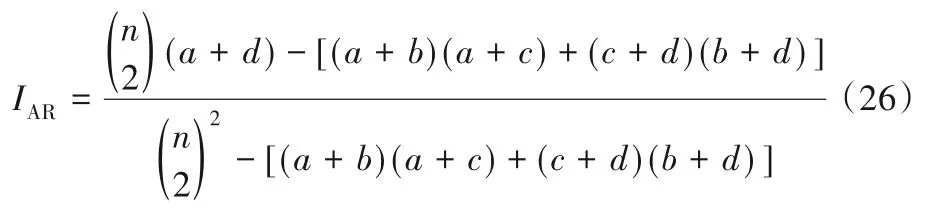
AR 指标值的范围也是0～1，并且值越大，越接近于1，就代表划分结果越好。

2.3 全局评价指标

分离度（DS） 分离度表示各个簇之间的分离程度，簇与簇之间分离越清晰，分离度就会越高［17］。

簇间分离度公式如式（27）和式（28）所示：

将所有子簇的分离度相加得到总体分离度，其计算方法如式（29）所示：

其中：Fij表示模糊偏差；α 表示惩罚系数，其默认取值为0.5，使用模糊偏差来放大隶属度矩阵的特征。两个簇的模糊偏差相乘就表示两个模糊集合的分离度，簇间分离越清晰，分离度就越高，该值就越小。

3 应用案例

3.1 数据处理

数据预处理，即统一和规范各种数据，以便这些数据可以直接用于以后的聚类。

1）数据准备。

数据准备即获取客户信息，根据变量对聚类结果的影响大小选取合适的特征作为聚类分析的主要对象，作为聚类分析的数据基础。

特征属性的选取 通过对电力通信客户服务中客户行为的内容和属性的调查研究，建立了反映客户行为规律分析、客户使用行为分析和客户群细分的指标体系，使管理者能够优化业务组织，改进服务模式。如表1 所示，本文基于聚类的客户细分的分群指标数据可分为四部分：一是客户消费水平，该部分指标集中反映的是客户的消费水平；二是客户掉电敏感程度，该部分指标反映的是客户对于用电需求的紧急程度；三是客户欠费风险，该部分反映的是客户在缴费方面的一个诚信度；四是客户设备风险情况，该部分指标集中反映的是客户安全用电的意识。通过这四个部分的指标分析，可以较为全面地分析电力公司信通客户的行为规律。

表1 客户分群评估因素Tab.1 Customer segmentation assessment factors

数据采集 根据整理出的客户分群评估因素调取了10 000名客户的相应数据，表2显示的是部分客户的消费水平信息。

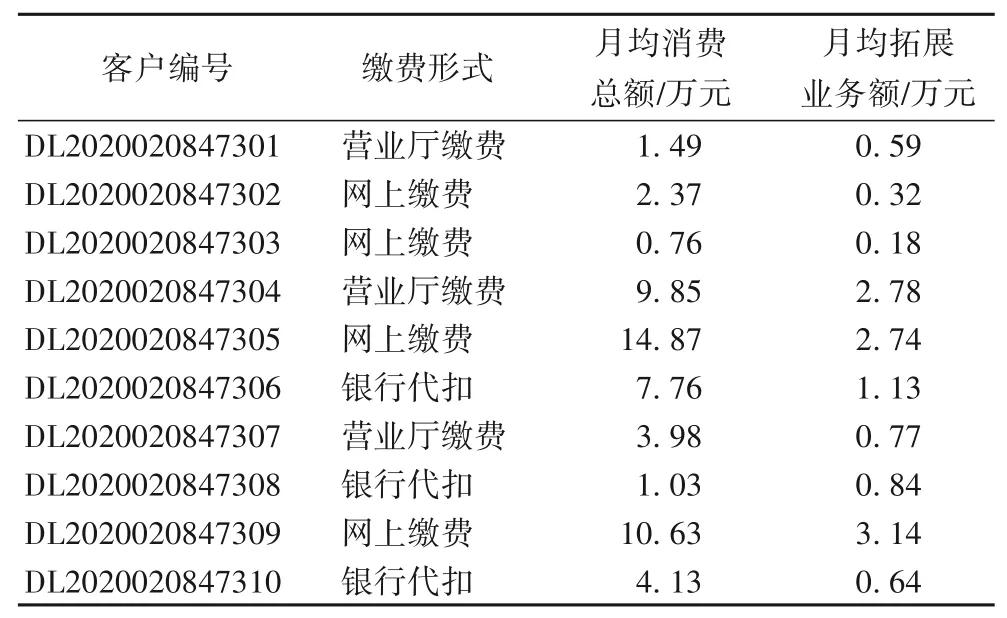
表2 客户消费水平信息Tab.2 Customer consumption level information

客户掉电敏感程度信息主要包含了用电类型、掉电后投诉次数和合同容量等内容，部分详细数据见表3。

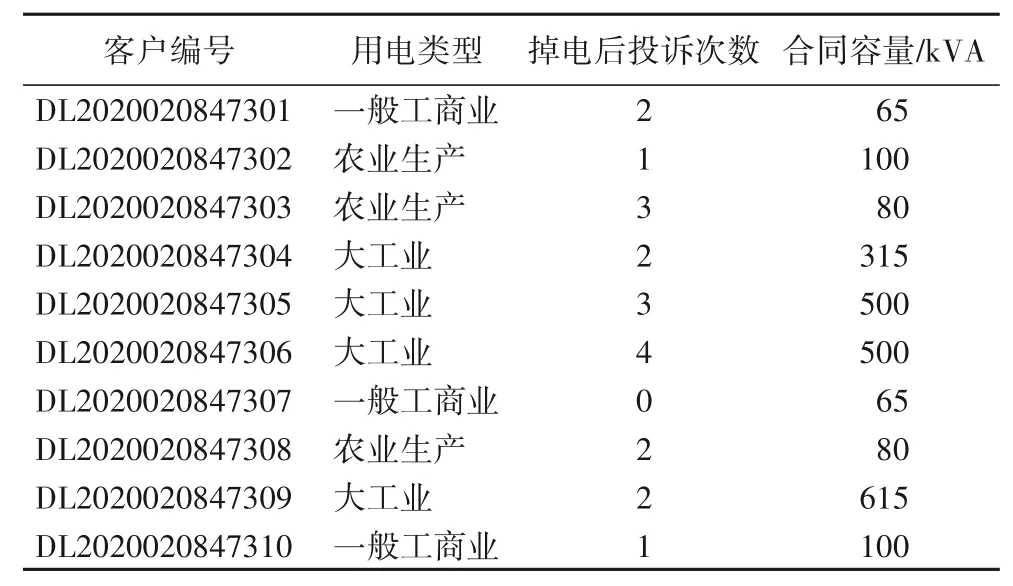
表3 客户掉电敏感程度信息Tab.3 Customer power loss sensitivity information

客户欠费风险信息部分采集数据详见表4。表中所列的几项指标可以比较准确地反映客户的缴费及时性。

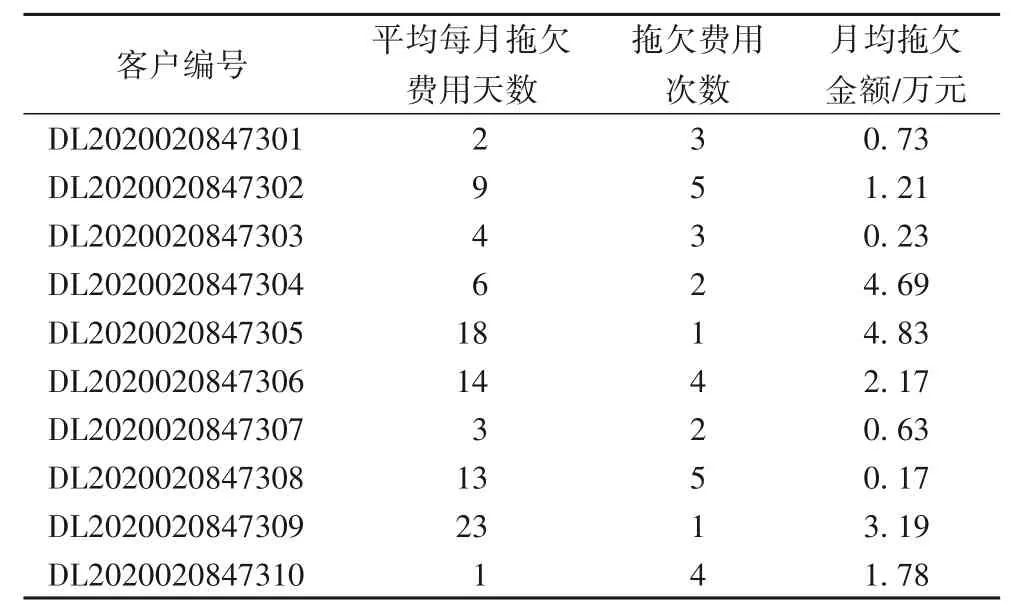
表4 客户欠费风险信息Tab.4 Customer arrears risk information

表5 展示的是部分客户的客户盗电风险各项指标的数据。其中实际用电与合同用电量的匹配度计算公式如下所示：

其中：λ表示匹配度，s表示实际用电量，r表示合同用电量。

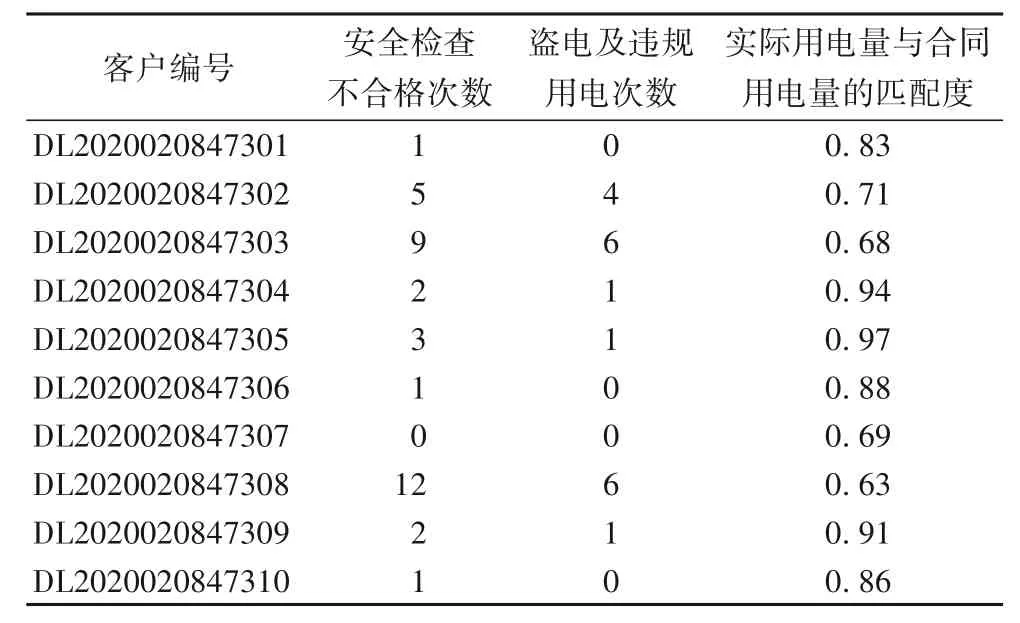
表5 客户盗电风险信息Tab.5 Customer electricity stealing risk information

2）数据预处理。

主要包括数据清洗以及数据转换。

①数据清洗。

为了提高数据完整性并标准化数据表单，需要进行以下处理。

a）空缺值处理。

在收集的10 000名客户的数据信息中存在很多的不完整的信息。例如有的客户的月均消费总额为空，为了保证聚类结果的准确性，本文采用均值内插的方法来填充缺失数据，具体做法是使用该属性的众数来插补缺失的值填上残缺的数据，并删除属性数据缺失量大于两条的信息。

b）噪声数据处理。

在许多数据中，会出现与事实不符、超出正常的范围的异常数据，本文通过箱型图分析来对采集的数据自动进行异常数据识别。具体做法是：首先本文定义上四分位U 和下四分位L，U取值表示该属性的所有样本中只有四分之一的数值大于它，L 取值表示该属性的所有样本中只有四分之一的数值小于它；其次，本文设定上四分位与下四分位的插值为IQR，即IQR=U -L；那么，上界Uk=U+1.5IQR，下界Lk=L -1.5IQR；最后，该属性的所有数据中超过上界Uk和下界Lk的数据都被判断为异常数据，最后将这些异常数据所在的整条信息删除。

c）不一致数据处理。

在众多的数据当中也不乏有少数与数据格式不相符的数据，比如在缴费形式那里填写的是用电类型，在掉电后投诉次数那里填写合同容量，这样的不一致数据相对比较少，对于这样的数据本文采用中值插补的方法来替换数据，具体做法是使用该属性中所有值的中位数来替换这些数据。

②数据转换。

经过清洗后的数据虽然已经确保了信息的完整度以及准确性，但要想使用本文的机器算法来对这些信息进行处理，还需要把形式各异的数据转化为统一的数据形式并进行标准化处理。在采集的数据信息中本文发现不同的指标有着不同的数据格式，并且数据的取值范围各不相同。通过不同的数学统计方式来寻找到衍生字段，实现数据形式的统一；将每一个变量与该变量均值的差除以该变量的标准差得到标准化后的数据；研究使用需求相关的各类特征变量在实际应用中的影响程度，根据影响因子ui（i=1，2，…，n）的大小为其输入设置不同的比重，其中n 代表属性的个数。具体做法是：一个属性对应一个影响因子ui，每个属性对应的比重Pi，其计算公式如下所示：

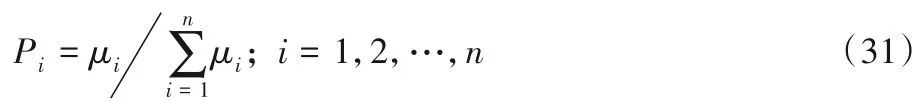
通过这一系列的数据处理和转换就得到了本文最终聚类处理所需要的数据。

3.2 结果分析与评价

本文将所提方法用于测试电力公司提供的信通客户数据，并通过和K-Means 以及层次聚类的测试结果指标进行对比来对本文所提方法的聚类结果进行综合评价分析。

1）聚类结果。

为得到比较好的聚类效果，在选取影响聚类结果的一些特征变量后，本文采集10 000名客户的信息，并将这些数据信息进行数据清洗和数据转换，然后使用了本文的SEG 聚类算法进行了数据分析，首先使用手肘法确定最佳k 值，仿真的结果如图2所示。

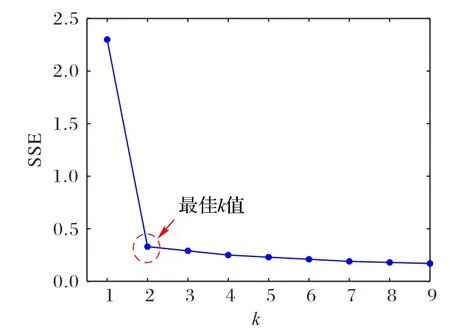
图2 手肘法确定k值Fig.2 k value determined by elbow method

由图2 可以看出，最佳k 值为3，即聚类结果分为三大类，选取其中3 个特征，绘制成三维特征空间，其聚类结果如图3所示。聚类结果以及每一类的特征均值分布情况如图4所示。

将聚类结果进行数据可视化整理，得到表6 的聚类结果明细。表6 显示了基于本文的SEG 算法的电力公司信通客户聚类结果，从表中可以看到三类客户的各项特征的均值，通过对聚类结果的分析可以为电力公司客服业务的方案决定提供有力的科学依据。

表6 聚类结果明细Tab.6 Details of clustering results

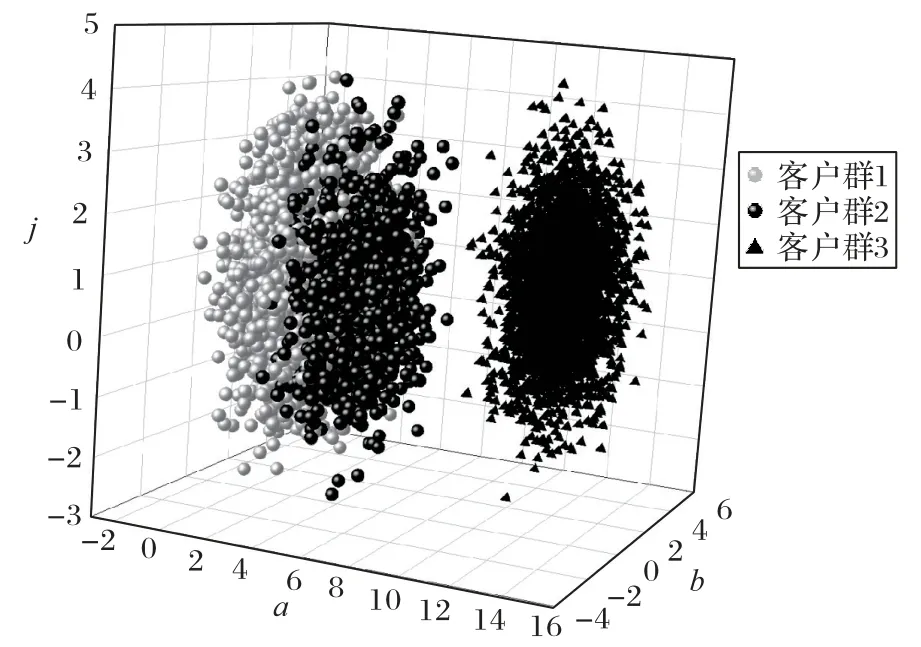
图3 三特征聚类结果Fig.3 Clustering results of three features

2）结果分析。

将仿真结果进行总结整理，得到了表7。从表7中可以看出，客户被分为了三类，以下是对每一类客户的分析。

客户群1 该类客户所占比重为30%，占有相当的比重。该类客户的月均消费是11.76 万元，处于非常高的一个消费水平；合同容量500 kVA 是用电容量需求非常高的，用电类型多为大工业用电；拖欠金额4.15 万元，说明这一类客户电费拖欠比较严重；用电匹配度0.97，说明该类客户的安全用电意识整体来说比较高。所以总体而言，这类客户总体价值处于一个高水平。

客户群2 该类客户所占比重为55%，客户数量所占比重最高。该类客户的月均消费是1.56 万元，处于低等消费水平；合同容量是80 kVA，用电容量需求不高，用电类型多为工商业用电；拖欠金额0.37 万元，说明这一类客户电费拖欠情况比较轻微，诚信度很高；用电匹配度0.85，说明该类客户的安全用电意识整体来说一般。所以总体而言，这类客户总体价值处于一个中等水平。

客户群3 该类客户所占比重为15%，是客户数量最少的一类。该类客户的月均消费是4.15 万元，处于中等消费水平；合同容量110 kVA 是用电容量需求较高的，用电类型以农业生产用电为主；拖欠金额3.87 万元，说明这一类客户电费拖欠情况有点严重，诚信度不是很高；用电匹配度0.69，说明该类客户的安全用电意识整体来说比较差。所以总体而言，这类客户总体价值处于一个低等水平。

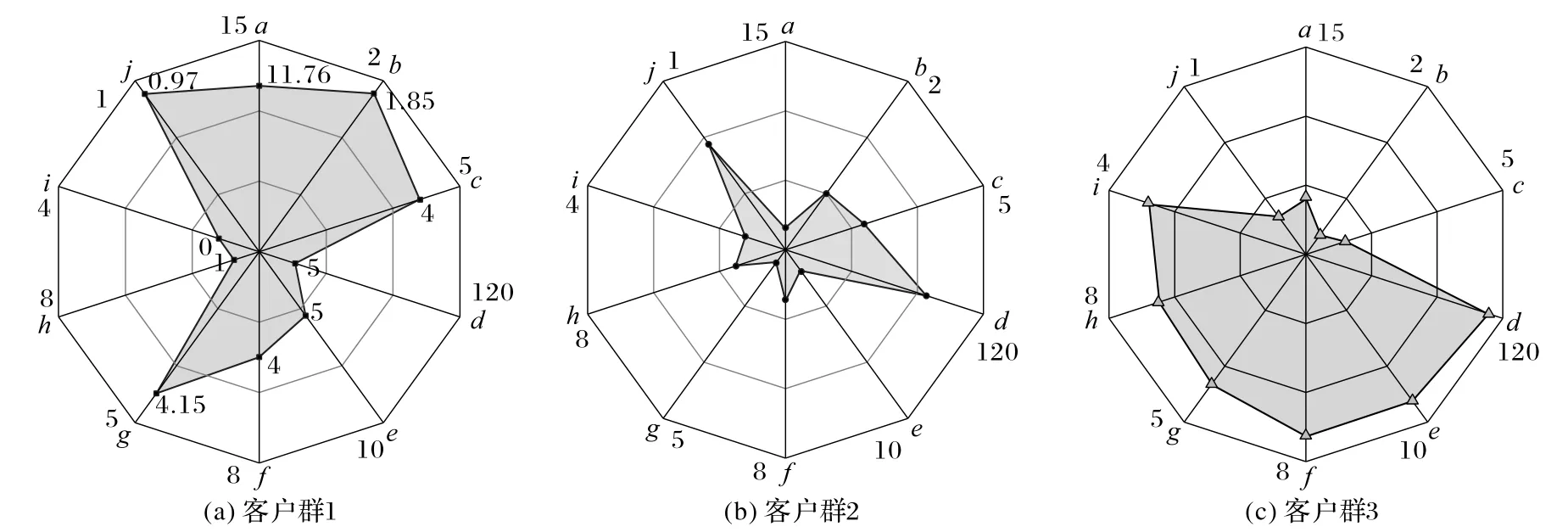
图4 3种客户群特征Fig.4 Three customer cluster features

根据聚类结果的分析，可以针对这三类不同的客户群制定不同的营销策略，以达到精准营销的目的，为客户提供更好的服务，提高客户的满意度，提升公司客服业务的整体效率和降低服务成本。

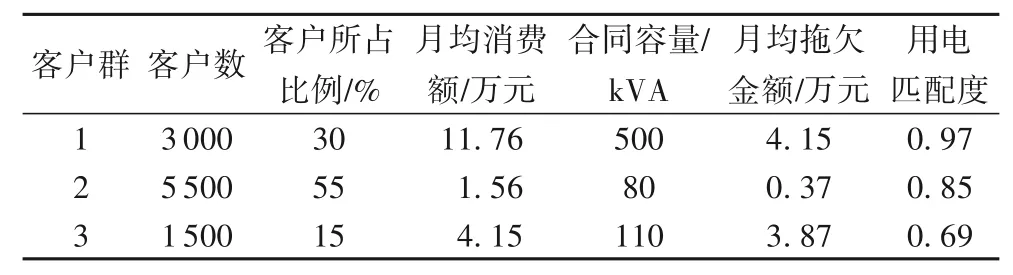
表7 聚类结果Tab.7 Clustering results

3）聚类质量评价。

为验证本文方法对电力公司信通客户数据聚类的效果，本节将本文算法、K-Means 算法以及层次聚类算法对电力公司信通客户数据的测试结果评价指标进行了对比。为了避免偶然性，对上述的算法均重复做了多次测试，并取几次结果的平均值作为最后的评价指标结果。其中，通过FM指标、AR指标、CI 指标、DS 指标以及运行时间这五项指标来对比评价算法的聚类质量，具体测试结果如表8所示。

从表8 可以看出，在数据样本数为10 000 的情况下，本文算法在FM 指标、AR 指标、CI 指标以及DS 指标上均要优于层次聚类算法和K-Means 算法。此外可以看出，本文算法在FM指标和AR 指标上的值都非常接近于1，从这两项指标上来看说明本文算法聚类划分后的簇与标准簇非常接近，聚类效果非常好。在CI 指标上，本文算法也明显优于另外的两种算法，说明本文算法聚类后的簇有不错的紧凑度。在DS 指标上，本文算法虽和层次聚类算法的值比较接近，但还是要略微小一点，说明本文算法的聚类后的簇的分离度要比另外的两种算法的聚类后簇的分离度更大，聚类效果更好。然而从算法运行时间上来看，运行时间最短的是K-Means 算法，其次才是本文算法，最长的是层次聚类算法。不过，本文算法和K-Means 算法在运行时间上的差距也不是特别大，说明本文算法在复杂度上略微差了一些。总体而言，本文算法对电力公司信通客户数据的聚类相较于K-Means 算法和层次聚类算法有更好的效果，只是在运行时间上略微长了一点。

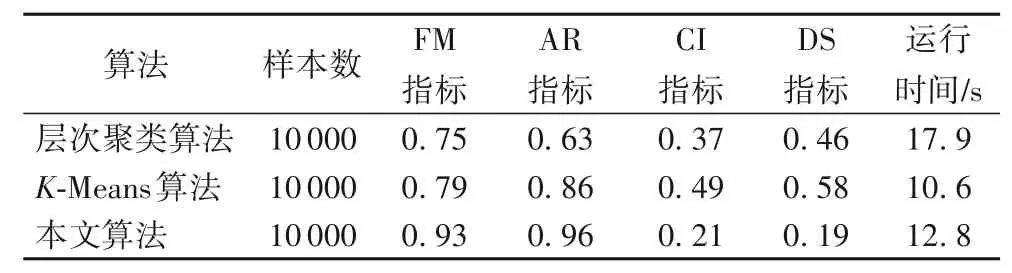
表8 聚类质量测试结果Tab.8 Clustering quality test results

4 结语

本文提出SEG 聚类算法对电力客户进行聚类，该算法采用基于SSE 的手肘法来确定聚类数目的最优值k，再由该k 值来进行基于EM 算法的GMM 聚类算法，提高聚类的全局寻优能力。应用结果表明，本文以聚类质量评价指标FM、AR、CI、DS 和运行时间指标为标准，验证了本文算法比现有的K-Means 与层次聚类具有更好的分类效果、聚类质量和全局寻优性能，并同时拥有良好稳健性。该方法适合于客户分类领域内的应用。

由于本文应用数据集的规模受到限制，因此下一步研究计划将对更大规模数据集进行并行计算分析，并将本文算法应用到电力公司数据分析的其他领域。