基于共享近邻的多视角谱聚类算法

宋 艳，殷 俊

（上海海事大学信息工程学院，上海 201306）

（∗通信作者电子邮箱junyin@shmtu.edu.cn）

0 引言

聚类分析［1］就是按照某个特定标准将一个数据集分割成不同的簇，使同一簇的数据尽可能地聚集到一起。传统的k-means 聚类算法［2］对样本空间有特定的要求，当样本空间不为凸时，算法就会陷入局部最优。与k-means 算法相比，谱聚类算法具有能在任意形状的样本空间上聚类且收敛于全局最优的优点。

谱聚类［3］是一种基于图的聚类方法，且性能高度依赖于相似矩阵。目前，用于构造相似矩阵的方法主要有高斯核函数法［4］、K 近邻法（K-Nearest Neighbor，KNN）［5］和ε-阈值法。高斯核函数一般用于全连接相似矩阵，KNN 和ε-阈值法用于局部连接相似矩阵，三种计量方法均以距离作为衡量单位，对于处在不同密度中的数据点之间的相似关系无法衡量，而数据点之间的相似性不仅跟两者之间的距离有关，同时也跟两者是否处在同一密度区域有关。针对以上问题，本文用共享近邻方法结合经典的高斯核函数方法，提出了基于共享近邻的自适应高斯核函数方法。

多视角谱聚类算法［6-8］在单视角算法的基础上利用不同视角数据之间的相关性以及互补性获得更多有价值的信息，是目前谱聚类研究中的一个重要方向。大部分多视角谱聚类算法在结合多个视角的信息后再次用k-means算法实现聚类，这些方法仍然难以摆脱k-means 算法初始聚类中心不确定的问题。针对以上问题，本文提出基于共享近邻的多视角谱聚类算法（Multi-View spectral clustering algorithm based on Shared Nearest Neighbor，MV-SNN），将改进的相似矩阵相加整合得到全局相似矩阵，同时利用拉普拉斯矩阵秩约束理论，直接通过全局相似矩阵得到最终的聚类结果。

1 相关工作

谱聚类的基本思想是利用从数据中得到的更低维的特征矩阵实现聚类，主要依靠两个部分完成聚类工作：1）图的构造；2）对构造好的图诱导出拉普拉斯矩阵并作特征分解，将数据嵌入到特征向量空间，最后再次使用k-means 算法实现聚类。在多视角谱聚类算法中，Kumar等［9］提出了协同正则多视角谱聚类（Co-regularized Multi-view Spectral Clustering，CRSC）算法，Zhan 等［10］提出了图学习的多视角谱聚类（Graph Learning for Multi-View clustering，MVGL）算法。

1.1 协同正则多视角谱聚类算法

Kumar 等［9］将用于有监督训练的协同思想应用到无监督谱聚类算法中，算法在多视角数据聚类结构一致性假设的前提下，同时考虑每个视角谱聚类算法的优化情况和不同视角之间的差异情况，提出成对优化模式和基于中心的优化模式。后者对所有视角的数据优化出一个中心特征嵌入矩阵U*来平衡其他视角的数据，目标函数如下：

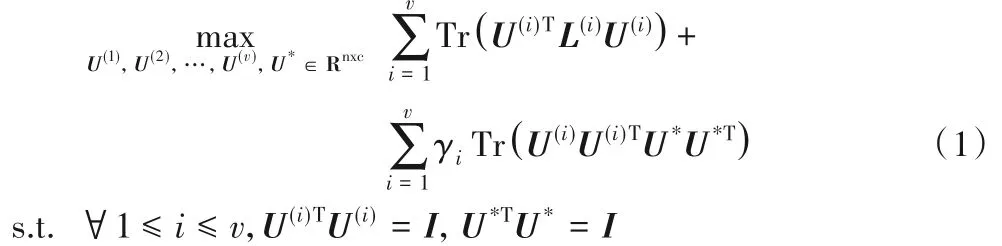
其中：v表示视角个数；Tr（）表示求迹运算；I表示单位矩阵；参数γi为正则化加权项，它的大小代表了视角i 的重要程度，且需要人工指定。max Tr(U(i)TL(i)U(i)) 是第i 个视角的谱聚类优化函数，-Tr(U(i)U(i)TU*U*T) 则表示第i 个视角的特征嵌入矩阵和中心嵌入矩阵的误差函数，通过最小化差异函数来平衡中心嵌入矩阵和各个视角特征嵌入矩阵之间的差异，将两者需求进行整合得到最终的式（1），最后再对矩阵U*实施k-means方法得到聚类结果。CRSC 算法是多视角谱聚类算法的开端，之后的多视角聚类方法均是在各个视角聚类结构一致的假设条件下开展工作。

1.2 图学习的多视角谱聚类算法

首先将v个视角下通过KNN算法得到的相似矩阵S(i)乘以对应权重Q(i)相加整合；然后构造出一个全局相似矩阵A；最后通过最小化误差函数来最小化两者之间的差异，从而获得全局相似矩阵A的值。同时该优化框架结合拉普拉斯矩阵秩约束方法，根据全局相似矩阵得到聚类结果，目标函数如下：

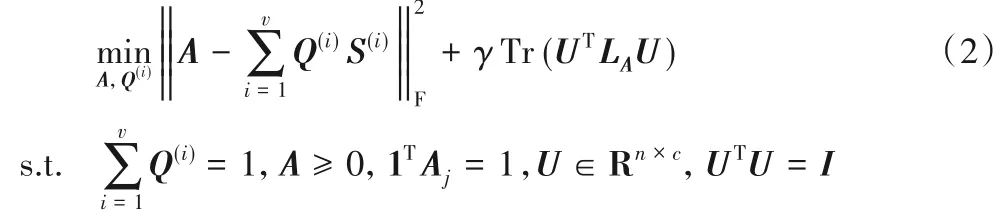
其中：Aj表示矩阵A的第j列向量，列和为1；γ为权衡参数，用来控制后一项的比重；矩阵L为矩阵A所对应的拉普拉斯矩阵。

由于相似矩阵的构造方法对谱聚类算法有很大影响，而MVGL 算法在前期使用KNN 算法构造相似矩阵，所以它最终的聚类准确率会受到一定影响。

2 相似矩阵构造方法

谱聚类算法中相似矩阵的构造方法最经典的应该属于高斯核函数和KNN算法。

高斯核函数：

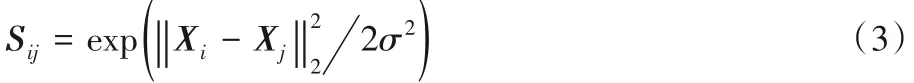
其中：Xi和Xj表示两个数据点；σ 是一个需要人工指定的参数。该构造方法中，两点的相似度只与两点间的欧氏距离有关，但是只以距离作为衡量相似度的标准，对应不同密度的簇就无法处理。

KNN 算法是一种高斯核函数的局部连接构造方法，它并不能解决存在密度差异的两个数据点之间的相似情况，而相似值应同时满足空间上相近的两个数据点之间具有较高的相似度且位于同一个簇的数据点具有较高的相似度两个要求。本文利用共享近邻的思想来构造相似矩阵，该方法根据数据集流形结构的特点来增强同簇数据点之间的相似性。

2.1 基于共享近邻的构造方法

数据点Xi和Xj之间的共享最近邻（Shared Nearest Neighbor，SNN）：

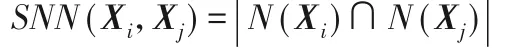
其中：N(Xi)表示与点Xi最近的前k个点构成的集合；N(Xj)表示与点Xj最近的前k个点构成的集合。如图1所示，两个对象A、B 的8 个最近邻中，有4 个（深色）是A、B 共享的，因此这两个对象之间的共享近邻个数为4。

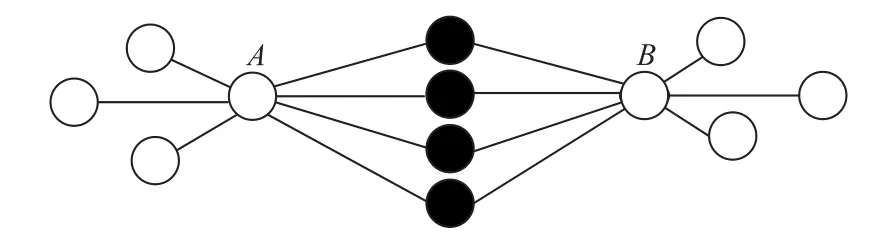
图1 共享近邻个数示意图Fig.1 Schematic diagram of number of shared neighbors

结合共享近邻的思想，给出任意两点Xi和Xj之间的相似度度量Sij，基于共享近邻的自适应高斯核函数：

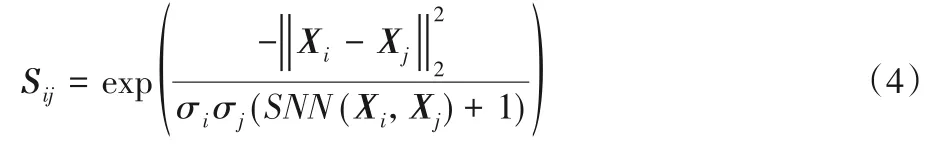
其中：σi和σj分别为点Xi和点Xj到各自第p 个近邻的欧氏距离（p 一般取7），使用特定的缩放参数σi和σj，不仅能够解决高斯核函数中σ 需要人工指定的问题，而且也能捕捉到两点邻域内数据点分布的稀疏稠密情况从而得到更好的聚类结果。为了进一步验证以上函数有效性，本文在以下两种具体情形中对其结果进行分析：

1）假设当两点Xi和Xj距离较近时，则值较小，于是Sij值变大，使得相近的数据点具有较高的相似度。

2）假设当数据点Xi和Xj位于同一簇中，数据点Xi和Xk位于不同簇中，且时，统计它们之间共享近邻的个数，有SNN(Xi，Xj)＞SNN(Xi，Xk)（同一密度簇中的共享近邻个数更多），进而得到相似度Sij＞Sik，使得位于同一簇上的两点具有更高的相似度。

因为谱聚类算法适合处理比较稀疏的数据，为了得到更精确的结果，本文进一步对相似矩阵进行稀疏化处理，只有两个数据点之间的共享近邻数大于阈值δ，相似度Sij值才不为0，具体的处理过程总结在下列的算法1中。

算法1 相似矩阵的构造方法。

输出 相似矩阵S。

if 数据点Xi在点Xj的k 近邻空间中且数据点Xj在点Xi的k 近邻空间中

if SNN(Xi，Xj)＞阈值δ

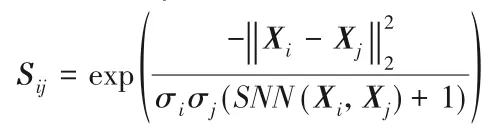
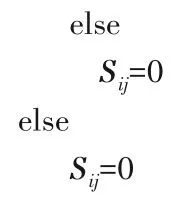
在该算法中，主要有两个参数：k 和δ。k 值过大则会导致最终只有一个簇，k值过小则会导致每个数据点都自成一簇；δ值根据k值而定，一般情况下，δ=k/2。

2.2 相似矩阵散点图实验

为了验证算法1 的有效性，将KNN 算法和算法1 在人工数据集（三环数据集，具体介绍见4.1 节）上构造相似矩阵（两者的参数k 均取10）并通过散点图表示，如图2 所示。所测试的数据集为其中第1 个数据点到第100个数据点属于第1 个簇，第101 个数据点到第200 个数据点属于第2个簇，第201个数据点到第300个数据点属于第3个簇，一共有3 个簇；因此理论上该数据集得到的相似矩阵应该是标准的对角块结构。

图2中的散点表示两个数据点相似：从图2（a）可以看出，由算法1 得到的相似矩阵图中的点基本都集中在对角块上，说明达到了簇内数据点之间高度相似的要求；在图2（b）由KNN算法得到的散点图中，很多点散落在对角结构之外，说明不同簇的很多数据点之间依然相似，并没有达到相似矩阵的构造要求。

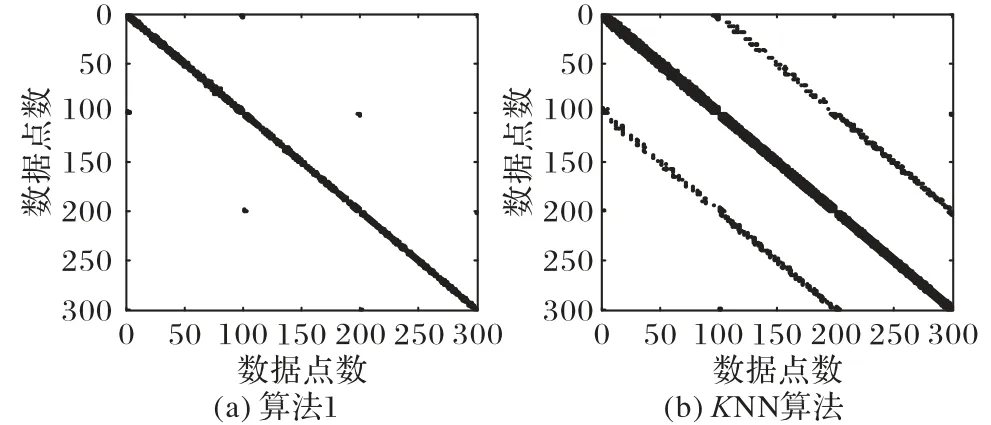
图2 三环数据集相似矩阵的散点图Fig.2 Scatter plots of similarity matrix of three-circle data set

3 基于共享近邻的多视角谱聚类算法

为了提高算法性能，在进行多视角数据融合前，MV-SNN算法先对单视角数据构成的相似矩阵进行优化；然后将各个视角优化后的相似矩阵相加整合得到一个全局相似矩阵；最后利用秩约束理论，直接通过全局相似矩阵得到最终的聚类结果。

3.1 目标函数

为了保留各个视角携带的信息，本文将不同视角下的相似矩阵通过相加的方式融合为一个全局相似矩阵，表示如下：

其中：S(i)*表示优化过的第i 个视角的相似矩阵（优化过程在3.3节给出），因为相似矩阵，它满足下列定理1。

定理1相似矩阵S的连通分支数c等于其对应的拉普拉斯矩阵的特征值为0的个数。

这个定理表明，如果满足rank(L)=n -c 这个条件（n 是数据点的个数），即L 的前c 个最小特征值之和等于0，那么就可以直接通过相似矩阵S得到最终的c个簇。

根据文献［11］，有以下等式：

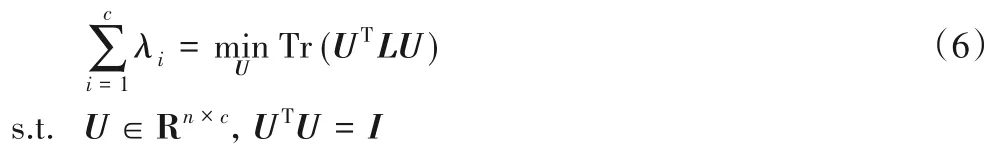
其中：λi表示拉普拉斯矩阵L 的第i个特征值，L=D -S，D 表示度矩阵，它是一个对角阵，对角元素是矩阵S 的每列和，U是由拉普拉斯矩阵L 前c 个最小特征值对应的特征向量组成的矩阵。

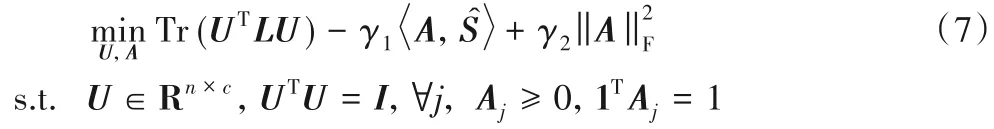
其中：γ1、γ2是权衡参数表示矩阵A与矩阵的Frobenius 内积。为了避免出现Aj中有一个元素的值为1，而其余值为0的情况，添加F范数来平滑矩阵A中的元素。通过最小化目标函数（7），最终可以得到相似矩阵A和矩阵U。

3.2 目标函数求解

由于目标函数（7）中有两个变量，本文将该问题分为两个子问题：

1）固定矩阵U，更新矩阵A，目标函数变为：

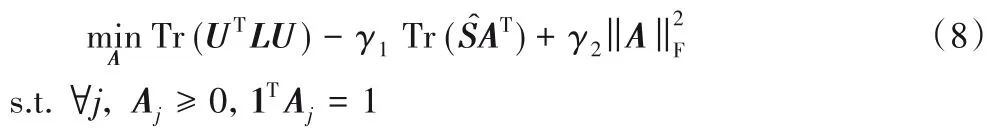
因为每列都是独立的，按列进行更新，则式（8）的拉格朗日函数是：

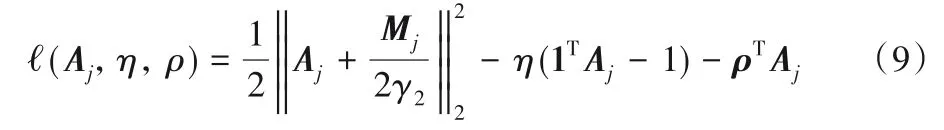
其中：Mj是矩阵M 的列向量，矩阵M 的元素Mij=分别是矩阵U 的第i 列和第j 列向量；η和ρ是拉格朗日乘子。

根据Karush-Kuhn-Tucker（KKT）准则［12］可以得到：

其中(⋅)+表示取非负实数。在矩阵A 中只保留每个数据点的最近的m 个值，同时根据得 到值为列向量Aj中值不为零的个数γ2=

2）固定矩阵A，更新矩阵U，目标函数变为：

问题（11）对于变量U 的最优解是其对应拉普拉斯矩阵L前c 个最小特征值对应的特征向量组成的矩阵，两个子问题交替迭代，最终可以得到矩阵A 和U 值。具体的算法流程总结在下列的算法2中。

算法2 基于共享近邻的多视角谱聚类。

输出 具有c个连通分支的相似矩阵A。初始化 全局相似矩阵矩阵U 由矩阵A 对应的拉普拉斯矩阵L的前c个最小特征值对应的特征向量组成

通过式（11）更新矩阵U

until 函数收敛

3.3 初始相似矩阵的优化

为了使各个视角初始相似矩阵的簇结构更加突出，本文在各个视角的初始相似矩阵S 的基础上（S 在算法1 中给出），根据定理1的结论，对矩阵S进行秩约束得到新的矩阵S*。目标函数如下：

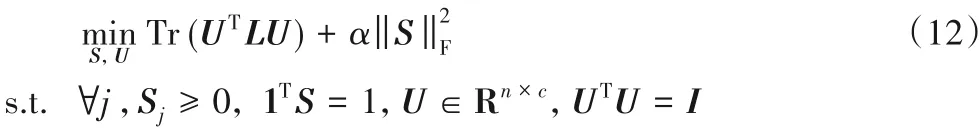
其中：α是正则化参数，矩阵U是由矩阵S对应的拉普拉斯矩阵L前c个最小特征值对应的特征向量组成的矩阵。该目标函数有两个变量S和U，同样将这个目标函数分为两个子问题。

1）固定矩阵U，更新矩阵S，目标函数为：

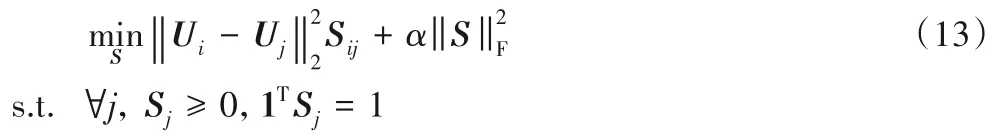
式（13）的拉格朗日函数是：

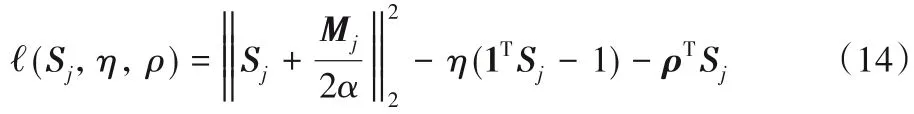
2）固定矩阵S，更新矩阵U，目标函数变为：

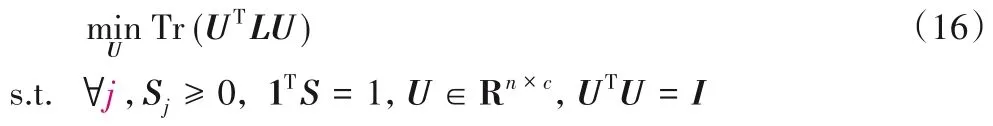
问题（16）对于变量U 的最优解与式（11）相同，两个子问题交替迭代，最终可以得到矩阵S 和U 的值。具体的算法流程总结在算法3中。

算法3 初始相似矩阵的优化。

输入 v个视角的相似矩阵S，聚类个数c；

输出 更新后的v个视角的初始相似矩阵S*。

初始化 式（13）中，初始的矩阵U的值通过初始矩阵S对应的拉普拉斯矩阵L前c个最小特征值对应的特征向量得到。

3.4 收敛性分析

在3.2 节的目标函数求解中，式（8）是凸函数，同时由式（11）的拉格朗日函数推导出的海森（Hessian）矩阵是半正定的（详细证明参考文献［13］），可以得到式（11）的目标函数是凸函数，综上可以得到式（7）收敛的结论。同理3.3 节中的两个子函数（13）和（16）也是凸函数，所以式（12）收敛。具体的收敛实验在4.3.3节给出。

4 实验与分析

实验在两个人工数据集和两个真实数据集上进行。在人工数据集上，对提出的MV-SNN 算法进行测试；在真实数据集上，将MV-SNN算法和下列聚类方法进行对比。

1）SC-Best（Best result of Spectral Clustering）算法。该算法将标准的谱聚类算法在每个视角上分别执行，选取其中结果最好的视角。

2）MVSC（large-scale Multi-View Spectral Clustering via bipartite graph）算法［14］。该算法通过局部流形整合机制来整合多个视角的数据，并通过二分图来提升图构造的速度。该算法中用到的参数r依靠搜寻得到，本文按照作者的建议在对数空间搜寻lg 10r的最优值，设定搜寻范围为[0.1，2]，步长为0.2。

3）CRSC 算法。该算法通过高斯核函数来构造每个视角下的相似矩阵，使用一个协同正则化项来最小化不同视角和全局视角之间的差异性。

4）MVGL 算法。每个视角的相似矩阵由KNN 算法构造，这些单视角下学习的图被融合并通过拉普拉斯矩阵秩约束进行优化以获得所要求的连通分量个数的全局相似矩阵。

5）GSF（Graph Structure Fusion for multi-view clustering）算法［15］。该算法将每个视角下通过KNN 算法获得的相似矩阵通过哈达玛积（Hadamard）的方式进行融合，将融合后的全局图通过拉普拉斯矩阵秩约束直接得到簇划分。

6）MCGC（Multi-view Consensus Graph Clustering）［16］算法。该算法将每个视角通过KNN 算法获得的相似矩阵经过秩优化处理后，求解出一个近似于各个视角对角块结构的全局相似矩阵。

4.1 数据集

4.1.1 人工数据集

1）三环数据集。通过在数据集上分别添加1%和2%的噪声构成两个视角该数据集一共有3个簇，每个簇有100 个数据。因为噪声相对较大，使得不同簇中的数据点非常接近，因此会给聚类带来一定的难度。

4.1.2 真实数据集

1）UCI digits。数据集中有10 个不同的手写数字，从“0”“1”一直到“9”，每个数字有200 个样本，属于一类，一共有2 000 个样本。该数据集一共有6 组特征，选取其中的3 组特征构成3 个视角进行实验：第一个视角是轮廓相关性特征，由216维表示；第二个视角是强度均值特征，由240维表示；第三个视角是Karhunen-Loeve系数特征，由64维表示。

2）NH。数据集有5 个不同的类别，共4 660 张面部图像，一共有3 个视角：第一个是局部二值特征（Local Binary Patterns，LBP），由3 304维表示；第二个是Gabor特征，由6 750维表示；第三个是强度特征，由2 000 维表示。实验使用的数据集汇总在表1中。

表1 多视角数据集Tab.1 Multi-view data sets

4.2 聚类指标

本文通过以下3个聚类指标对聚类效果进行衡量，3个聚类指标的取值均在0～1，值越大表示聚类效果越好。

1）准确度ACC（Accuracy）。

其中：T={T1，T2，…，Tc}表示原始的n 个数据包含真实的c 个类别，P={P1，P2，…，Pc}表 示聚类后n 个数据的c 个预测类别。Ti表示第i 个类别中包含的数据点表示集合Ti中包含的点的个数；Pi表示聚类后第i个类别中包含的数据点表示集合Pi中包含的点的个数。

2）纯度（Purity）P。

3）归一化互信息（Normalized Mutual Information，NMI）RNMI。

4.3 实验结果及分析

4.3.1 人工数据集实验

在人工数据集上对本文提出的MV-SNN 算法进行验证，结果如图3、4 所示。其中：三环数据集上不同簇的数据点分别用点、正方形和叉形描述；双月数据集上不同簇的数据点分别用正方形和叉形描述；两个数据集在算法中设置的参数均为k=10，阈值δ=5。

图3（a）和（b）中的数据点之间的连接边值均由3.3 节的相似矩阵得到，可以看到图中的标注点A处，同簇的数据点之间并没有连接边，而标注点B处，不同簇的数据点间出现了连接边；而由3.1节学习得到的全局相似矩阵绘制的图3（c）中，同簇之间的数据点均有边连接，构成一个连通图，不同簇之间的数据点之间没有连接边，说明三环数据集已经被正确划分。

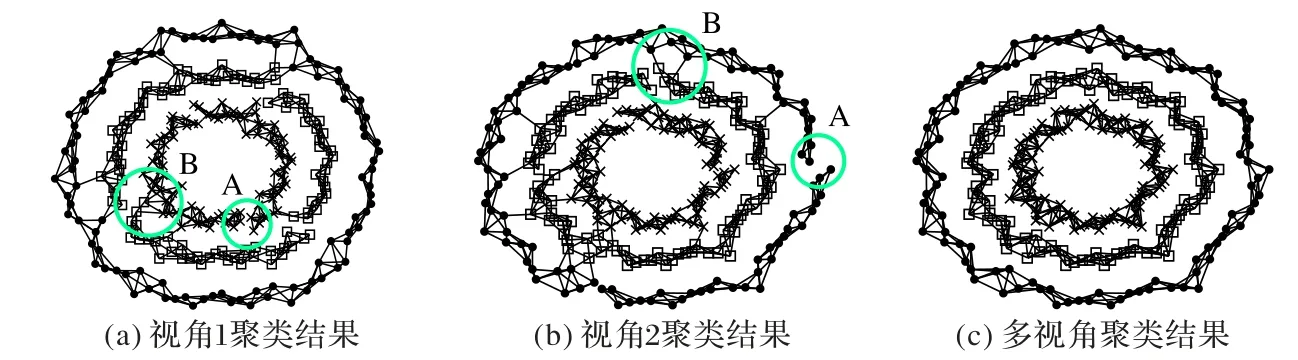
图3 三环数据集聚类结果Fig.3 Three-circle data set clustering results

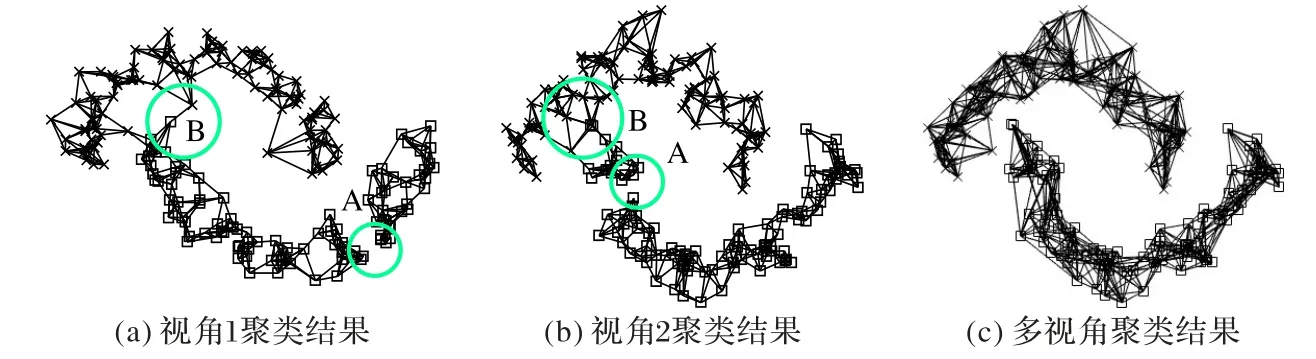
图4 双月数据集聚类结果Fig.4 Two-month data set clustering results

图4（a）和（b）中的标注点A处，同簇的数据点之间并没有连接边，而标注点B 处，不同簇的数据点间出现了连接边，说明数据点被错误划分；而图4（c）中，同簇之间的数据点均有边连接，不同簇之间的数据点之间没有连接边，说明双月数据集已经被正确划分。

从图3（a）、（b）和图4（a）、（b）中可见，单视角谱聚类会出现数据点之间连接错误的情况，而图（c）将两个视角之间的相似信息进行融合，加强同簇数据之间的相似性，从而不会出现单视角下错误的聚类情况。

4.3.2 真实数据集实验

下面6 个算法均以谱聚类算法为基础，SC-Best、MVSC 和CRSC 算法前期各不相同，但最后都需要k-means 算法得到聚类结果；MCGC、MVGL、GSF 和MV-SNN 算法多视角数据融合的方式各不相同，但是最后都是通过拉普拉斯矩阵秩约束理论得到聚类结果。聚类结果如表2 所示，最好的结果均加粗标注。其中：UCI digits 数据集MV-SNN 算法中参数k=18，阈值δ=9；NH数据集MV-SNN算法中参数k=16，阈值δ=8。

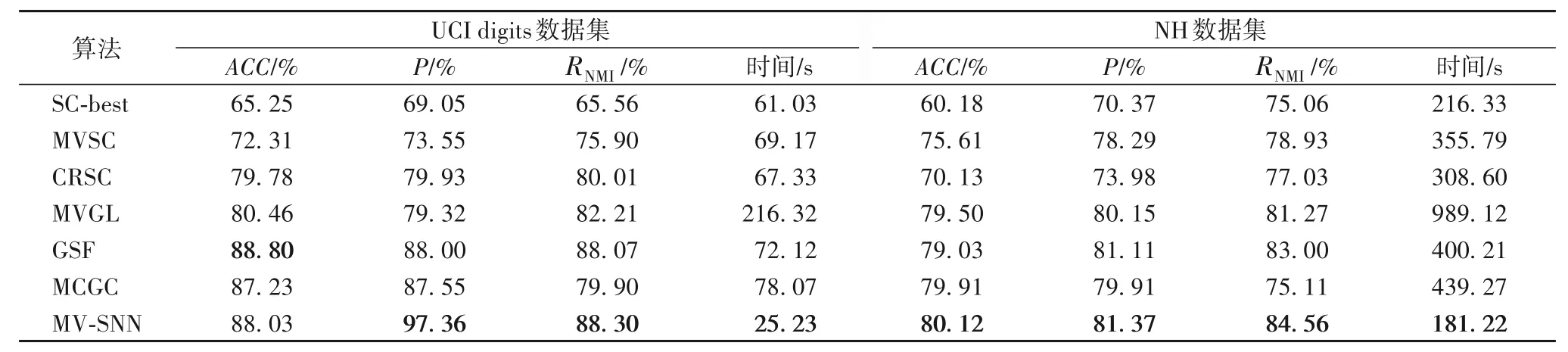
表2 UCI digits和NH数据集聚类结果Tab.2 Clustering results of UCI digits and NH datasets

表2中，对于UCI digits数据集，多视角谱聚类算法的结果都优于单视角聚类结果，说明了多视角聚类的优越性。当簇数较多时，MV-SNN 算法的ACC 结果仅次于GSF 算法但是优于MCGC 算法，GSF 算法采用哈达玛积融合多视角数据，在一定程度上可以摒弃多余信息的干扰；本文采用视角数据相加的方式，对于多视角信息之间的补充有很好的作用，但是也会增加多视角聚类时无用信息的干扰；而MCGC 算法从相似矩阵的图形结构出发，在一定程度上可以使得相似矩阵近似于对角块结构，但是当数据集簇数较多时，对角块结构构造的准确率会有所下降。同时本文采用共享近邻计算数据点之间的相似度，对于不是很稀疏的数据集，参数k的取值控制在20以内便能探测到数据点之间的相似信息，因此聚类时间效率会明显优于以上几个算法。

对于NH 数据集的高维复杂性，以上所有算法在3个指标上的结果均逊于UCI digits 数据集的结果，但是当簇数较少时，由于MV-SNN 算法采用了新的相似矩阵构造方法，该方法对高维数据有很好的适用性，以及采用新的簇划分方法，从而聚类性能优于其他的多视角谱聚类算法，且在聚类时间上几乎减少50%。

4.3.3 收敛性验证

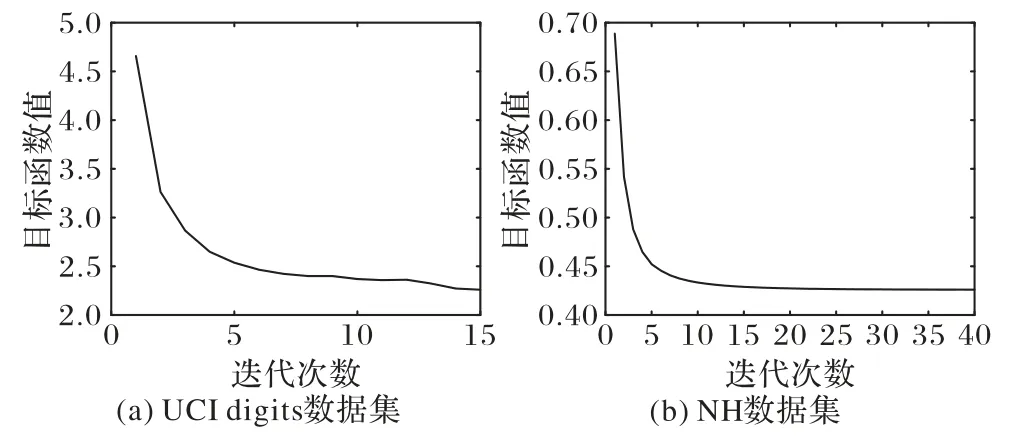
图5 UCI digits和NH数据集的收敛曲线Fig.5 Convergence curves of UCI digits and NH datasets

5 结语

基于共享近邻的自适应高斯核函数在谱聚类相似矩阵构造环节，用欧氏距离和局部密度两个指标来综合衡量数据点之间的相似性，可以应对不同密度的数据簇，得到更合理的相似性分布；同时多视角聚类中采用视角信息相加的方式融合多个视角的信息，比单视角聚类结果更好；最后MV-SNN 算法采用拉普拉斯矩阵秩约束的方法，直接通过相似矩阵得到最终的聚类结果，而其他谱聚类算法后期仍要使用k-means 算法，又会带来初始中心点不确定的问题。实验证明，MV-SNN算法相较于其他多视角谱聚类算法，聚类效果有很大提升。在未来工作中，还要对多视角数据的融合方式进一步研究，由于各个视角所携带信息的不同，直接采用等量权重进行融合不太合理，因此考虑采用信息熵来衡量各个视角数据所携带的信息，进一步优化权重分布。