输水隧洞爆破引起洞内和地表振动特性研究

史 吏，李 进，孙宏磊，刘增伟，姚 康

(1.浙江工业大学 土木工程学院，浙江 杭州 310023；2.杭州市千岛湖原水股份有限公司，浙江 杭州 310016；3.浙江大学 建筑工程学院，浙江 杭州 310058)

目前，隧洞爆破施工引起的环境振动问题得到了广泛的关注。国内外学者通过研究爆破振动速度的传播和衰减规律，得到了爆破振动预测公式。唐海等[1]和张天军等[2]分别运用量纲分析法和非线性回归法得到了反映场地因素、地形因素和高程放大效应的爆破振动衰减公式。Holmberg等[3]提出了基于点源爆破的远场振速数学模型，Arora等[4]在Holmberg模型的基础上补充了柱形装药的影响。在爆破振动主频研究方面，孟海利等[5]基于黏弹性介质中地震波的传播理论，推导了振动主频与装药量、爆心距的函数关系式。武汉大学卢文波团队从无限弹性岩体球形药包激发应力波解析解出发[6]，提出考虑多种地质因素影响的隧洞钻爆开挖爆破振动主频衰减公式[7]，并得到有限元模型[8]及其与现场实测数据的对比验证[9]。李玉民等[10]发现，水平振动的主频(3～18 Hz)更接近地表建筑物的自振频率，因此爆破的水平振动比垂直振动更容易与建筑物产生共振。叶海旺等[11]发现爆破振动波穿过地质结构面时，0～15.6 Hz的振动能量占爆破振动总能量的比值可增大63%。当爆破振动波到达地表时，高频分量可转化为较低频率的表面波，其激振频率在15 Hz以下[12]。但已有的研究成果主要集中在地表振动预测领域，而在隧洞围岩内有溶洞、围岩时，还应控制隧洞内的爆破振动水平，从而保证隧道爆破开挖安全。另外，文献[13]中采用了振速和主频(介质质点最大振幅所对应谐波的频率)结合的振动阈值控制方法，却未提供各类场地条件下的振动主频计算方法。

笔者基于隧洞爆破开挖实测的400余组地表和隧洞内部振动数据，分别研究了地表和隧洞内部振动速度的衰减规律，得到了地表和洞内振速的预测公式。其中，特别研究了爆破振动主频与装药量、爆心距的关系，建立了地表和隧洞内部振速主频的预测公式，并与已有研究结果进行对比验证，研究结果可为预测类似隧洞爆破的振动速度和主频提供技术参考。

1 地表爆破振动测试与分析

1.1 地表爆破振动测试方案

杭州某输水隧洞主要采用爆破开挖，易引起周边环境过大振动。因此，该隧洞爆破施工的一个重要问题是如何控制环境振动。该输水隧洞下穿在建天然气管线，天然气管道已铺设完毕(尚未通气)，管线与地表净距约为0.5 m，为确保隧洞爆破开挖时管线的振动安全，在管线正上方的水泥路面布设振动传感器，如图1所示。隧洞拱顶距地面11.1 m，覆盖层材质自上而下分别为含碎石粉质黏土和强风化粉砂岩，爆破开挖进尺约为1.6 m，在6 个循环回次后，掌子面爆破开挖对测点位置振动影响已较小，因此选择6 个循环回次为一组数据进行比较。测点到隧洞外轮廓线的水平距离为5.5 m，如图2所示。使用专用胶水将传感器置于地面，如图3所示。

图1 隧洞、天然气管线和振动测点相对位置关系剖面图Fig.1 Section view on tunnel, gas pipeline and vibration monitoring point

图2 隧洞、天然气管线和振动测点相对位置关系平面图Fig.2 Plainviewon tunnel, natural gas pipeline and vibration monitoring point

图3 现场测点安装情况Fig.3 Installation of field monitoring instruments

爆破振动信号为短时、非周期性信号，为选择合适的爆破测振传感器，首次爆破振动测试对比3种振动传感器，分别为941B型拾振器、AC-73三向力平衡加速度计和TCS-B3振动传感器。3种传感器在地表均为三向布设，如图3所示，可分别测得测点位置在径向、切向和竖向的振动速度与振动加速度。首次爆破总药量为60 kg，最大单段药量16 kg，爆心距22 m。表1对比了3 种传感器测得的地表振动加速度峰值。由表1可知：941B型拾振器测得的各向振速均明显偏小，但AC-73加速度计与TCS-B3传感器测得的地表三向加速度值较接近，因此选用TCS-B3振动传感器进行后续的爆破振动测试。

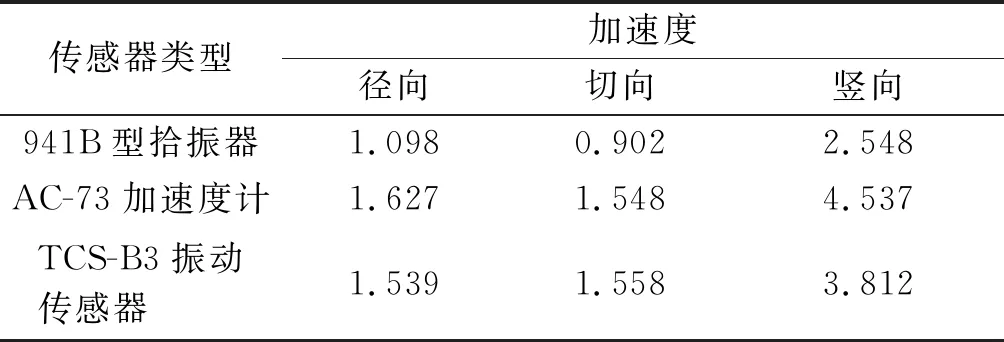
表1 首次爆破中3 种传感器的测试结果对比

1.2 地表振速衰减规律

引入比例距离SD[14-15]以同时考虑装药量和爆心距对爆破振速的影响，即

(1)

式中：R为爆心距，m；Q为单段最大装药量，kg。则地表峰值振速PPV(Peak particle velocity, cm/s)的计算公式为

PPV=K·SDα

(2)

式中：K为场地系数；α为衰减系数。

表2统计了各次爆破的爆心距、单段最大药量和相应的爆破振动峰值速率。采用式(2)对表2中振速数据进行拟合，可得场地系数k和衰减系数α的拟合值，如表3所示。

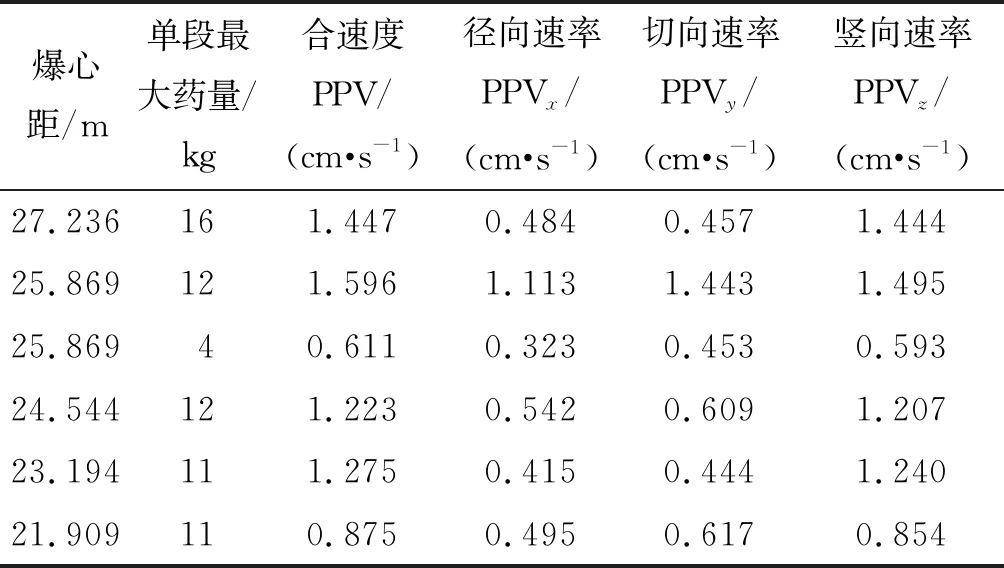
表2 质点峰值振速Table 2 PPV of ground vibration

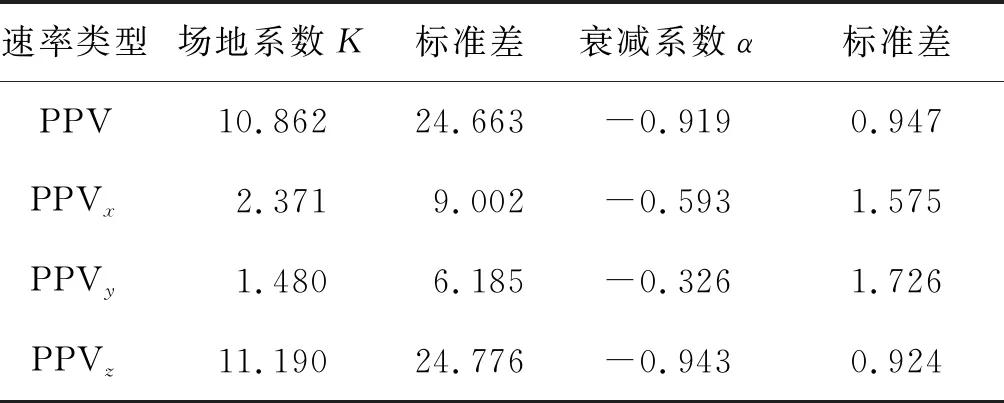
表3 振速衰减公式的拟合系数

由表3可知：隧洞爆破开挖引起的地表振动峰值正比于单段装药量、反比于爆心距。同时，地表振动以竖向分量为主，其场地系数明显高于径向和切向振动分量。

1.3 地表振速主频预测公式及验证

隧洞爆破开挖各进尺下，图1所示地表振动测点的径向、切向和竖向振动主频统计数据如表4所示。

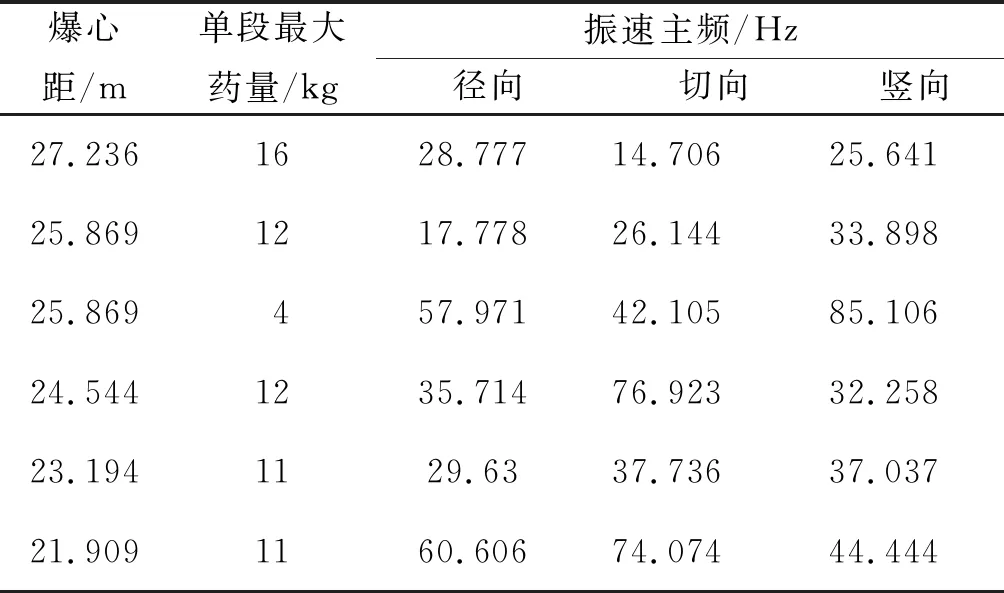
表4 地表实测振动主频Table 4 Measured main vibration frequencyatground surface

《爆破安全规程》[13]将爆破振动主频作为判断结构振动安全的主要依据之一。孟海利等[5]通过求解黏弹性介质中球面波波函数的特定解，推导出振动频率f与装药量Q和爆心距R的关系式为

(3)

式中a1，a2为常数。式(3)可改写为

(4)

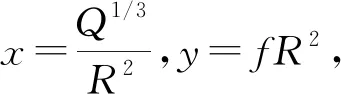
(5)

运用式(5)对表4中的径向、切向和竖向振速主频实测数据进行拟合，得到相应的拟合曲线及拟合公式，如图4所示。

系数a1，a2拟合值统计如表5所示。其中a1为10-3量级，正值，径向、切向和竖向主频预测公式系数a1分别为5.57×10-3，4.53×10-3，7.18×10-3；a2为10-6量级，径向、切向和竖向主频预测公式系数a2分别为2.26×10-6，7.68×10-6，-1.69×10-6。

结合三峡永久船闸闸室位置岩体爆破开挖，周俊汝等[8]对斜长花岗岩中的2 次台阶爆破进行了现场振动实测，两次爆破的最大单响药量约为76 kg，各振动测点位置的爆心距在10～30 m范围内，周俊汝等[8]将各测点实测数据进行傅里叶变换，获得了爆破振动主频随爆心距的衰减情况，图5中包括了式(4)的竖向振速主频预测结果(公式拟合系数取自表5)。对比可知：笔者所提振动主频预测公式计算结果与周俊汝等[8]实测结果吻合较好，说明了本次研究振速主频预测公式的合理性。

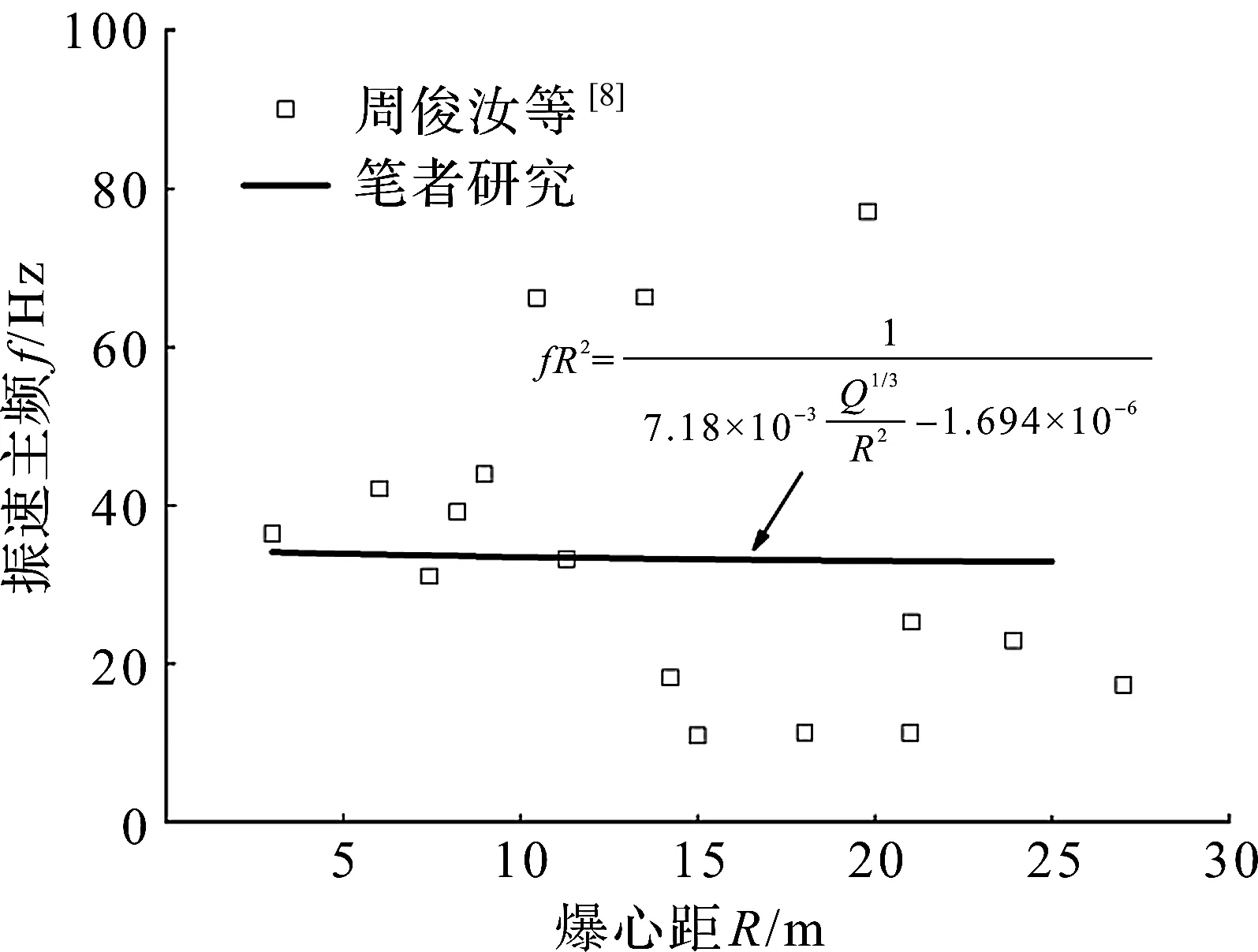
图5 地表振速主频预测公式(4)与周俊汝等[8]实测结果对比Fig.5 Comparison between predicted values from Eq. (4) and field test results from the paper[8] by Zhou on vibrations at ground surface

2 隧洞洞内爆破振动测试与分析

2.1 隧洞洞内爆破振动测试方案

测试段隧洞的洞底高程为-50 m，隧洞开挖洞径为7.3 m，隧洞围岩为凝灰岩。隧洞横贯长约20 m的溶洞，如图6所示，隧洞内部存在围岩薄弱区，需控制洞内的爆破振速，从而防止围岩爆破损伤破坏而造成地下水突涌。

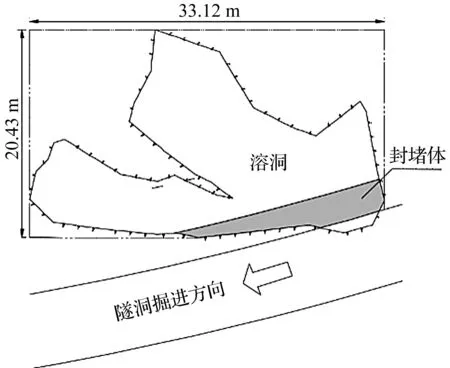
图6 隧洞与溶洞相对位置平面图Fig.6 Plainview on the tunnel and the karst cave

开始测试时，在隧洞侧壁上距离掌子面30 m(M1测点)、40 m(M2测点)、50 m(M3测点)和70 m(M4测点)预留测试孔，测试孔平面和断面位置分别如图7，8所示。隧洞爆破掘进时，掌子面与测试孔的距离逐渐增大。

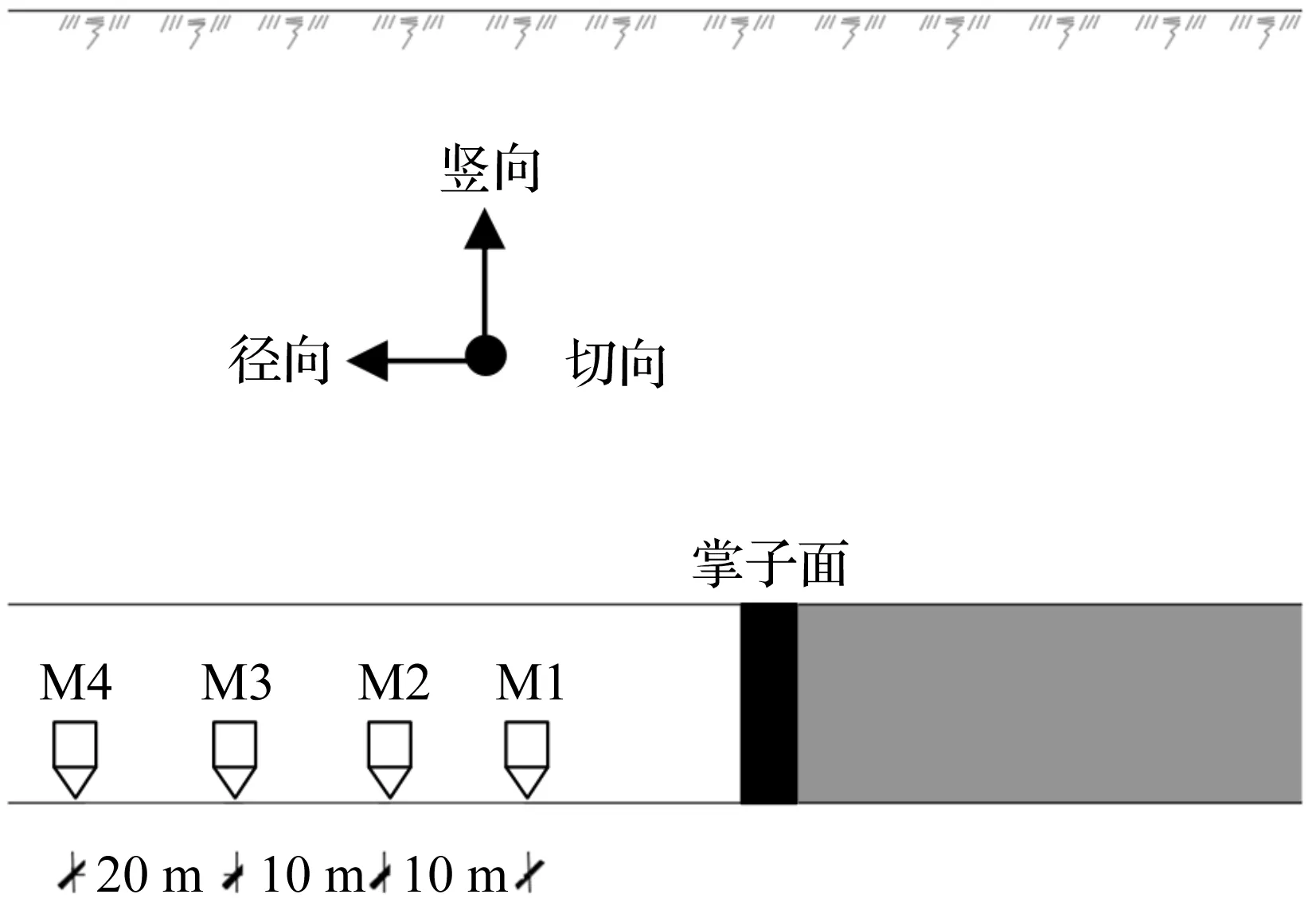
图7 洞内爆破振动测点位置Fig.7 Location of monitoring point inside the tunnel

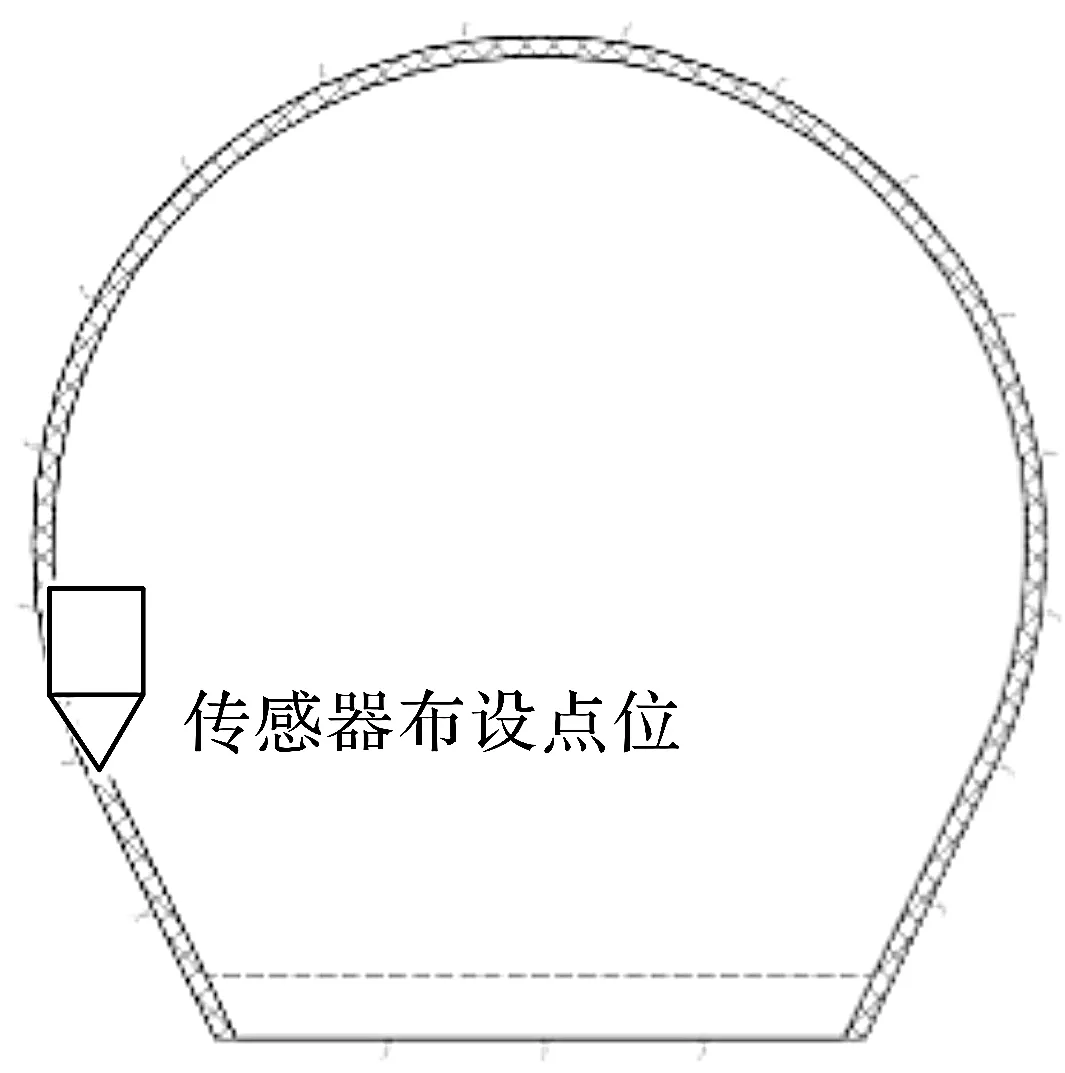
图8 隧洞内传感器布设点位Fig.8 Section view on monitoring point inside the tunnel

将洞内侧壁测试孔的大小取为20×20×40 cm，用专用黏结剂将传感器固定在侧壁测试孔中，如图9所示。

图9 隧洞洞壁测试孔中的三向振动传感器Fig.9 Tri-axial vibration sensor adopted inside the tunnel

该段隧洞爆破开挖采用斜眼掏槽、乳化炸药、非耦合装药和非电毫秒雷管等方法。隧洞掌子面的炮孔布置和装药参数如表6所示。

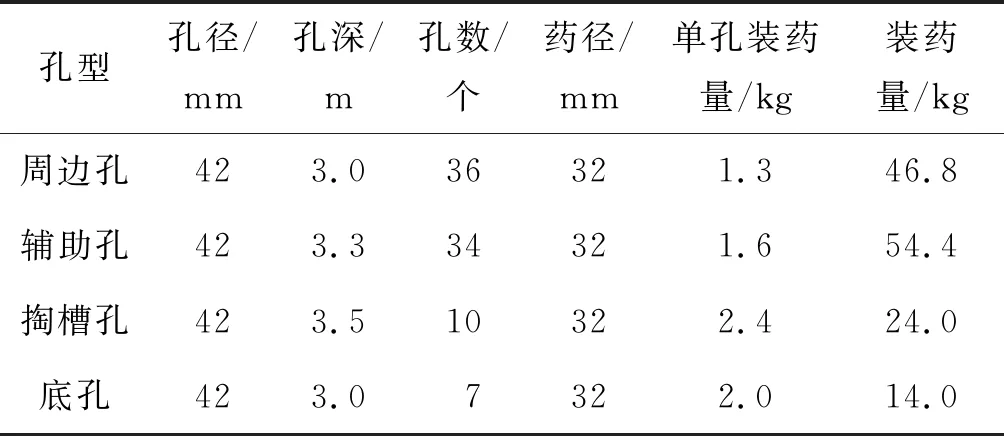
表6 围岩爆破参数Table 6 Blasting parameters of tunnel rock

2.2 隧洞洞内振速特性与衰减规律

以一次总药量119 kg，最大单响药量为24 kg的爆破来分析洞内围岩的振动特性。M1测点的竖向爆破振速时程曲线如图10所示，由图10可知各段导爆管产生的爆破振动信号。

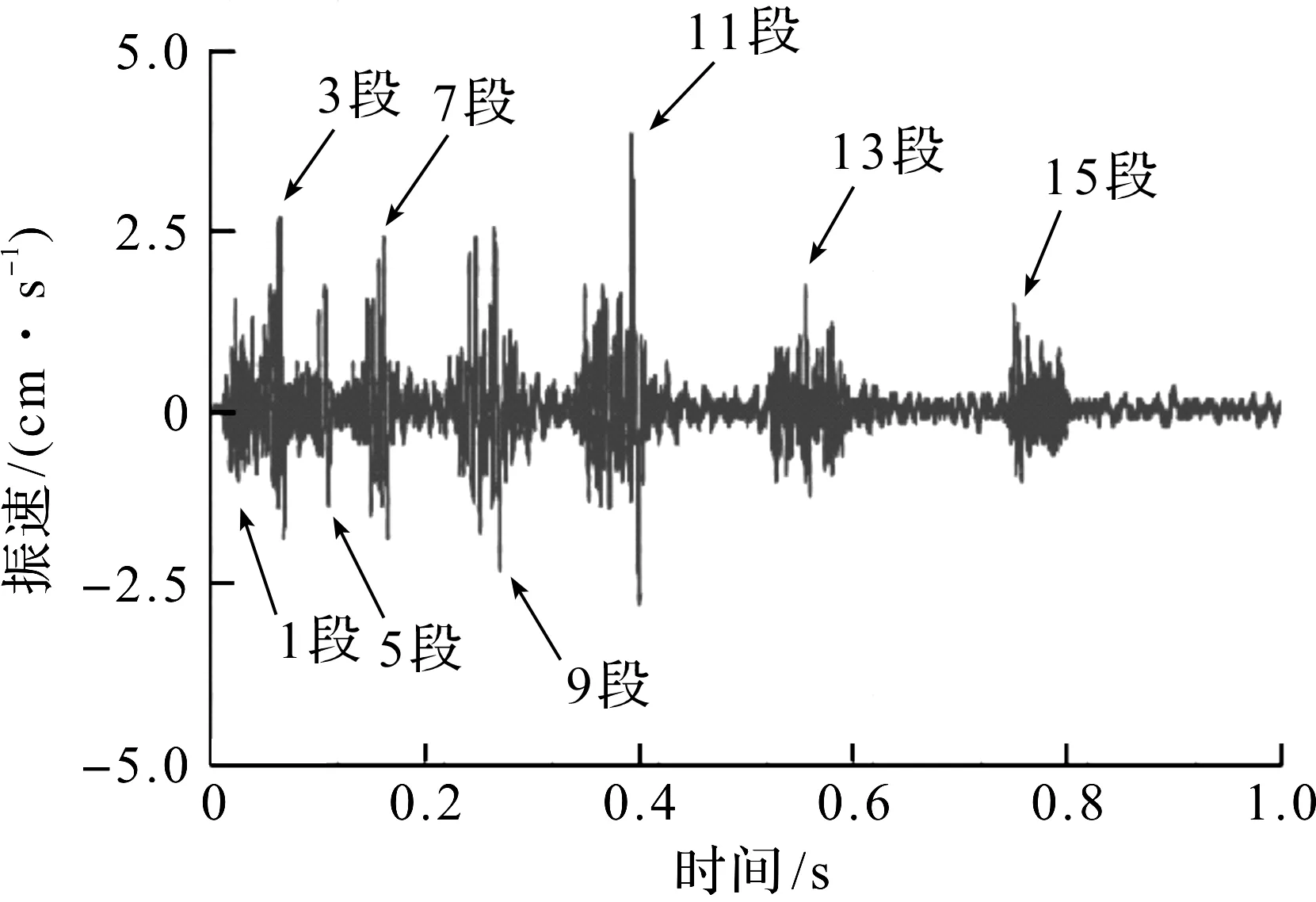
图10 M1测点爆破振速时程曲线Fig.10 Time history curve of blasting vibration velocity at monitoring point M1

不同段别炮孔先后起爆时，近场围岩的振动信号存在明显时间差，即在振速时程曲线图上表现为清晰的波形分离。因而，M1测点(距掌子面30 m)的振动波形分离较为明显(图10)。当测点与掌子面间距增大时，不同段别炮孔爆破引起不同幅值、频率和相位的振动波会在传播路径上叠加形成复合波，故距掌子面40，50，70 m的测点M2，M3，M4的振动波形分离相对不明显。

将396组隧洞内的振动数据以比例距离SD为横坐标，峰值振速PPV为纵坐标，在对数坐标系中绘制图11。由图11可知：在对数坐标下，隧洞内径向和竖向振速峰值均随比例距离的增加而线性降低。径向和竖向振速数据相对集中，而切向振速相对离散，三向振速实测数据中的径向振速平均值相对较大。

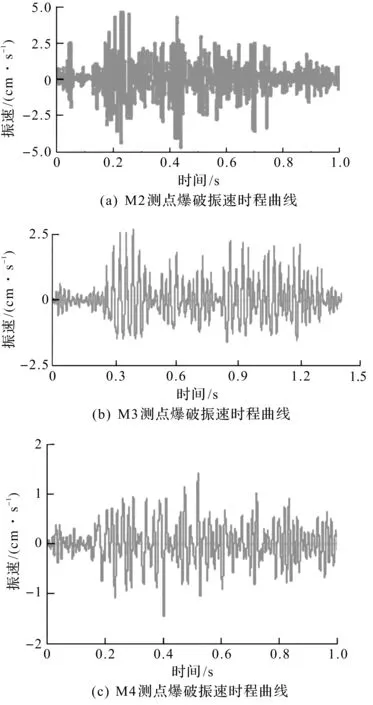
图11 M2，M3，M4测点爆破振速时程曲线Fig.11 Time history curve of blasting vibration velocity at monitoring point M2,M3 and M4

许海亮等[16-17]认为爆破峰值振速的衰减特性与爆破作业面的自由面面积密切相关。此外，Lee等[18]的研究表明围岩节理的波阻抗、不连续结构体的刚度和入射波圆频率Δt对振动波透射和反射有一定影响。受上述因素影响，峰值振速随见侧距离变化情况如图12所示。由图12可知：隧洞洞壁的切向振速的数据离散性较大。

图12 峰值振速随比例距离变化Fig.12 Variations of peak vibrational velocities as the scaled distance

以式(2)形式拟合实测振速，可得隧洞爆破开挖引起的洞内径向、切向和竖向振速预测公式为

(6)

(7)

(8)

式中：Q为最大单段装药量；R为爆心距。将隧洞洞内爆破振速衰减公式的场地系数、衰减系数及其标准差统计到表7中。与表3相比，表7中的场地系数K较大，衰减系数α的绝对值较大，表明洞内振速衰减比地表更快。爆破振动波经过围岩传至地表时，振动主频降低、振速衰减变慢，而洞内围岩振动主频较高，高频分量的振动衰减更快。

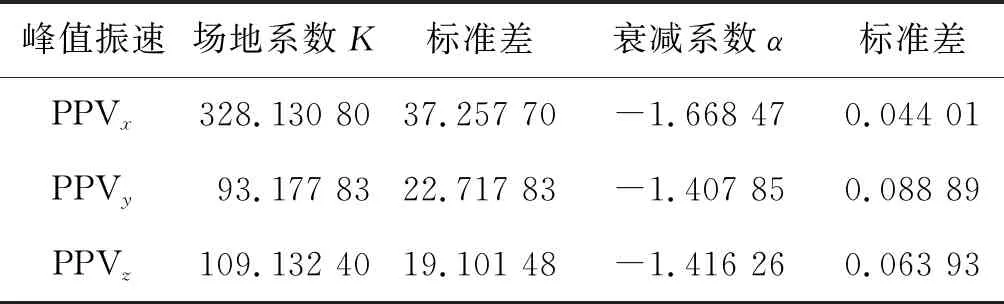
表7 洞内爆破振动衰减的场地系数、衰减系数Table 7 Site and attenuation factors of prediction formula on PPV inside the tunnel

2.3 隧洞洞内振动主频预测公式及验证

在隧洞爆破掘进过程中，江底段Q取值范围为16～24 kg，实测径向、切向、竖向振动主频范围分别为17.316～1 000.073，0.1～2 000.145，15.038～1 334.066 Hz。隧洞洞内振速主频预测仍采用式(5)的构造形式，通过上述实测数据拟合确定式(5)中的系数a1和a2，各拟合曲线如图13所示。

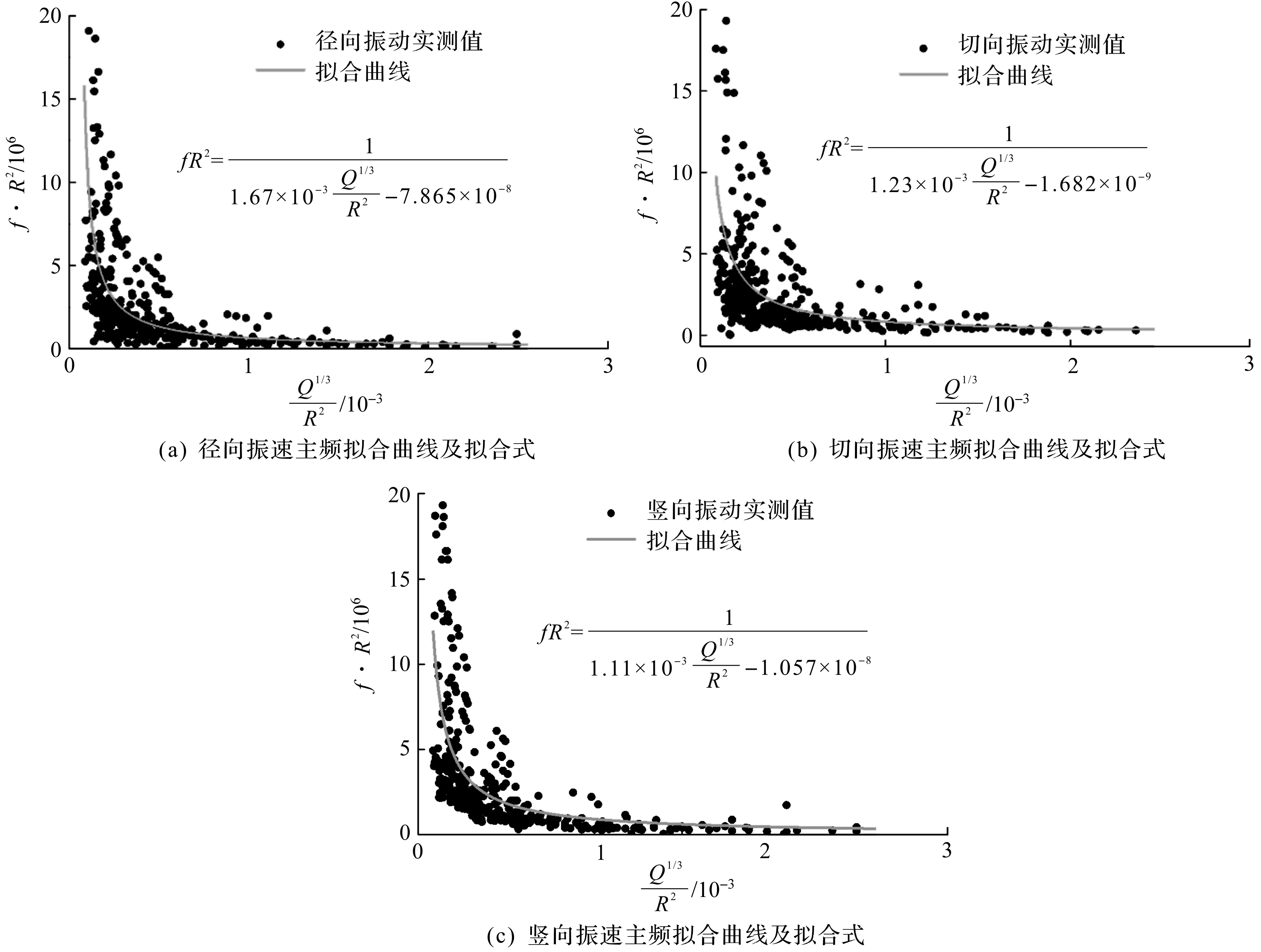
图13 隧洞爆破开挖引起洞内振动的振速主频拟合曲线Fig.13 Fitting curves on the main vibrational frequency at tunnel rock induced by blasting excavation of tunnel

由图13可知：a1为正值，为10-3量级，径向、切向和竖向主频预测公式系数a1分别为1.67×10-3，1.23×10-3，1.11×10-3。系数a2为负值，为10-9～10-8量级，径向、切向和竖向主频预测公式系数a2分别为-7.87×10-8，-1.68×10-9，-1.06×10-8。

表8汇总了各拟合曲线的系数a1和a2。

表8 主频系数a1，a2取值及标准差

刘达等[7]对隧洞爆破引起的洞内振速主频衰减规律展开了理论研究，并结合瀑布沟水库引水隧洞爆破开挖工程实践，实测了洞内爆破振速主频。引水隧洞位于花岗岩层(属于硬质岩)，断面为圆形，设计采用全断面爆破作业，崩落孔第9段为装药量最大段(Q=19.8 kg)，洞内布置3个振速测点，随着隧洞爆破掘进，可得不同爆心距R下的测点振速时程曲线，继而分析可得不同R下的振速主频，如图14所示。图14还包括了式(4)切向振速主频预测结果(公式拟合系数取自表8)。与刘达等[7]实测结果对比可知：笔者所提振动主频预测公式计算结果与其吻合较好，说明了笔者隧洞内部振速主频预测公式的合理性。

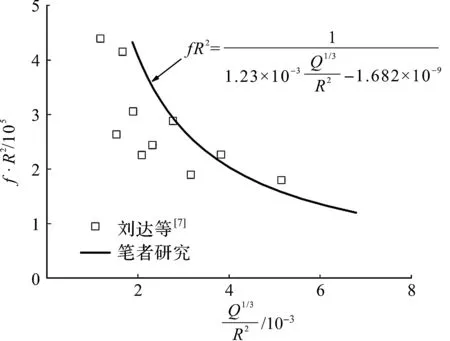
图14 洞内振速主频预测式(4)与刘达等[7]实测结果对比Fig.14 Comparison between predicted values from Eq. (4) and field test results from the paper[7] by Liu on vibrations inside the tunnel

3 结 论

基于某输水隧洞爆破开挖过程中402 组爆破振动实测数据，分别对地表以及隧洞洞内振动速度进行了拟合分析，得到了地表以及隧洞内部的爆破振速预测公式。特别基于振动频率实测数据，建立了隧洞爆破开挖时地表和洞内振速主频与装药量和爆心距的拟合函数关系，并通过与已有爆破振速主频实测结果对比，验证了该拟合函数的有效性。主要结论有：1) 存在土体覆盖层的隧洞爆破开挖时，实测结果表明地表振速的竖向分量最大；凝灰岩中埋深50 m的隧洞爆破开挖时，实测结果表明隧洞洞内振速的径向(隧道延伸方向)分量最大；2) 距掌子面较近时，隧洞洞内振速时程曲线上可清晰分辨不同段别炮孔爆破振动波的贡献。当振动波传播距离增大时，不同幅值、不同频率和不同相位的振动波相互叠加形成复合波，从而距离较远的测点的振速时程曲线上无明显的振动波分离；3) 根据隧洞爆破振动现场测量数据，分别拟合了地表和隧洞内部的萨道夫斯基振速预测公式的场地系数k和衰减系数α；4) 建立了隧洞爆破开挖时，地表和隧洞内部振速主频与装药量和爆心距的拟合函数关系，其拟合系数a1和a2分别取决于单响装药量Q和爆心距R。