天线极化的理论分析及在雷达对抗中的应用

吴昌松，于卫刚，鲁永为，左国银，徐常伟

(中国洛阳电子装备试验中心，河南 洛阳 471000)

0 引言

极化是电磁波一项重要的基本特性，雷达极化学是现代雷达技术的一项重要的分支学科[1]。研究雷达极化目的就是获取和处理极化信息，提高雷达的探测能力、抗干扰能力，以及进行极化雷达成像等[2-4]。

根据天线理论，电磁波的极化是频率和空间指向的函数，在给定频率和空间指向时，天线的极化方式是一定的，当频率和空间指向变化时，极化方式会随之改变，这种变化特性称之为空域极化特性[5-7]。空域极化特性是设计变极化天线的理论基础，而在设计稳定极化的天线时，总是希望在更宽的频带和空域上实现方向图的稳定性[8-10]。由于几何尺寸、加工误差、馈源偏焦等因素的影响，交叉极化总会出现，传统上通常视其为不利因素，无论是进行接收还是发射，一般都希望抑制交叉极化，提高极化纯度[11]。因此，探讨天线极化并将其应用于雷达对抗领域，具有重要的理论和实际意义。

本文以雷达天线理论为基础，研究了天线的极化特性，建立其数学模型，并针对收发天线不同极化方式，给出了天线极化的误差分析，研究了轴比和极化失配因子对接收机灵敏度和雷达接收端干信比的影响，对雷达装备研制及雷达对抗试验评估有一定的参考意义。

1 任意极化波的合成与分解

1.1 分解为两线极化分量

一个任意极化波可分解为2个正交的线极化波，即E(t)=E1cos(wt)u1+E2cos(wt+φ)u2。其中，E(t)是极化平面(即垂直于传播方向的平面)内的电场矢量，E1，E2是2个正交线极化分量场的幅度，比值为ρ。φ是两分量场的初始相位差。根据上述公式中幅度和相位的关系，可分为3种情况：

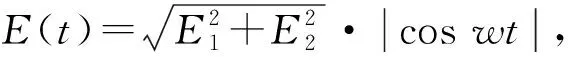
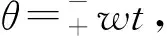
(3) 其他情况时，合成场为椭圆极化波，其幅度与极化方向均随时间而改变。

1.2 分解为两圆极化波

一个任意极化波可分解为2个正交的圆极化波

E(t)=EL[cos(wt)u1-sin(wt)u2]+

ER[cos(wt+φc)u1+sin(wt+φc)u2]，

式中：E(t)为极化平面内的电场矢量；EL，ER分别为左旋圆极化分量场和右旋圆极化分量场的幅度；φc为两分量场的初始相位差。为方便说明，两坐标基取x，y，上述公式可化为

E(t)=x[ELcos(wt)+ERcos(wt+φc)]+

y[-ELsin(wt)+ERsin(wt+φc)].

根据式中幅度和相位的关系，可分为3种情况：

(1) 当EL=ER=Ec时，合成场为线极化波，根据三角函数公式，可得其瞬时幅度为E(t)=2Ec|cos(wt+φc/2)|，极化方向与x夹角θ为一常数θ=φc/2。

(2) 当EL或ER接近为0时，合成场为圆极化波，左旋圆极化为E(t)=EL[cos(wt)x-sin(wt)y]，右旋圆极化为E(t)=ER[cos(wt+φc)·x+sin(wt+φc)y]。

1.3 两种分解方法之间联系与实际应用

用线极化天线测量线极化天线，圆极化天线测量圆极化天线是最理想的测试方法，但实际中很难找到纯圆极化天线，所以大多数情况下，针对圆极化天线的测试仍是采用分解为两线极化分量的方法[12-14]。用一个高纯度的线极化辅助天线，分别在辅助天线极化处于水平和垂直时，测量得到每一个截面中每个测量角上天线的远场幅相(HA,HP)，(VA,VP)代入公式

j[HAsinHP-VAcosVP]}，

j[HAsinHP+VAcosVP]}，

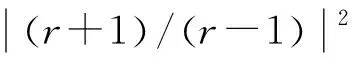
2 极化失配理论分析

2.1 来波信号与接收天线均为任意线极化

设来波信号两正交极化分量幅度比值为ρ1，相位差为φ1，设接收天线两正交极化分量比值为ρ2，相位差为φ2。极化失配因子表达式为

当来波信号与接收天线均为线极化时，ρ1，ρ2取值任意，φ1，φ2取值为0或π。式(5)可化为

取来波信号极化倾角θ1分别为0,π/6,π/3,π/2，绘制极化失配因子与接收天线极化倾角θ2的关系图如图1所示。

从图1中可知，两极化倾角相差0或π时，极化失配因子为1，接收天线与来波信号完全匹配，接收机获得最大接收功率；当两极化倾角相差π/2时，极化失配因子为0，接收天线与来波信号完全失配，接收系统获得功率为0；在其他情况下，极化失配因子0<ρ<1，接收机接收功率有损耗。

2.2 来波信号与接收天线均为任意椭圆极化

收发天线均为椭圆极化的情况，分别设两椭圆极化轴比为r1，r2，两天线极化椭圆长轴夹角为Δθ，极化失配因子可化为

图2给出了极化失配因子随接收天线轴比的变化曲线(以Δθ=0，长轴取垂直轴为例)。从图2中可看出，当接收天线与来波旋向相同且轴比为0时，接收天线与来波信号完全匹配，极化失配因子为1，雷达接收机获得最大接收功率。随着轴比的增加，极化失配因子减小，接收机接收功率降低，当轴比趋于无限大时，接收天线趋于线极化，极化失配因子为0.5，接收功率下降3 dB；反之，当接收天线与来波旋向相反时完全失配，极化失配因子为0，雷达接收不到信号，随着轴比的增加，接收机接收功率增加。当用圆极化天线接收线极化波时，当轴比为0时极化失配因子为0.50，当接收天线轴比取3 dB，来波为垂直线极化时，可知极化失配因子近似为0.67。

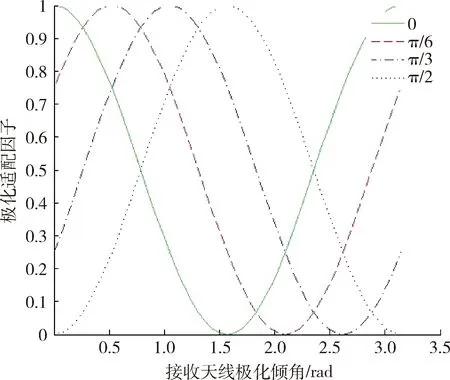
图1 极化失配因子随来波信号与接收天线 极化倾角变化仿真图Fig.1 Simulated diagram of polarization mismatch factor change with variation of the polarization angle of receiving antenna

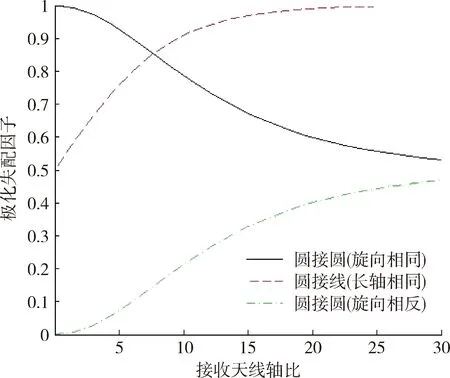
图2 极化失配因子随接收天线轴比变化仿真图Fig.2 Simulated diagram of polarization mismatch factor change with variation of the axial ratio of receiving antenna

3 极化在雷达对抗中的影响分析

3.1 对干扰机接收机灵敏度影响

干扰机接收机灵敏度计算公式为

式中：Pt为雷达峰值功率；Gt为雷达天线增益；λ为波长；Lt为雷达发射损耗；Ljr为干扰机接收损耗；Rj max为干扰机最远工作距离；Gjr为干扰机接收天线完全匹配时最大辐射方向上增益[15-16]。接收天线的圆极化性能(轴比)影响了干扰机接收天线实际增益，雷达发射天线与干扰机接收天线的极化失配影响干扰机接收损耗Ljr，最终影响干扰机接收机灵敏度。

3.2 对雷达接收信号干信比影响

(1) 对于恒功率干扰机

雷达接收目标回波功率为

式中：Rs为目标距离；σ为目标雷达散射截面积；Lt为雷达发射损耗；Lr为雷达接收损耗。

雷达接收到的干扰功率为

式中：Pj为干扰机发射功率；Gjt为干扰机发射天线增益；Ljt为干扰机发射损耗；Rj为干扰距离。

上述两式相除可以得到干信比为

干扰机发射天线的圆极化性能(轴比)影响了干扰机接收发射天线实际增益，雷达接收天线与干扰机发射天线的极化失配影响干扰机发射损耗Ljt，最终影响雷达接收信号干信比。

(2) 对于恒增益干扰机

干扰机接收到雷达的信号功率为

设干扰机系统增益为Gj，雷达接收到的干扰功率为

雷达接收信号的干信比

干扰机接收天线、发射天线的圆极化性能(轴比)影响了干扰机收发天线总的实际增益，雷达天线与干扰机天线的极化失配影响干扰机收发总损耗LjtLjr，最终影响雷达接收信号干信比。

4 结束语

本文以雷达极化学理论为基础，研究了雷达天线的空域极化特性，分析了任意极化波的合成与分解。并在雷达对抗领域，针对不同极化的收发系统，给出了极化失配因子对接收机灵敏度及雷达接收端干信比的影响，对研究雷达天线及雷达对抗试验有一定的参考意义。