一种雷达导引头天线罩斜率误差实时估计方法
周荻,李君龙,袁宇祺
(1.哈尔滨工业大学 控制工程系,黑龙江 哈尔滨 150001;2.北京电子工程总体所,北京 100854)
0 引言
导引头天线罩对电磁波的折射和反射作用影响导引头天线的测量精度,使其指向一个虚假的目标方向,造成瞄准误差,引起导弹脱靶增加。
李瑞等人[1]通过对控制系统的合理简化,提出了一种基于比例导引律的导引头天线罩瞄准线误差斜率的简化计算方法。祁琪等人[2]建立了基于抖动信号的天线罩误差估计模型。顾炳良[3]运用二维射线轨迹法计算了天线罩的瞄准线误差和传输系数。Zarchan等[4]利用无损高频抖动信号来估计和补偿瞄准线误差。Rong等人[5]基于平面波谱曲面积分数字仿真的方法来计算瞄准线误差。陈意芬等人[6]通过遗传算法寻找一个导引控制器。缪雪佳等人[7]提出了一种负反馈偏置的补偿方法,在导引头输出处加上一个与天线罩误差斜率相关的正的弹体姿态角速率信号,以减弱正反馈的影响。曾宪伟等[8]建立了视线角速度估计模型,提出了一种天线罩误差斜率修正的视线角速度估计算法。刘元云[9]、居加祥[10-11]等人选择寻零法测试天线罩的电性能,采用分段二阶线性拟合的方法得到天线罩误差补偿模型。刘军等人[12]介绍了一种基于DSP处理器的导弹天线罩瞄准线误差补偿系统。Yueh[13]提出了一个带有内部学习程序的卡尔曼滤波器组合。Lin等[14]通过引入带通滤波器机制来预测天线罩误差,并在导弹制导回路中加入无损高频抖动信号来对误差进行补偿。安相宇等人[15]提出了一种基于推广卡尔曼滤波的方法估计天线罩误差斜率。Gurfil等[16]则把两步滤波方法应用于天线罩误差斜率估计问题。Han S K[17]、Lin[18]等人利用交互式多模型卡尔曼滤波方式估计天线罩误差。宗睿[19-20]基于极点配置自校正理论提出了一种天线罩寄生回路的在线补偿方法。
本文提出在极坐标系中建立精确的目标-导弹相对运动模型和测量模型,采用推广Kalman滤波器对天线罩误差斜率和视线角速率进行联合估计,从而获得较高的制导精度。
1 考虑导引头天线罩误差斜率的目标-导弹相对运动问题数学描述
1.1 考虑导引头天线罩误差斜率的相对运动问题三通道数学描述
1.1.1 目标-导弹相对运动模型
目标-导弹视线运动动力学方程投影到视线坐标系可以表示为[21]
(1)
式中:r为目标-导弹相对距离;qε为视线俯仰角,表示视线(Ox4轴)与惯性参考系侧向平面Oxz之间的夹角。若视线在侧向平面之上,则qε为正,反之为负;qβ为视线偏航角,表示视线在惯性参考系侧向平面Oxz上的投影与Ox轴之间的夹角。迎Oy轴顶视,若Ox轴逆时针转到投影线上,则qβ为正,反之为负;ar,aε和aβ分别为导弹加速度在视线坐标系3个轴上的分量,可以用惯导系统测量得到;atr,atε和atβ分别为目标加速度在视线坐标系3个轴上的分量。针对固定目标,atr=0,atε=0,atβ=0。
1.1.2 导引头测量模型

(2)
(3)
式中:C0→4为从惯性系到视线系的转换矩阵。
根据各坐标系之间的转换关系
(4)
式中:C0→1为从惯性系到弹体系的转换矩阵。
视线相对于弹体系所成的角度可表示为
Δqε=arcsinc1y=arcsin[C0→1(2,1)cosqεcosqβ+
C0→1(2,2)sinqε-C0→1(2,3)cosqεsinqβ],
(5)
(6)
在考虑导引头天线罩斜率误差的情况下,导引头测量的视线相对于弹体系所成的角度可以描述为
Δqε=(1+bε)arcsin[C0→1(2,1)cosqεcosqβ+
C0→1(2,2)sinqε-C0→1(2,3)cosqεsinqβ],
(7)
(8)
式中:bε和bβ分别为俯仰通道和偏航通道的天线罩瞄准误差斜率。
在实际飞行中,由于环境因素的影响,天线罩瞄准误差斜率是随机变化的,所以将其变化过程视为随机高斯白噪声,即
(9)
(10)
式中:wε和wβ分别为导引头测量机构俯仰通道和偏航通道的高斯白噪声。
1.1.3 状态方程
状态方程包括以下内容:
(11)
(12)
1.1.4 测量方程
导引头的测量量为r,Δqε和Δqβ,考虑式(8)和(9),测量方程写作
(13)
1.2 纵向通道考虑天线罩误差斜率的目标-导弹相对运动问题数学描述
1.2.1 纵向通道考虑天线罩误差斜率的目标-导弹相对运动数学模型
由完整的数学模型(12)和(13),忽略式(12)中偏航通道状态量x7对俯仰通道的影响,可得仰通道的状态方程为
(14)
测量方程为
(15)
式中:qβ视作外来的已知量。
如果忽略侧向通道的视线运动和姿态运动,即假设qβ,ψ和γ均约等于0,则俯仰通道测量方程可以简化为
(16)
1.2.2 纵向通道联合估计视线角速率和天线罩误差斜率的数学模型
对俯仰通道考虑天线罩误差斜率的目标-导弹相对运动数学模型(14)和(15)进一步做简化处理。
(17)
测量方程降低到1维,即只有角度测量信息:
y1=(1+x3)arcsin[C0→1(2,1)cosx1cosqβ+
C0→1(2,2)sinx1-C0→1(2,3)cosx1sinqβ],
(18)
而在忽略侧向通道的视线运动和姿态运动,即假设qβ,ψ和γ均约等于0的情况下,式(18)简化为
y1=(1+x3)(x1-ϑ).
(19)
2 天线罩误差斜率及视线角速率联合估计问题的可观性分析
2.1 非线性状态模型可观性分析
首先,研究俯仰通道考虑天线罩误差斜率的目标-导弹相对运动数学模型和所构成的观测系统的可观性。
经验证,该矩阵秩为5,所以该系统可观。
2.2 线性时变状态模型可观性分析
由公式(17)和(19)观测系统的可观性模型。
(20)
经验证,该矩阵秩为3,所以系统可观。
3 天线罩误差斜率及视线角速率联合估计推广Kalman滤波器设计
3.1 纵向通道联合估计视线角速率和天线罩误差斜率Kalman滤波器
(21)

令状态向量Xε=[x1x2x3]T,uε=aε。将式(2)这一线性时变系统离散化后得到
Xε(k+1)=Φε(k)Xε(k)+Βε(k)uε(k),
其中,
由于模型误差等原因,在上式中加入一个零均值高斯随机过程向量ηε(k),得到
Xε(k+1)=Φε(k)Xε(k)+Βε(k)uε(k)+ηε(k).
(22)
测量方程取导引头测量得到的视线相对弹体系所成的角度:
y1=(1+x3)arcsin[C0→1(2,1)cosx1cosqβ+
C0→1(2,2)sinx1-
C0→1(2,3)cosx1sinqβ]+υ(k),
(23)
式中:υ(k)为一个零均值高斯随机过程。
将式(23)这个非线性测量方程写作
yε(k)=h(Xε(k))+υ(k).
(24)
式中:
h(Xε(k))=(1+x3)arcsin[C0→1(2,1)cosx1cosqβ+
C0→1(2,2)sinx1-
C0→1(2,3)cosx1sinqβ].
(25)
又设
(26)
(27)
设计俯仰通道推广Kalman滤波器为
(28)


(29)
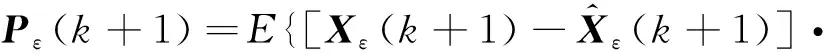
(30)
3.2 侧向通道联合估计视线角速率和天线罩误差斜率Kalman滤波器设计

(31)
(32)
(33)
(34)
而导引头天线罩误差斜率的初始估计值取bε=0。
4 天线罩误差斜率及视线角速率联合估计问题的数学仿真
4.1 仿真条件
考察1条对地攻击导弹的末制导飞行弹道。末制导初始时刻(t0=120 s)导弹在惯性系中的初始位置x,y,z,速度vx,vy,vz,俯仰角ϑ,偏航角ψ,滚转角γ,以及姿态角速度ωx,ωy,ωz如表1所示。

表1 末制导初始时刻导弹状态Table 1 Missile status at the initial instant of terminal guidance
导弹惯导系统的数据更新周期为2.5 ms,控制周期为2.5 ms,惯导系统的3个初始姿态角误差分别用均方根为0.05°的高斯白噪声描述,惯导系统的初始速度在惯性参考系中的3个分量的误差用在-0.2~0.2 m/s之间均匀分布的白噪声描述,加速度计的误差用标准差为4×10-5g的零均值高斯白噪声描述。
导引头采样周期为20 ms,测距误差用σ=3 m的零均值高斯白噪声描述,纵向和侧向测角随机误差均用σ=0.103 125°的零均值高斯白噪声描述。导引头高低测量通道和方位测量通道均有天线罩斜率误差。在仿真过程中的具体变化情况在后面的仿真结果图中提供。
4.2 仅采用视线角速率估计Kalman滤波器无天线罩误差补偿的仿真结果
纵向和侧向通道状态估计方差阵的初值取为Pε(k)=diag[0.1 0.1],Pβ(k)=diag[0.1 0.1],估量测噪声方差取为Rε(k)=0.015,Rβ(k)=0.015。动态噪声方差阵取为Qε(k)=diag[0 10-3],Qβ(k)=diag[0 10-3]。
在2个通道中均加入了天线罩斜率误差(radom slope error,RSE)。由于天线罩斜率误差的影响,制导滤波器乃至整个制导控制系统工作并不理想,最终脱靶量为19.767 m。飞行弹道如图 1所示。图2显示了Kalman滤波器估计出来的视线角速率明显振荡,这种带振荡的估计值代入到制导律后导致导弹过载制导指令的振荡和导弹过载的振荡(见图3),进而又导致了视线角速率真实值的振荡(见图2)。所以,在图2中,视线角速率真实值的振荡滞后于视线角速率估计值的振荡。
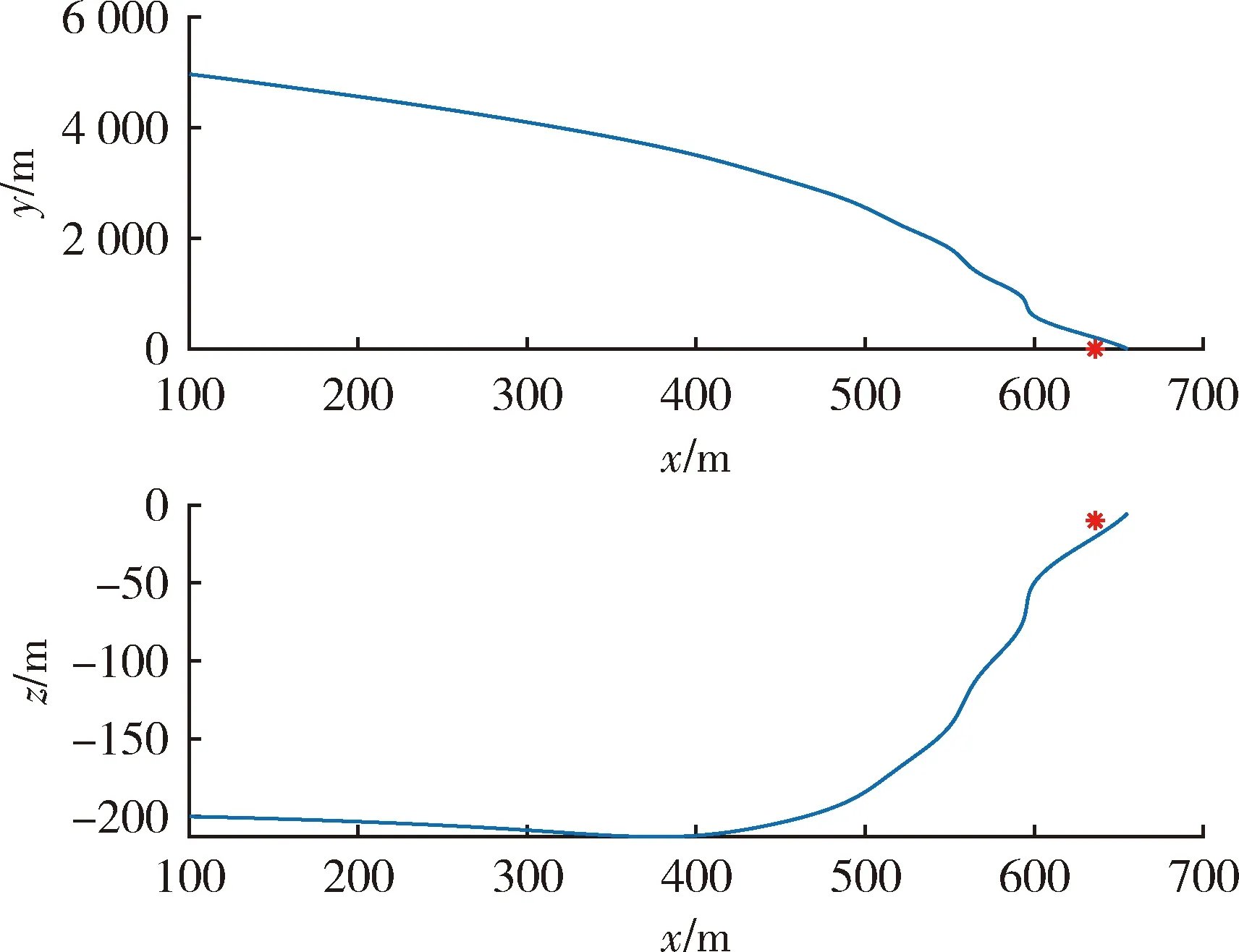
图1 飞行弹道(无天线罩斜率误差估计)Fig.1 Flight trajectory (without estimation for RSE)
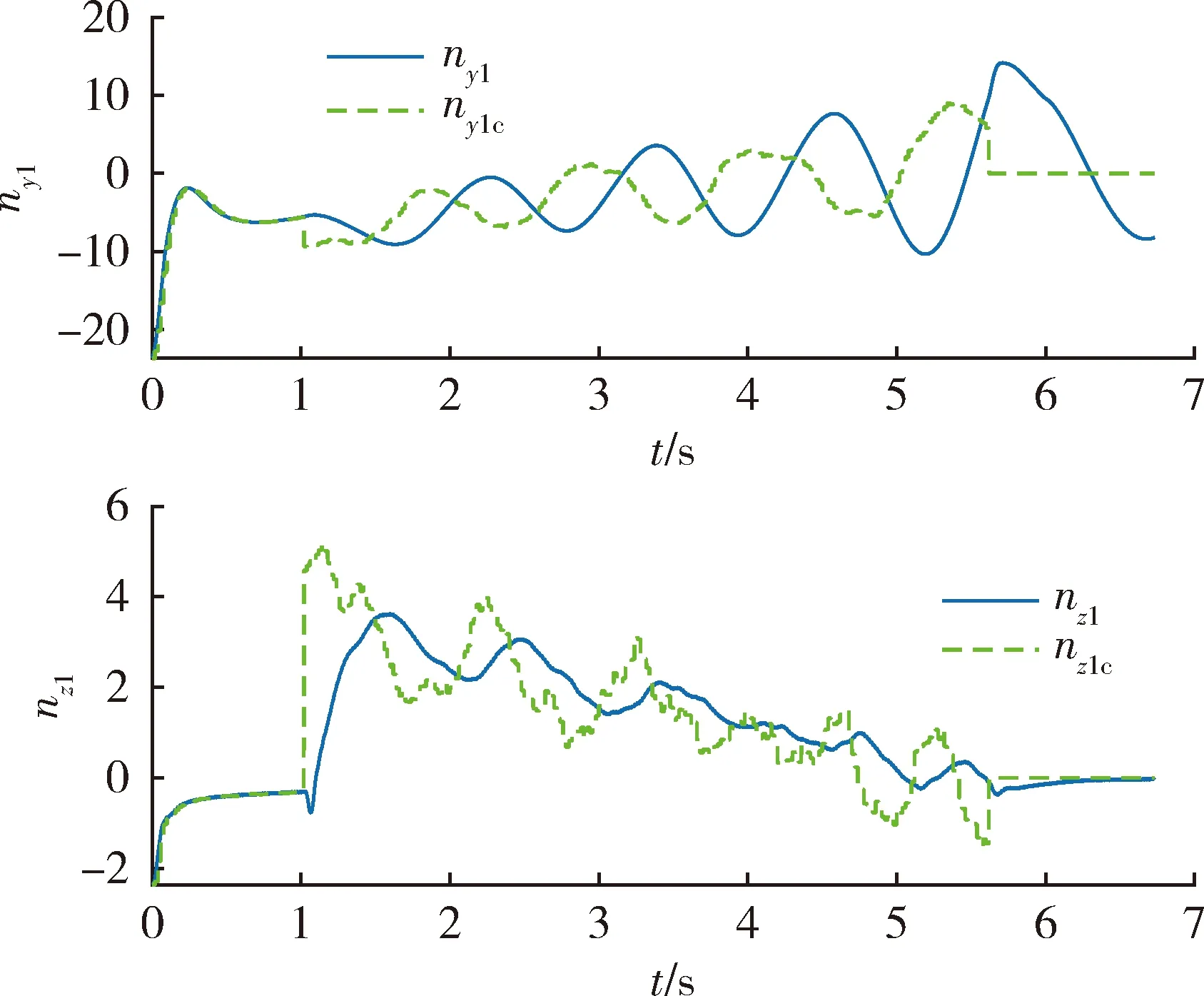
图3 导弹法向过载(无天线罩斜率误差估计)Fig.3 Normal acceleration of missile (without estimation for RSE)
从图4可以看出天线罩斜率误差的真实值变化很剧烈,而Kalman估计值为0代表未对该误差进行补偿。所以,制导控制系统工作性能不理想。

图4 天线罩斜率误差的真实值和估计值 (无天线罩斜率误差估计)Fig.4 True and estimated values for radome slope error (without estimation for RSE)
4.3 视线角速率与天线罩误差斜率联合估计Kalman滤波器仿真结果
在同样条件的制导控制系统仿真中,纵向通道和侧向通道均采用视线角速率与天线罩误差斜率联合估计Kalman滤波器。
状态估计方差阵的初值取为
估量测噪声方差取为Rε(k)=0.015,Rβ(k)=0.015;动态噪声方差阵取为
由于联合估计视线角速率和天线罩斜率误差,制导滤波器工作性能明显提高,整个制导控制系统工作性能良好,制导精度明显上升,终端脱靶量只有1.184 9 m。飞行弹道如图5所示。
联合估计后,图6显示的联合滤波器估计出来的视线高低角速率和视线方位角速率很好地跟踪了视线高低角速率和视线方位角速率的真实值。从图7看出,2个通道中天线罩斜率误差的估计值的基本趋势可以跟踪真实值的变化情况,虽然它们不一定十分准确地跟上真实值,但却明显改善了联合滤波器对视线角速率的估计精度(见图6)。从图8 看出纵向通道和侧向通道过载指令跟踪效果均很好。上述结果表明,使用联合估计滤波器后,制导控制系统的性能明显改进了。

图5 飞行弹道(有天线罩斜率误差估计)Fig.5 Flight trajectory (with estimation for RES)

图7 天线罩斜率误差的真实值和估计值 (有天线罩斜率误差估计)Fig.7 True and estimated values of radome slope error (with estimation for RSE)
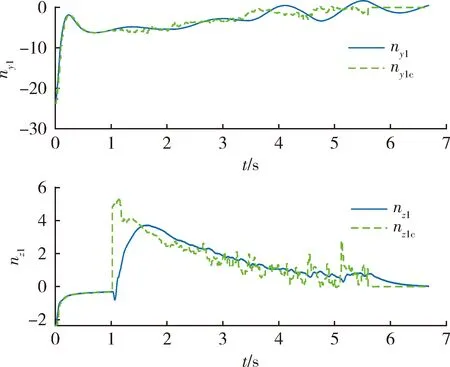
图8 导弹法向过载(有天线罩斜率误差估计)Fig.8 Normal acceleration of missile (with estimation for RES)
4.4 Monte-Carlo仿真对比
在前面所述条件下,将仅采用视线角速率估计Kalman滤波器的制导控制系统与采用视线角速率与天线罩误差斜率联合估计Kalman滤波器的制导控制系统进行100次Monte-Carlo仿真对比。仿真结果表明,仅采用视线角速率估计Kalman滤波器的制导控制系统受天线罩误差斜率的影响很大,脱靶量CEP值达到20.29 m,而采用视线角速率与天线罩误差斜率联合估计Kalman滤波器的制导控制系统很好地克服了天线罩误差斜率的影响,脱靶量CEP值3.13 m。
5 结束语
本文首先建立了完整的考虑导引头天线罩误差斜率的目标-导弹相对运动问题数学描述,包括非线性的状态方程和测量方程。然后,简化得到俯仰通道考虑天线罩误差斜率的目标-导弹相对运动数学模型,又进一步推导出俯仰通道联合估计视线角速率和天线罩误差斜率的数学模型。应用非线性系统可观性理论,证明了上述数学模型对应的视线角速率和天线罩误差斜率联合观测系统的可观性。
在上述分析的基础上,设计了联合估计视线角速率和天线罩误差斜率的推广Kalman滤波器。在某对地攻击导弹末制导段全弹道制导控制系统仿真中,应用该滤波器进行仿真,并与不考虑天线罩误差斜率的视线角速率估计Kalman滤波器做了仿真对比。仿真结果表明,联合估计视线角速率和天线罩误差斜率的推广Kalman滤波器的效果很好,可以显著提高天线罩误差斜率情况下的制导精度。

