高超声速飞行器平衡滑翔状态变量的求解
孟繁卿,田康生
(空军预警学院a.研究生大队;b.四系,湖北 武汉 430019)
0 引言
高超声速飞行器是一种具备颠覆性的新型武器运载平台,不仅具备超远距离投送能力,而且飞行速度为高超声速、弹道轨迹灵活多变。当前的各种导弹防御系统在面对高超声速飞行器时,尚难以实现有效拦截,高超声速飞行器因此被视为改变战争规则的杀手锏武器[1]。高超声速滑翔飞行器作为高超声速飞行器的一种,通过火箭助推或天基平台释放到达一定高度后进入滑翔状态。其在滑翔段借助空气动力实现滑翔飞行,飞行速度Ma大于5,飞行高度大于20 km。
文献[2]通过对飞行器运动方程无量纲化和规范化,在对运动方程简化的基础上利用解析积分求得了状态变量的一阶解析解,进一步利用解析延拓方法求得了状态变量的二阶解析解。文献[3]利用解析积分求得了飞行器滑翔段射程的近似解析式,提出并证明了采用最大升阻比平衡滑翔可获得最大射程的结论。文献[4]利用谱分解的方法求解了平衡滑翔横向航程、纵向航程和方位角的解析解,基于所求解析解设计的再入制导律,能满足多种任务需求,且对初始状态误差不敏感。文献[5]采用正则摄动的方法求解了平衡滑翔高度、速度倾角和纵向加速度的解析解,利用所求解析解设计了一种控制平滑、弹道收敛快,且具有良好鲁棒性的平衡滑翔方案。文献[6]在常升阻比条件下,通过查找有理函数积分表,求解了射程、飞行高度和速度之间的关系式,分析了不同初始状态时的弹道特性。文献[7]利用平衡滑翔条件求解了飞行器射程的解析解,分析了升阻比、初始状态等参数对弹道射程的影响,从能量的角度提出了弹道方案的选择方法。
通过对以上文献的分析可知,对飞行器运动规律,即飞行器状态变化规律的分析至关重要[8-9]。为此,本文对高超声速滑翔飞行器在纵向平衡滑翔情况下,飞行器状态变量的解析表达式进行了求解分析,以期为目标跟踪模型构建、弹道轨迹预测、弹道特性分析、目标预警探测等提供参考。
1 高超声速滑翔飞行器运动模型
根据高超声速滑翔飞行器在滑翔段的受力情况,建立其运动方程[10-11]:
(1)
式中:v为飞行速度;γ为速度倾角;(x,z)为飞行器的位置坐标;m为飞行器质量;g0为重力加速度常数;L为飞行器所受升力;D为飞行器所受阻力。
其中升力、阻力的计算可由式(2)求得
(2)
式中:S为飞行器的参考面积;CL为飞行器的升力系数;CD为飞行器的阻力系数[12];ρ为大气密度,如式(3)所示:
ρ(z)=ρ0ez/ξ,
(3)
在此采用指数模型计算飞行器所在高度的大气密度,ρ0为海平面大气密度常数1.225 kg/m3;ξ为归一化高度常数8 434 m;R0为地球平均半径,取为6 371 km。
纵向平衡滑翔是飞行器在纵向平面受力平衡,需要满足平衡滑翔条件[13-14]:
(4)
飞行终端约束式为
Ω={(xf,zf)||zf|≥hf,|xf-xt|≤df},
(5)
式中:(xf,zf)为滑翔段结束时刻飞行器的位置坐标;xt为目标点横坐标;hf为终端高度约束;df为滑翔段结束时刻飞行器与目标点的距离约束。
2 飞行器状态变量数值解
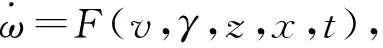
(6)
式中:ti=t0+iΔt,(i=0,1,2,…);Δt为迭代时间步长。
3 平衡滑翔状态变量求解
3.1 飞行速度、纵程和高度
由平衡滑翔条件式(4)可得
(7)
所以可推导出飞行速度表达式为
(8)
式(8)对z求微分可得
(9)
又因为
(10)
将式(1)代入式(10)可得
(11)
由式(7),(9)和式(11)可得
(12)
又因为
(13)
将式(1)代入式(13)可得
(14)
将式(2)代入式(14)可得
(15)
将式(7)代入式(15)可得
(16)
对式(16)整理可得
(17)
将式(12)代入式(17)整理可得
(18)
对式(18)积分可得
(19)
式(19)中Cx为常数,将式(12)代入式(19)可得飞行纵程x的解析式:
(20)
由式(8)和式(12)可得
(21)
对式(21)整理可得
(22)
由式(3)和式(22)可得z的解析式为
(23)
3.2 速度倾角
因为平衡滑翔弹道需满足平衡滑翔条件,速度倾角变化率为0,且文献[16]已证明速度倾角为负的小量,所以无法通过理论推导求出速度倾角的解析表达式。为了求解速度倾角的近似解,通过龙格-库塔求得速度倾角的数值解,利用正交多项式拟合速度倾角的数值解[17]。分别采用1,2,3阶正交多项式拟合速度倾角的数值解,拟合函数分别如式(24)~(26)所示,P0(t),P1(t),P2(t),P3(t)为拟合函数的基函数,其中Pj(t),(j=0,1,2,3)是关于t的j次正交多项式。
γ(t)=d0P0(t)+d1P1(t),
(24)
γ(t)=d0P0(t)+d1P1(t)+d2P2(t),
(25)
γ(t)=d0P0(t)+d1P1(t)+d2P2(t)+d3P3(t).
(26)
(27)
(28)
3.3 仿真校验及分析
为验证平衡滑翔条件下所求状态变量解的正确性,以美国洛克希德·马丁公司研发的高超声速通用气动飞行器CAV-H(common aero vehicle)为例[18]。取目标点位置(4 000×103,-100),飞行器以最大升阻比攻角α=12°飞行,hf=20 km,df=200 km。其滑翔段初始状态为,v0=6 078.383 m/s,γ0=-0.085 7°,x0=0,z0=-54.006×103。
如图1所示为速度倾角数值解与近似解,图2为不同阶次近似解的RMSE。由图2可知,速度倾角的一阶近似解存在较大误差,说明平衡滑翔条件下速度倾角与飞行时间不满足线性关系。二阶近似解和三阶近似解均能很好的表征速度倾角的变化规律,但三阶近似解的精度更高。
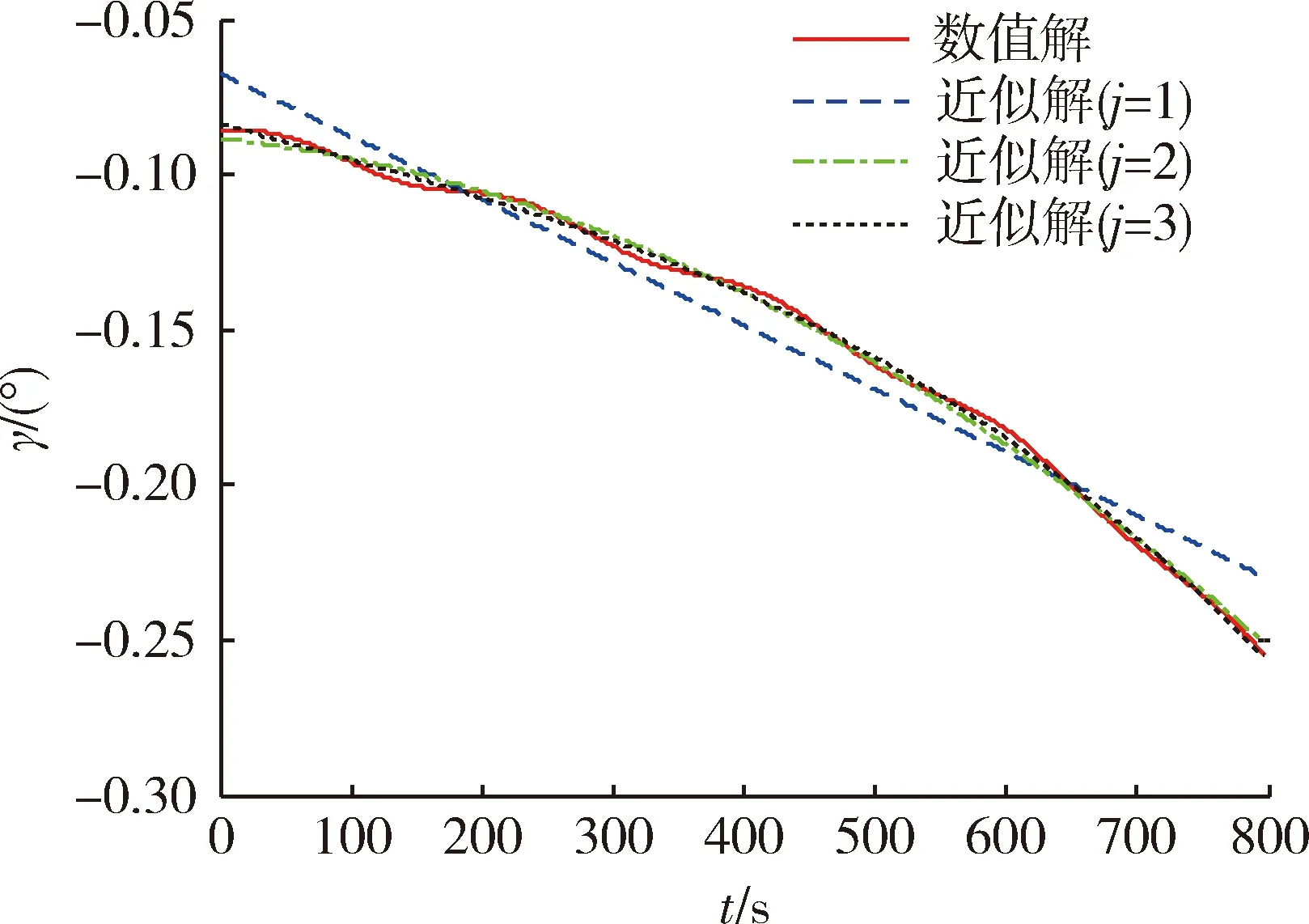
图1 速度倾角数值解与近似解Fig.1 Numerical and approximate solution of flight path angle
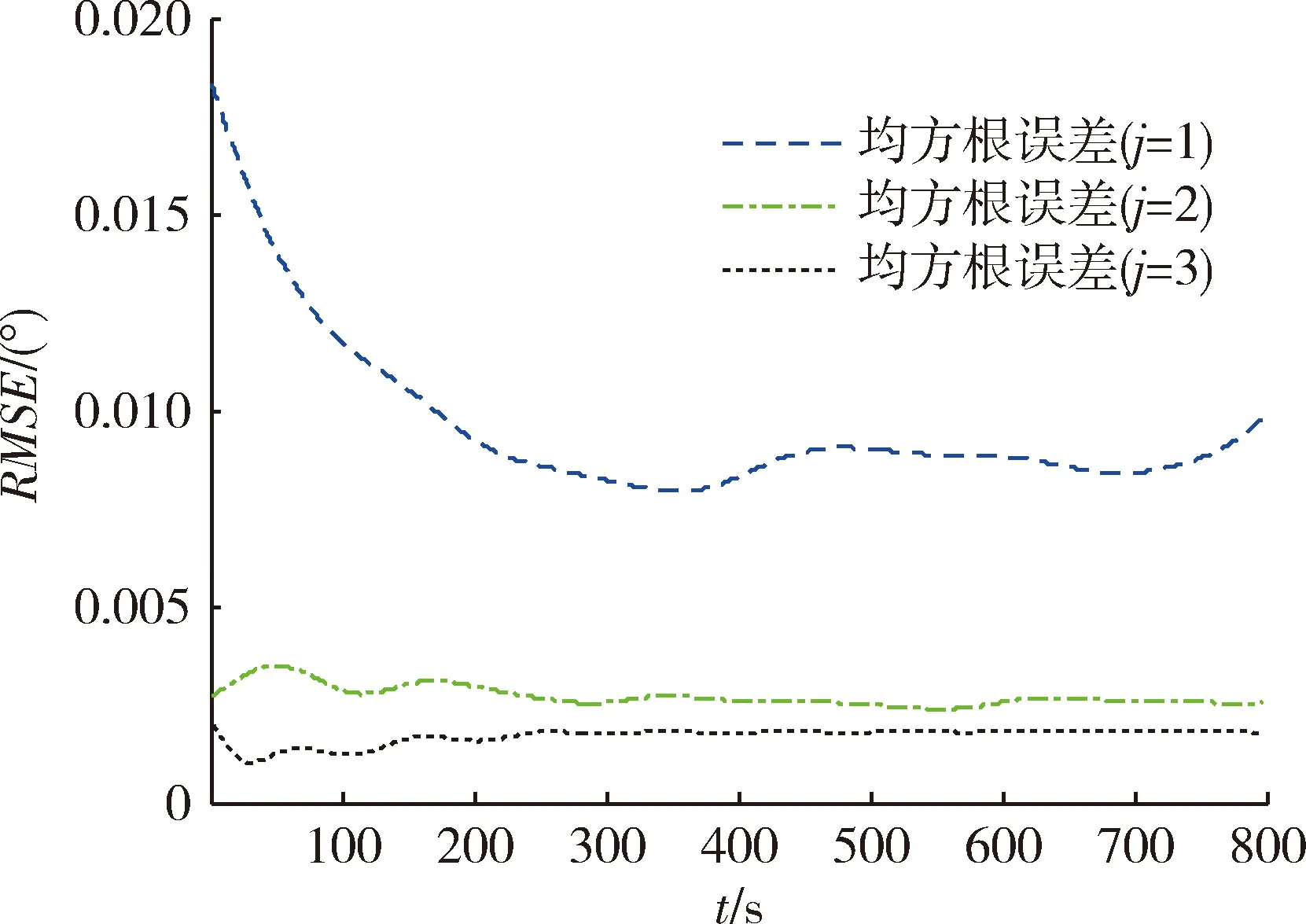
图2 速度倾角近似解的RMSEFig.2 Approximate solution RMSE of flight path angle
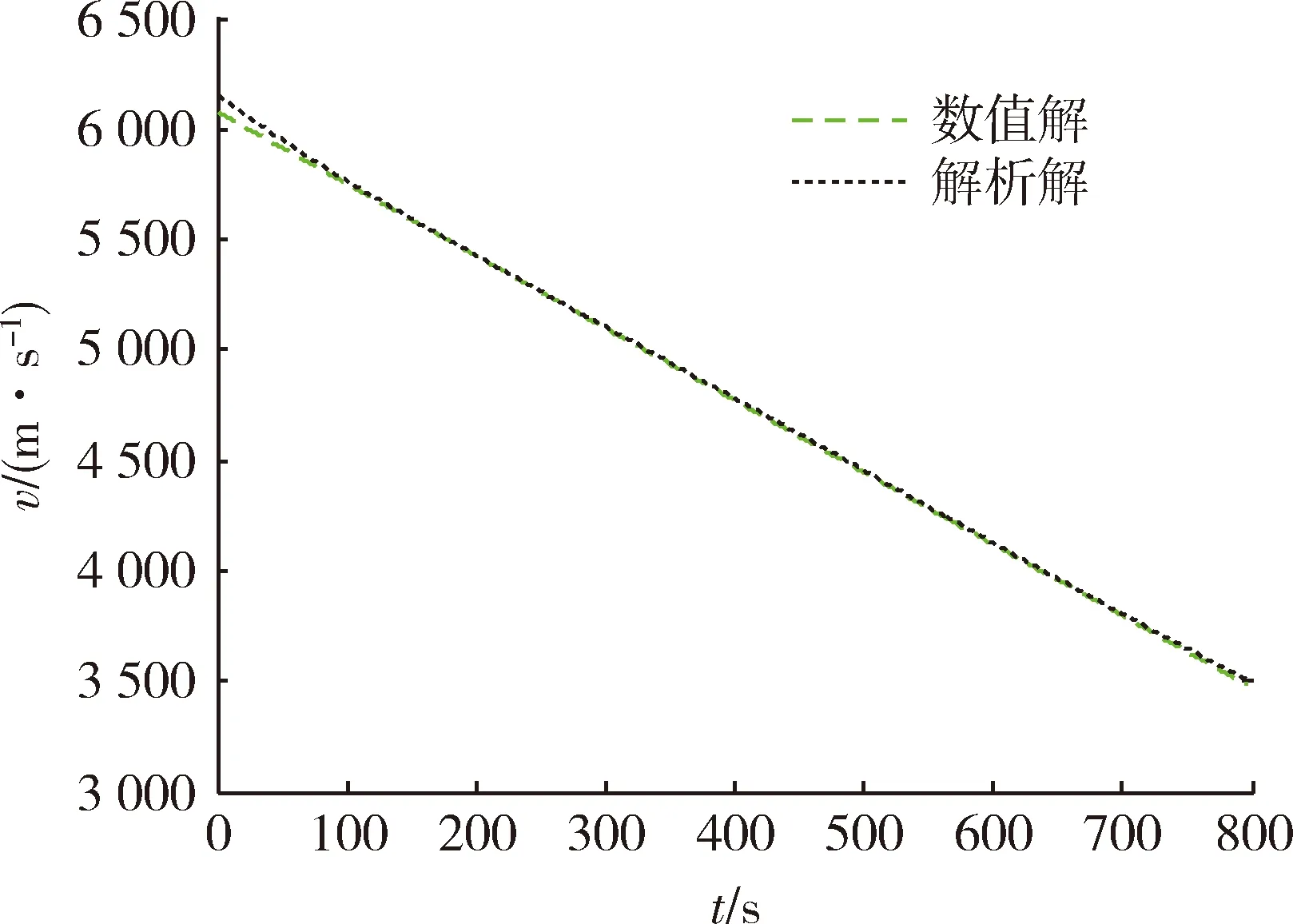
图3 飞行速度数值解与解析解Fig.3 Numerical and analytical solution of flight speed
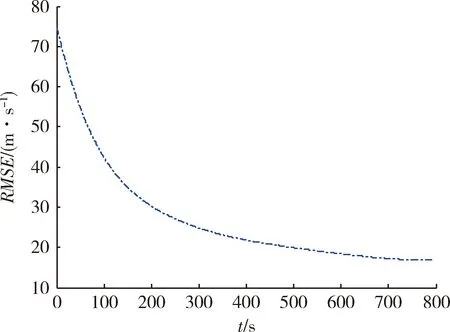
图4 飞行速度解析解的RMSEFig.4 Analytical solution RMSE of flight speed
将速度倾角的三阶近似解分别代入式(12),(19),(23),可得到飞行速度、纵程及高度的解析解。图3为飞行速度数值解与解析解,图4为飞行速度解析解的RMSE。图5为飞行纵程数值解与解析解,图6为飞行纵程解析解的RMSE。图7为飞行高度数值解与解析解,图8为飞行高度解析解的RMSE。由图4,6,8可知,飞行速度解析解的RMSE最大不超过80 m/s,在滑翔段结束时解析解的RMSE小于20 m/s;飞行纵程解析解的RMSE最大不超过140 km,在滑翔段结束时解析解的RMSE约为30 km;飞行高度解析解的RMSE最大不超过220 m,在滑翔段结束时解析解的RMSE小于50 m。由以上分析可知,飞行速度、纵程、高度的解析解均能以较高精度表征相应状态变量的数值解。
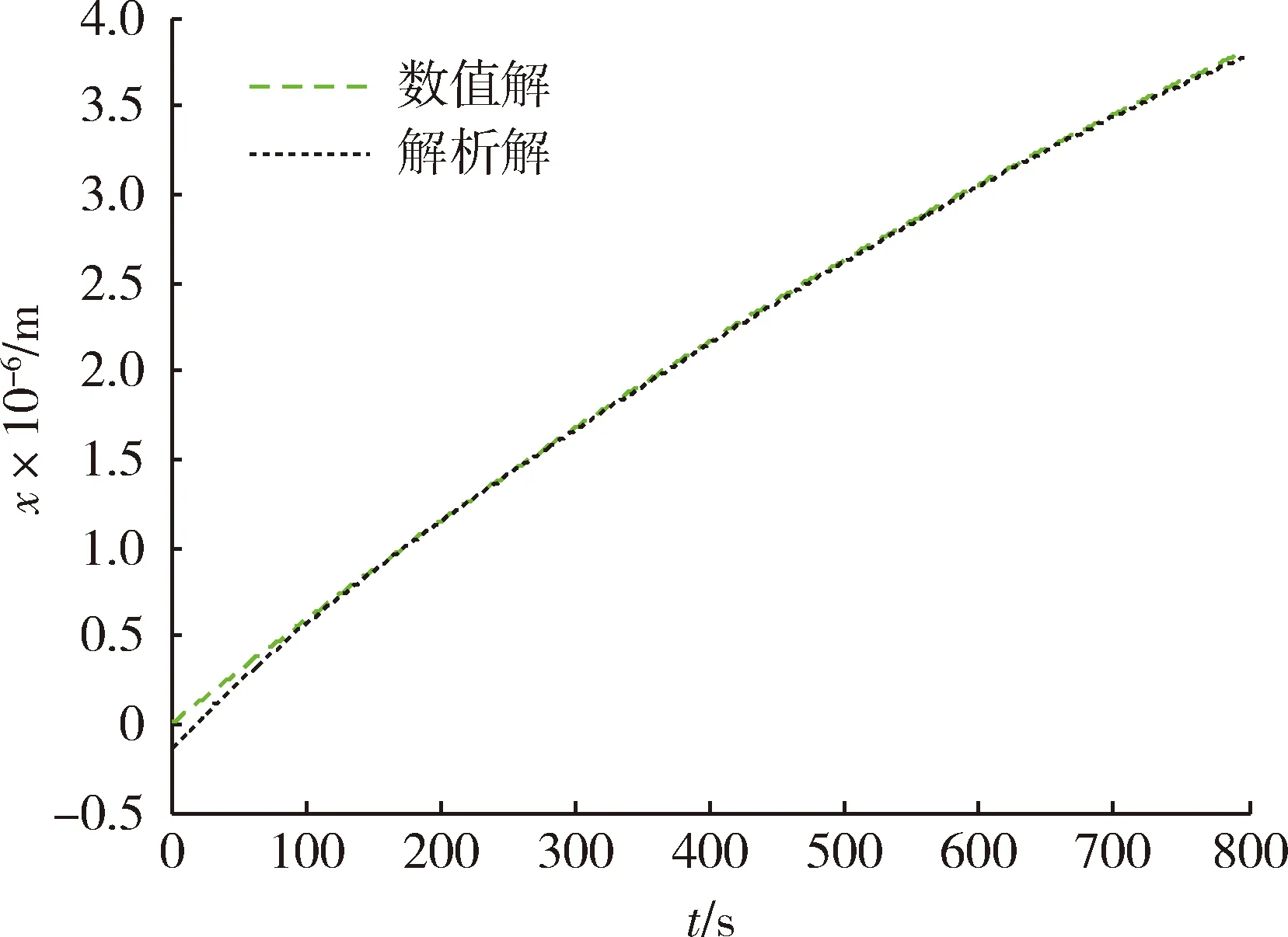
图5 飞行纵程数值解与解析解Fig.5 Numerical and analytical solution of longitudinal range
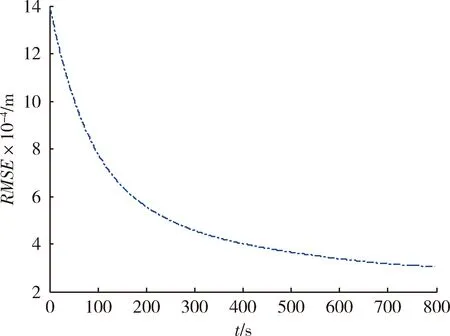
图6 飞行纵程解析解的RMSEFig.6 Analytical solution RMSE of longitudinal range

图7 飞行高度数值解与解析解Fig.7 Numerical and analytical solution of flight altitude
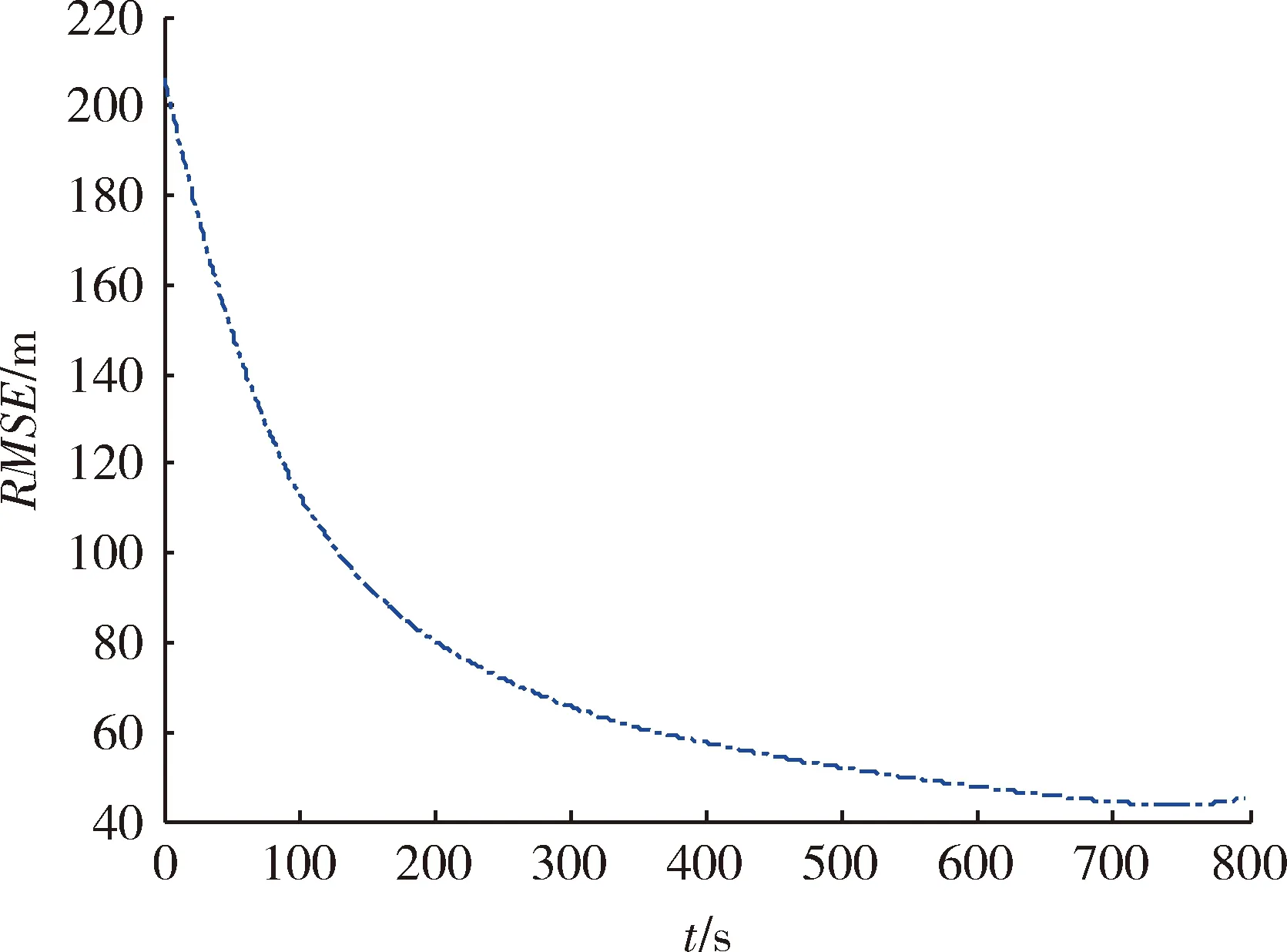
图8 飞行高度解析解的RMSEFig.8 Analytical solution RMSE of flight altitude
4 结束语
针对高超声速滑翔飞行器滑翔段状态变量的求解问题,理论推导了平衡滑翔条件下飞行速度、飞行纵程、飞行高度的解析式,利用曲线拟合得到的速度倾角三阶近似解的平均RMSE不大于0.003°。由仿真结果,可得到如下结论:
平衡滑翔条件下,速度倾角-飞行时间呈现非线性关系,利用二阶或三阶正交多项式均能很好的拟合速度倾角的数值解,三阶近似解精度比二阶近似解高0.001°左右。在得到速度倾角近似解的基础上,飞行速度、飞行纵程和飞行高度的解析解都能以较高精度表征相应状态变量的数值解。在滑翔段结束时,飞行速度解析解的RMSE小于20 m/s,飞行纵程解析解的RMSE约为30 km,飞行高度解析解的RMSE小于50 m。

