以皓骏设计“三角形内接矩形面积的最值问题”的积件及教学应用

李 莉 张祥婕 唐海明

（[1]广西师范大学 广西·桂林 541006；[2]桂林市雁山中学 广西·桂林 541004）

“三角形内接矩形是指四个顶点都在三角形的边上的矩形。而求三角形内接矩形的最值”是最值问题中的经典范例。此类问题综合考察了相似三角形的性质、二次函数性质、矩形的性质，更为学生建立最值问题转化为函数的最值问题的模型思想巩固基础，更是培养学生几何直观、逻辑推理、数学建模等数学核心素养的重要载体。本节课的重难点是函数最值问题的模型建立。在传统“粉笔+黑板”的课堂中，主要是板书作图和语言直观，操作繁琐、不具一般性及推广性，且难以展现矩形面积随其边长变化的动态过程，更难以展现从具体的三角推广到任意的、一般的三角形内接矩形面积最值以及其他图形内接矩形最值问题。本文将以Hawgent皓骏从一个具体的题目为例，设计“三角形内接矩形面积最值问题”积件来说明如何运用皓骏积件来剖解教学难点，培养学生用数学的眼光观察世界、用数学的思维思考世界和用数学的语言表达世界的能力。本文首先介绍了Hawgent皓骏制作“三角形内接矩形面积最值问题”积件的设计原理和步骤，然后给出了其在教学中的应用的两点思考。

1 应用Hawgent皓骏设计“面积最值问题”的原理及制作步骤

1.1 积件的设计原理

设计原理是基于Hawgent皓骏软件的功能，并遵循矩形面积的算法和二次函数图象的性质。绘制出三角形内接矩形，并用轨迹刻画内接矩形面积与其一边长度之间的关系，测量出内接矩形面积，以便数形结合。提供面积最值问题动态积件的一般做法，可如法炮制到三角形内接正方形、扇形的内接矩形面积的最值问题等。

1.2 积件的制作步骤

1.2.1 绘制三角形

首先，选择“画图工具”，在空白页任意点击生成一个点A，选中点A依次点击“变换”|“数字平移”，输入x=5，y=0后点击“确定”得到点B；接着，依次选中点A、点B，点击“绘制”|“约束点”|“对象上的点”，得到线段AB上的一个自由点C。选中点C，“变换”|“数字平移”，输入x=5，y=0后点击“确定”得到点D。然后，依次选中点A、点B、点D，选择“绘制”|“线段”，得到△DAB。切换到“画笔工具”，连接点D与点C，得到线段DC也是DAB的高。最后，依次选中点D、点C、点B，点击“构造”|“标记”。如图1。

图1

1.2.2 绘制内接矩形

首先，依次选中点A、点D，点击“绘制”|“约束点”|“对象上的点”，得到线段AD上的一个自由点E。接着，依次选中点E、线段AB，点击“绘制”|“垂足”得到垂线EF。然后，依次选中点E、线段AB，点击“绘制”|“平行线”得到一条平行直线线；依次选中这条平行直线、线段BD，点击“绘制”|“交点”，得到交点G，选中该平行线，同时按住“Ctrl+H”，将其隐藏。最后，依次选中点G、点E、点F，点击“绘制”|“四边形”|“平行四边形”，得到矩形EFGH。如图1。

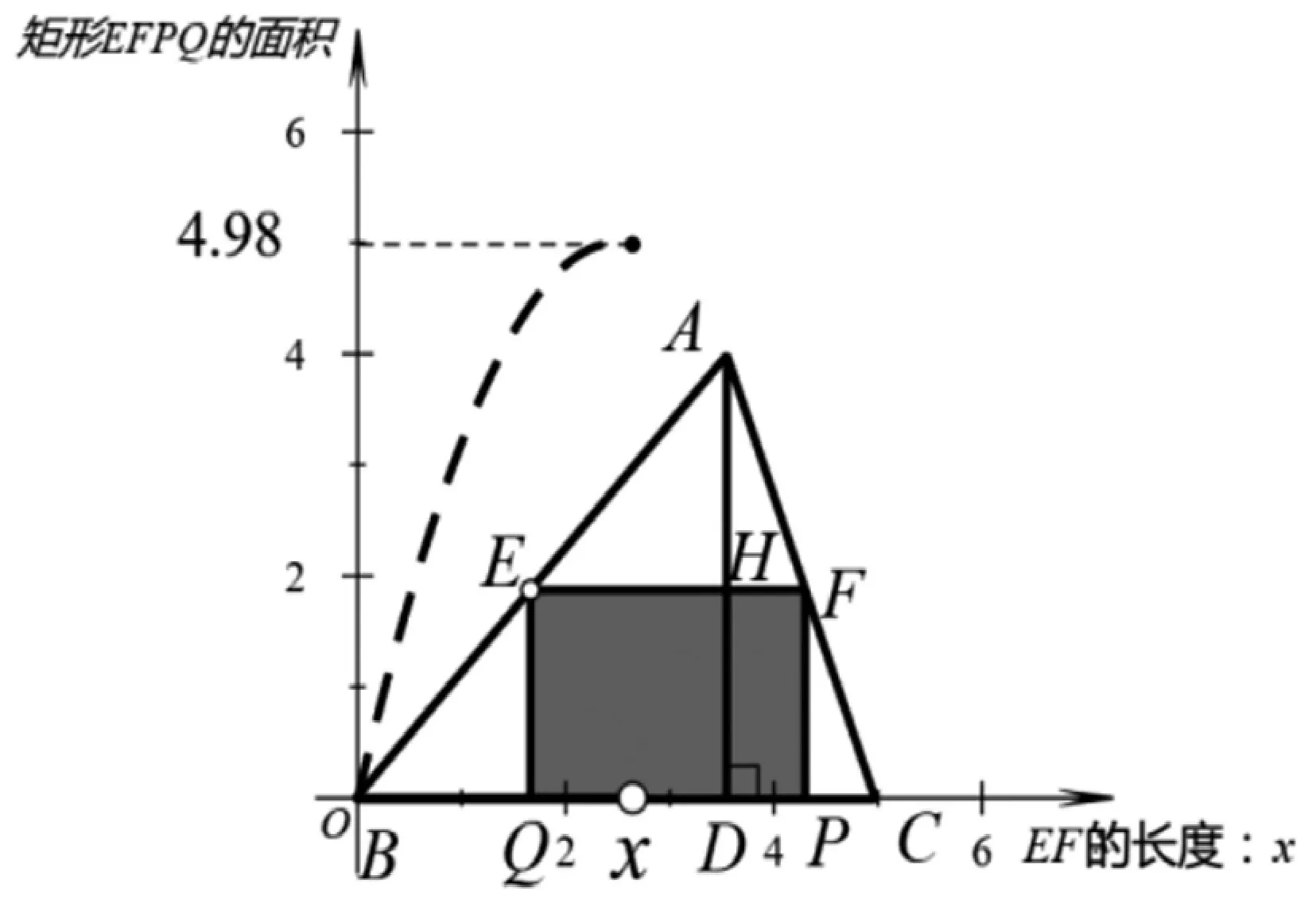
图2

1.2.3 绘制二次函数

首先，选中线段EG，点击“测量”|“长度”，得到数据线段EG的长度，其变量名为u000；接着，点击“绘”制|“一般曲线”|“函数：y=f(x)”，输入函数f(x)=4x-4/5x^2(根据题目信息，计算出内接矩形面积与x的函数关系式)，a=0，b=u000，样本点为1000个（目的是让二次函数图形更平滑）。最后，点击“绘制”|“坐标点”，输入点（u000，4u000-4/5u000^2）得到点 I；点击“绘制”|“坐标点”，输入点（u000，0）得到点J，连接线段AJ。如图2。

1.2.4 美化界面

（1）美化坐标点：选中所有坐标点，点击“设计”|“点的大小”，点的大小设为1，再点击“字号”，字号为24。按照题目要求将坐标点的标注修改至于题目一致。

（2）美化线段：选中图中所有线段，点击“设计”，双击“增加”以此加粗线段。

（3）美化矩形，依次选中矩形的四个顶点，点击“绘制”|“多边形”，选中这个多边形，点击“设计”|“填充”更改颜色为黑色。

（4）美化二次函数图象：选中二次函数图象和线段AJ，点击“设计”|“线型”|“虚线”，将其设为虚线。

（5）优化坐标系：坐标系，右击鼠标，在弹出的对话框中点击“常规”，将y轴的坐标改为“矩形EFPQ的面积”。如图2。

2 积件的主要教学应用

与传统教具展示或“粉笔+黑板”的板书相比，本积件能数形结合地直观展示三角形内接矩形面积的变化过程，灵活应用积件辅助于教学，有可能会提效本节课的教学。

2.1 直观暴露思维过程，辅助培养几何直观

首先根据波利亚解题表，厘清好题目的已知条件、未知条件以及解决问题需要到的由已知条件推理出的隐含条件后，提问学生猜想点E在什么位置时，该三角形内接矩形面积最大？通过猜想的思维体操，锻炼学生的几何直观想象能力。此时辅助以本积件，通过拖动点E，使其在线段AB上运动，引导学生观察矩形面积的大小变化。接着，通过所绘制的矩形面积与EF长度x的函数图形，同步追踪矩形面积与x之间的大小变化关系。数与形的碰撞结合，动与静的相互交织，以此来验证猜想，进一步推动拟定计划的进程。经历探索、猜想、观察、验证的基本活动，体悟数形结合的数学思想，培养几何直观的数学核心素养与主动探索的勇敢精神。

2.2 纵横变式拓展深化，助力锻炼发散思维

通过“你见过类似的问题吗？”这个问题，借助题干具体的数值与题目，引导学生进一步推理运算，把矩形的最值问题转化为二次函数求最值问题，渗透转化、数形结合思想。此处积件作用有二：其一是，拖动三角形的一个顶点，任意改变三角形的形状与大小，从特殊到一般，纵向变式探究任意三角形的内接矩形面积最值问题是否有同样的结论？其二是拖动矩形的一边使其一组邻边相等从而变为正方形，横向变式探究三角形内接正方形面积最值问题。最后变式升华，扇形、圆形内接矩形的面积最值问题又有怎样的规律呢？至此，一连串紧凑的题目纵横向全方位的数学变式基本活动，体现了动态信息技术在较传统教学的优越性，深化学生对相似三角形的性质、二次函数最值等基本知识的理解，授之以鱼；体悟数形结合、转化与化归的数学思想，授之以渔；给力学生几何直观和数学建模的数学核心素养的发展，授之以愉。