不同安装模态对嵌入式时栅测量误差的影响

孙世政，周清松，韩 宇，何泽银

(重庆交通大学 机电与车辆工程学院，重庆 400074)

1 引 言

随着制造加工及位移检测等领域的快速发展，对末端位置检测提出了更高的要求[1-5]。由于受到传感机理、空间结构和安装条件的局限，难以有效地实现对位置的直接检测，因此迫切需要研制一种能实现末端位置直接测量的新型传感器。

嵌入式时栅传感器是一种将被测旋转机械与传感器融为一体的新型角度传感器，其基于“时空转换原理”将时间差转换为空间角度差进行间接测量，具有体积小、重量轻、抗强干扰等优点，主要用于高速、重载、中空等特殊工况下的角度测量[6-7]。随着测量环境的复杂化，实现传感器在复杂条件下测量精度的表征，提升测量精度成为了传感器研究的重要内容。时栅传感器的测量误差主要来源于激励信号误差、电路误差和安装误差[8]。目前对时栅传感器由激励信号误差与电路误差引起的测量误差规律进行了大量研究，杨洪涛等人[9]分析了零点残余电压与激励信号误差对测量精度的影响规律。刘小康等人[10-11]分析了时栅传感器激励信号幅值不等造成的测量误差形式。范兵等人[12]分析了节距偏差对时栅传感器的误差影响规律，建立了节距偏差的误差模型。安装误差作为传感器测量误差中不可忽略的部分，研究人员对安装偏差引起的测量误差也进行了研究，鲁进等人[13]通过仿真分析的方式对变耦式时栅不同测头姿态下的误差形式进行了研究。Peng K等人[14]对电容式时栅纳米传感器不同安装模态下测量精度的影响规律进行了研究，建立了不同安装模态下的误差模型。针对嵌入式时栅传感器安装误差，杨洪涛等人[15]通过仿真分析的方式，对寄生式时栅传感器由测头与转子不同间隙、测头的俯仰角和偏摆角大小变化对测量精度的影响规律进行了研究。孙世政等人[16]对嵌入式时栅传感器转子安装偏心对测量精度的影响规律进行了研究。以上研究虽分析了不同安装模态对时栅传感器测量精度的影响规律，但针对在安装气隙变化、径向安装偏差和轴向安装偏差下对嵌入式时栅传感器测量误差的影响研究仍不完整，未形成较系统的安装误差模型。

本文基于嵌入式时栅传感器机械结构与传感机理，建立了安装气隙变化、径向安装偏差和轴向安装偏差等不同安装模态的误差模型，分析了不同安装模态对测量精度的影响规律。搭建了实验平台对传感器不同安装模态下的测量精度进行了比对测量，通过对不同安装模态下测量精度影响规律分析，明确了安装偏差对测量精度的影响规律，实现了不同安装模态下测量精度的表征。本文研究为时栅传感器安装与误差修正提供了理论依据。

2 传感器工作原理

嵌入式时栅传感器机械结构如图1所示，由传感测量头和转子两部分组成，转子为被测旋转机械部件。传感测量头由测头齿和绕组构成，绕组分为激励绕组层与感应绕组层，其中激励绕组层由A，B两组激励绕组构成。

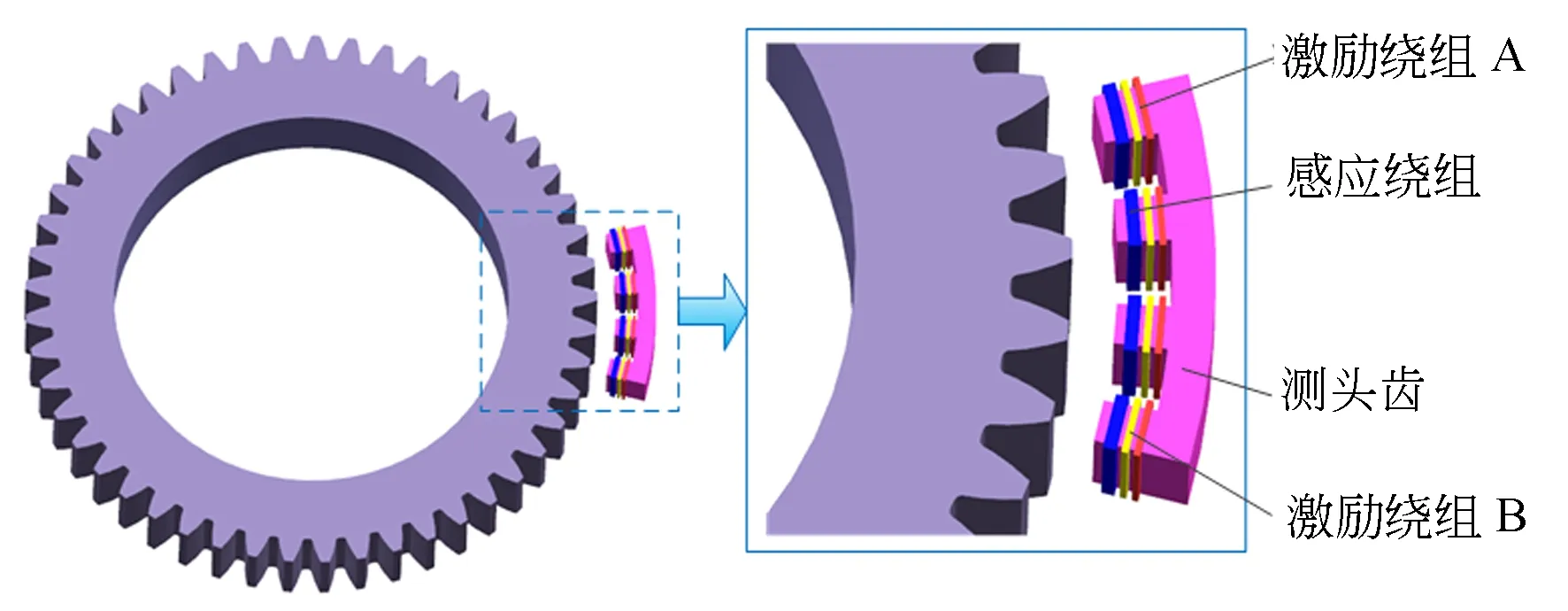
图1 传感器机械结构示意图Fig.1 Schematic diagram of sensor mechanical structure

嵌入式时栅传感器在激励绕组A上通入正弦激励，激励绕组B上通入余弦激励以实现激励信号在时间上的正交，通过控制激励绕组A，B的绕法实现空间正交。当被测旋转机械部件与测量头发生相对位置变化时，感应信号随测量头与被测旋转机械部件气隙的变化而成周期性变化，感应绕组分别输出两组既有时间信息又有空间信息的驻波A和B，驻波信号为：

(1)

式中:Um为激励信号幅值，θ为角度值。

驻波A和B通过叠加合成的方式合成行波信号，行波信号为：

U=Umsin(ωt+θ).

(2)

传感器测量原理如图2所示。将行波信号U与一组激励信号UA送入信号处理模块，利用高频时钟脉冲对激励信号与行波信号进行插补处理，在时间测量模块中获取反映被测旋转机械角位移值的时间差ΔT并将其送入数据处理模块，在数据处理模块中实现对测量角度的求解，最后将所得角度θ值送入显示模块进行角度显示。

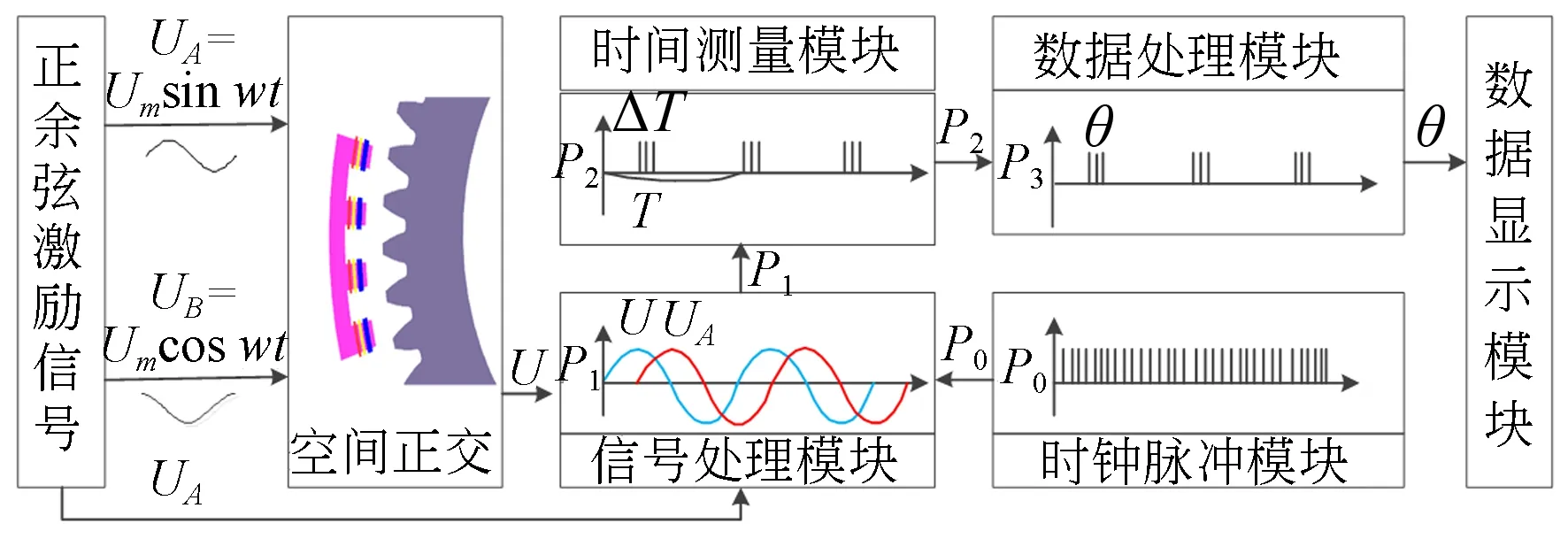
图2 测量原理图Fig.2 Measurement schematic diagram

3 传感器不同安装模态误差产生原理分析

嵌入式时栅传感器在测量过程中，应保证安装的精确度与重复度，但由于加工误差与人为因素的影响在安装过程中将导致测量误差的产生。根据对嵌入式时栅传感器机械结构与传感机理的分析，传感器主要存在三种形式的安装偏差模态，安装气隙变化、径向安装偏差和轴向安装偏差。上述三种安装偏差均引起传感器感应信号发生改变，从而导致测量误差。

3.1 安装气隙变化误差产生原理分析

嵌入式时栅传感器受测量头安装及加工误差等因素影响，在测量过程中测量头与被测旋转机械之间气隙厚度发生变化，从而引起励磁回路的改变，导致测量误差产生。安装气隙变化时传感器结构示意图如图3所示。

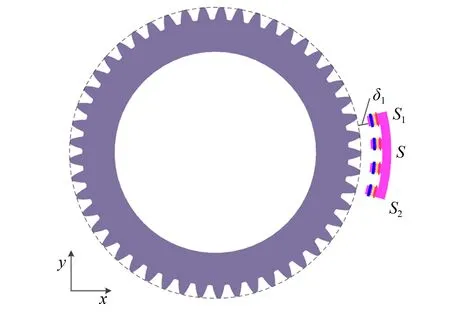
图3 安装气隙变化示意图Fig.3 Schematic diagram of installation gaps deviation

图中，δ1为气隙厚度，S为测量头长度，s1与s2分别为测量头起始与终止位置。

安装气隙变化时驻波UAg和UBg表达式为：

(3)

式中Ug1与Ug2为两列驻波信号的幅值。

安装气隙变化时行波信号UG为：

(4)

由于测量头尺寸远小于被测旋转机械且气隙厚度为毫米级，因此将测量头内圈与被测旋转机械外圈视为两条平行线。

A相驻波上单位节距的感应电势幅值为：

(5)

式中：c为感应电势系数；τ为节距；其中τ=ws，w为测量头宽度。

感应绕组中感应电势幅值为：

(6)

同理，可知B相驻波上感应信号幅值为：

(7)

由于测量头与被测旋转机械之间为均匀气隙，气隙变化为同步变化，因此可知Ug1=Ug2。式(4)可表示为：

UG=Ug1sin(ωt+θ).

(8)

由上述分析可知，安装气隙变化影响传感器测量精度。

3.2 径向安装误差产生原理分析

嵌入式时栅传感器在安装过程中，由于测量头与被测旋转机械在径向上安装轴线不平行，导致径向偏移角存在。径向偏差将导致测量头与被测旋转机械之间气隙厚度与相对节距发生变化，产生测量误差。传感器径向安装偏差示意图如图4所示。

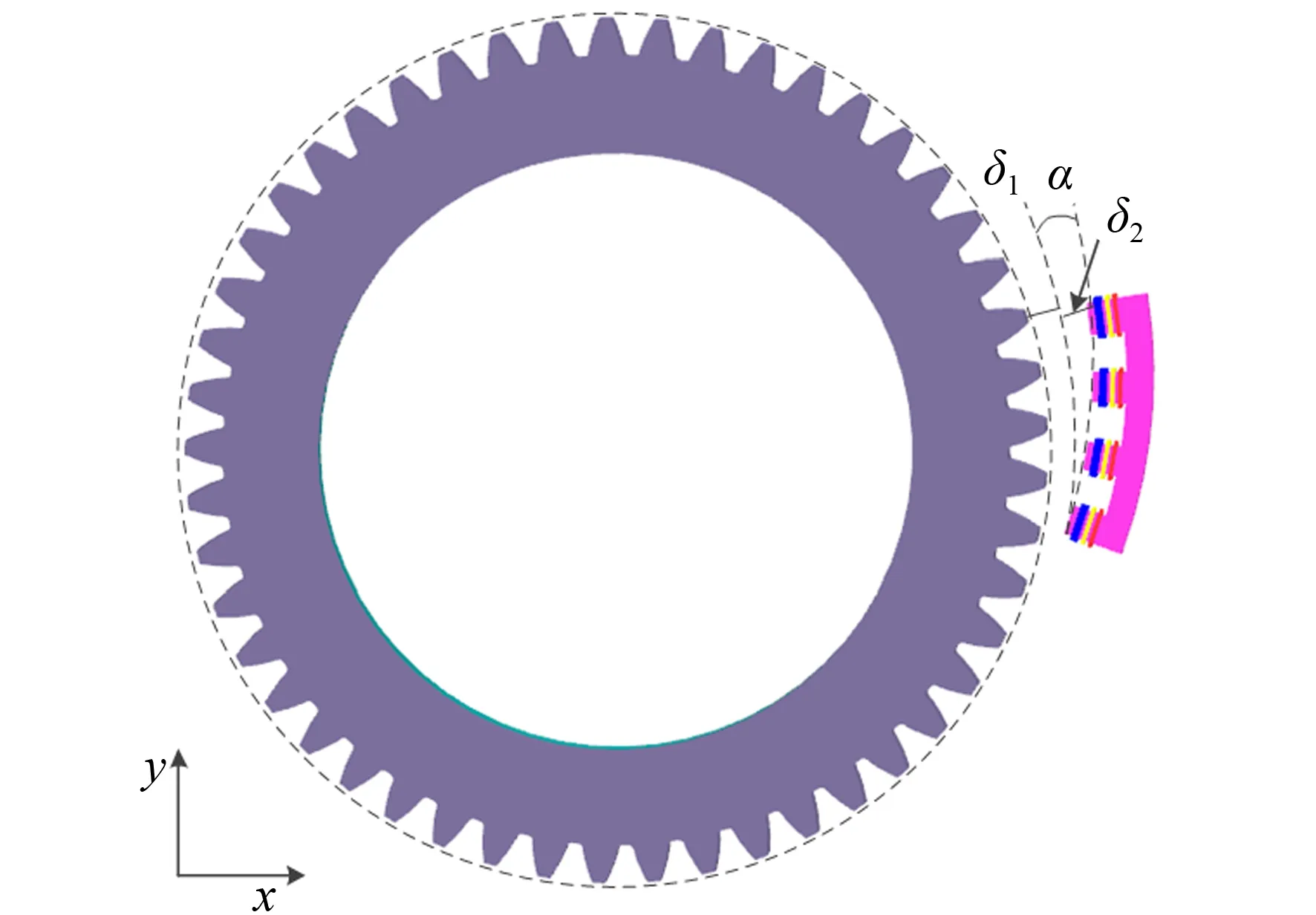
图4 径向安装偏差示意图Fig.4 Schematic diagram of radial installation deviation

图中，α为径向安装偏移角，δ2为偏移导致的气隙变化厚度。

径向安装偏差时驻波UAr与UBr表达式分别为：

(9)

式中:Ur1与Ur2分别为两列驻波信号幅值；φ为空间正交相上的偏心误差项。

径向安装偏差时，A，B相与齿轮之间气隙变化厚度相同，此时感应电势幅值Ur1=Ur2为：

(10)

当气隙厚度与初始厚度相同时，此时感应电势与初始电势幅值Um相同，引入平均节矩τp与平均气隙则Um可表示为：

(11)

将式(10)代入式(11)有：

(12)

此时行波信号UR为：

UR=Ursin(ωt+θr)，

(13)

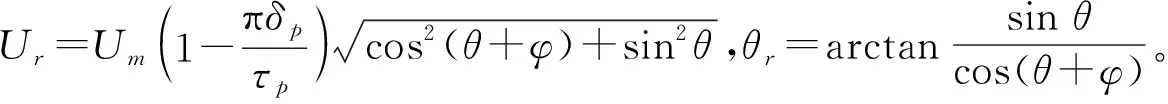
由式(13)可见，传感器径向安装偏差将引起测量信号幅值与相位的改变。

3.3 轴向安装误差产生原理分析

嵌入式时栅传感器在安装过程中，由于测量头与被测旋转机械在轴向上安装轴线不平行，导致轴向偏移角存在。轴向安装偏差将导致测量头与被测旋转机械的相对节距发生变化，引起励磁回路发生改变，产生测量误差。传感器轴向安装偏差示意图如图5所示。

图5 轴向安装偏差示意图Fig.5 Schematic diagram of axially installation deviation

图中，β为轴向安装偏移角。

轴向安装偏差时驻波UAa与UBa表达式分别为：

(14)

式中:Ua1与Ua2分别为两驻波信号幅值；ε为空间正交相上的偏心误差项。

当测量头在轴向存在偏移角时，测量头在被测旋转机械上的节距发生变化，此时变化后节距为τa=τsinβ，且A,B的节距变化相同。

轴向安装偏差时感应电势幅值Ua1=Ua2为：

(15)

此时行波信号UA为：

UA=Uasin(ωt+θa)，

(16)

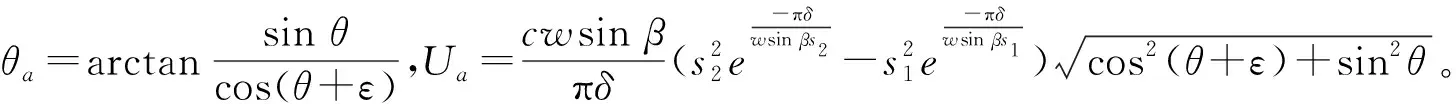
由式(16)可知，传感器轴向安装偏差将导致测量信号幅值与相位的变化。

4 建模仿真与误差分析

4.1 有限元建模与参数设置

为研究不同安装模态对嵌入式时栅感应行波的影响，实现对传感器测量误差规律的分析，基于嵌入式时栅结构与传感原理，利用ANSYS MAXWELL软件对传感器的不同安装模态进行了电磁仿真。仿真结构示意图如图1所示，电磁仿真设置如下：仿真求解器设置为瞬态电磁器；嵌入式时栅对极数设置为400，每个对极对应的空间角度为0.9°(360°/400 = 0.9°)；正弦激励绕组匝数为40匝、余弦激励绕组匝数为40匝、感应绕组匝数为120匝；激励为电压激励，正余弦激励表达式分别为UA=8sin(2π×400t)V，UB=8cos(2π×400t)V；绕组材料设置为铜、转子材料设置为45号钢、定子材料设置为坡莫合金；线圈绕组网格最大边长设置为0.8 mm，转子网格最大边长设置为2 mm，定子网格最大边长设置为0.8 mm，真空域网格最大边长为10 mm；运动步长设置为0.022 5°(0.9°/40)。

4.2 安装气隙变化仿真

传感器在实际安装中测量头与被测旋转机械之间的气隙变化范围为0.15 mm～0.5 mm，根据传感器实际安装精度，在仿真模型中气隙间距分别设置为0.2,0.3,0.4,0.5 mm，图6为感应行波在不同气隙间距下的仿真结果。

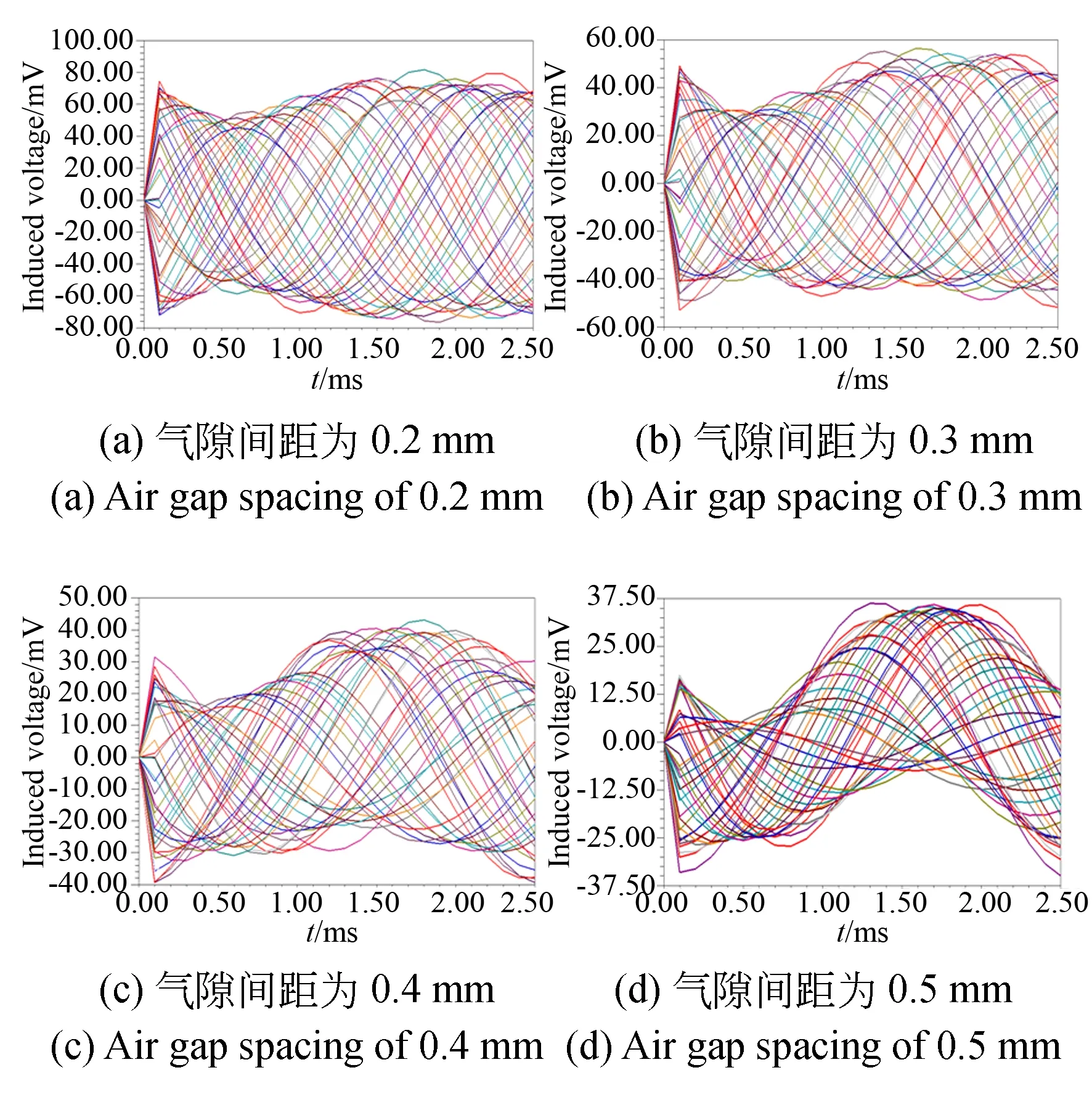
图6 不同气隙间距的行波仿真结果Fig.6 Line wave simulation results for different air gap spacing

为明确不同气隙间距下传感器的测量误差，对图6中4组行波信号分别进行FFT处理，计算每条曲线的初相位，并令初始位置曲线的初相位为零，以仿真结果与理论初相位相减，得到各空间位置的相位差。其中令仿真初相位为αm，理论初相位为α，则各空间位置相位差与测量误差可表示为：

αr=αm-α，

(17)

(18)

由式(17)与式(18)可得传感器在不同气隙间距下的测量误差曲线，如图7所示。表1为不同气隙间距下的误差分析结果。

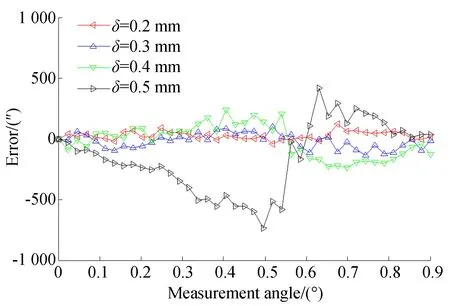
图7 气隙间距变化测量误差曲线Fig.7 Error curve for measurement of air gap variation

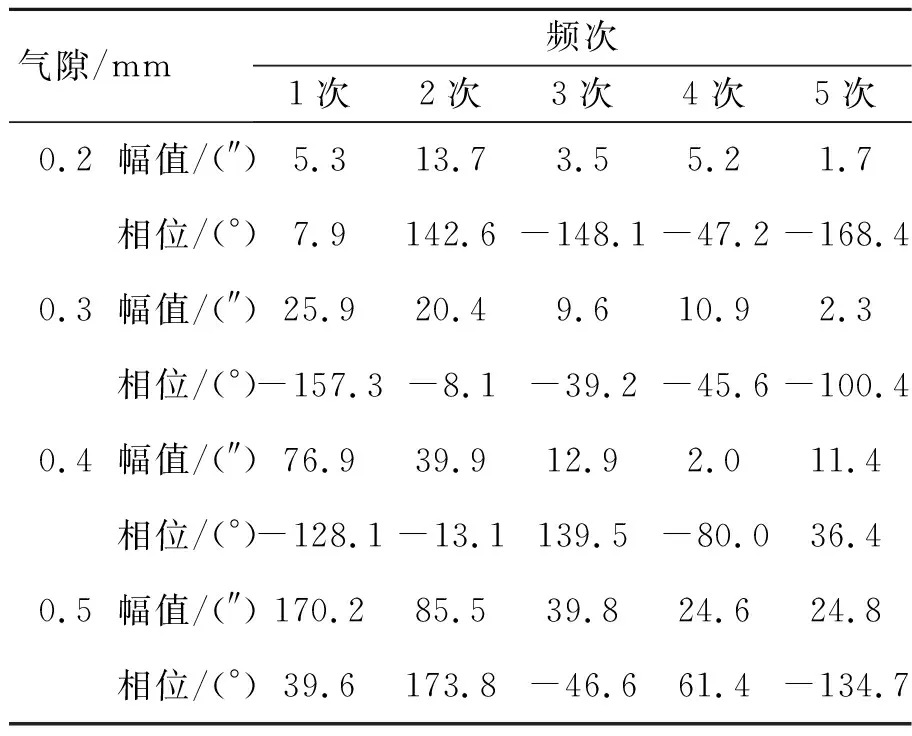
表1 不同安装气隙误差分析Tab.1 Air gap error analysis for different installations

由图7与表1分析可知，当气隙间距为0.2 mm，0.3 mm，0.4 mm和0.5 mm时误差峰峰值分别为159.5″，238.1″，471.1″和1 150.4″。当气隙间距为0.2 mm时，二次误差最大，其值为13.7″。当气隙间距为0.3 mm时，一次和二次误差较大，其值分别为25.9″和20.4″。当气隙间距为0.4 mm时，一次与二次误差分别为76.9″和39.9″。当气隙间距为0.5 mm时，相对于气隙间距为0.2 mm，0.3 mm和0.4 mm时误差变化明显，一次与二次误差幅值分别为170.2″和85.5″，其他频次误差较小。

由分析可知，测量误差随气隙间距的增加而变大，当气隙间距为0.5 mm时，误差明显增加。测量误差主要为一次和二次误差，同时还伴随有其他频次的误差，其他频次的误差可能是由于传感器自身性质或在仿真过程中网格质量不合格而导致。因此为保证传感器气隙间距对测量误差的影响减至最小，应保证测量头与被测旋转机械之间安装尺寸的情况下使得气隙间距尽量小，从而获得较大的输出信号同时避免误差的增加影响测量结果。

4.3 径向安装偏差仿真

传感器在实际安装中测量头与被测旋转机械之间的气隙变化范围为0.15 mm～0.5 mm，径向安装偏移角变化范围为0°～2°。根据传感器实际安装精度，在仿真模型中气隙间距设置为0.2 mm，径向安装偏移角分别为1°和2°，图8为感应行波在不同径向安装偏移角的行波仿真结果。

将所得行波信号按前述方法计算初相位，并依据式(17)和式(18)计算测量误差。测量误差如图9所示，表2为不同径向安装偏移下的误差分析结果。

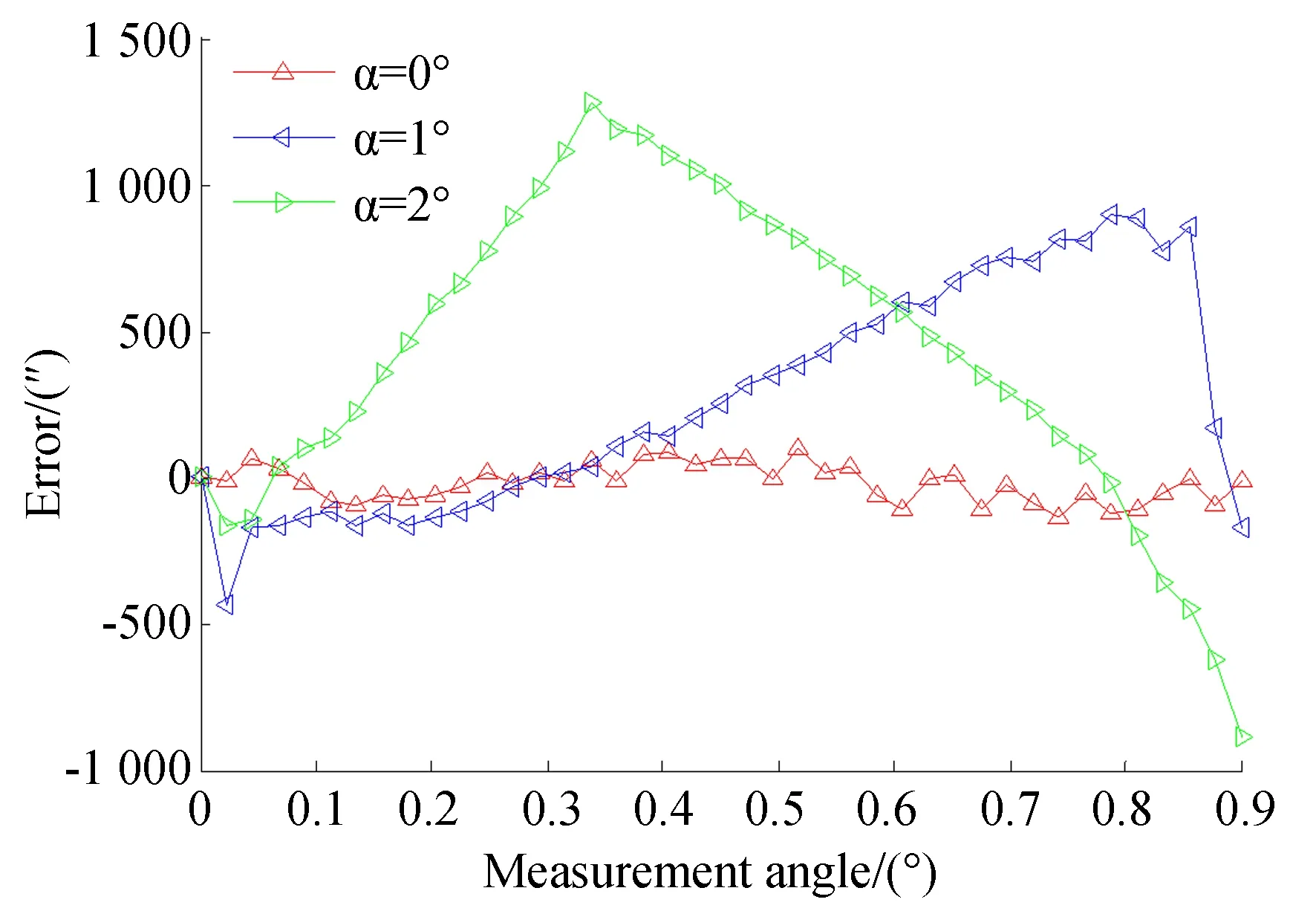
图9 不同径向偏移下的误差曲线Fig.9 Error curves for different radial offsets

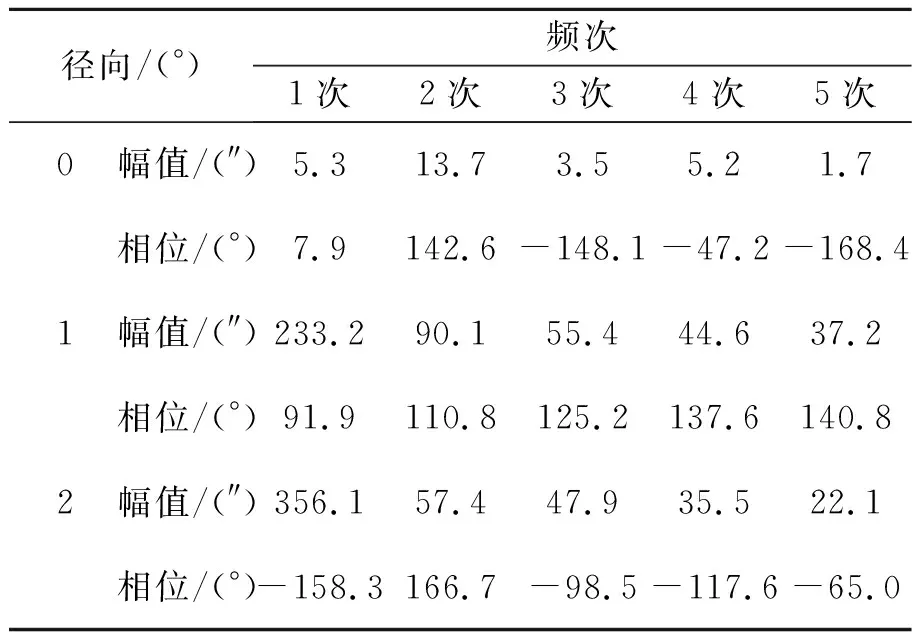
表2 不同径向偏移误差分析

由图9与表2分析可知，当径向偏移角分别为1°和2°时，其对应的误差峰峰值分别为1 335.9″和2 166.3″。当气隙间距为0.2 mm，径向偏移角为1°时，误差呈现增减增的变化趋势，在0.33°时误差最大，幅值为1 278″，误差中一次与二次误差为主要误差，其幅值分别为233.2″和90.1″。当气隙间距为0.2 mm，径向偏移角为2°时，误差呈现先增后减的变化趋势，在0.78°时误差达到最大值902.2″，误差中一次与二次误差为主要误差，其幅值分别为356.1″，和57.1″。

由分析可知，嵌入式时栅在安装过程中发生径向偏移时，测量误差随径向偏移角的增加而明显增大，其主要产生一次和二次误差，且一次与二次误差随径向偏移角的增加而变大，同时还伴随有其他频次的误差，其他频次的误差可能是由于传感器自身性质或仿真过程中网格质量不合格而引起。因此为保证传感器安装过程中，安装对传感器测量精度的影响减至最小，应在安装过程中尽量避免径向安装偏差的产生。

4.4 轴向安装偏差仿真

传感器在实际安装中测量头与被测旋转机械之间的气隙变化范围为0.15 mm～0.5 mm，轴向安装偏移角变化范围为0°～2°。根据传感器实际安装精度，在仿真模型中气隙间距设置为0.2 mm，轴向安装偏移角分别为1°和2°，图10为感应行波在不同轴向安装偏移角的仿真结果。

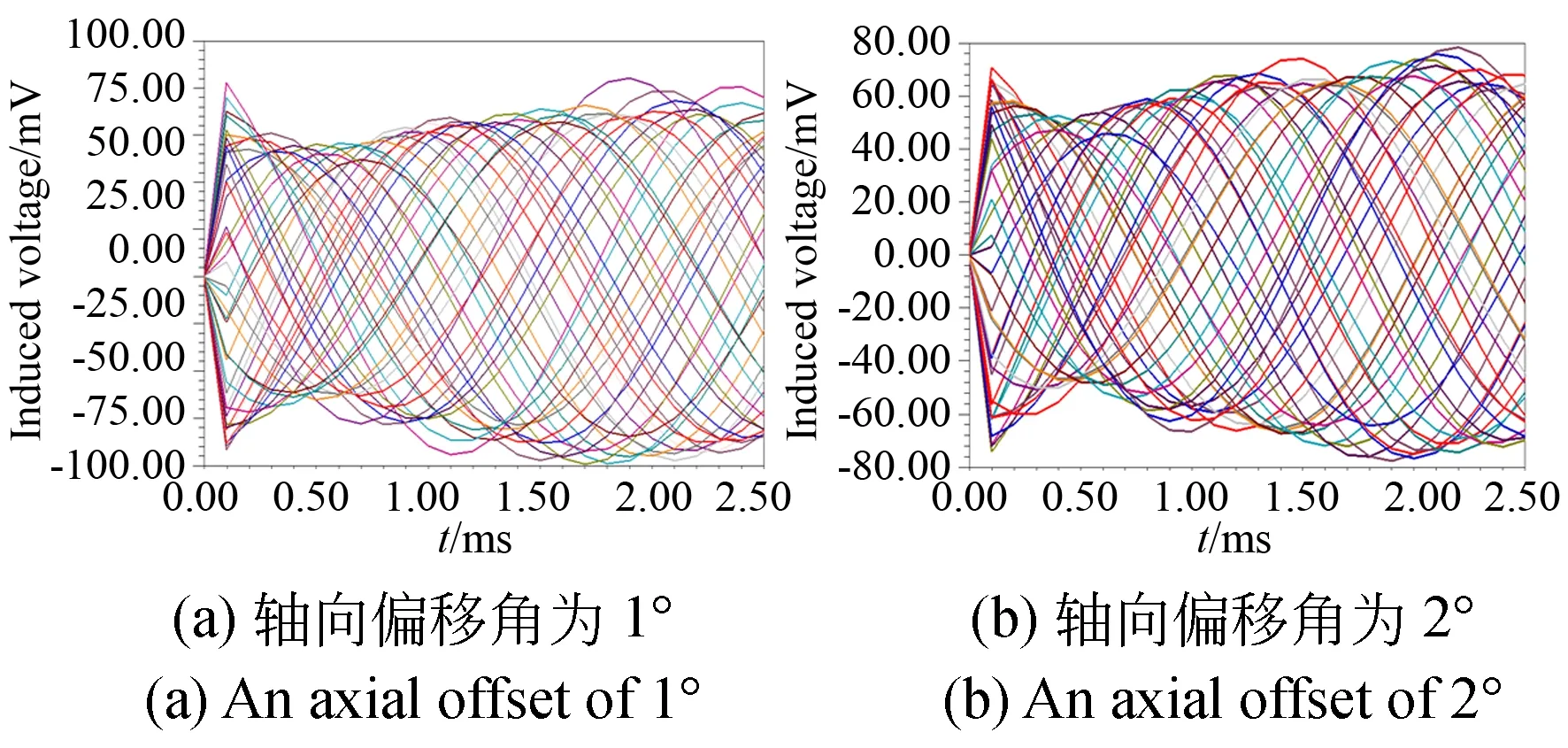
图10 不同轴向偏移的行波仿真结果Fig.10 Line wave simulation results for different axial shifts

将所得行波信号按前述方法计算初相位，并依据式(17)和式(18)计算仿真下的测量误差。测量误差如图11所示，表3为不同轴向安装偏移的误差分析结果。

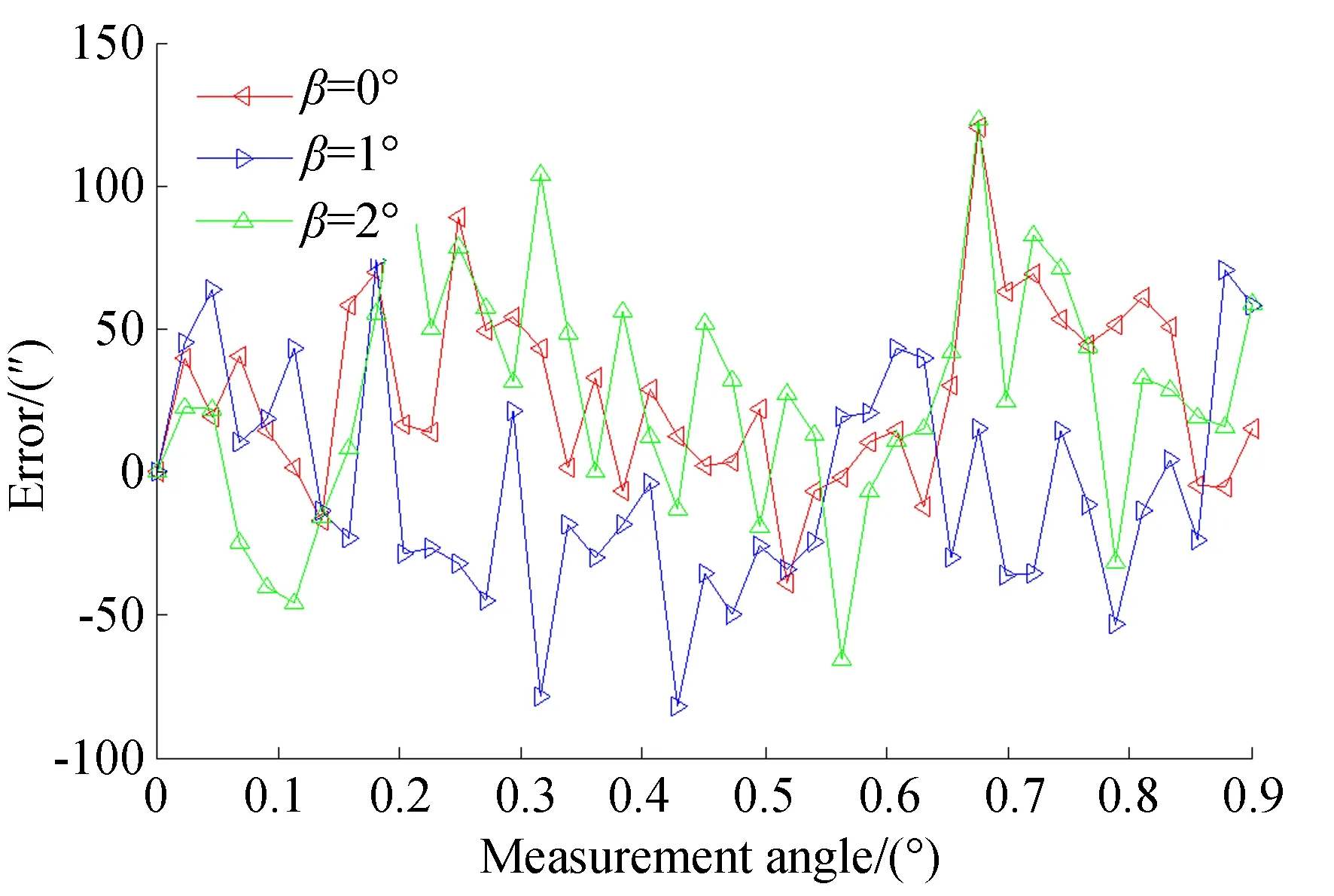
图11 不同轴向偏移下的误差曲线Fig.11 Error curve for different axially offsets

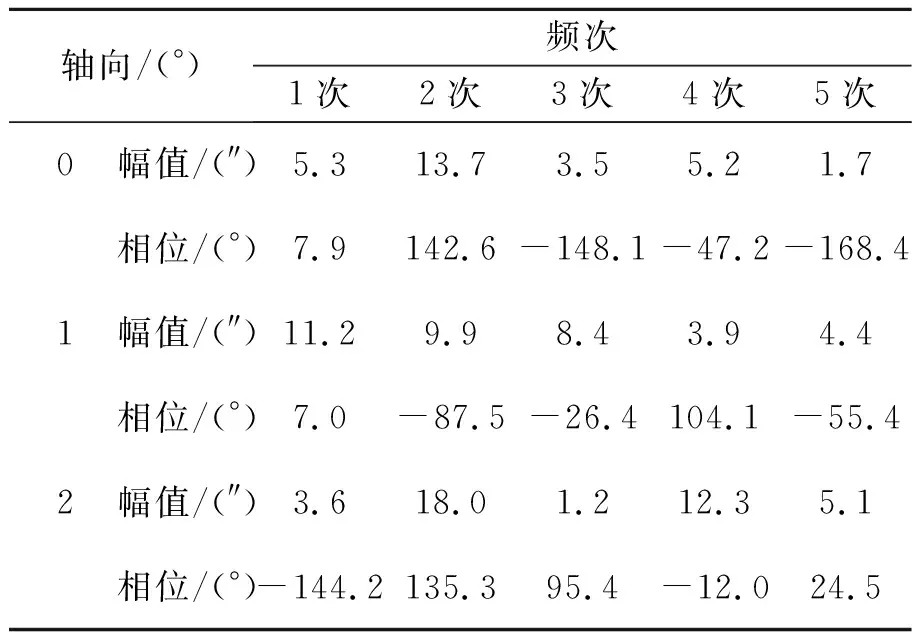
表3 轴向安装误差分析

由图11与表3分析可知，当轴向偏移角分别为1°和2°时，误差峰峰值分别为156.2″和188.6″。当气隙间距为0.2 mm，轴向偏移角为1°时，一次误差为主要误差，二次误差其次，幅值分别为11.2″和9.9″。当气隙间距为0.2 mm，轴向偏移角为2°时一次与二次误差分别为3.6″和18.0″。

由分析可知，传感器轴向安装对测量精度影响较小。嵌入式时栅在安装过程中发生轴向偏移时，其主要产生一次和二次误差，且一次误差随轴向偏移角度数先增加后减少，二次误差随偏移角增加而增加，整体误差随偏移角的增加而缓慢增加，但变化幅度不大。同时还伴随有其他频次的误差，其他频次的误差可能是由于传感器自身性质或在仿真过程中网格量不合格而导致。轴向偏移对传感器测量精度影响较小。

5 实验验证与误差分析

5.1 实验系统搭建

为验证理论推导与模拟仿真的正确性，搭建了嵌入式时栅传感器实验系统。实验系统如图12所示。

图12 实验系统图Fig.12 Experimental system

将嵌入式时栅传感器与光栅通过弹性联轴器安装在精密分度转台主轴上，由控制系统驱动齿轮做匀速运动，以实现嵌入式时栅传感器与光栅对齿轮的同步测量。其中以测量精度为0.8"的海德汉圆光栅作为基准仪器，以Delta-Tau旗下可编程多轴运动控制器(PMAC)为控制器，以Motorola旗下DSP5600系列芯片作为CPU。通过改变嵌入式时栅传感器的安装模态以实现不同安装模态的角度测量，将光栅测量值近似作为真实角度值，光栅与嵌入式时栅传感器测量结果之差即为测量误差。

5.2 安装气隙变化实验

进行嵌入式时栅传感器安装气隙变化实验时，首先将测量头与齿轮同心安装并以塞尺相隔，为避免加工误差所致的不规则齿轮与毛刺对测量头的直接接触，气隙间距最小设定为0.2 mm。然后改变塞尺厚度以获取不同的气隙间距，气隙间距分别设置为0.2，0.3，0.4和0.5 mm。不同气隙间距下传感器误差曲线如图13所示，表4为不同气隙下的误差分析结果。

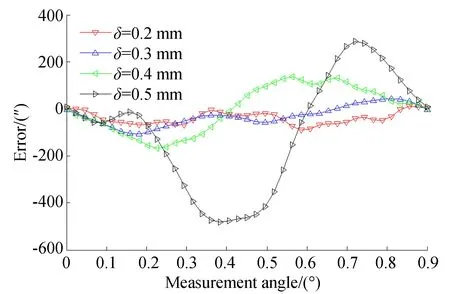
图13 不同安装气隙误差曲线Fig.13 Error curve of different installation gaps

根据图13与表4可知：气隙间距为0.2 mm,0.3 mm,0.4 mm和0.5 mm时误差峰峰值分别为100.8″，102.0″，150.1″和604.6″。气隙间距为0.2 mm时，误差较小并呈现增减增减的变化趋势，其中一次与二次误差为主要误差。当气隙间距为0.3 mm时，误差相对间距0.2 mm时稍有增加，在0.18°时误差到达最大值105.8″，误差中一次和二次误差较大，其幅值分别为23.4″和17.3″。当气隙间距为0. 4 mm，在0.22°时，误差达到最大值168.1″，误差中一次与二次误差越发明显，其幅值分别为67.4″和17.7″。当气隙间距为0.5 mm时，误差变化较明显，在0.38°时，误差到达最大值479.8″，其中一次与二次误差分别为155.9″和70.7″，其他频次误差相对较小。

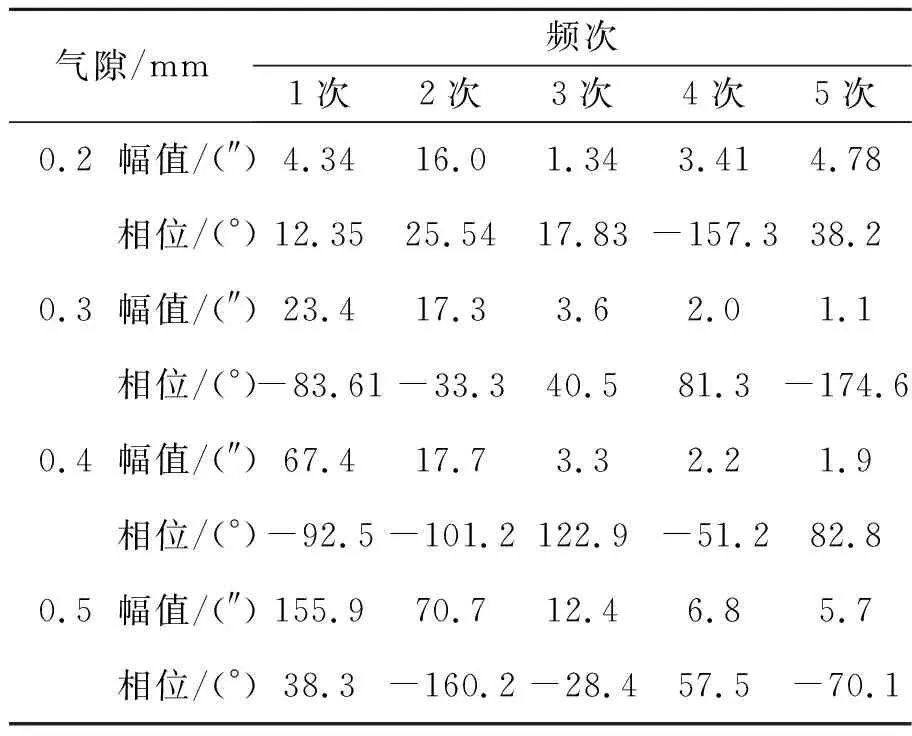
表4 不同安装气隙误差分析

由实验可知，当嵌入式时栅气隙间距变化时，测量误差随气隙间距的增加而变大，气隙变化主要引起一次和二次误差的增加。实验结果与理论推导和模拟仿真的结果基本吻合，因此在嵌入式时栅安装过程中，应保证测量头与被测旋转机械之间安装尺寸的情况下使得气隙间距尽量减小，从而避免误差的增加影响测量结果。

5.3 径向安装偏差实验

进行嵌入式时栅传感器径向安装偏差实验时，首先将测量头与齿轮之间以塞尺相隔，初始气隙间距设置为0.2 mm。然后保持测量头一端塞尺厚度不变，改变另一端塞尺厚度以获取不同的径向偏差角，本次实验径向偏差角分别为1°和2°。不同径向偏差角下误差曲线如图14所示，表5为各径向安装误差的分析结果。

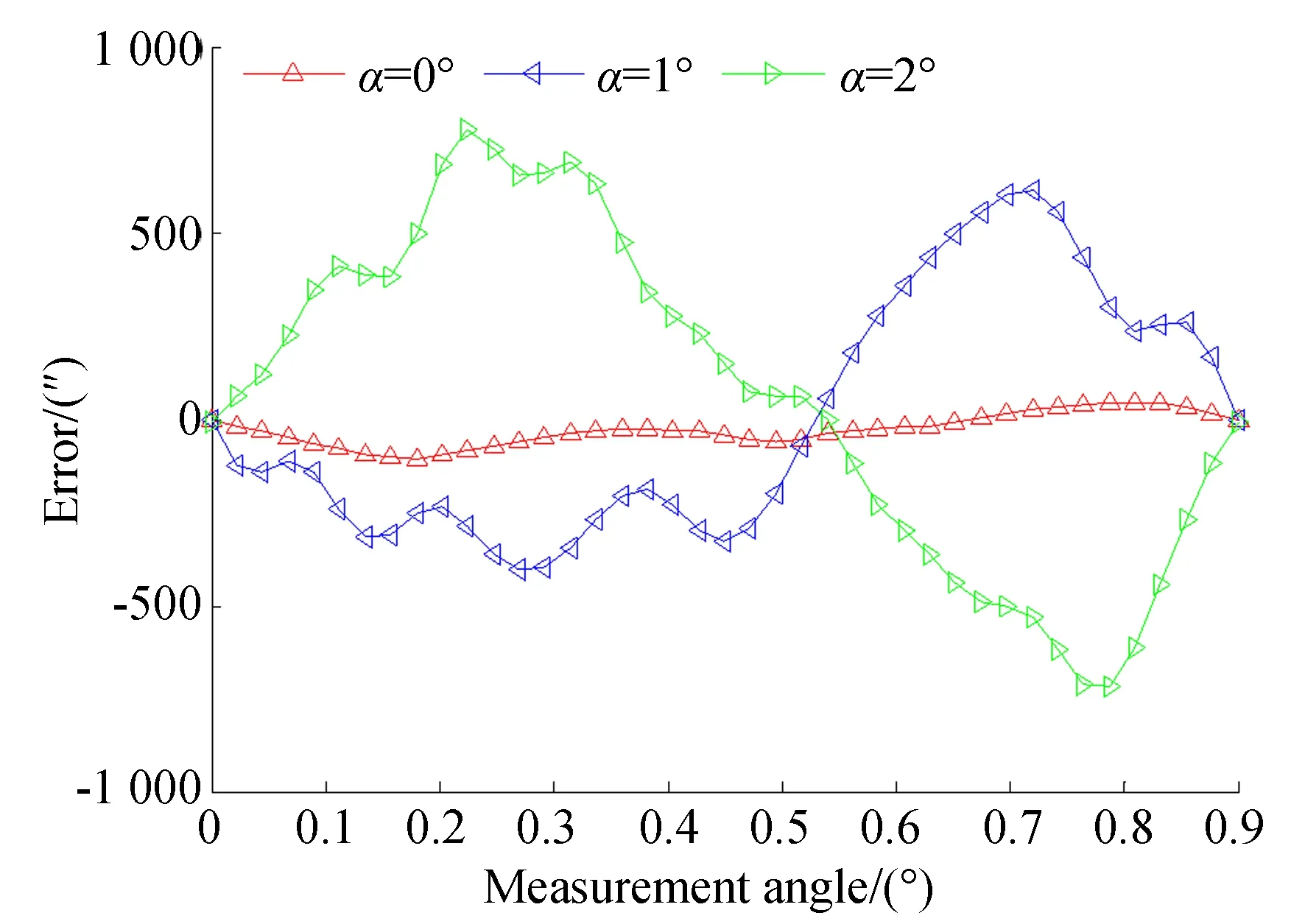
图14 径向安装误差曲线Fig.14 Error curve of radial installation

表5 径向安装误差分析

根据图14与表5可知：气隙厚度为0.2 mm，径向偏移角分别为1°和2°时测量误差峰峰值分别为1 016.4″和2 044.5″；径向偏移角为1°时，其相对于无径向偏移时，测量误差有较大的增加，在0.72°时误差达到最大值611.1″，其中一次和二次为主要误差，其幅值分别为213.4″和63.9″。当径向偏移角为2°时，由于产生的测量误差较大将会导致测量值失真，在0.78°时误差达到最大值878″，误差中一次和二次误差仍然为主要误差，其幅值分别为306.8″和38.1″。

由实验可知，当嵌入式时栅在安装过程中存在径向安装偏移角时，将会对测量结果产生较大的影响，且随径向偏移角的增加而增加，径向安装偏移角的变化主要通过引起一次和二次误差的变化而引起测量误差整体变化。实验结果与理论推导和模拟仿真的结果基本吻合，因此在嵌入式时栅安装过程中，应保证尽量避免径向偏移角的产生。

5.4 轴向安装偏差实验

进行传感器轴向安装偏差实验时，首先用塞尺将气隙间距固定为0.2 mm，然后保持气隙间距不变测量头一端不动另一端用量块踮起合适角度，改变量块厚度以获取不同的轴向偏差角，本次实验轴向偏移角度分别为1°和2°。不同轴向偏差角度下整周误差曲线如图15所示，表6为各误差曲线的分析结果。

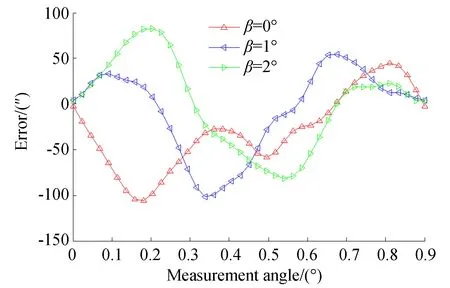
图15 轴向安装误差曲线Fig.15 Error curve of axially installation

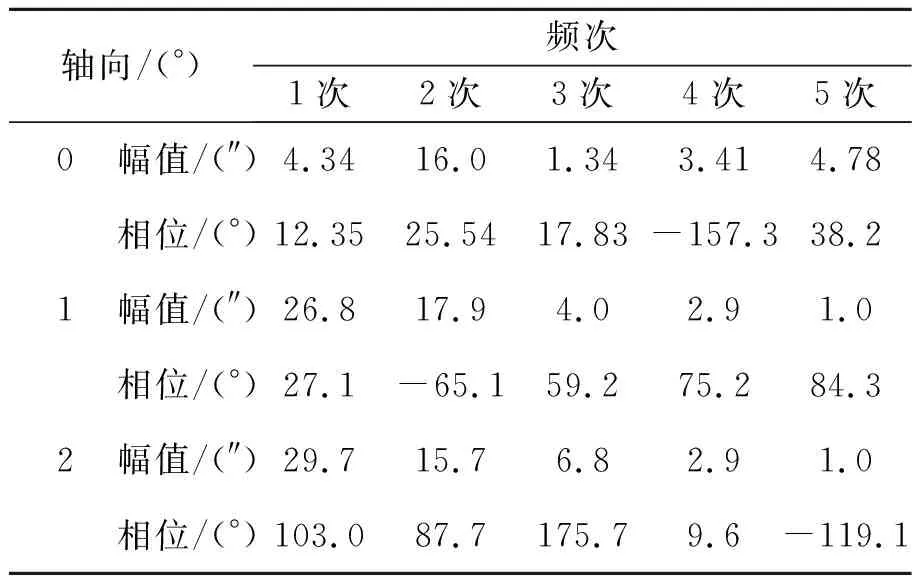
表6 轴向安装误差分析

根据图15与表6可知：气隙厚度为0.2 mm，轴向偏移角分别为1°和2°时测量误差峰峰值分别为155.6″和164.4″；当轴向偏移角为1°时，其相对于无轴向偏移，测量误差增加较少，在0.33°时误差最大，最大值为101.3″，一次与二次误差分别为26.8″和17.9″。当轴向偏移角为2°时，测量误差相对于无轴向偏转和轴向偏转为1°时无较大变化，在0.2°时误差值最大，最大为82″，误差中一次和二次误差为主要误差，其分别27.9″和15.7″。

由实验可知，当嵌入式时栅安装过程中存在轴向安装偏移角时，其对测量结果产生的影响较小，测量误差基本不随轴向偏移角的增加而增加。实验结果与理论推导与模拟仿真的结果基本吻合，轴向偏移对嵌入式时栅影响较小。

6 结 论

嵌入式时栅传感器安装误差由多种安装偏差引起，其中主要为安装气隙变化、径向安装偏差和轴向安装偏差。为实现对嵌入式时栅传感器不同安装模态下测量精度的表征，本文基于嵌入式时栅传感器机械结构与传感原理，建立了不同安装模态对传感器测量精度的影响模型。然后针对传感器不同安装模态下的误差特性进行了模拟仿真与实验验证。仿真与实验结果均表明：不同安装模态均会影响传感器测量精度，其中径向安装对传感器测量误差影响最大，气隙间距变化对传感器测量误差影响其次，轴向安装对传感器测量误差影响最小；主要通过改变一次误差和二次误差来改变整体误差；因此嵌入式时栅在安装过程中应保证气隙间距尽量小，本文所用的400对极传感器气隙间距取0.2 mm为宜；传感器径向安装偏差对测量精度影响最大，在安装过程中应尽量避免径向安装偏差的产生；本文的研究对指导传感器安装和提升传感器测量精度具有重要的理论与现实意义。