主轴动态回转误差测量技术

金 岸，缪寅宵，刘冬冬，林 杰，金 鹏*，王 雷

(1.哈尔滨工业大学 超精密光电仪器工程研究所，黑龙江 哈尔滨 150080；2. 超精密仪器技术及智能化工业和信息化部重点实验室(哈尔滨工业大学)，黑龙江 哈尔滨150080；3. 北京航天计量测试技术研究所，北京 100076;4. 92493部队计量测试研究所，辽宁 葫芦岛 125000)

1 引 言

在以集成电路生产为代表的半导体加工领域中，新型集成电路器件正向着高集成化、高密度化和高性能化的方向发展。电子产品在集成度、运行速度和可靠性不断提高的同时也向着轻薄短小的方向发展。与此同时，新型半导体封装技术不断涌现，这些先进的封装技术对晶圆的品质提出了更高的要求。在半导体制程中，需要先将晶圆减薄并切割成一个个独立的单元，然后将这些单元制成不同的半导体封装结构，即芯片。晶圆减薄与晶圆切割是半导体封装工艺中的关键制程，因此整个工艺的产能主要依赖于减薄机和划片机的品质。

减薄机与划片机中的核心部件是高速主轴。近年来，在高端数控机床领域出现的高速电主轴，是将机床主轴与主轴电机融为一体的新技术。高速数控机床主传动系统取消了带传动和齿轮传动，机床主轴由内装式电动机直接驱动，从而把机床主传动链的长度缩短为零，实现了机床的“零传动”。这种主轴电动机与机床主轴“合二为一”的传动结构形式，使主轴部件从机床的传动系统和整体结构中相对独立出来，因此可做成主轴单元。高速高精度电主轴具有转速快、轴系精度高、使用寿命长、运转平稳等优点，因而主要应用于半导体加工装备和超精密机床等高端加工制造领域。

随着半导体加工技术和超净加工技术的发展，该领域对高速超精密主轴的技术需求也日益增加。主轴转速从几千转每分钟上升到几万转每分钟，主轴的轴系精度也在不断提高。例如径向回转误差从几百微米降低到几十微米甚至几微米。英国Loadpoint公司生产的减薄机中主轴最高转速达120 000 r/min；日本DISCO公司生产的划片机中主轴最高转速高达60 000 r/min，轴系的径向回转误差优于2 μm。

在用于半导体晶圆加工的划片机中，主轴的径向回转误差会导致划片深度的变化，可能导致切割深度不足，晶圆无法顺利分离，或者切割深度过大，导致晶圆损坏，过大的径向回转误差甚至会损毁划片机刀具。主轴的轴向回转误差会引起划片走向的偏移，导致晶圆切割不规则。在减薄机中，主轴的轴向回转误差会影响刀片在减薄方向上的线性进给，从而影响晶圆的表面粗糙度甚至破坏晶圆。通过测试与分析主轴的回转特性，可以预测机床加工工件所能达到的形状误差及表面粗糙度，从而对机床加工误差进行补偿控制。此外，对主轴回转特性的测试与分析还可以用于主轴运转状态的判断，诊断主轴故障。因此，测量高速主轴动态回转特性相关的参数具有重要的现实意义。

2 主轴回转误差测量方法

在机床生产的早期阶段，还没有一种广为接受的机床性能测试方法，要实现可靠的加工精度是十分困难的。20世纪20年代末，德国工程师Schlei.singer博士提出了第一批标准化测试(DIN)用来检测制造机床的零件[1]。Schlei.singer具有开拓性的想法，获得了机床行业的广泛认可。虽然同样的测试方法至今仍在沿用，但它们却无法测量出机床的实际性能。直到20世纪50年代，第一批检测机床性能方法的出现，这一问题才得以解决。在家乡捷克斯洛伐克工作时，Schlei.singer与Tlusty博士共同开发了一种动态测量机床主轴误差运动的方法，该方法简称为Tlusty法[2]。后来，主轴旋转法替代了Schlei.singer的基础质量检测方法，使得人们意识到当把主轴用于机械加工时，主轴会怎样运作。20世纪60年代至70年代，Tlusty博士陆续开发出了很多项测试技术，成功地将机床性能与机床所生产的零件关联起来[3-5]。到了20世纪80年代，“柔性制造”成为研究热点，过去以零件性能取胜的做法不再实用。在车间开始使用新机床制造零件之前，机床用户便开始询问机床整体性能是否有保障。劳伦斯利弗莫尔国家实验室的Bryan博士开发了校准机床精度的工具和技术，他发明了伸缩球杆仪，这项发明后来成为验证机床性能的一种重要工具[6]。Bryan提倡采用更精确的方法来验证机床性能，并一直强调测量主轴误差运动的重要性，而不是主轴光亮表面的跳动[7]。因此，该领域的研究方向逐渐转移到主轴本身误差运动的测量上，所采用的技术手段大致分为两类。一类是以位移传感器与标准器为核心器件，将标准器轴心与主轴回转轴心重合安置，将位移传感器安置在标准器的径向上，以固定回转角度为步进控制主轴转动。以特定角度为相位零点，用位移传感器测量主轴回转一周过程中标准器与位移传感器之间的位移变化量，并以此为基础解析出主轴径向回转误差。另外一类是以激光器、标准球和光电探测器为核心器件，通过光路设计与精密装调，将激光照射到标准球上，反射光被光电探测器采集，通过评价主轴回转过程中光电探测器上的光强变化来评价主轴径向回转误差。

2.1 基于位移传感的主轴回转误差测量

三点法是一种广泛应用的误差分离技术，由日本学者青木保雄和大圆成夫在1966年首次提出[8]。该方法成为多点法误差分离技术中一个经典的误差分离方法，国内外许多学者对该方法进行了大量的研究，使三点法误差分离技术的应用得到了很大的提高和推广。1972年，Donaldson首次提出反向法误差分离技术，对主轴回转误差和被测工件的形状误差进行分离[9]。反向法后来也发展成为一种广泛应用的误差分离技术。

20世纪90年代，Noguchi等人提出了矢量指示法，用垂直于轴线的平面上的矢量来表示和计算主轴的径向回转误差运动[10]。实验中，用两个相互垂直的位移传感器对固定在主轴端面的标准球进行测量，并开发一种算法来获取主轴轴线位移的瞬时矢量。以矢量指示法表征主轴运动误差可以获得比传统方法“李萨如”图更精确的结果。1996年，Gao等人首次提出混合法测量圆度误差，即用两个线位移传感器和一个角位移传感器同时进行测量，测量原理如图1所示[11]。与三点法相比，混合法能够将圆度误差和主轴的回转误差进行完全分离，也能很好地测出表面形貌里的高频成分。在此之后，Gao等人基于混合法提出新的误差分离方法——正交混合法，该方法只用一个线位移传感器和一个角位移传感器，相互成90°布置[12]。正交混合法是对混合法的改进，其传感器布置更为简单，测量效果在实验中也得到了印证。

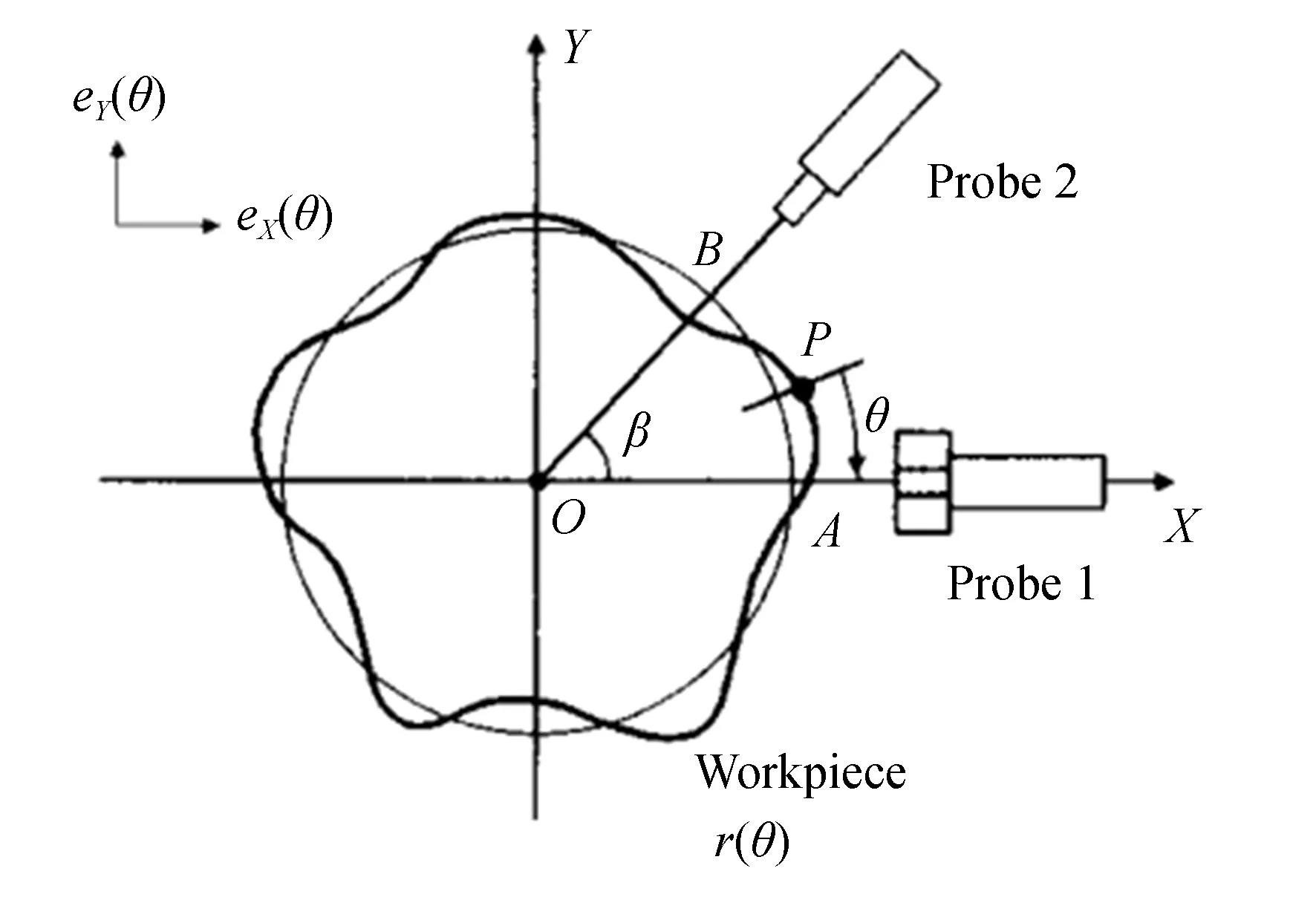
图1 混合法的测量原理[11]Fig.1 Principle for mixed method[11]

2005年，Grejda等人对Donaldson提出的反向法进行了改进，将被测主轴安装在转盘上，并在主轴和工件之间使用特殊的卡盘(称为反转卡盘)，如图2所示[13]。被测主轴的定子相对于工件和量规旋转，而不是像传统方法那样相对于主轴的定子旋转量规和工件。该方法通过设计新的转台形式减少了位移传感器的移动和调整，可靠地消除由热漂移和空气轴承供气压力波动引起的低频成分。此方法测得的结果重复性误差优于1 nm。

2007年，Gao等人基于双探头主轴误差测量设计了一套金刚石车床主轴误差测量和运动补偿系统，通过补偿加工获得了很好的工件表面平整度[14]。2010年，Marsh等人对反向法和多点法误差分离技术进行了实际测量及比较，文中重点研究这两种误差分离算法对纳米级误差分离的可行性，实验验证了它们对主轴回转误差和工件表面形状误差亚纳米级分离的可靠性和可重复性[15]。2012年，Gao等人提出了一种主轴误差运动测量系统来评估一个大型精密轧辊车床的主轴，利用反转法分离形状误差和主轴运动误差，通过对不同截面数据的测量，计算主轴的径向运动误差和倾角运动误差[16]。2012年前后，美国雄狮精仪公司研发了一套五自由度主轴回转误差分析仪，采用5个电容位移传感器对双标准球杆进行测量。每个标准球布置两个互为 90°的传感器，轴端的标准球轴向位置布置一个传感器，完成主轴径向运动误差、倾角运动误差和轴向运动误差的测量。

图3 雄狮精仪公司的5探头主轴测量仪Fig.3 Five-probe SEA of Lion Precision

2014年，Cappa等人利用一种新的误差分析方法比较和评估各种已知的多探针测量技术[17]。他们提出了一种新式的多探头测量技术，在测试过程中并不需要对标准器及传感器的准确定位，并且对不同传感器灵敏度具有鲁棒性。

国内于20世纪80年代前后开始对主轴回转参数计量技术的研究。1978年，哈尔滨工业大学蔡鹤皋对主轴回转运动精度进行研究，系统地描述了主轴回转运动精度的各个概念，并前瞻性地指出应当对主轴的动态参数进行测量[18]。蔡鹤皋指出，主轴回转运动精度测量可以分为静态测量法和动态测量法。当对以正常速度运转的主轴状态进行测量时，才反映出主轴回转运动的真实情况。1982年，重庆大学钟先信指出传统主轴回转运动精度测量中的两个问题[19]：一是静态测量与动态工作状态不一致，往往测量精度高而工作精度低；二是标准球的形状误差及安装偏心都反映在测量值中，应当进行分离。1983年，上海交通大学洪迈生介绍了用三点法临床分离机床主轴径向误差运动和工件形状误差的数学原理和分析方法[20]，提出将傅里叶变换应用到误差分离中。1990年，清华大学叶京生等人研究了多步法误差分离技术的原理性误差和测量精度[21]，从理论和实验证实了多步法能够完整地分离主轴回转误差和被测件的圆度误差，有效地提高了圆度仪的测量精度。1995年，哈尔滨工业大学王晓慧等人提出了实时测量机床主轴回转误差的方法，并建立了一套在线测量及补偿系统[22]，实验表明，加入在线测量及补偿后，加工工件的圆度误差平均改善了40%，圆柱度误差平均改善了23%。1997年，洪迈生提出时域二点法来分离圆度误差和回转误差[23]。对布置在测试件周向的接近180°的两个传感器的测量数据进行时域上的分离，并进行实验对比该方法和频域三点法测量结果的差别，证明了该方法的有效性。1999年，中国船舶工业总公司6354所阚光萍介绍了双向转位法测量主轴的径向回转误差[24]，该方法实质为反向法的应用。阚光萍从测量仪器读数误差的角度对安装偏心的大小与分离精度关系进行了研究。2000年，第三军医大学陈海斌等人提出了正弦回归法分离标准球的安装偏心，利用反向法进行误差分离，剔除标准球的形状误差，实现了主轴回转精度评定[25]。2000年，洪迈生等人提出了时域三点法进行误差分离，相对于频域三点法，此方法避免了正逆两次傅里叶变换，分离速度更快。由于此方法是在频域三点法的基础上建立的，在实验前同样要用频域三点法中的权函数来检验三个传感器安装位置对谐波的抑制问题。其时域分离是一个迭代的过程，迭代初值的确定是时域分析的一个掣肘问题，其原理性误差的根源是迭代初值的不确定性[26]。2001年，哈尔滨工业大学谭久彬等人对回转基准中存在的问题进行了分析，并分析了多步法误差分离技术的原理误差，提出鉴相法误差分离技术，扩展了无谐波抑制范围，并简化了测量过程和系统[27]。2002年，国防科技大学李圣怡等人提出用两点法误差分离技术分离超精密车床主轴回转误差和圆度误差的方法，建立相应的数学模型并进行仿真[28]。该测试系统只是从主轴敏感方向测量，应用受到一定局限，主要用来评价主轴的工作精度和预测车床在理想加工条件下所能达到的最小形状误差。李圣怡等人基于上述计算仿真，还对超精密车床主轴回转误差运动进行了测试，实验表明回转误差运动中二次分量占主要成分[29]。与此同时，洪迈生等人采用机床本身加工的工件作为被测试件，利用三点法频域误差分离技术对主轴的回转误差和被测试件的形状误差进行分离，采用自适应阈值的小波包算法除掉加工时存在的噪声，从谐波抑制特性和总体频域特性两个方面分析测量系统的频域特征，以此实现主轴径向运动误差的在线误差测量[30]。2003年，洪迈生等人继续使用频域三点法进行主轴回转误差运动的测量[31]，提出了先使用频域法确定工件表面形状误差的误差初值, 然后用时域三点法测量数控机床主轴运动误差的新方法，该方法有效解决了限制时域三点法应用的初值问题。2004年，长春工业大学梁淑卿等人采用双向测试法对主轴的回转精度进行动态测试[32]。该方法应用曲线拟合法对测量信号中与转速同频的偏心运动和主轴误差运动中的一次误差运动进行了有效的识别分离, 消除了偏心运动, 实现了主轴误差的准确评定。

2012年，Samuel在前述工作的基础上，提出了一种基于模型的曲线拟合方法，在时域中准确地解释和分析主轴误差测量数据，并与常用的基于离散傅里叶变换的频域滤波方法进行了比较，该方法为主轴误差数据的基频估计提供了更高的分辨率[33]。2013年，Lan等人采用两个非接触式电容传感器来测量旋转主轴的径向跳动[34]。2015年，Wu等人提出了一种改进的两点测量方法，用于高速镗杆的径向微位移测量，该系统由两个正交位移传感器和一个角度编码器组成[35]。2017年，Zhao等人提出了求解多变量方程法(SSME)，简化了传统三探针方法的数学处理过程，提出了一种新的三探针测量方法，该方法对常规三探针法难以测量的角度具有良好的鲁棒性[36]。

上述方法大多基于大圆成夫所提出的“三点法”。尽管学者们尝试采用不同的方法对此进行改进，但仍然不可避免地存在两个方面的缺陷。首先，基于多探头(位移传感器)的主轴运动误差测量系统需要配合标准球或其他标准器完成，因此不可避免地引入标准器自身轮廓的误差以及安装误差；第二，为了准确地评价主轴回转运动误差，需要位移传感器在主轴回转一周的时间里采集足够多的信息。但是当主轴以工作状态运行时，受采样频率限制，位移传感器并不能够完成足够的数据采用。假设被测主轴转速超过60 000 r/min，主轴轴心点的晃动频率为1 kHz，传感器的采样频率应高于72 kHz，才能满足测量的基本要求，而目前具有高采样频率的位移传感器成本极高，难以制造。

2.2 基于光学手段的主轴回转误差测量

2004年，Liu等人使用自制的激光二极管装置替代了传统方法中的标准球，配合位置敏感探测器组成了一种新式的光学测量系统来对主轴回转误差进行测量，测量装置如图4所示[37]。

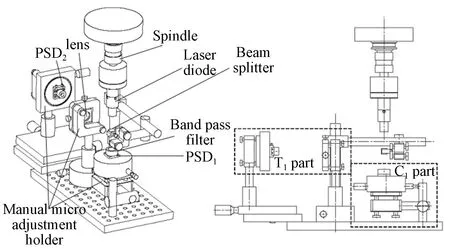
图4 Liu等人提出的测量装置[37]Fig.4 Schematic plot and coordinate definition proposed by Liu et al.[37]

2007年，Fujimaki等人开发了一种基于激光二极管和四象限光电探测器的光学测量系统，用于测量微型机床中主轴的径向跳动[38]。该方法中，激光二极管出射的光束通过分束器会聚到标准球上，通过评估标准球的反射光在QPD上的位移偏移量完成对主轴径向回转误差的测量，实验装置如图5所示。

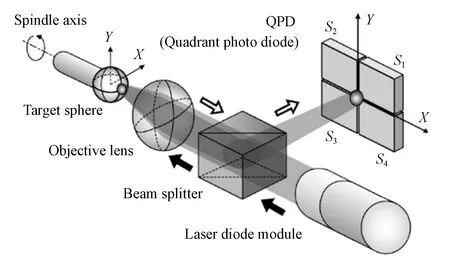
图5 Fujimaki等人提出的光学测量系统装置图[38]Fig.5 Optical layout for radial error measurements proposed by Fujimaki et al.[38]

基于类似的测量原理，Castro在2008年提出将激光干涉仪用于测量车床主轴旋转中的径向误差和轴向误差[39]。类似于雄狮精仪公司的测量手段，Murakami等人于2010年提出了一种用于测量高速微型主轴的五自由度误差运动的光学测量系统，该系统包括棒透镜、球透镜、4个分开的激光束和多个分开的光电二极管[40]，测量装置如图6所示。

图6 高速微型主轴五自由度误差运动光学测量系统[40]Fig.6 Optical measurement system of five-DOF error for high-speed micro spindle[40]

2012年，Ozdoganlar等人提出一种基于激光多普勒测振仪(Laser Doppler Vibrometer,LDV)对微加工设备中超高速主轴的径向回转误差进行测量的技术[41]。该方法将精密标准圆柱固定在主轴的回转端面上，控制主轴以其工作转速运行，使用两个LDV来测量标准圆柱轴向上两个不同位置处的径向运动，测量装置如图7所示。然后，对测得的径向运动进行处理，以获得主轴的径向误差运动。

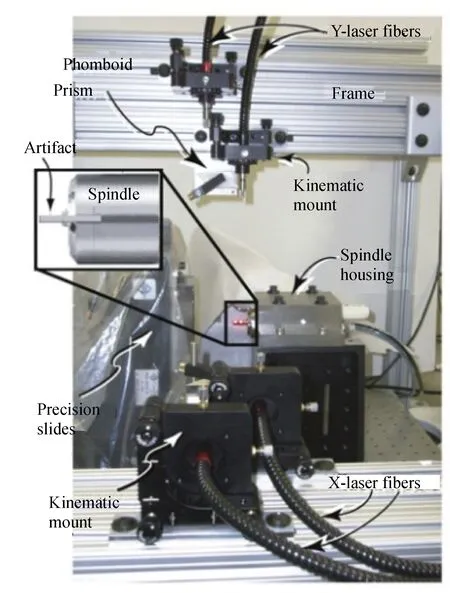
图7 基于LDV的主轴径向回转误差测量设备[41]Fig.7 Measurement setup for radial motion measurements based on LDV[41]

2013年，Ozdoganlar等人对上述方法进行了改进，将原有的精密标准圆柱改进为轴向端面安置有精密标准球的球杆型标准器件，新标准器件如图8所示[42]。此举将原有的两点测量改进为单点测量。同年，他们基于这种方法对超高速微加工主轴的误差运动进行了分析[43]。课题组分析了由于温度波动带来的影响，由于主轴转速改变带来的影响，以及轴承接触缺陷和工件安装误差带来的影响。并得出如下结论：(1)主轴长时间运行时，温度波动呈现周期性，显著影响主轴的运动误差；(2)主轴的转速和被测标准器悬垂的长度显著影响主轴的运动误差。

图8 Ozdoganlar等人提出的改进型标准器件[42]Fig.8 Model for diameter sphere-on-stem precision artifact fabricated to conduct axial and radial motion measurements[42]

2016年，Ozdoganlar等人对基于LDV的测量方法进一步完善，提出了一种多方向误差分离技术，以获得微型超高速主轴的径向误差运动[44]。与前述的方法不同，该技术既不依赖于高精度夹具，也不需要从工件的特定方向进行测量。而是使用LDV从工件任意方向测量主轴误差运动，测量步骤如图9所示。每个工件相对于主轴的方向设置角度是通过使用另一个LDV对在工件和主轴上所做的标记进行反射率测量而高精度确定的。

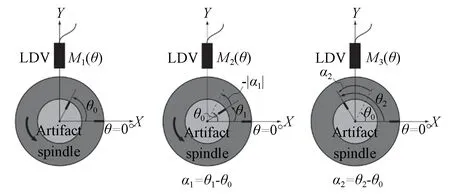
图9 采用三重定向时多定向技术中涉及的步骤[44]Fig.9 Steps involved in multi-orientation technique when using three re-orientations[44]

2013年，Garinei等人优化了一个基于光电传感器的测量系统设置，来测量高速电主轴转子的振动误差[45]。该方法指出可以通过建模获得转子的完整动态特征，并精确测量轴振动以跟踪转子的振动模式。2017年，Ashok使用机器视觉直接实现了高速主轴成像测量[46]。他们的方法有效地避免了复杂的测量系统，不需要具有高采样频率的电容传感器，该方法仅对最大转速为25 r/min的被测主轴有效。

图10 基于机器视觉实现机床主轴回转误差测量[46]Fig.10 Experimental arrangement for spindle radial error measurement using vision system in a lathe[46]

2019年，娄志峰课题组提出了一种在线非接触式测量主轴径向回转误差的方法。该方法主要由圆光栅、读数头、环形平面镜以及激光自准直仪组成。该方法与传统方法的测量精度相当,并且无需采用标准球，有效避免了标准球表面粗糙度、圆度等对测量结果的影响[47]。

与基于位移传感器的测量方式不同，上述方法大多是基于激光二极管和光电探测器实现的。这种方式很好地解决了传统方式应用于高速主轴动态参数测量时采样频率不足的问题，却不能解决测量过程中引入标准器自身精度及安装误差的问题。

3 主轴回转误差的数据处理和应用

3.1 混叠误差分离

不论是基于位移传感的测量方式，还是基于光学手段的测量方式，标准器都是不可或缺的。标准器的使用必定会引入标准器自身轮廓的面形误差及安装误差。因此，在测量过程中需要对混叠的误差进行分离。

1997年，Tu等人对传统的三探针测量法进行了精确几何建模，并在此基础上进行误差分析[48]，指出了三探针测量法基本方程中所做的近似处理。同时为了减少误差，标准轴的精度应该比主轴运动轴线的精度高十倍，传感器探针的安装误差应该小于主轴运动误差和标准轴尺寸的五十分之一。1999年，何钦象等人基于复数频域分析建立主轴回转运动数学模型，得出了主轴回转误差运动轨迹方程，定义了回转精度，定量分析了影响主轴回转精度的主要因素。何钦象指出主轴回转运动可用复函数来描述，进而分解为许多作圆周运动的频率分量，主轴的回转中心是主轴上回转的+1阶分量为零的点，主轴的误差运动不含+1阶分量[49]。2000年，洪迈生等人在回顾和评述误差分离技术的基础上，用多维误差分离技术理论将此前的多种误差分离技术进行了统一，给出了基于两个映射矩阵的一维和多维误差分离技术的统一方程。据此论述了误差分离的通则，以及误差分离技术的反滤波实质。并且，实现了圆度三点法、圆度转位法、直线乱序式四点法、直线精密三点法、圆度混合三点法、圆柱体五点法、平面混合四点法和摆线齿轮三点法的统一矩阵方程表示[50]。洪迈生等人于2004年对比了一般多步法的频域解和时域解，讨论了多步法的本质，指出标准器圆度误差和主轴回转误差的多步法误差分离系统本质上是一个可用传递函数描述的并联系统，其分离所得的标准器圆度误差中都存在着谐波损失，且该损失被残留在分离所得的主轴回转误差中。从而提出了一种并联多步法误差分离方法，该方法具有步数和谐波损失较少的优点[51]。2006年，Marsh等人对Donaldson反向法、多步法及多点法3种常用的误差分离技术在精密主轴和旋转对称工件的纳米级测量方面的应用进行了对比[52]。通过实验比较了Donaldson反转法、多步法和多探针法，证实了3种方法都能完成纳米级误差分离，其数值误差都优于1 nm。

2003年，陈清等人对以圆柱体作为标准器的主轴径向回转误差测试系统的误差进行了分析，讨论了标准器安装倾斜或偏心引入的误差分量、传感器测头安装偏心引入的误差分量以及测量仪器的线性漂移引入的误差分量等误差源对测量结果的影响，指出主轴偏心运动与测头安装偏心的耦合性[53]。2008年，彭万欢等人对超精密空气静压主轴回转误差测试过程中标准器的偏心进行了研究[54]，并设计了偏心调整装置，使安装偏心控制在1 μm以下；采用两点法误差分离技术，对比圆度仪测量结果，指出消除偏心只能采用消一次谐波分量的方法，不能用最小二乘法。同样地，徐秀玲等人从消除安装偏心为出发点，通过光学测量系统对主轴的误差运动进行测量，基于此文建立的模型分离出测试件的安装偏心[55]。

2011年，Lu等人对当下主轴计量中存在的一些问题提出了质疑。在现行的主轴计量标准中，位移传感器所测得信号中的基波分量仅仅被当作是标准器安装偏心引起的误差分量，而径向回转误差中的基波分量则被忽略不计。课题组讨论了此前主轴运动分析方法的局限性，证明径向误差运动中存在基波，提出了一种二维方法对主轴的径向误差进行分析及实验验证[56-57]。他们所采用的测量手段与2.1节中所提到的大多数方法并无二致，具体测量结构如图11所示。

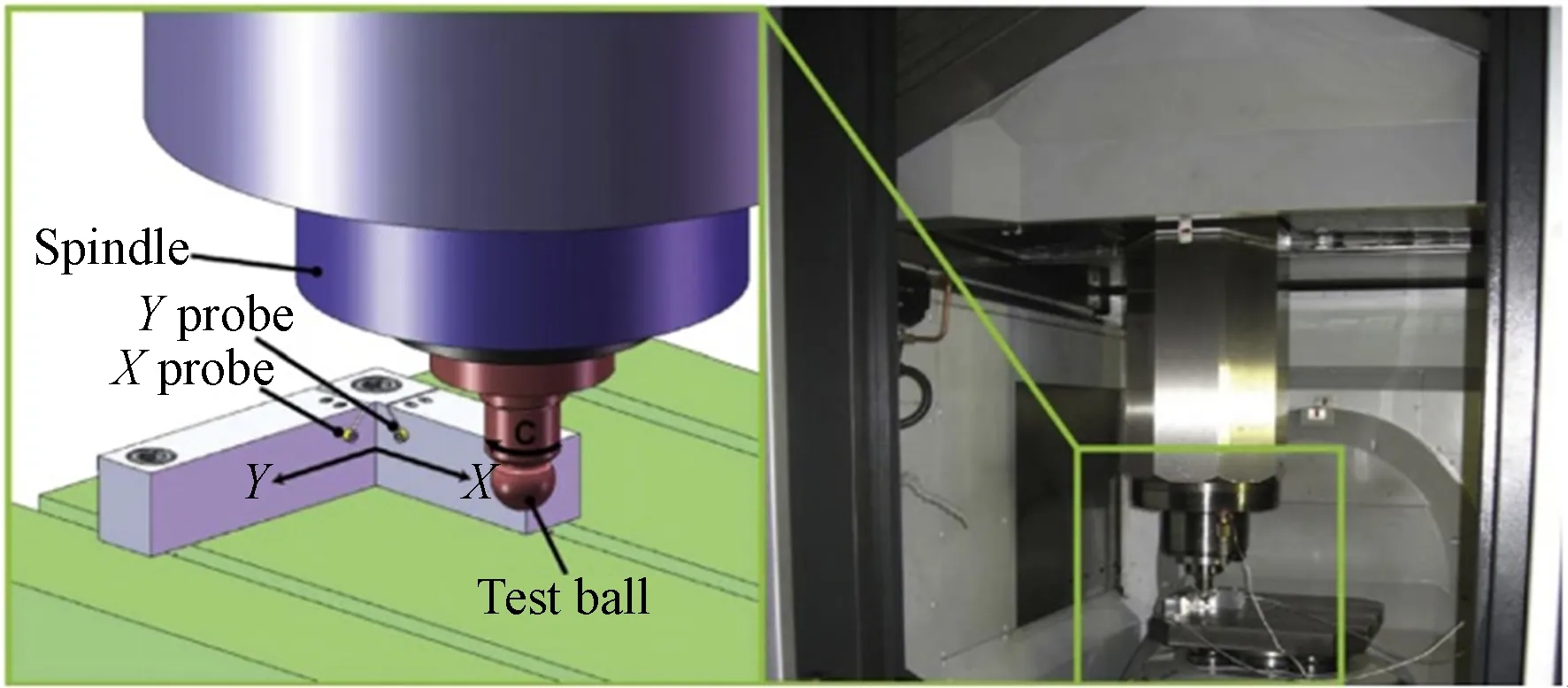
图11 基于二维分析法实现机床主轴回转误差测量[57]Fig.11 Measurement of spindle error motion based on two-dimensional analysis method[57]

除此之外，Shu等人对测量过程进行了完整的误差分析，分析了电容式位移探头的非线性误差、探头的对准误差、工件球的偏心误差、环境误差以及由不同的误差分离方法引起的误差[58]。课题组通过实验研究了针对球形表面的电容式位移探头的非线性，发现探头相对于标准球的横向偏移而导致的探头输出会极大地影响测量精度。

3.2 误差信息的应用

2013年，刘启伟分析了主轴测量中常规的测量误差组成、回转误差的产生原因及它对加工精度的影响，还进行了机床主轴回转精度测量方法及回转误差的评定[59]。主轴回转过程中的3种跳动对加工件的影响如表1所示。

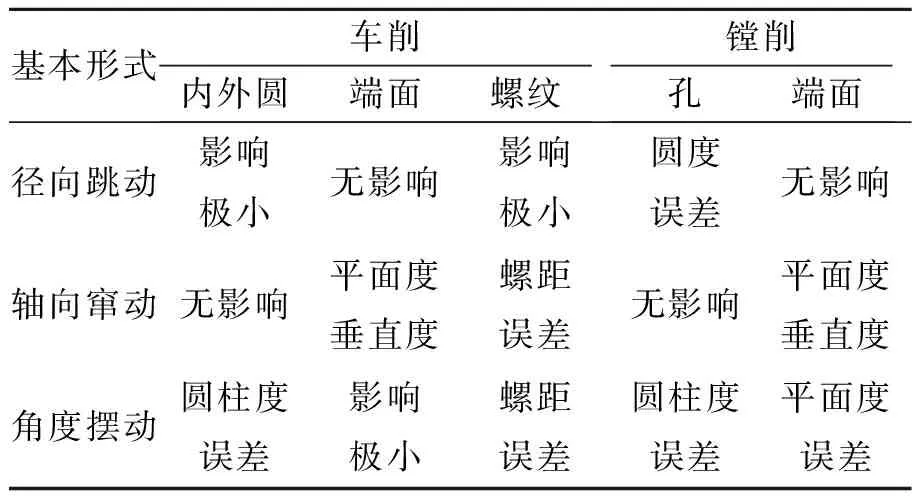
表1 机床主轴回转误差产生的加工误差Tab.1 Machining errors due to machine spindle rotation errors

2015年，Lee课题组研究了空气静压轴承主轴误差运动对加工精度的影响[60]。考虑了不平衡效应，课题组建立了空气静压轴承主轴动力学模型来表征由不平衡引入的主轴误差运动及其动力学行为。课题组还特别设计了一系列凹槽车削实验来研究由不平衡引入的主轴误差运动。实验结果和理论之间取得了良好的一致性，结果证实了空气静压轴承主轴误差运动存在低频包络现象，该现象被认为是主轴振动中两个运动分量在高频下的独特叠加效应。实验结果还表明，空气静压轴承主轴的旋转轴和刀尖之间的相对距离会随着主轴转速的不同而变化，从而极大地降低了加工精度。2016年，Lee课题组又对超精密金刚石车削中空气静压轴承主轴平均轴线位置的漂移进行研究[61]。他们在理论推导和实验验证的基础上研究了空气静压轴承主轴的主轴平均轴线的位移特性，并建立了主轴轴线回转过程中的误差模型用以分析导致慢刀伺服辅助车削中切削深度误差的原因。课题组还进行了微结构制造实验，以研究加工过程中沿圆柱形工件的轴向和径向方向的微结构的形貌误差。此外，课题组还对主轴误差运动进行了分析，研究了主轴不平衡引起的偏心距和热误差对主轴平均轴线位置漂移的影响。结果表明：由于流体动力作用，主轴平均轴线的位置漂移随主轴转速的变化而变化，并且漂移大小与主轴转速之间的关系是非线性的。

4 基于靶标轨迹追踪的主轴回转误差测量方法

在前人研究的基础上，本文提出一种基于靶标轨迹追踪法(Target Trajectory Tracking，TTT)来测量高速电主轴的动态径向回转误差。该方法采用工业相机和自制的靶标式标准器作为核心器件来测量主轴的动态径向回转误差。

4.1 靶标轨迹追踪法测量原理

基于靶标轨迹追踪的测量原理如图12所示。自制靶标式标准器被固定在待测主轴的回转端面，为了保证主轴高速运行时的动平衡，应使标准器回转中心与主轴中心轴线高度重合。工业相机被用来采集靶标轨迹图像，为了减小成像镜头边缘处光学畸变对测量结果的影响，应使镜头的光轴与主轴回转轴线高度重合。自制靶标式标准器由硅基靶标片、高亮LED及其他配件构成。硅基靶标片为具有微小通孔的厚硅片，通孔尺寸为10 μm，通孔下方装有高亮度LED进行照明，LED由纽扣电池进行供电。由于通孔尺寸极小，且距离相机较远，因此被LED照亮的通孔可以视作点光源，亦称作靶标。

图12 靶标轨迹追踪法测量原理Fig.12 Principle schematic of target trajectory tracking measurement

由于标准器被规定在主轴回转端面，因此标准器的运动特性与主轴保持一致。由于靶标为标准器上的一点，因此其运动特性也与主轴保持一致。当靶标随着主轴回转一周，其运动轨迹包含主轴轴线径向回转误差的所有信息，因此可以通过采集该信息来评估主轴的径向误差。

CCD的曝光时间由相机快门控制，在数十微秒到数十秒内进行调节。高速电主轴的回转周期大多为数毫秒或数十毫秒，因此通过外部触发的方式调整相机快门时间与主轴回转周期一致。完成上述配置后，可以采集到如图13所示的靶标随着主轴回转一周的轨迹。由于原始图像对比度极低，无法分辨靶标轨迹，图13为经过图像增强后的靶标轨迹图像。

图13 CCD采集的靶标轨迹Fig.13 Target trajectory captured by CCD

基于获得的靶标轨迹(图13)，主轴径向回转误差分析主要包括以下步骤：

(1) 通过图像预处理技术提高靶标轨迹的信噪比。假设主轴的运转速度为6 000 r/min，所使用的CCD像素为10 μm，靶标伴随主轴的回转线速度为3 m/s，则单个像素的曝光时间约为0.03 ms。因为曝光时间极短，导致CCD的输出响应极低。由于CCD自身的暗电流噪声和环境杂散光干扰，图像信噪比进一步降低。大量实验表明，本课题使用的装置在无靶标照明的情况下，由CCD暗电流噪声和杂散光影响导致的图像背景噪声灰度值约为10～16。为了减小背景噪声的影响，我们将电平裁剪法应用于原始图像。然后，对图像进行全局线性变换，进一步增强图像的对比度。

(2) 轨迹分离。在设计硅基靶标片时，在距离圆心5 mm的圆周上均布了4个靶标孔，由于靶标片的圆心与主轴回转轴之间存在偏心，因此CCD采集到的靶标轨迹图像中会出现多个靶标轨迹，如图13所示。因此，需要提取出每个靶标孔的轨迹图像，并做后续处理。由于每个靶标孔的回转特性都与被测主轴保持一致，因此多个靶标孔可以用来单独进行主轴径向回转误差评定。

(3) 靶标轨迹中心提取。对4条轨迹图像分别使用Canny算子进行边缘提取。经过Canny算子运算后，靶标轨迹的内外两侧的边缘如图所示。评价主轴径向回转误差需要使用靶标轨迹的中心信息。

图14 Canny算子边缘提取Fig.14 Image for Canny edge detection

(4) 评估亚像素靶标轨迹的圆度。参照ISO/TS 12181-1:2007，基于最小二乘参考圆对靶标轨迹进行圆度评估。首先求取靶标轨迹的最小二乘参考圆。经上述步骤求取的靶标轨迹可由坐标集P表示。P=[xi，yi]，i=1,2,3，…，n。n为靶标轨迹上数据点的个数。根据最小二乘法原理，目标函数可描述为：

(1)

对F(a,b,c)求偏导，令偏导等于零，获取极值点，得到：

(2)

求解上述方程可得a,b,c。进一步可知最小二乘参考圆的圆心O坐标为 (Xo，Yo)，半径为Ro，即有：

Xo=-0.5a，

Yo=-0.5b，

(3)

然后求取靶标轨迹上距离参考圆的最大和最小差值。Ri为数据集P中每一点到参考圆圆心O的距离，如公式(4)所示：

(4)

Ri与Ro的差值用来描述轨迹上的点与参考圆之间的距离，并以此求取Emax和Emin。

Ei=Ri-Ro,

(5)

Emax=max(Ei),

(6)

Emin=min(Ei).

(7)

Eround被用来描述最终的靶标轨迹圆度误差，则有：

Eround=Emax-Emin.

(8)

4.2 测量误差分离

基于4.1所描述的靶标轨迹追踪法，进一步分析了该方法对主轴回转过程中轴向回转误差运动和倾角回转误差运动对测量结果的影响。

4.2.1 轴向回转误差

测量装置装配时要求成像镜头的光轴与主轴的平均回转轴线重合,靶标固定在主轴上。当主轴回转运动中仅仅包含轴向误差运动Δδ时，靶标将形成如图15中的靶标轨迹，红色虚线为靶标最大轴向跳动时所在的平面。由于成像系统与主轴回转轴线同轴安装，因此CCD对靶标的轴向位移不敏感，所获取的轨迹图像不包含任何轴向误差运动的信息。

图15 靶标轨迹追踪法中的轴向误差Fig.15 Axial error motion in TTT method

4.2.2 倾角回转误差

建立模型以区分径向误差运动和倾角误差运动。靶标轨迹追踪法中的径向误差运动模型及CCD记录的轨迹如图16所示。图中，Δμ是以LSCI定义的径向回转误差，Ro是靶标轨迹上距离最小二乘参考圆圆心最远的点到圆心的距离，Ri是靶标轨迹上距离最小二乘参考圆圆心最远的点到圆心的距离，Δμ是Ro与Ri的差值，即靶标轨迹的圆度误差。

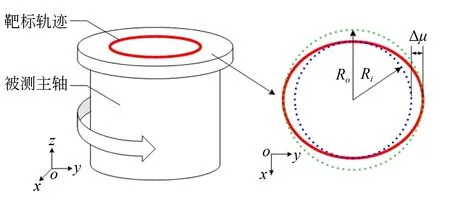
图16 靶标轨迹追踪中的径向回转误差与它的轨迹Fig.16 Radial error motion in TTT method

然而，当主轴仅以倾斜误差运动旋转时，CCD所拍摄的轨迹如图17所示，与图16中右图所示的轨迹相似。类似地，建立了靶标轨迹追踪法中的倾角回转误差运动模型。在这种情况下，Δμ′表示的不是径向回转误差，而是倾角回转误差表现为径向误差的形式。因此，需要对Δμ′与Δθ的数值关系进行分析。

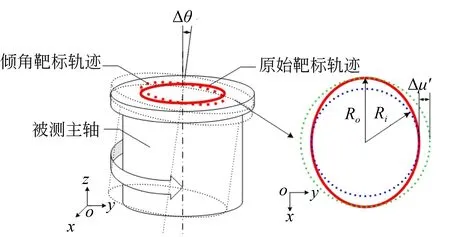
图17 靶标轨迹追踪中的倾角回转误差与它的轨迹Fig.17 Tilt error motion in TTT method

为了描述Δθ和Δμ′之间的关系，在图18中给出了另一个模型。图中，θM和θN是主轴回转过程中，旋转轴和主轴回转平均线之间的最小倾角和最大倾角。

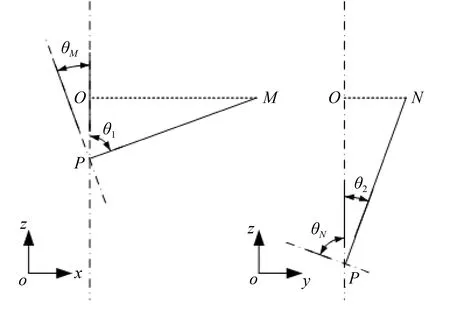
图18 倾角回转误差的定义Fig.18 Model of tilt error motion

因此，倾角回转误差Δθ可以定义为:

Δθ=θN-θM.

(9)

因为旋转面垂直于旋转轴，θM和θN可表示为:

(10)

因此，式(9)可以转换成:

(11)

根据这些定义，当靶标位于位置M时，可以假设靶标轨迹中没有倾角回转误差。这意味着，|MO|=|MP| = |NP|，θM= 90°。Δθ仅由θ2引起。 所以，Δθ可以表示为:

Δθ=90°-θ2.

(12)

结合上述方程，可以得到Δμ′和Δθ之间的关系:

Δμ′=MO-NO=MO·(1-cos Δθ).

(13)

假设主轴以5′倾角误差回转，而MO是5 mm，因此，Δμ′仅仅为5.29×10-6mm(即5.29 nm)。因此，可以忽略靶标轨迹追踪法中的倾角误差运动。靶标轨迹的圆度误差可以被认为是主轴的径向回转误差。

4.3 主轴动态回转误差测量实验

旋转轴是被测高速主轴的核心部件，由静压气浮支撑，实验过程中以500 r/min的步长实现500 r/min至6 000 r/min的速度。 通过超精密装配技术实现机械约束，将主轴的最大径向偏移限制在15 μm以下。对于正常工作状态，主轴的径向回转误差将不大于15 μm。实验中，将研制的标准器安装在被测主轴回转端面上。

测量设备如图19所示，测量基台由气浮底座支撑以减小外部振动对测量结果的影响。为了减小测量工作的计算成本，测量过程中使用1倍成像镜头实现1∶1靶标轨迹成像。所用CCD相机为JAI公司的BM 500GE，其分辨率为2 456×2 058，像元尺寸为3.45 μm×3.45 μm，成像芯片可以完全记录靶标轨迹。相机的快门时间可以从20 μs到2 s调整，当主轴转速为6 000 r/min时，可以调整快门时间至10 ms以记录主轴回转一周的轨迹。同时，为了实现对靶标轨迹的清晰图像，测量装置z方向设备要具有调节功能。相机的快门由外部触发器控制，严格地实现对主轴一次回转周期中的靶标轨迹获取。进一步地，由计算机来处理相机获得的靶标轨迹图像。

图19 基于靶标轨迹追踪法的测量系统配置Fig.19 Measuring device for TTT method

在实验数据评价过程中，用类似李萨如图的形式来描述主轴径向回转误差。基圆的半径为4个单元，每个单元的尺寸与像素(3.45 μm)相同。这些曲线是由数据集[xi，yi] 表示的长轴的角位置。与传统的基于标准球和电容传感器的测量方法不同，靶标轨迹追踪法得到的曲线没有标准器安装偏心误差，因此误差曲线的中心与基圆圆心重合。如4.2节中分析所述，测量误差即是主轴的径向回转误差。

为了评价靶标轨迹追踪法在高速下的测量稳定性，在高速主轴的工作速度为6 000 r/min时进行多组实验，结果如图20所示(彩图见期刊电子版)。根据4.1节中所述的主轴径向回转误差评定方法，绿色的内圆半径为Emin，红色的外圆半径为Emax。内外圆半径的差值表示Eround，分别为1.33，1.34，1.34，1.34，1.32，1.40 pixel，最大偏差约为0.08 pixel，即4.59，4.62，4.62，4.62，4.55和4.83 μm。最大偏差约为0.24 μm。由此可见，靶标轨迹追踪方法具有良好的稳定性。

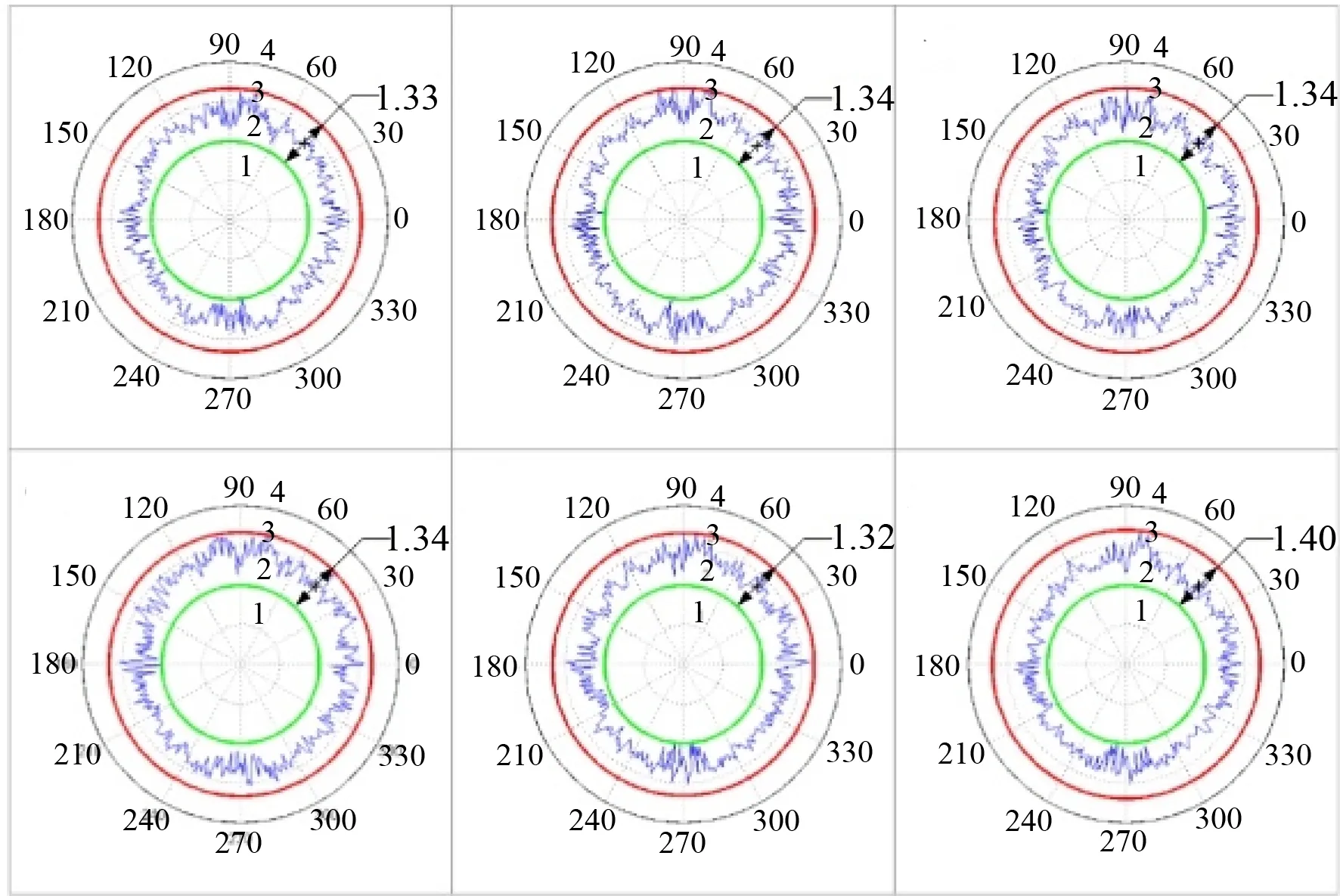
图20 高速主轴6 000 r/min时的李萨如图Fig.20 Lissajous images of radial error motion at 6 000 r/min

与此同时，在其他转速下测得的径向误差如图21所示。与6 000 r/min时的测量方法相同，在每个转速下获取15幅靶标轨迹图像。由图可见，当主轴低速运行时，靶标轨迹追踪法具有极好的测量稳定性。随着转速的增加，测量数据的离散程度逐渐增大，但是波动幅度小于0.2 pixel，即0.69 μm。若使用像元尺寸更小的CCD，可以获得更高的测量精度。

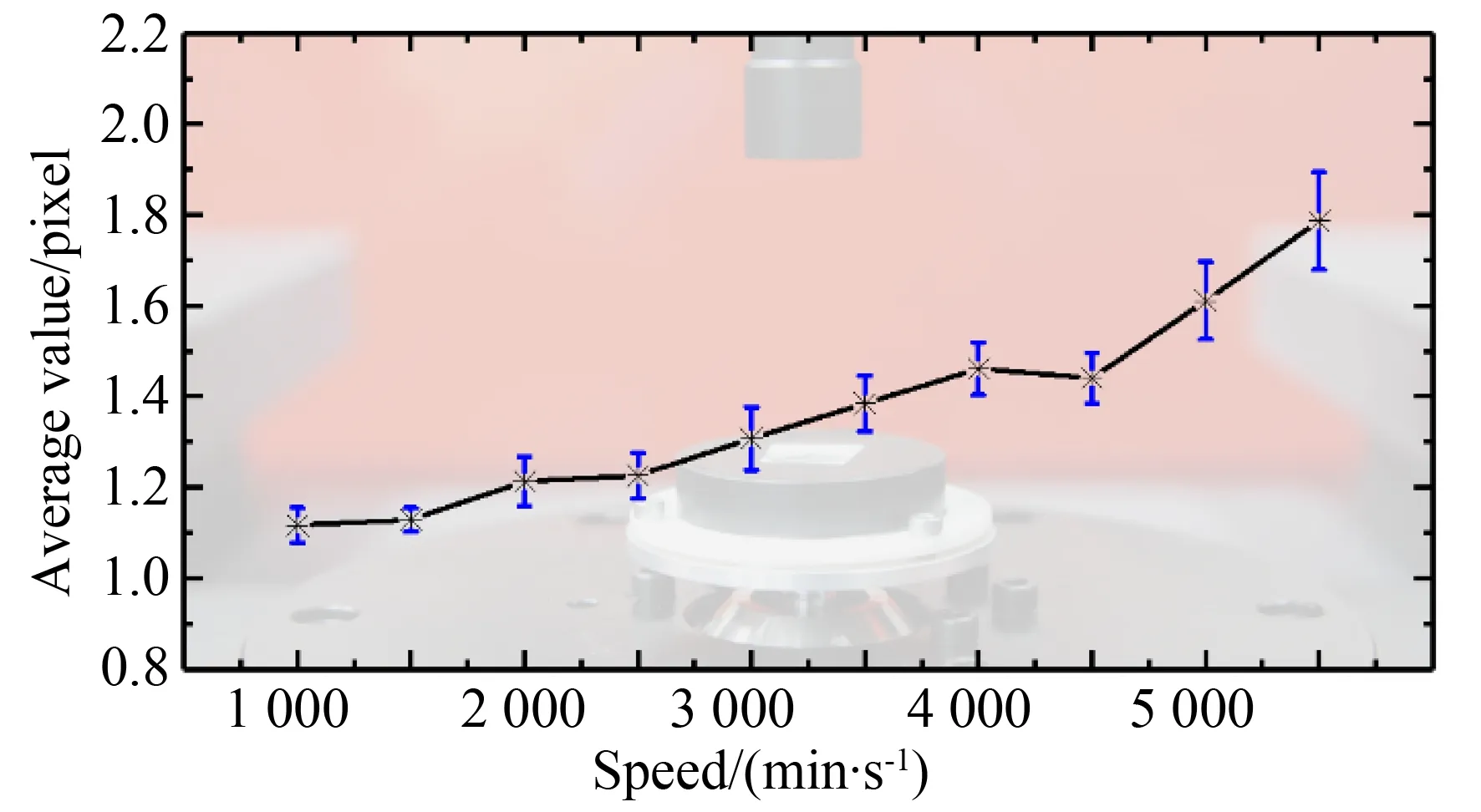
图21 不同转速下的测量结果对比Fig.21 Radial error of high-speed spindle at different speeds

通过上述分析可知，基于靶标轨迹追踪法通过评估靶标轨迹的圆度误差来测量高速主轴的动态径向误差，靶标轨迹的圆度误差等于主轴的径向回转误差。实验结果证实了所提出的靶标轨迹追踪法对6 000 r/min工作状态的主轴的动态径向回转误差测量的有效性。该方法结构简单、稳定可靠，可广泛应用于主轴动态径向误差测量领域。

5 总结与展望

本文对主轴动态参数计量技术的研究进行了分类与分析，从主轴回转误差测量方法和主轴回转误差测量数据的处理及使用两个方面进行了综述，并进一步提出一种基于靶标轨迹追踪法的主轴动态回转误差测量方法。

总的来说，国内外的回转误差研究从大圆成夫的三点法出发，对主轴静态/低速回转误差进行测量，不断改善测量方法，完善误差数据分离手段，已经形成了相当完善的测量体系。但是标准器的自身精度和安装精度，以及位移传感器自身的响应频率限制了这类方法在主轴动态参数计量中的应用。依托于光电技术的发展，一部分学者开发出了基于光学手段的主轴动态参数测量技术，有效地提高了测量精度，扩展了被测主轴的可测转速范围。由于光学手段依托于超精密光学装配技术，因此对光学系统的改进亟待进行。本文在总结前人研究的基础上，将超精密测量理论、误差分离与补偿技术、现代光电测量技术、数字图像处理技术等多学科交叉融合，提出了一种基于靶标轨迹追踪法的主轴动态回转误差测量方法，并实现了在主轴以6 000 r/min转速运行时的径向回转误差测量。实验结果表明：该测量方法的测量精度在微米级；单一转速的动态测量稳定性优于1 μm，对各个转速的动态误差测量都具有可靠性，满足了高速主轴动态参数测量的要求。