MNSR控制系统仿真研究

洪景彦，彭 旦，郝 倩，吴小波，李义国，王梦娇

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

微型中子源反应堆(MNSR)是一种以低浓铀(部分未低浓化的MNSR使用高浓铀燃料)为燃料、轻水作慢化剂、铍作反射层的罐-池式结构的小型低功率反应堆，功率约30 kW，最大热中子通量密度为1×1012cm-2·s-1。随着计算机运算速度的提高和计算机仿真技术的发展，控制系统的仿真变得越来越容易。对于研究堆这一具有一定不确定性的系统，应尽量减少在反应堆上进行热调试的时间。本文采用计算机仿真的方式对研究堆的控制系统进行研究，并对控制参数进行预整定。

1 数学描述及Simulink模型建立

通过对MNSR堆芯物理和MNSR闭环控制系统的研究，首先建立相关数学描述，在数学描述的基础上建立Simulink模型。主要包括描述MNSR堆芯物理的点堆动力学方程和闭环控制系统模型。

1.1 堆芯物理模型

描述MNSR堆芯物理的数学模型为点堆动力学方程[1-2]：

i=1,2,…，15

(1)

式中：n(t)为中子密度；ρ(t)为反应性；β为缓发中子有效份额；Λ为中子代时间；βi为第i组缓发中子有效份额；λi为第i组缓发中子先驱核衰减系数；Ci(t)为第i组缓发中子先驱核浓度。由于MNSR使用铍作为反射层，一般采用15组缓发中子建立点堆动力学方程，其中6组为普通缓发中子，9组为光致缓发中子。

1.2 闭环控制系统模型

MNSR闭环控制系统的原理框图如图1所示。

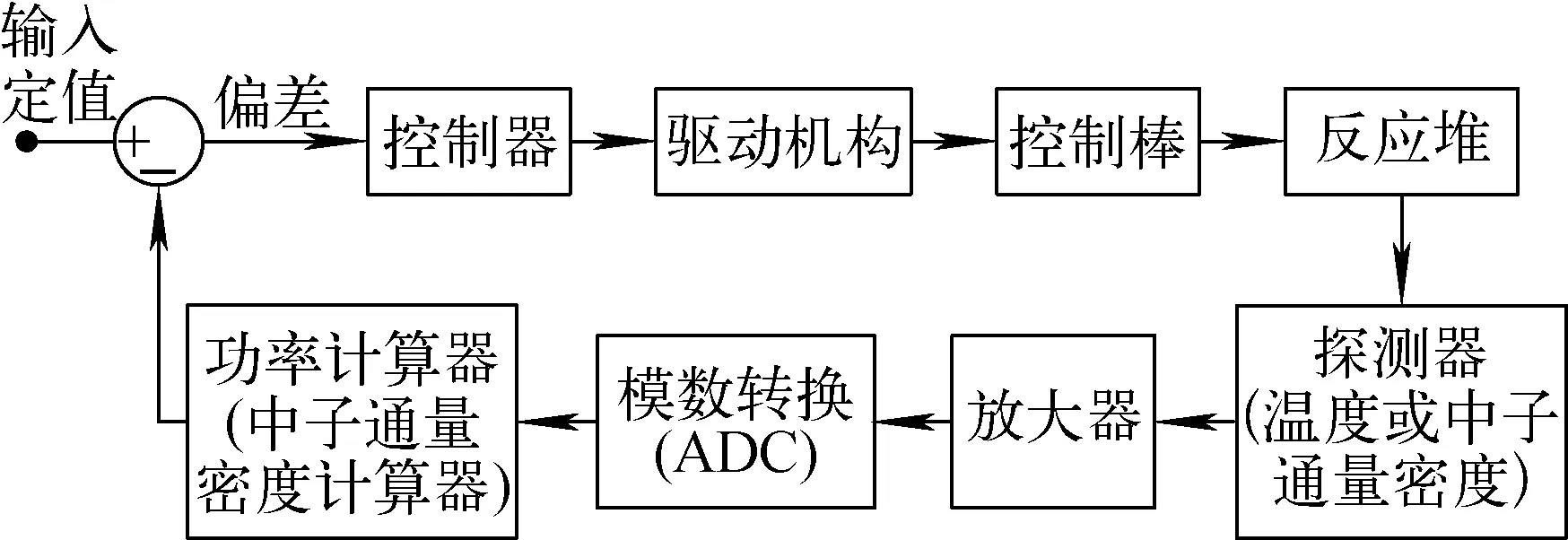
图1 MNSR闭环控制系统原理框图Fig.1 Diagram of MNSR close loop control system

1) 中子通量密度测量模型

中子通量密度的测量可等效为测量和模数转换(ADC)两个部分。中子通量密度测量可等效为一惯性环节，即：

Gd(s)=1/(Tcs+1)

(2)

而对于ADC可等效为一零阶保持器，即：

GAD(s)=(1-e-Ts)/s

(3)

式中：Gd(s)为一阶惯性环节的传递函数；Tc为时间常数；s为拉普拉斯变换的自变量；GAD(s)为AD转换器的传递函数；Ts为采样时间。

2) PID控制器模型

应用唑来膦酸后出现急性葡萄膜炎一般需要糖皮质激素治疗。本研究中1例患者首选给予眼部抗病毒及抗炎治疗，眼部症状恶化[16]，提示抗病毒及抗炎治疗通常无效。一般局部应用类固醇激素能使大部分病例的眼部症状完全缓解。如局部应用类固醇激素，患者眼部症状未明显改善，或患者急性葡萄膜炎始发症状较严重，可口服或静脉全身给予糖皮质激素治疗。另外，为解除睫状肌痉挛，改善局部血循环，减少渗出物，防止虹膜后黏连，可联合使用睫状肌麻痹滴眼剂[31]。

PID控制器模型为控制算法中最为经典的算法，其数学表达式为：

(4)

式中：e(t)为偏差；Ti为积分时间常数；Td为微分时间常数。

对上式离散后，得到离散的PID控制器模型为：

(5)

式中：P、I和D分别为比例、积分和微分的系数；z为离散传递函数的自变量。根据这一原理直接使用了Simulink中的离散PID控制器的仿真模型。

3) 交流伺服电机模型

交流伺服电机的运动方程[3]为：

(6)

式中：J为电机转动惯量；Tem为电磁转矩；B为黏滞摩擦系数；ωm为电机转速；Tl为负载转矩。

由于与电机的电磁转矩相比，负载转矩很小，可忽略，同时忽略摩擦带来的转矩损失，则可得：

(7)

因此，交流伺服电机可等效为一阶惯性环节，其传递函数为：

Gm=1/(Tems+1)

(8)

4) 控制棒驱动机构模型

MNSR的驱动机构主要采用减速箱，通过绳轮将交流伺服电机和控制棒连接，传动机构的数学模型为：

(9)

式中：S为控制棒位移；D为绳轮直径；α为减速箱减速比；n为伺服电机转速。由上式可得，传动机构可等效为积分环节，其传递函数为：

Gmc=1/s

(10)

5) 控制棒模型

由反应堆物理的基本原理可知，控制棒的反应性价值为一个S形曲线。MNSR的控制棒价值通过零功率实验实际测量，并对测量值进行多项式拟合可得控制棒释放的反应性与控制棒位的关系为：

ρ(l)=-1×10-9l4+2×10-7l3+

9×10-5l2+2.6×10-3l+0.195 8

(11)

综上分析，利用Matlab的Simulink工具箱，建立了MNSR控制系统仿真模型，如图2所示。

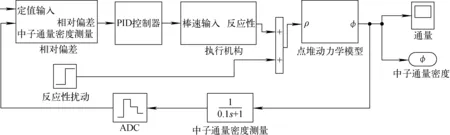
图2 MNSR闭环控制系统仿真模型Fig.2 Model of MNSR close loop control system

2 仿真分析

建立Simulink仿真模型后，对MNSR闭环控制系统进行了仿真分析[4-6]，主要包括稳定性分析、PID控制器参数整定分析和负阶跃反应性输入及斜坡反应性输入分析。

2.1 稳定性分析

在MNSR运行过程中，仅考虑中子通量密度平稳运行的因素，因此仅需估计系统增益和采样时间的大致范围，因此，在稳定性分析之前，仅需建立MNSR控制系统的简化模型。图3为MNSR控制系统简化模型原理图。

简化后的闭环传递函数为：

C(s)=Gr(s)N(s)/(1+Gr(s)H(s))

(12)

式中，H(s)=KpGd(s)Gm(s)K，为反馈传递函数。对开环传递函数进行Z变换后得到离散开环传递函数：

G(z)=Z[Gd(s)Gm(s)KRGr(s)]

(13)

由于Gr(s)的阶次很高，为分析带来很大麻烦，需对其进行降阶处理。利用Matlab的模型降阶工具箱，对Gr(s)进行降阶，降阶后的传递函数为：

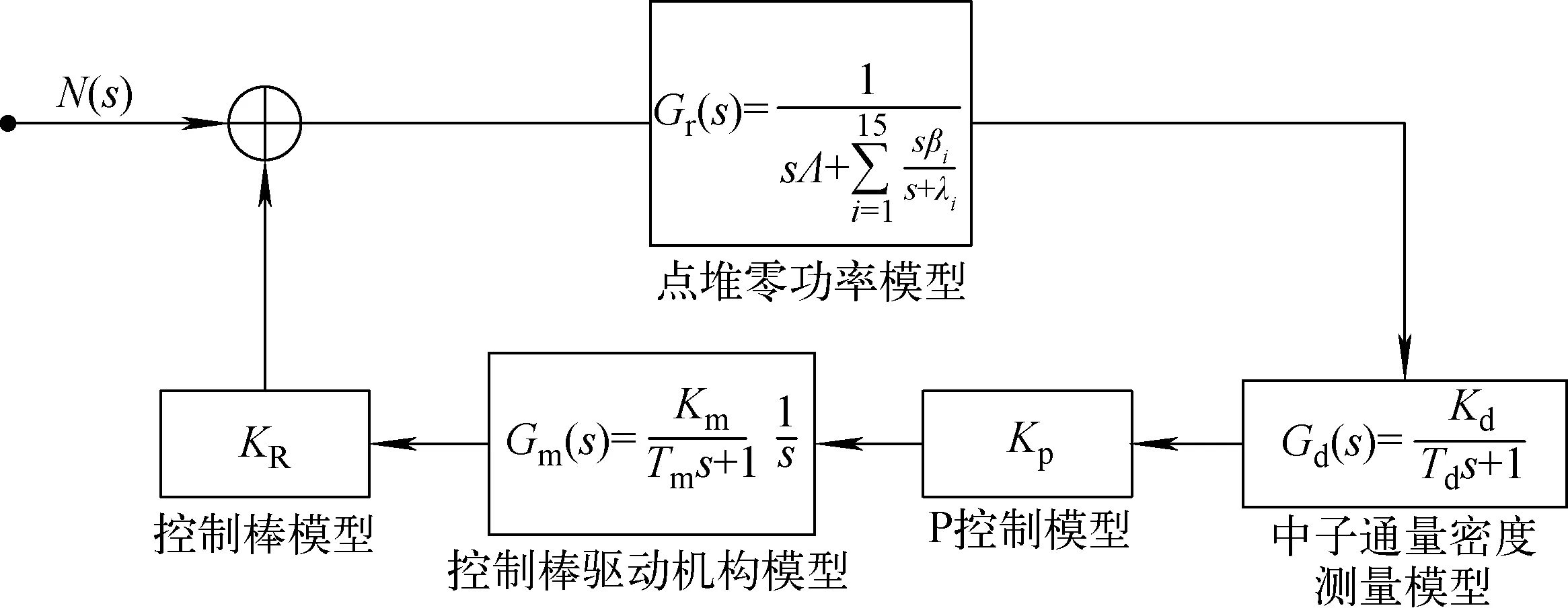
图3 MNSR简化闭环控制系统原理图Fig.3 Diagram of simplified MNSR close loop control system

G′r(s)=

(14)

则离散后的传递函数为：

G′(z)=Z[Gd(s)Gm(s)KRG′r(s)]

(15)

对离散开环传递函数(式(15))使用Matlab的rltool工具后即可得到系统的根轨迹，如图4所示。

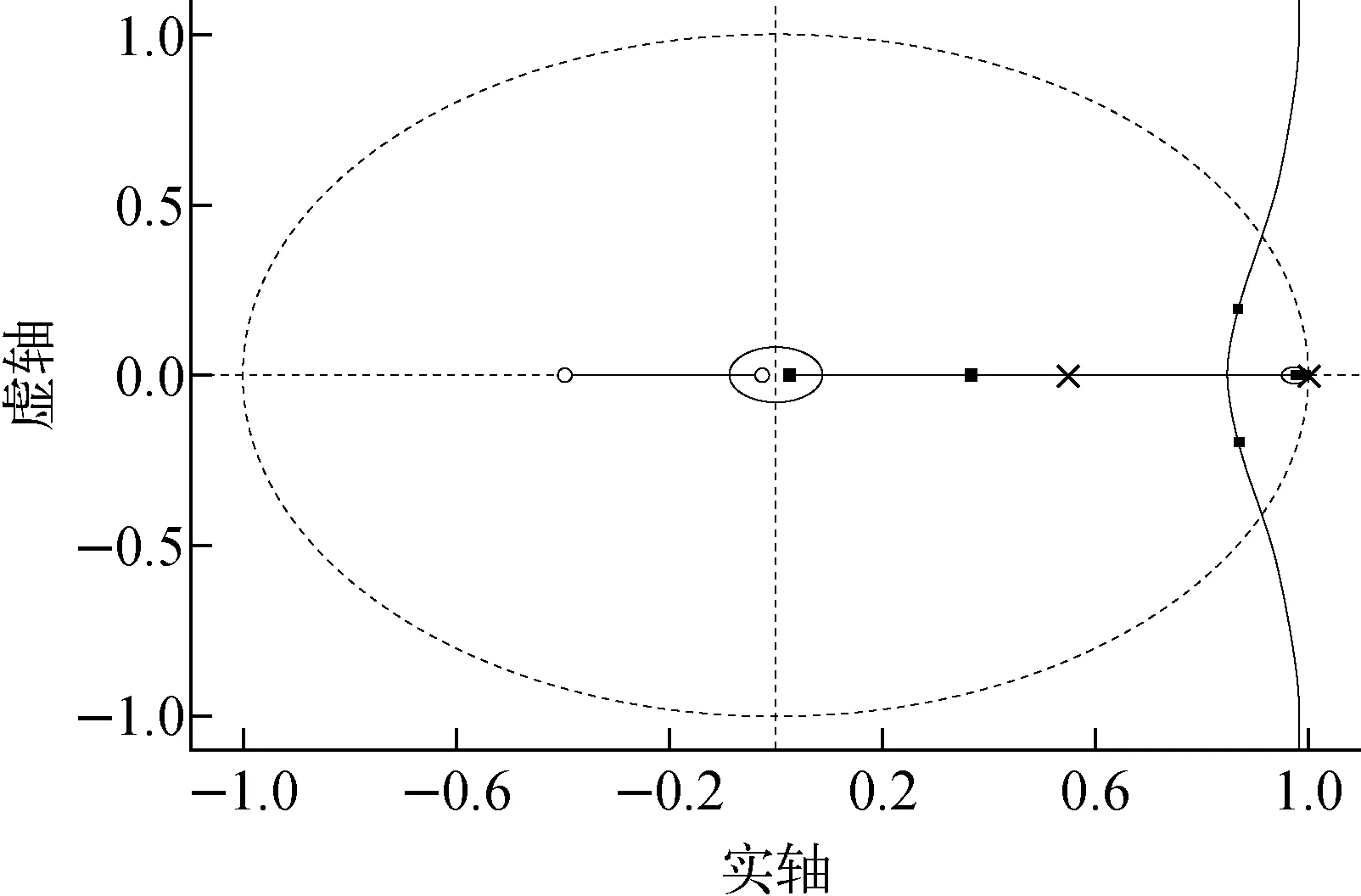
图4 采样时间为60 ms时MNSR离散系统的根轨迹Fig.4 Root locus of discrete system of MNSR at sampling time of 60 ms

利用根轨迹工具箱的编辑功能即可得到当前采样时间下的临界增益。表1列出不同采样时间下的临界增益。从表1可看到，随着采样时间的增加，临界增益减小，这说明，采样时间增加，增益的裕度越小，系统的稳定性越差。

2.2 PID控制器参数整定

通过稳定性分析后，对系统的增益有了基本的认识，在此基础上，选取不同的采样时间Ts，对比例系数Kp进行整定[7-10]，整定的目标为中子通量密度的超调小于8%，调整时间在7 s以内，最多出现1次振荡(这一要求比较适合MNSR的实际应用)。

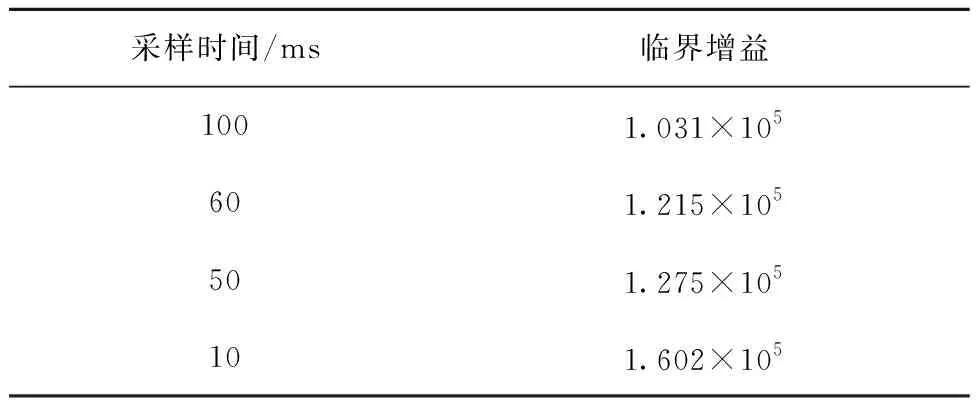
表1 采样时间与临界增益的关系Table 1 Relationship between sampling time and critical gain

综合考虑各种因素后，分别选择采样时间为100 ms和60 ms时，进行参数Kp和Kd的整定，经过多次的仿真整定后，确定了最佳的参数为Ts=60 ms、Kp=2 500、Kd=300，该组参数兼顾了系统的快速性、超调量和电机寿命等因素。图5为稳态情况下0.5 mk阶跃反应性输入时中子通量密度的变化。

图5 0.5 mk阶跃反应性输入时中子通量密度响应Fig.5 Neutron flux density response with 0.5 mk reactivity insertion

2.3 负阶跃反应性输入及斜坡反应性输入响应

系统整定完成后，分别进行了负阶跃反应性输入(这符合MNSR样品辐照时引入反应性的实际情况)和斜坡反应性输入(这符合MNSR缓慢放入具有正反应性效应样品的实际情况)响应[11-15]。图6为-0.5 mk阶跃反应性输入的中子通量密度响应和PID控制器的输出及控制棒速度响应。

图7为斜坡反应性输入的中子通量密度响应和PID控制器的输出及控制棒速度响应。

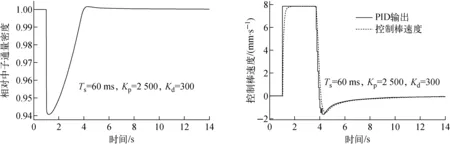
图6 -0.5 mk阶跃反应性输入时中子通量密度响应和PID控制器的输出及控制棒速度响应Fig.6 Responses of neutron flux density, PID controller output and control rod speed with -0.5 mk reactivity insertion

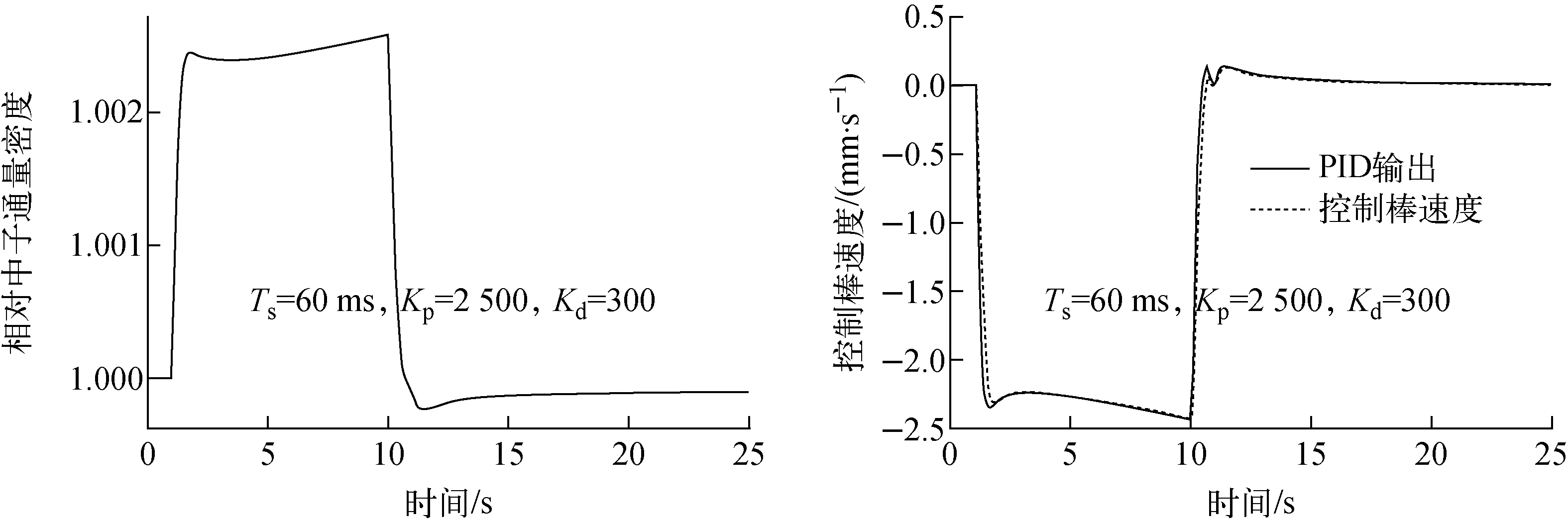
图7 引入斜坡反应性时中子通量密度响应和PID控制器的输出及控制棒速度响应Fig.7 Responses of neutron flux density, PID controller output and control rod speed with ramp reactivity insertion

3 结论

在点堆动力学基础上建立反应堆堆芯物理的数学描述和闭环控制系统各部分数学描述，结合Matlab/Simulink仿真技术建立了MNSR堆芯物理的Simulink模型和MNSR闭环控制系统的模型。

对MNSR控制系统进行了线性化、降阶和离散化，建立了MNSR离散化的开环传递函数，并对传递函数采用根轨迹方法进行了稳定性分析，得到了不同采样时间下控制系统的临界增益。

在稳定性分析的基础上进行了PID控制器参数的整定，得到了1组最佳整定参数Ts=60 ms、Kp=2 500、Kd=300时的仿真结果。在最佳整定参数下，分别仿真了负阶跃反应性输入和斜坡反应性输入响应。仿真结果表明，整定参数能满足MNSR运行要求。参数整定值及系统的仿真参数为MNSR控制系统的软硬件设计提供了理论基础和指导作用，能大幅降低MNSR控制系统的开发难度和减少开发周期，降低系统设计成本。