API X65深水海底管道J形铺设横向焊接变形

李明朝，李光泉，周灿丰，陈智，周珍珍

(1.中石化胜利石油工程有限公司钻井工艺研究院，山东 东营 257017；2.中石化石油工程技术服务有限公司，北京 100000；3.北京石油化工学院，能源工程先进连接技术研究中心，北京 102617；4.哈尔滨焊接研究院有限公司，哈尔滨 150028)

0 前言

海底管道铺设采用的方法主要包括卷筒铺设、S形铺设和J形铺设。J形铺设通过垂直铺管架将管道送到海底，下放过程中管道呈大写字母J形。当水深超过1 500 m时，J形铺设与S形铺设相比具有铺管船结构紧凑、推进器功率要求低等优点[1]。因为J形铺设在深水具有突出竞争优势，在工程中得以迅速发展，其相关研究也相当活跃[2-10]。

J形铺设因为铺管架上的管道长度达到48～72 m而且处于垂直位置，背面不加衬垫，属于横向位置单面焊接双面成形[11]。海底管道对焊接质量有严格的要求，有一系列相关标准对其进行了规定[12-14]，焊接变形是多道焊面临的主要问题之一，而这个问题对于J形铺设窄坡口、横向位置单面焊接双面成形而言更是应该重视。SYSWELD是在考虑材料力学性能与温度有关的焊接热弹塑性分析理论的基础之上发展的焊接专用软件，其主要支撑理论包括Goldak等人[15]开发的双椭球热源模型描述GMAW焊热源，以及Leblond等人[16]开发的相变模型。文中依托焊接应力与变形分析理论，在SYSWELD软件中以焊缝截面平均热循环曲线作为加载热源，采用二维截面有限元模型进行了API X65管线钢钢板横向多道焊焊接变形与应力仿真，开展了焊接变形试验验证，研究表明仿真果大致吻合试验结果，多道焊的最终焊接变形主要取决于前面几道焊缝。

1 焊接应力与变形分析理论

瞬态热输入的高度集中对整个焊接过程及焊后工件带来大量的焊接残余应力及变形。焊接数值模拟是一个非线性问题，主要是几何非线性和材料非线性，但是由于有限元法在空间上的离散作用，求解焊接应力场就变成了计算材料非线性的瞬态问题。

1.1 米塞斯屈服准则

米塞斯(Von Mises)屈服准则的原理是金属材料若发生塑性变形，则单位体积内的变形能须累积到一定临界值，该值只与材料有关，而与应力状态无关。根据文献[17]，其判断式为方程(1)。

(1)

式中：σ1，σ2，σ3是三维空间三个正交方向的主应力；σs是单向拉伸时的屈服极限。

材料进入屈服极限后继续若继续加载，这时的应变增量则分为两部分：一是弹性应变增量{dξ}e，一是塑性应变增量{dξ}p，等效应变定义为方程(2)。

(2)

式中：εx，εy，εz为空间里三个正交方向的主应变；μ为泊松比。

1.2 热弹塑性理论

热弹塑性分析法通过实时求解温度场来计算热应变与应力，是研究焊接应力与应变的主要方法。对于瞬态热分析，可将温度梯度值最大的时间节点温度作为载荷分析结构应力，考虑材料在不同屈服状态下温度场对应力应变结果的影响。

根据文献[18]，材料热弹塑性的应力应变关系用矩阵的形式表示为方程(3)。

{dσ}=[D]{dε}-{C}dT

(3)

式中：[D]为弹塑性矩阵；{C}为温度相关相量。

对于计算模型中的某一单元，其平衡方程为方程(4)。

{dF}e+{dR}e=[K]e{dδ}e

(4)

式中：{dF}e是单元节点力增量；{dR}e是由温度变化导致的单元初始应变等效节点力增量，{dδ}e为节点位移增量，[K]e为单元刚度矩阵。

2 API X65管线钢板横向焊接应力与变形数值仿真

2.1 焊缝截面平均热循环曲线的提取

焊接热循环曲线是一条温度-时间变化曲线，表征节点在一个完整的焊接过程之中，温度上升和下降历程。在焊接数值仿真中，它既是三维单元模型单道焊仿真的结果，也可以作为二维单元截面模型多道焊仿真的热源型式。如图1所示，在SYSWELD软件中，提取焊接热循环曲线的方法是：完成三维单元模型焊接仿真模拟后，选取一个截面的节点，以温度为纵坐标、时间为横坐标建立坐标系，显示如图1a包含所有焊缝节点的一系列曲线，利用Display面板的Averaging命令求出该组曲线的平均曲线，如图1b所示，然后将该平均曲线作为二维单元截面模型多道焊仿真的加载热源。

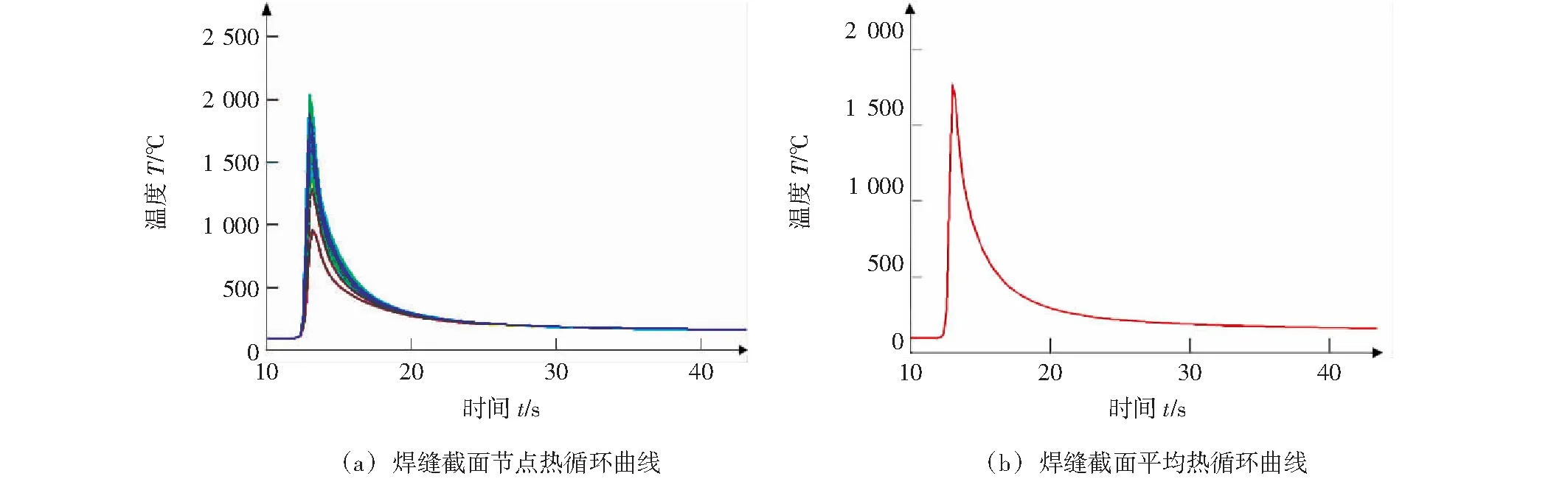
图1 热循环曲线

2.2API X65管线钢板材多道焊焊接工艺参数

APIX65板材外观尺寸为300 mm×60 mm×17.8 mm，坡口为海底管道铺设中常用的机加工窄坡口，其参数如图2所示，该坡口的优点是焊接效率高、填充量小、焊接热影响区窄。图3是该板材的三维模型。前期研究中，进行了板材与管道整圆的六分之一部分的焊接温度场对比研究，二者材料、厚度、坡口参数相同，二者焊接温度场数值计算结果高度一致。所以，如果采用相同的约束条件，则二者焊接变形的趋势应该是一致的。当然，如果是完整的管道，则还需进一步的研究。

图2 焊接坡口图

图3 三维模型

多道焊是一个对焊缝循环冷却和加热的过程，随着层间温度的升高，焊缝t8/5时间变长，导致晶粒粗化，焊接接头质量降低。综合考虑焊接效率和焊接接头性能、选择层间温度为150 ℃，观察焊接热循环曲线可知对应层间间隔时间为60 s。焊接工艺是熔化极气体保护自动焊，焊接位置为横向，焊接工艺参数见表1。

2.3 多道焊数值仿真

2.3.1约束条件

采用ESI公司的前处理专用网格划分软件Visual environment进行模型网格划分，板材横截面网格如图4a所示，其特点是起弧和收弧阶段焊接热流密度变化较大，因而网格划分较密。板材通过压板施加约束，在SYSWELD软件中的表达如图4b所示。通过二维截面来模拟和分析焊件横截面的变形，压板约束的特点是约束点的应力大大增加，变形为零，离约束位置越远则变形越大。

表1 焊接工艺参数

图4 横截面网格及约束条件(mm)

2.3.2多道焊变形仿真

采用SYSWELD焊接向导设置焊接工艺及其多道焊模块设置焊接间隔时间及计算方法进行多道焊仿真[19]。通过后处理云图显示，将每道焊接后的截面图如图5及图6所示，自由端最大变形值演变曲线则如图7所示。

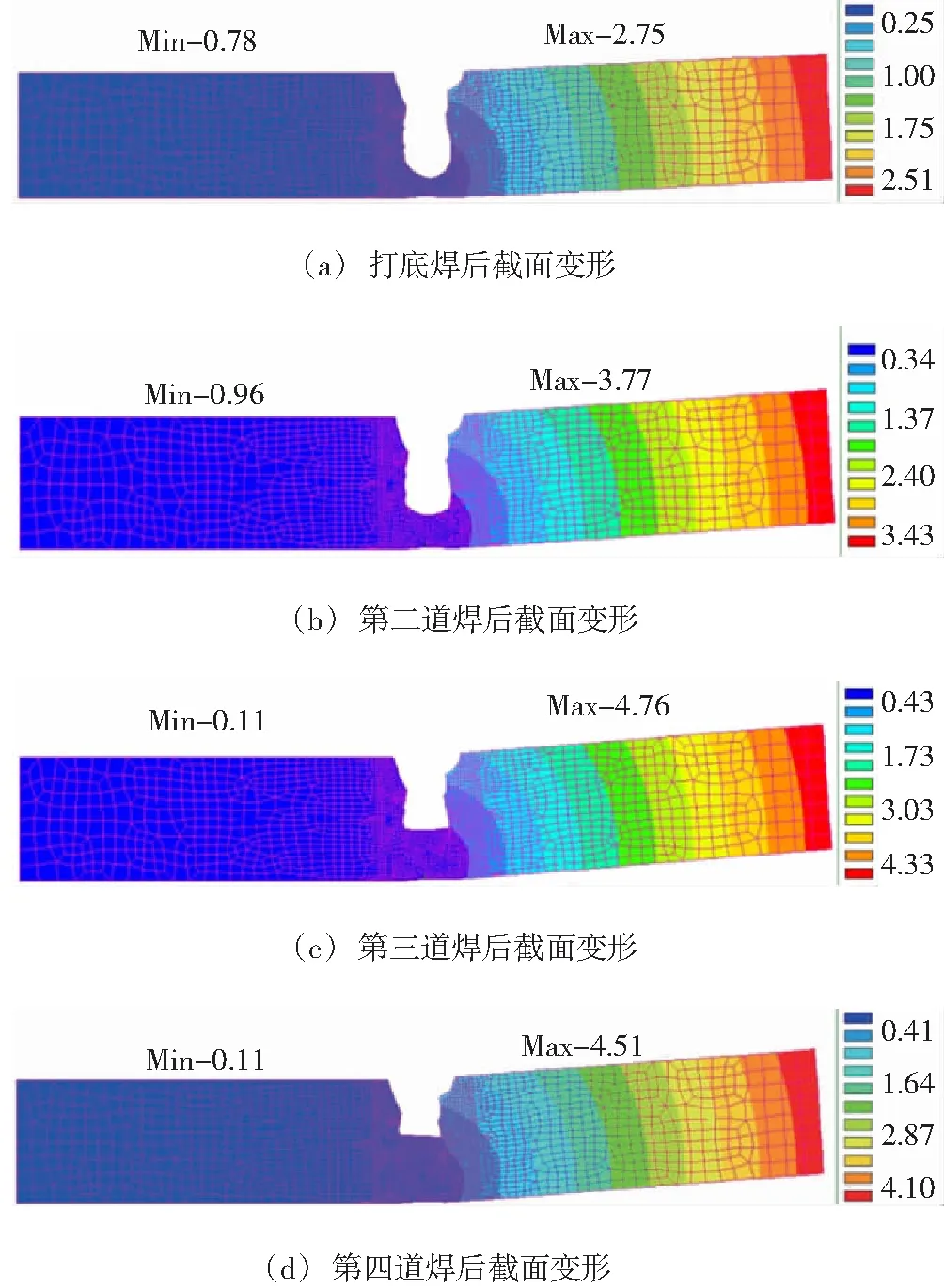
图5 打底焊后至第四道焊后的变形(mm)

图7 焊接变形曲线

2.3.3多道焊应力仿真

通过后处理云图显示，多道焊残余应力分布如图8所示。

图8 不同时间平均残余应力分布(MPa)

3 API X65管线钢板材横向焊接试验

横向焊接试验系统如图9所示，焊接电源是TPS4000数字化焊接电源，自动焊接小车通过与直线导轨的啮合而在处于垂直位置的焊接变位机上实现水平移动，板材通过快速夹具固定在焊接变位机上。

采用与数值仿真相同的API X65管线钢钢板、相同的多道焊焊接工艺参数。焊接完成之后选择焊件自由端最下方节点为参照点，该点对应于SYSWELD软件仿真中的编号为34154的节点，实测其变形量为5 mm，如图10所示。

图9 横向焊接试验系统

图10 横向多道焊钢板焊接变形

4 讨论

API X65管线钢钢板GMAW横向多道焊最终焊接变形实测值为5 mm，计算值为图6h所示的4.41 mm，误差为14%，模拟结果大致吻合试验结果。存在的误差主要原因：①焊接试验中横向焊接热流分布因为熔池向下流淌而与SYSWELD仿真中的均匀分布假设不符合；②二维截面模型的计算精度不够；③焊接试验中的约束是有间隔的数个夹板固定而不是SYSWELD仿真中的整块夹板固定；④热循环曲线法比移动热源法的热输入小。

二维截面有限元模型可以定量计算多道焊变形结果，在多道焊焊接过程中，前面几道焊缝对最终焊接变形影响大，而后面几道焊缝影响小。根据图6所示的焊接变形仿真结果，第一层的变形最大值是2.75 mm，第二层为3.77 mm，第三层为4.76 mm，焊接完成后的变形是4.41 mm。前三层基本决定了整个变形的大致轮廓与数值，后面几层的变形影响相当小，甚至有时随着焊缝道数的增加变形反而减小的情况。

焊接最终变形分为两部分：一是在焊接过程中产生的基础变形；二是焊件中残余应力释放产生的变形补偿。根据图8所示的焊接应力仿真结果，可以发现在自由端没有残余应力，而在焊缝中心、热影响区和过渡区都是受到较大的残余拉应力、而释放这些残余拉应力会促使材料从焊缝中心向外挤，从而抵消焊接的基础变形。在前几层焊接中，焊接的基础变形大，残余应力释放引起的变形补偿不明显。在后几层焊接中，已填充的焊缝改变了结构的整体刚度，对焊接的收缩变形有缓冲作用，基础变形减少，而由残余应力释放产生的变形补偿就比较明显地抵消了一部分焊接变形。

5 结论

(1)以焊缝截面平均热循环曲线作为加载热源，采用二维截面有限元模型可以定量计算多道焊变形结果，模拟结果大致吻合试验结果。

(2)横向多道焊模拟结果与试验结果之间存在的误差，主要因素包括热流分布、二维截面模型的计算精度、约束及热循环曲线自身特点。

(3)在多道焊焊接过程中，前面几道焊缝对最终焊接变形影响大，而后面几道焊缝影响小。

(4)在多道焊焊接过程中，前几层焊接中焊接的基础变形大，后几层焊接中由残余应力释放产生的变形补偿明显地明显地抵消了一部分焊接变形。