基于增维细胞传输模型的区域管制空域容量评估

高 伟， 康道驰

(中国民航大学空中交通管理学院， 天津 300300)

在中国民航近30年的持续高速发展过程中，经空域规划与管制技术的不断升级完善，北京、上海、西安等中国繁忙机场的终端区空域通行能力大幅提升，机场容量的运行瓶颈已逐渐转移至终端区所在区域管制空域的接收能力。为了改善空域资源供给与利用，需要对区域管制空域的运行服务能力即区域容量进行评估。

涉及区域容量的研究主要分为空中交通流量管理、拓扑结构、交通流复杂度和危险天气影响4个方面。

空中交通流量管理主要以延误、安全成本与容量为目标对区域流量进行优化。Bayen[1]利用拉格朗日算法分析了航路容量和交通流延误问题，并利用混合整数线性规划(mixed integer linear programming，MILP)算法给出了优化后的方案，提出繁忙空域交通流量欧拉网络模型和基于空中交通流量管理的拉格朗日延迟模型来计算区域容量。Chen等[2]基于动态空中交通流构建航路网络模型，采用对偶分析法求解以运行花费最小作为目标函数，以区域容量作为限制条件的混合整数线性规划问题，从而实现对区域交通流的优化。Hossain等[3]提出空域容量与安全风险折中计算模型，计算在可接受的安全风险下的区域扇区最大容量。

拓扑结构主要从航路网络复杂度分析和航路网络结构两方面进行研究。网络复杂度分析主要将航路网络抽象为拓扑网络，使用复杂网络理论对航路网络拓扑结构进行分析。描述复杂网络的特征量主要包括度、权、平均路径长度、簇系数、度分布、介数等。陈才龙[4]提出一种空域容量的多目标粒子群优化方法，通过复杂网络建模，给出了空域容量的一种定量描述方法，最后采用多目标粒子群算法得到了航路汇聚点布局问题的非支配解。航路网络基本结构的研究主要包括航路交叉点个数及位置、航段长度、航路交叉角度等与航路网络容量间的关系。Wang等[5]在航路网研究的基础上考虑了限制区、危险区、禁区的限制因素，通过对交叉点的合并与位置改变实现对航路网结构优化，并基于元胞自动机思想求解该模型。

交通流复杂度方面，Song等[6]提出了基于交通流模式识别的空域容量预测方法，考虑交通流属性和管制员的管制策略因素，对未来30 min到几小时内的空域动态容量进行预测，但并未探讨交通模式与容量之间的关系，以及不同时间尺度内的交通流模式的预测方法。

危险天气方面，Mitchell[7]研究了在确定的空域范围和给定的恶劣天气影响下的容量算法，并且分析了天气对容量的影响；Krozel等[8]考虑恶劣天气和各种运行条件进行了航路容量评估。

现基于区域航路网络拓扑结构对研究区域容量采用细胞传输模型将区域航路网中每条航线分为若干细胞，将时间离散化为若干时段，以细胞容量作为限制条件，以容量最大作为目标函数构建MILP模型，通过遗传算法对该模型进行求解。通过与TAAM仿真软件的对比来验证该模型的准确性。

1 细胞传输模型

1.1 细胞传输模型概述

细胞传输模型(cell transmission model，CTM)是运动学模型LWR(lighthill，whitham and richards)模型差分离散形式[9]。经过十几年来的发展，中外不少学者对其进行了进一步研究和完善，CTM 已经成为模拟路网中的动态交通流传播，研究交通流运行规律的有效工具。将细胞传输模型引入空中交通，并对其进行增维处理，加入高度维对区域空域网络进行建模。

1.2 定义

图1所示为区域航路航线网络图，区域航线网络分为若干高度层，每一高度层上的二维航线网络由航线、区域边界和航路点构成。

1.2.1 点

点包括转弯点、航线与航线的交叉点及区域边界与航线的交点，用P表示。在图1中共有10个点则P={P1,P2,…，P10},其中P2、P6表示转弯点；P3、P9表示航线交叉点；P1、P4、P5、P7、P8、P10表示区域边界与航线的交点。

1.2.2 边

边分为航段与区域边界线。航段为航线上两点之间的部分用L表示。在图1中共有9个航段则L={L1,2,L2,3,L3,4,,L8,9,L9,10,L5,9L9,6L6,3,L3,7}。以L1,2为例表示点P1与点P2之间的航线部分，其方向为从点P1到点P2，航段方向与所在航线方向一致。航线由航段组成，用R表示，航线分为经由区域进出终端区的航线和通过区域空域但不经过终端区的飞越航线两类。在图1中共有3条航线，R={R1,R2,R3}。其中以航线R1为例，航线R1由航段L1,2、L2,3、L3,4组成，R1={L1,2,L2,3,L3,4}，其方向为P1→P2→P3→P4。区域边界为所选定区域空域的边界线在图1中以粗实线表示。

1.2.3 高度层

区域管制空域为三维空间，分为若干高度层，每个高度层上的二维航线网络均相同。高度用H表示，图1中共有3个高度层，H={H1,H2,H3}。

图1 区域空域航线网络图Fig.1 Regional airspace route network diagram

1.2.4 细胞

将每个航段按区域管制间隔分为若干细胞，用C表示。细胞作为组成航线网络的最基本单元C={C1,C2，…，CN}，N表示航线网络中细胞的总个数。图2以航段L1,2为例将航段L1,2分为n个细胞每个细胞长度为区域管制间隔。由于航段长度与区域管制间隔并非整数对应关系，所以要对每个航段的最后一个细胞长度进行取整保留。

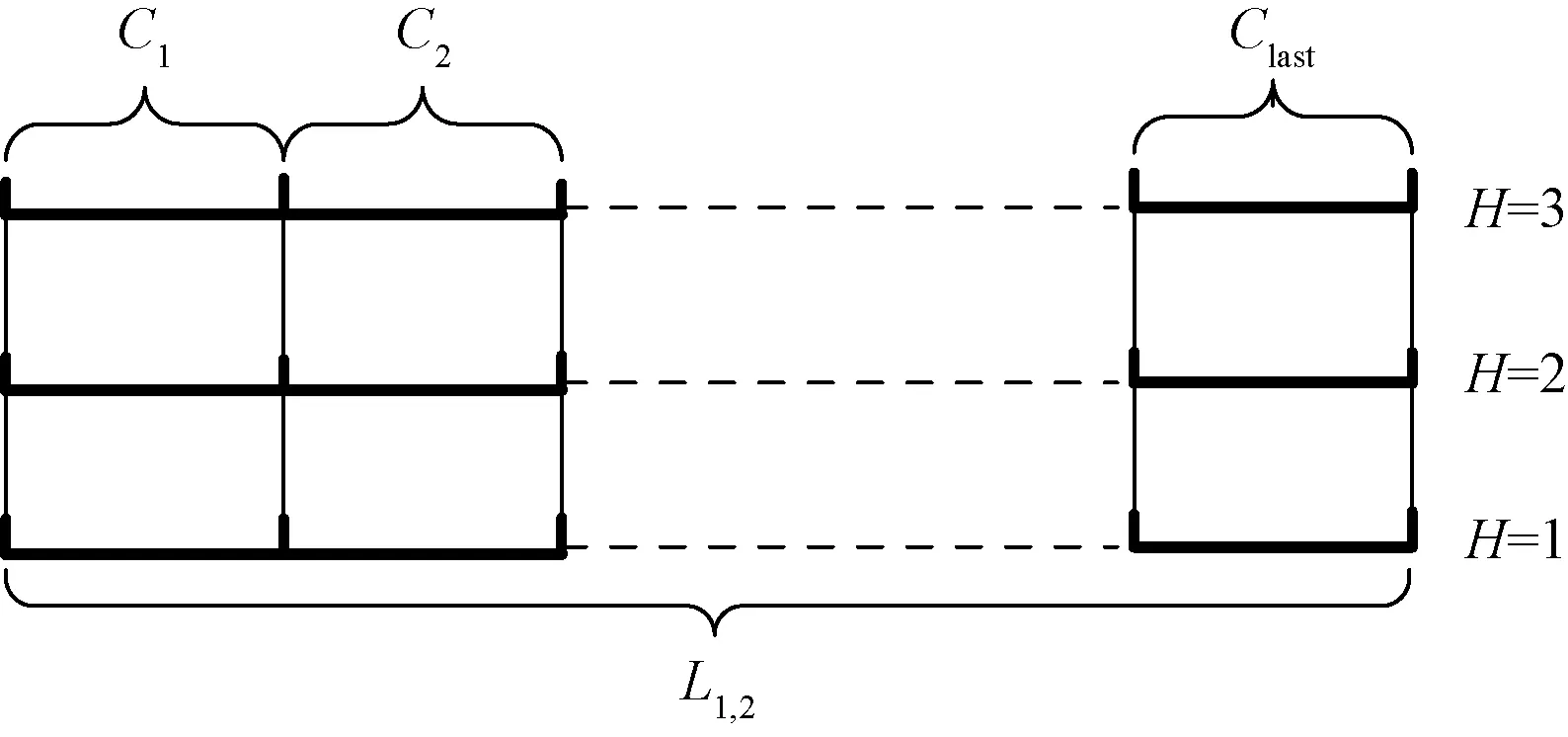
图2 航线细胞结构图Fig.2 Diagram of route cell structure

(1)

式(1)中：n表示航段L1,2上细胞的个数；DL1,2表示航段L1,2的长度；Dcontrol表示区域管制间隔。

(2)

式(2)中：Clast表示位于航段L1,2上最后的细胞，其中Clast∈{C1,C2，…，CN}；DClast表示细胞Clast的长度。

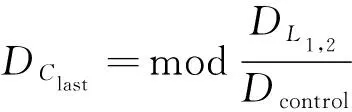
(3)

式(1)中的n为四舍五入后的取整值，当航段长度与区域管制间隔相除的小数部分小于0.5时，航段上最后一个细胞Clast的长度如式(2)所示，反之取式(3)。每个高度层上的细胞分布均相同。

1.3 飞行速度分析

根据雷达数据分析，影响航空器飞行速度的主要因素为高度层与航段位置。如图3所示，通过对同航段不同高度层上的航空器速度分布进行对比，航空器速度每个高度层上呈正态分布，但高度层不同，速度的均值与方差也不同。如图4所示，在相同高度层的不同航段上航空器的速度分布依然呈正态分布，航段不同，正态分布的参数也不同。

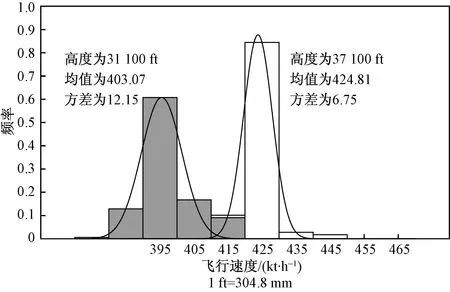
图3 不同高度层速度分布Fig.3 Velocity distribution at different levels

图4 不同航段速度分布Fig.4 Velocity distribution of different sections

通过以上分析可知，航空器的飞行速度在各航段各高度层上均呈正态分布，即各航段各高度层上航空器的飞行速度大部分落于某一速度区间之内，以正态分布的均值作为航空器的飞行速度，不会造成过大的计算误差，满足精度的要求。由于正太分布均值与方差随高度层和航段位置的变化而变化，速度变量将由航空器所在细胞的航段位置及高度所决定。

1.4 细胞传输模型构建

1.4.1 模型假设

(1)航空器在细胞内的飞行速度为恒定值，速度由细胞所在航段位置及高度决定。

(2)将时间离散化，以分钟作为时间单元进行计算。

(3)模型不考虑天气等随机因素的影响。

(4)区域飞越航线以平飞为主不发生高度层的改变，进出终端区航线会发生高度层的改变。

(5)航空器需要改变高度层时，航空器从细胞的起始端开始高度变化在完成一个高度层跨越时其飞行的水平距离为一个细胞的长度，如图5所示。航空器在改变高度时其水平速度取该细胞所在两个高度层速度的平均值。航空器不在交叉点处发生高度层改变。

图5 航空器高度层改变示意Fig.5 Elevation level change of aircraft

1.4.2 模型变量计算

1.4.2.1 飞越细胞时间

航空器飞越细胞所用时间由细胞所在航段位置及高度层决定。

(4)

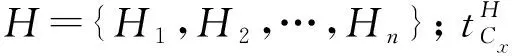
1.4.2.2 进入区域交通流

以1 min为时间单元对进入区域的航空器进行标定。

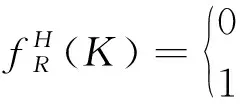
(5)

1.4.2.3 高度层

每一架航空器都将生成一个高度层矩阵，高度层矩阵表示航空器在航线的每个细胞上飞行所使用的高度层。高度层矩阵的维度为高度层数×航线细胞数。

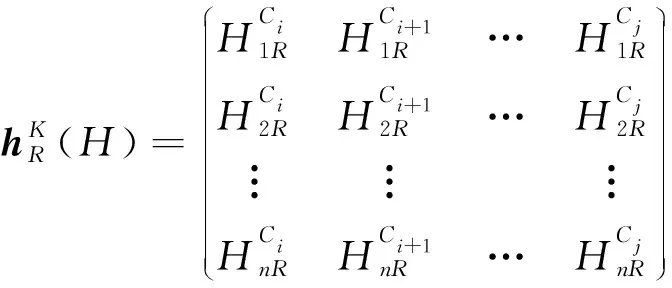
(6)

1.4.2.4 进入细胞时间

当式(5)的值为1时航空器进入细胞时间取决于细胞所在位置及进入区域空域时间。

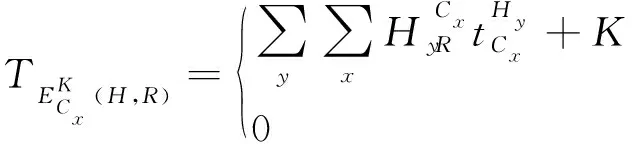
(7)

式(6)中高度矩阵为0的元素进入时间均为0，表示航空器不从该高度层进入该细胞。

1.4.2.5 离开细胞时间

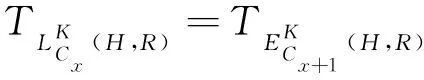
(8)

1.4.2.6 交叉点间隔

交叉航线可以看作由多个转弯航线构成，求解交叉点间隔则转化为求解转弯点间隔。转弯点示意图如图6所示。航空器F1到达转弯点P1时航空器F2距航空器F1的距离记为d。当航空器F1通过点P1时两航空器之间的距离可以表示为

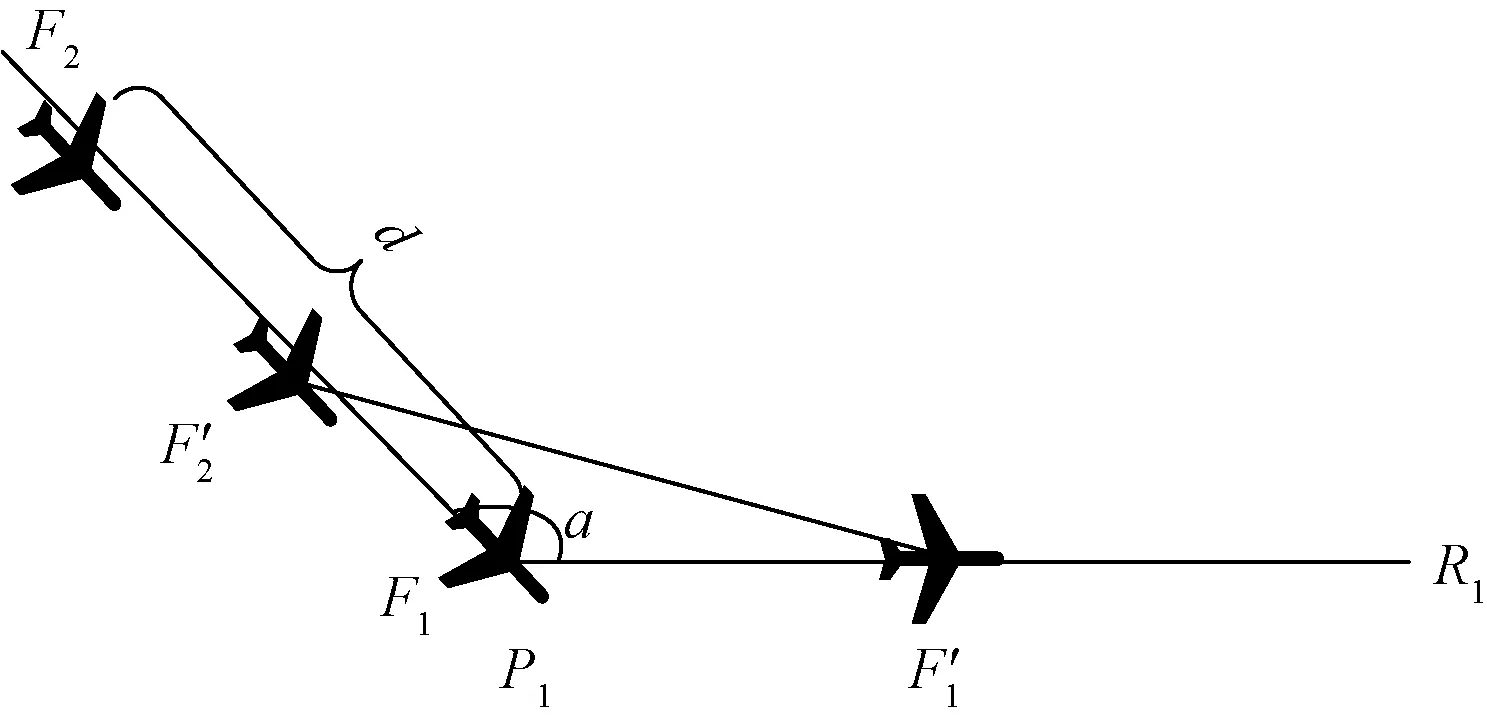
图6 转弯航线示意图Fig.6 Diagram of turning course

(9)

式(9)中：dF1-F2表示航空器飞过P1点后两航空器之间的距离；时间t以航空器到达点P1时记作0；a为两航段的夹角；vF1、vF2为两航空器速度，其数值等于航空器所在细胞的速度。

通过对式(9)求导求解两航空器之间的最小值，令最小值等于区域管制间隔。通过对导数为零与最小值等于区域管制间隔两式联立解出d。

(10)

过点P1的时间间隔为

(11)

交叉航线可以看作由多个转弯航线构成(图7)，其中交叉航线由n×n种转弯航线组合而成则交叉点间隔取转弯点间隔的最大值，如式(12)所示。

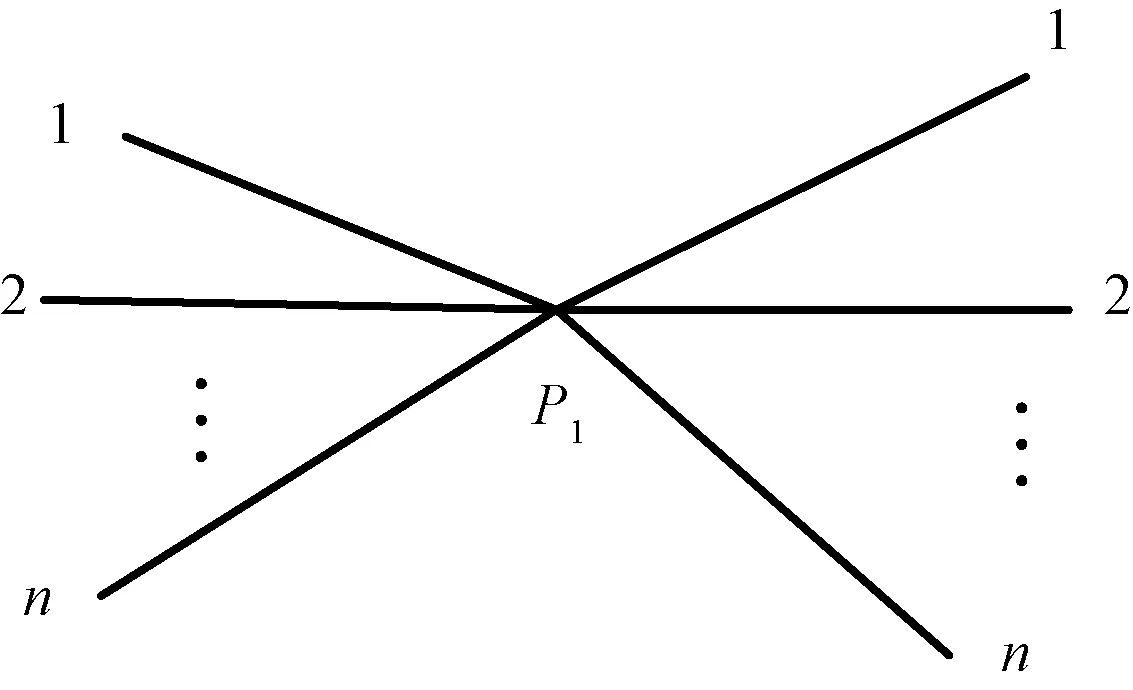
图7 交叉航线示意图Fig.7 Diagram of crossing route

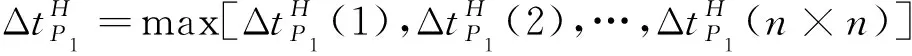
(12)

1.4.2.7 细胞通过量

1.4.2.8 扇区通过量

扇区作为区域空域的组成部分，将扇区通过量定义为给定时间内通过扇区的航空器数量，用Sx表示。

(13)

式(13)中：Sx表示给定时间内通过扇区x的航空器数；C表示扇区入口处细胞的集合；K为给定时间集合；H为高度层集合。

1.4.2.9 区域通过量

区域通过量与扇区通过量类似，表示给定时间内航空器通过区域空域的数量，用A来表示。

(14)

1.4.3 区域容量

由于以求解区域最大容量为目的，所以目标函数为一定时间内进入区域航空器数量最大。限制条件为细胞容量与交叉点间隔。由于细胞长度为区域管制间隔，所以所有细胞容量均为1。

(15)

限制条件：

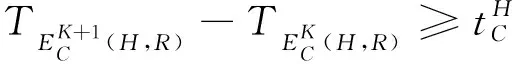
(16)

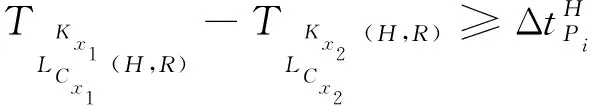
(17)

式(17)中：Pi为航路交叉点的总集合；Cx1、Cx2表示以交叉点Pi为细胞终点的细胞集合；Kx1、Kx2分别表示细胞Cx1、Cx2进入区域空域的时间。

式(16)表示相邻两架航空器后机进入细胞C前机进入细胞C的时间差大于细胞C的通过时间确保了细胞C的容量为1；式(17)则表示通过交叉点的时间差大于允许值。

2 遗传算法求解

2.1 遗传算法概述

遗传算法是模拟达尔文遗传选择和自然淘汰生物进化过程的计算模型[10]。该算法是一种基于生物自然选择与遗传机理的随机搜索算法，起源于对生物系统进行的计算机模拟研究，是自然遗传学和计算机科学相互结合渗透而成的算法。

与传统搜索算法不同，遗传算法[10-11]从一组随机产生的初始解开始搜索过程，该初始解称为种群(population)。种群中的每个个体是问题的一个解，每个个体由携带基因编码的“染色体”组成。遗传算法通过对初始种群的选择、交叉、变异运算筛选出最优个体，即为所求的最优解。

2.2 遗传算法构建

2.2.1 初始种群生成

(18)

式(18)中：G(R1)表示个体中航线R1基因序列，矩阵G(R1)中的每一行为个体的一个染色体，染色体的长度为给定时间段的长度Kn。

(19)

式(19)中：G表示个体的基因序列由区域空域中的每一条航线的基因序列组成。

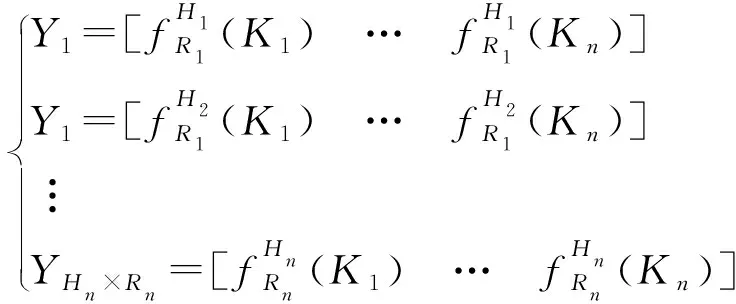
(20)

式(20)中：Y表示染色体。

个体中的染色体Y的数目为矩阵G的行数，即Hn×Rn。对生成个体进行检验使生成的个体需要满足式(16)、式(17)的限制条件，生成多个满足条件的个体构成初始种群。

2.2.2 适应度

适应度是在研究自然界中生物的遗传和进化现象时，用来度量某个物种对于生存环境的适应程度。对生存环境适应度较高的物种将获得更多的繁殖机会,而对生存环境适应程度较低的物种，其繁殖机会就会相对较少，甚至逐渐灭绝。本文中个体以给定时间内进入区域空域航班数的总和为适应度，如式(21)所示。

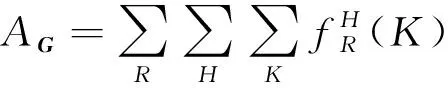
(21)

式(21)中：AG表示个体G的适应度。

2.2.3 选择

选择指决定以一定的概率从种群中选择若干个体的操作。一般而言，选择的过程是一种基于适应度的优胜劣汰的过程，本文中选择过程将采用基于适应度选择的轮盘赌算法，即适应度越大选择概率越高，原理类似于博彩游戏中的轮盘赌。个体选择概率为

(22)

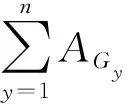
2.2.4 交叉

有性生殖生物在繁殖下一代时2个同源染色体之间通过交叉而重组，即在2个染色体的某一相同位置处DNA被切断，两染色体互相交换被分离的染色体片段后组成新的染色体。本文中采用单点交叉，由于单个染色体的长度为给定时间段的长度，所以交叉点的选取范围为(2,Kn-1)。图8所示为个体G1与个体G2的Y1进行交叉重组。

图8 染色体交叉示意图Fig.8 Diagram of chromosome crossing

2.2.5 变异

变异指染色体复制时可能(很小的概率)产生某些复制差错，变异产生新的染色体，表现出新的性状。本文中则表示个体中染色体上为0的基因以一定概率突变成1。

2.2.6 遗传算法总流程

3 算例

选取覆盖北京终端区的12个区域扇区作为研究对象，如图10所示，共有80个航路点、184个航段、636个细胞和153条航线其中134条通过区域航线，10条由区域进入终端区航线，9条从终端区进入区域航线。北京区域扇区的管制高度为7 800～12 500 m，按照东单西双原则向东的航线分为8 100、8 900、9 500、10 100、10 700、11 300、11 900、12 500 m共8个高度层，向西的航线分为7 800、8 400、9 200、9 800、10 400、11 000、11 600、12 200 m共8个高度层。

图10 选取区域空域示意图Fig.10 Diagram of selected regional airspace

3.1 计算结果

选取1 h为总时长，计算区域空域1 h的最大容量。所需参数：区域管制间隔为20 km，初始种群中的个体数为100交叉概率0.6，变异概率0.01。遗传算法经50次迭代后结果如图11所示。最终收敛的均值为884.52，即选定区域空域的小时容量为884架次。进入终端区和从终端区进入区域空域的小时架次116.54，通过区域空域的小时架次为767.98。

图11 适应度迭代曲线Fig.11 Fitness iteration curve

3.2 TAAM仿真验证

选择收敛后群体的一个个体作为样本生成时刻表，通过TAAM对该时刻表的仿真与CTM模型计算结果进行对比。表1为各扇区小时通过架次的比较，可以看出，交通流主要集中在12扇区、16扇区、17扇区和19扇区，总体上计算值要略高于仿真值。

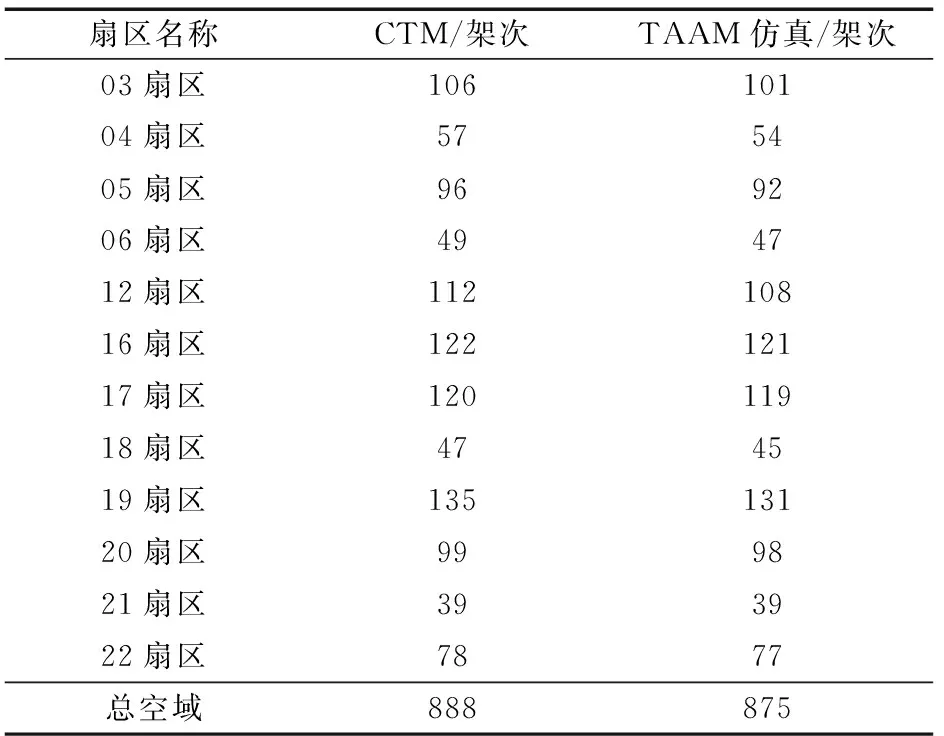
表1 扇区小时通过架次统计Table 1 Sector hour statistics

4 结论

采用增维细胞传输模型构建区域交通流MILP模型，利用遗传算法进行求解得到区域空域容量，取得了与TAAM基本一致的结果。这说明CTM适合区域交通流这种中观尺度的空域容量分析，且不需要购置昂贵的仿真平台，建模简单，只要给定区域空域结构，即可快速分析其容量，有助于分析区域空域对终端区进入区域航班的接收能力，从而对合理分析与规划机场容量提供重要决策依据。该模型只要将有关场景涉及的细胞部分稍作处理，还可以得到灾害性气象条件或军事活动影响下的区域管制空域容量。