基于Weibull分布的冻融循环下纤维混凝土损伤模型
张广泰, 刘诗拓, 耿天娇, 彭 瑞, 陈 勇
(新疆大学建筑工程学院, 乌鲁木齐 830047)
在北方寒冷地区,混凝土在冻融循环作用下经常产生弹性模量下降、强度衰减、表面剥落、基体开裂等影响混凝土耐久性的现象,从而引起建筑物破坏甚至倒塌[1]。因此模拟冻融地区混凝土耐久性试验研究尤为重要,如何减少在冻融循环下混凝土的损伤和预测服役期间混凝土结构耐久性是目前亟待解决的问题。
近年来,中外众多学者对冻融循环条件下混凝土的损伤劣化进行了大量的研究。肖前慧等[2]通过拟合数据建立了冻融循环下预测强度衰减模型。赵燕茹等[3]研究不同冻融介质对动弹性模量、质量损伤、力学性能的影响,建立了强度剩余模型。杜鹏等[4]建立了基于残余应变的冻融损伤模型。陈爱玖等[5]从冻融破坏机理出发,并基于Aas-Jakoben混凝土材料疲劳公式建立了普通混凝土冻融损伤模型。Tamon等[6]基于动弹性模量、质量损失率建立弹性模型,预测冻融循环下素混凝土的耐久性。黄伟敏等[7]、章文姣等[8]、陈柳灼等[9]通过在混凝土中单掺钢纤维和聚丙烯纤维,发现钢纤维和聚丙烯纤维的掺入有利于提高混凝土的力学性能和弹性模量,使混凝土破坏形式从脆性破坏转为塑性破坏,改善混凝土整体性,提高混凝土抗冻融性能。姚文杰等[10]基于数据拟合建立二次函数和指数函数表征聚丙烯纤维混凝土的冻融损伤,在拟合精度方面,二次多项式要优于指数函数。
目前,对于纤维混凝土冻融损伤研究多数为试验性研究,并且建立的损伤模型多为确定性模型,用简单的多项式拟合来反映纤维混凝土内部的随机损伤具有一定模糊性。现将Weibull概率分布引入纤维混凝土冻融损伤耐久性研究中,通过损伤变量、相对动弹性模量、相对强度之间的关系推导出两种冻融循环下纤维混凝土的损伤模型,从而完善冻融循环下纤维混凝土的耐久性理论,为寒冷地区实际工程的防灾减灾提供理论依据。
1 试验
1.1 原材料和配合比
水泥:P.O42.5普通硅酸盐水泥。水:乌鲁木齐市自来水。细骨料:筛洗后的中砂,基本性能如表1所示。粗骨料:6~25 mm级配的卵石,基本性能如表2所示。聚丙烯纤维选用防渗抗裂纤维I型润强丝纤维,钢纤维选用哑铃型DJ-4号纤维,基本性能如表3所示。混凝土强度:C40,根据团队前期研究,SFRC中纤维体积率为0.8%,PFRC中纤维掺量为1.2 kg/m3,配合比如表4所示。

表1 砂的基本物理化学性能Table 1 Basic physical and chemical properties of sand
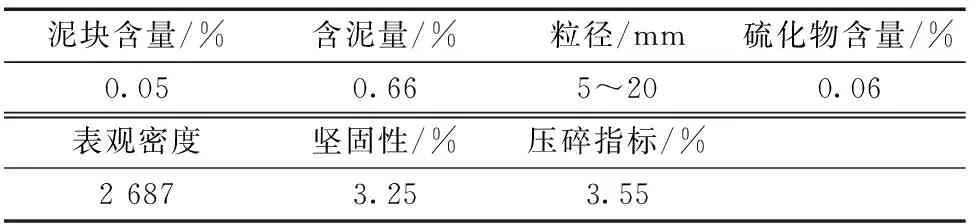
表2 卵石的基本物理化学性能Table 2 Basic physical and chemical properties of rocks

表3 纤维的基本物理性能Table 3 Basic physical properties of fibers

表4 混凝土配合比Table 4 Concrete mix ratio
1.2 试验方法
试验采用快速冻融法,依据《普通混凝土长期性能和耐久性能试验方法标准》(GB/T 50082—2009)[11],试验冻融循环时间设定在2~4 h内,融化时间大于冻融时间的1/4,冻结时的温度控制在(-18±2) ℃,融化时的温度控制在(5±2) ℃。
制作了两类不同尺寸的试块,其中的立方体试块用以测定冻融循环后的轴心抗压强度、劈裂抗拉强度,棱柱体试块用来测定动弹性模量,如表5所示。具体试验步骤如下。
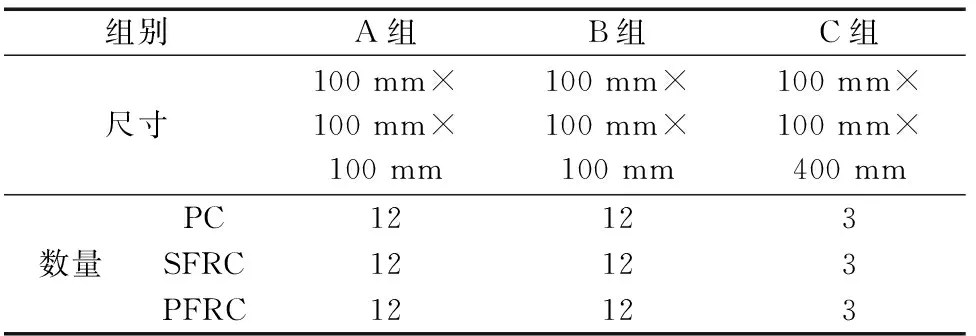
表5 混凝土试块的尺寸与数量Table 5 Size and quantity of concrete test blocks
(1)对所有试块进行标准养护,待养护结束后按试验类型分为A、B、C 3组,A组用于轴心抗压试验,B组用于劈裂抗拉试验,C组用于动弹性模量试验。
(2)除冻融循环0次的试块直接进行轴心抗压试验、劈裂抗拉试验、动弹性模量试验外,其余试块放入冻融循环试验机进行冻融循环试验。
(3)达到目标冻融循环次数后,取出相应试块进行试验,得到对应的轴心抗压强度、劈裂抗拉强度、动弹性模量。详细试验如图1所示。

图1 实际试验图Fig.1 Actual test chart
2 试验结果与分析
2.1 强度劣化分析
图2所示为PC、SFRC、PFRC抗压强度损伤率与冻融循环次数之间的关系,其抗压强度损失率为
(1)
式(1)中:Fc0为未经冻融循环时PC、SFRC、PFRC的抗压强度;Fc(N)为N次冻融循环后PC、SFRC、PFRC的抗压强度。
图3所示为PC、SFRC、PFRC抗拉强度损伤率与冻融循环次数的关系,其抗拉强度损失率为
(2)
式(2)中:Ft0为未经冻融循环时PC、SFRC、PFRC的抗拉强度;Ft(N)为N次冻融循环后PC、SFRC、PFRC的抗拉强度。
由图2、图3可知:冻融循环25次时,PFRC、SFRC、PC的抗压强度损失率分别为1.30%、15.32%、18.28%,抗拉强度损失率分别为13.90%、10.57%、11.72%;冻融循环75次时,PFRC、SFRC、PC的抗压强度损失率上升至10.22%、20.99%、38.94%,抗拉强度损失率上升至21.35%、52.27%、59.14%。在整个过程中,PFRC、SFRC、PC的强度损失率和循环次数正相关,纤维混凝土的抗压强度损失率明显低于普通混凝土,而且纤维混凝土的抗压强度损失率和抗拉强度损失率都小于PC,这是因为混凝土内部微裂缝的应力集中现象是导致混凝土开裂的主要原因,而纤维的掺入使其产生“纤维桥联”现象,减缓混凝土微裂缝的发展和应力集中。此外,在整个冻融过程中SFRC的抗压强度损失率大于PFRC,这是由于聚丙烯纤维的直径是钢纤维的11%,单位体积内纤维根数多、纤维间距小,而且钢纤维的弹性模量在冻融循环的温度限制内几乎不变,聚丙烯纤维的弹性模量随温度降低而提高,冻融循环时聚丙烯纤维弹性模量的变化有利于抵消冻胀力。

图2 冻融循环次数与抗压强度损伤率的关系Fig.2 Relationship bewteen the damage rate of compresssive strength and the number of freeze-thaw cycles

图3 冻融循环次数与抗拉强度损伤率的关系Fig.3 Relationship between the damage rate of tensile strength and the number of freeze-thaw cycles
2.2 冻融损伤分析
目前对于混凝土损伤有多种评价指标,聂彦峰等[12]将粗糙集理论(rough set theory,RST)运用到混凝土耐久性评价指标评价上,计算超声波波速、长度变化率、回弹值、侵蚀深度、质量变化率5个评价指标的权重得到动弹性模量的权重系数最大。乔宏霞等[13]使用Copula函数对混凝土剩余寿命进行预测,选取了超声波声速和质量损失率作为评价指标,通过建立退化模型并进行分析得到超声声速(动弹性模量)比质量损失更适合作为混凝土损失的评价指标。选用动弹性模量作为损伤的评价指标,结合损伤力学,定义冻融损伤度为
(3)
式(3)中:E0为初始时PC、SFRC、PFRC的动弹性模量;E(N)为冻融循环N次后PC、SFRC、PFRC的动弹性模量;En为相对动弹性模量。
图4所示为PFRC、SFRC、PC损伤度和循环次数之间的关系,由图4可知,冻融循环初期SFRC和PC的损伤度差距较小,经过50次冻融循环后,SFRC的冻融损伤度明显低于PC。而PFRC的抗冻融损伤能力从始至终均优于PC、SFRC。原因在于:混凝土的冻融损伤与其内部毛细孔内自由水有关,无论是自由水在冰点时体积膨胀导致毛细孔孔壁破裂甚至产生新的裂缝还是产生浓度差导致混凝土内部空隙间形成渗透压,都会使混凝土内部的裂缝在冻融过程中不断产生、发展[14-15]。钢纤维的掺入使得钢纤维表面的凹凸界面和基体紧密咬合,导致内部裂缝难以扩展,从而增强抗冻能力。聚丙烯纤维的掺入使内部气孔数量增多,密实度下降,有助于提高抗冻性能,减缓微裂缝发展[16-17]。
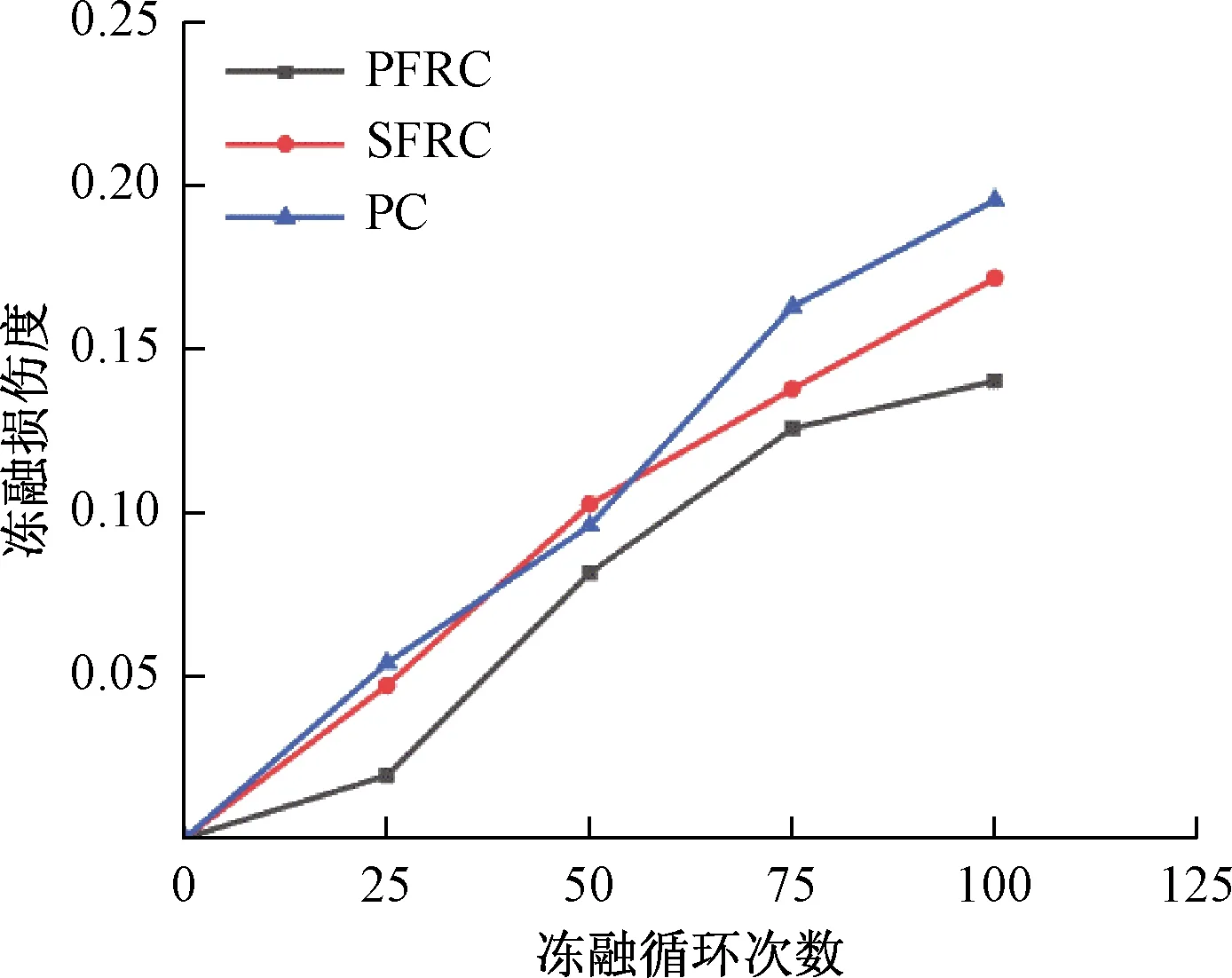
图4 冻融循环次数和冻融损伤度的关系Fig.4 Relationship between freeze-thaw damage degree and freeze-thaw cycle number of concrete
3 冻融循环下纤维混凝土损伤模型
3.1 基于Weibull分布的纤维混凝土损伤模型
目前描述混凝土冻融损伤的模型主要分为两种,一种是形如式(4)的指数函数,另一种是形如式(5)的二次函数。但这两类函数都存在不足:指数函数和二次函数都不符合在未冻融时,混凝土冻融损伤率为0的边界条件;二次函数依靠试验数据的统计思想,得到基于试验的经验公式,用这种公式来描述混凝土的内部的随机损伤不够严谨。在混凝土结构的寿命预测中,根据确定性模型预测得到的服役寿命具有一定模糊性,所以有必要通过使用概率法准确预测混凝土的服役寿命[18]。
D(N)=1-aebN
(4)
式(4)中:a、b为材料系数。
D(N)=a1N2+b1Ν+c
(5)
式(5)中:a1、b1、c为材料系数。
Weibull分布是一种基于链条模型并结合统计学和概率论的破坏理论,常用来反映材料失效的概率分布,其寿命预测功能在各个领域被广泛应用。当冻融循环下纤维混凝土疲劳失效服从Weibull分布时,将冻融损伤度和分布函数等价,表达式为

(6)
式(6)中:α为特征疲劳参数;β为形状参数;α>0,β>0。
概率密度函数f(N)为
(7)
式(7)中:若β=1时,f(N)可看作指数密度函数;若β=3~4时,f(N)可看作正态分布密度函数。
3.2 参数的确定
因为式(6)为无法直接拟合的非多项式函数,故需采取对式(6)取两次对数达到线性化,即
(8)
由于式(8)是形如Y=AX+B的线性形式,利用数理统计中的线性拟合、极大似然估计来得到特征参数α和β的值,图5所示为特征参数相关性。

图5 特征参数相关性Fig.5 Characteristic parameter correlation
PC、SFRC、PFRC的Weibull分布函数特征参数估计结果如表6所示。结合表6和式(6)计算PFRC、SFRC、PC的冻融损伤度,试验值与计算值如表7所示。试验值与计算值比值的方差为0.12,变异系数为0.12,吻合良好。

表6 Weibull分布特征参数Table 6 Weibull distribution characteristic parameters

表7 冻融损伤度计算值与试验值Table 7 The comparison between the calculated value of freeze-thaw damage and the test value
将表6中特征参数代入式(6),建立基于Weibull分布特征参数的冻融损伤演化图,如图6所示。
由图6可知,冻融循环前期PFRC表现出优于PC、SFRC的抗冻性,但PFRC的冻融损伤曲线上升斜率也明显高于PC、SFRC,导致PFRC后期冻融损伤度高于PC、SFRC,SFRC在整个冻融循环过程中的冻融损伤度均小于相同循环次数下的PC。

图6 冻融损伤演化Fig.6 Evolution of freeze-thaw damage
3.3 力学性能衰减模型
随着冻融循环次数增加,PFRC、SFRC、PC的强度损失率呈正比增加,即单位循环次数内强度损失率为定值,令N次循环后混凝土强度函数为可微函数F(N),定义F0为循环0次时混凝土强度,k为强度损失率且大于0,则N次到(N+ΔN)时强度损失率为
(9)
变换得:
(10)
对式(10)微分方程积分得:
(11)


表8 强度损失率Table 8 Strength loss rate
3.4 冻融损伤度与相对抗压、抗拉强度演化方程
将式(11)恒等变形得:
(12)
联立式(6)、式(12)得冻融损伤度由相对强度表达的演化方程:
(13)
联立式(13)、式(3),得:
(14)
由表9、表7可知,强度衰减率、冻融损伤率与冻融循环次数的相关性良好,联立消去循环次数N得式(13)。由式(13)可知,冻融循环下SFRC、PFRC、PC冻融损伤度和相对剩余抗压、抗拉强度关系符合指数函数和以e为底的对数函数的复合形式,考虑到冻融损伤度和相对剩余强度并不完全符合正比例函数,将表6、表8的结果代入式(13)、式(14),可以实现冻融循环下PFRC、SFRC、PC的相对抗压强度衰减率、相对抗拉强度衰减率与损伤度、相对动弹性模量的换算。
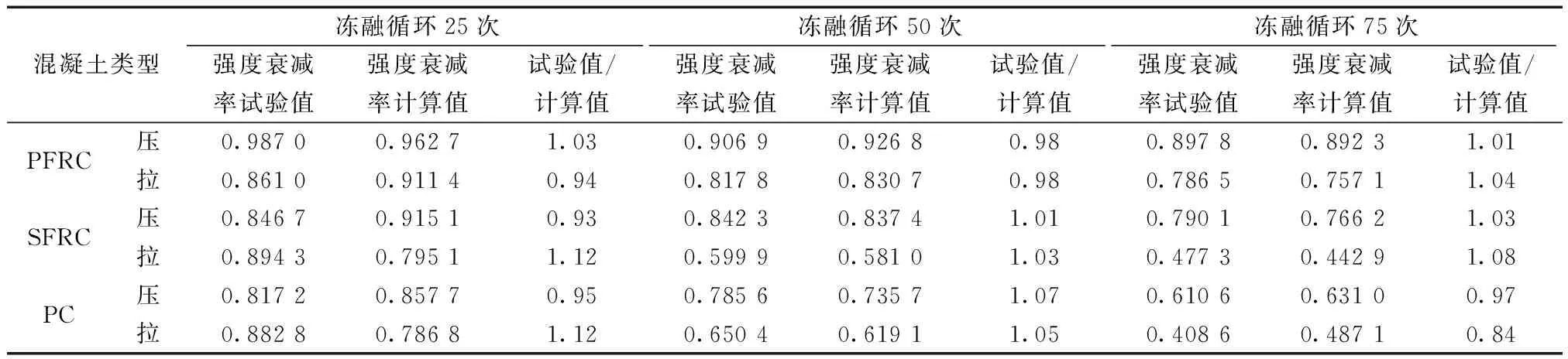
表9 强度衰减率计算值与试验值Table 9 The calculated value of intensity attenuation rate is compared with the experimental value
4 结论
(1)冻融初期SFRC和PC的损伤度相差不大,在循环50次后,PC的损伤度大于SFRC,而PFRC从冻融循环开始到结束时,损伤度都小于SFRC、PC。PFRC、SFRC、PC的抗压强度衰减率、抗拉强度衰减率和循环次数呈正相关,大小关系为PC>SFRC>PFRC。
(2)基于Weibull分布建立SFRC、PFRC、PC的冻融损伤模型,计算值与试验值吻合较好,可为冻融地区纤维混凝土劣化损伤提供一定的理论参考。
(3)利用Weibull分布建立的冻融损伤模型和力学性能衰减模型联立推导得出SFRC、PFRC、PC的冻融损伤度和相对抗压强度、相对抗拉强度之间的关系式,可以实现冻融循环下PFRC、SFRC、PC相对抗压强度衰减率、相对抗拉强度衰减率与冻融损伤度、相对动弹性模量的换算。

