车载综合电力系统关键参数对系统稳定性的影响

高强，廖自力，袁东，刘春光

(陆军装甲兵学院 兵器与控制系，北京 100072)

0 引言

与传统履带式装甲车相比，轮式电传动装甲车具有更优越的机动性、灵活性，特别是在静音行驶模式下还具备低噪声、高隐蔽的特点，逐渐成为当代战斗车辆的主流发展方向[1-2]。车载综合电力系统作为轮式电传动装甲车的核心系统近年来取得了较快发展，目前已经实现了“发电- 配电- 负载”一体化[3-4]。

车载综合电力系统不同于传统大电网或者小型电站输配电系统以及舰载电力系统，主要表现在：1)系统只能工作于离网(孤岛)模式，且系统体积、器件容量严重受限，导该系统呈现弱惯性；2)采用直流微网的结构，变流器种类数量多，非线性强，变流器的性能会对系统电压、电流产生重要影响[5]；3)车辆具有静音行驶、爬坡、加速、越野、高速等多种复杂工况，需求功率动态变化，对系统应变能力要求高。

因此，车载电力系统极易出现运行时突然崩溃、存在瞬态过大破坏性脉冲、母线电压低频振荡、电源噪声大、局部模块过热等稳定性问题，使得系统瞬态性能下降，能量转换效率低，严重的可能直接导致系统失效，造成灾难性后果[6]。尤其是近些年来装甲车辆电子信息化的发展，车载通信网络、瞄准测距等精密仪器越来越多，对车载电力系统稳定性要求也越来越高，母线电压失稳可能会导致无法正常工作，甚至会损坏设备，造成巨大损失。

当前主要从源载功率匹配、功率分频的角度进行系统设计。文献[7]针对电动汽车不同工况分别计算负载需求功率阈值，选取动力电池以提供足够的功率。文献[8]利用小波变换分离负载需求的功率高频与低频分量，实现了负载频率与动力源输出特性的匹配。以上方法都在一定程度上保证了系统的正常运行，并取得了较好的效果。但对于车载综合电力系统，要进一步提高复杂工况下系统的稳定性，必须确定导致系统失稳的关键参数以及影响规律，从而在设计上满足系统稳定性要求。

本文以某型8×8轮式装甲车车载综合电力系统为基础建立系统的小信号模型，并推导出各微源的输出阻抗与电机负载的输入阻抗。通过改进李安寿[9]提出的实轴禁区和扇形禁区判据，并结合幅值裕量与相位裕量需求，得到车载综合电力系统小信号稳定判据。通过波特图直观展示了超级电容、DC/DC滤波电感、支撑电容、驱动电机转速与转矩等关键参数对系统稳定性的影响规律。最后通过仿真实验验证了该稳定判据的有效性，同时对系统关键参数的优化选取提出了合理化意见。

1 车载综合电力系统建模

某型8×8轮式电传动装甲车车载综合电力系统拓扑结构如图1所示，本文主要研究车辆在静音行驶模式下的系统稳定性问题。车辆工作在静音行驶模式下采用8×8模式驱动即8个轮毂电机同时工作，为了研究方便，认为车辆平稳行驶时载荷平均。此时发动机- 发电机组停止工作，系统由动力电池与超级电容供电，负载主要为8个轮毂电机，拓扑结构如图1中虚线框内所示。

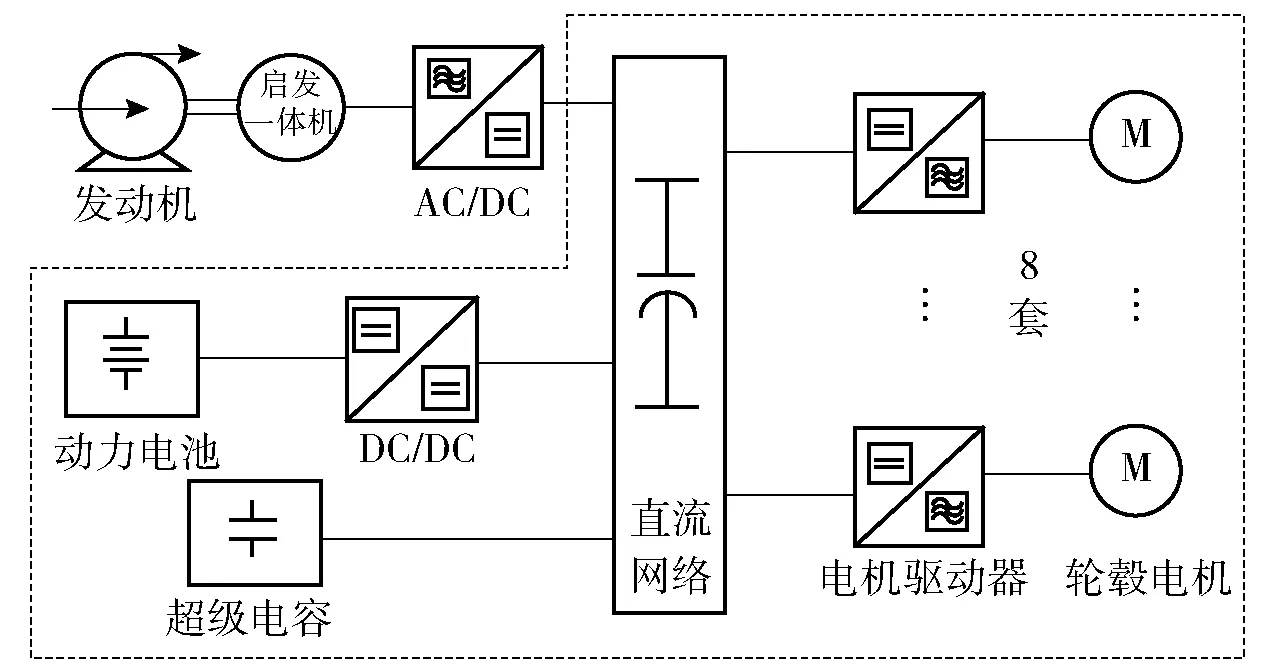
图1 静音行驶时车载电力系统拓扑结构Fig.1 Topology of vehicular integrated power system in engine-off operation mode

结合静音模式下的系统拓扑结构，为方便后文分析，首先对各微源、负载变换器进行小信号建模，得到各模块输入/输出阻抗。

1.1 DC/DC变换器小信号建模

车辆在静音行驶模式下DC/DC变流器工作在Boost模式，此时DC/DC变换器非理想状态下的电路拓扑结构[10]如图2所示。图2中，L、rL分别为变流器电感及等效内阻；T、rT分别为二极管及二极管内阻；Cs、rCs为支撑电容与电容内阻；G为绝缘栅双极型晶体管，rG为开关管内阻；ubat为动力电池电压；ubus为母线电压；iL为电感电流；ibus为变流器输出电流。

DC/DC变流器采用母线电压外环和电感电流双闭环控制策略，控制框图如图3所示。图3中，GiPI、GuPI分别为电流环和电压环PI控制器传递函数，Gm为脉宽调制调制器(PWM)传递函数，Zo为开环输出阻抗；Gii为电流传递函数；Giu为开环输入导纳；Gid为控制到输入传递函数；Guu为开环输入到输出传递函数；Gud为控制到输出传递函数；ubusref为标称母线电压。

由此得到DC/DC变流器闭环输出阻抗为

(1)

式中：

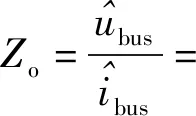
(2)

D为稳态时开关管占空比，s为频域，表示信号·对应平衡状态的扰动量；

(3)

(4)

(5)

IL为稳态电感电流，Ubus为稳态电压；

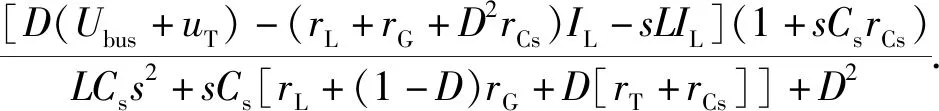
(6)

1.2 超级电容小信号建模

超级电容电路拓扑结构[11]如图4所示。图4中，Rs为串联电阻，Rp为并联电阻，uC为电容电压，uo为输出电压，i为电容电流。

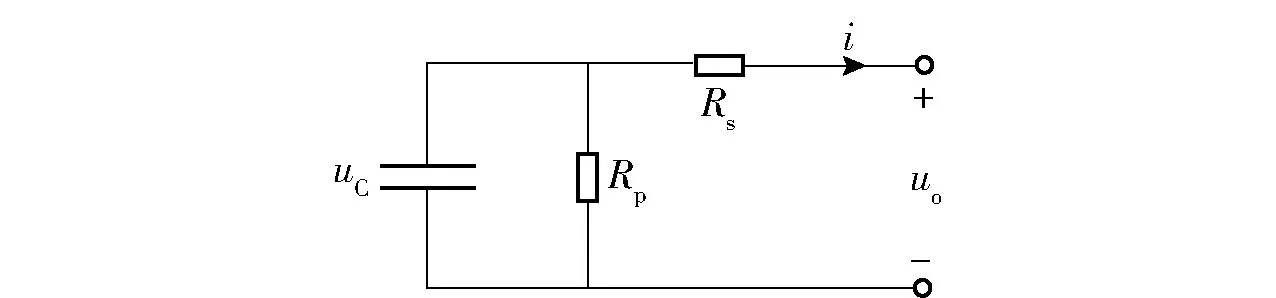
图4 超级电容电路拓扑结构Fig.4 Topology of super-capacitor

超级电容状态方程为

(7)

(7)式转化到频域，可得到线性化小信号模型，从而得到超级电容输出阻抗为

(8)

1.3 电机驱动器—轮毂电机系统小信号模型

轮毂电机采用永磁同步电机，为方便进行小信号分析，假设电机采用电机d轴定子电流id=0 A控制，则电机驱动器- 永磁电机结构[12-13]如图5所示。图5中，ia、ib、ic为三相电流，iq为电机q轴定子电流，ω为电机转速，ωref为参考转速。

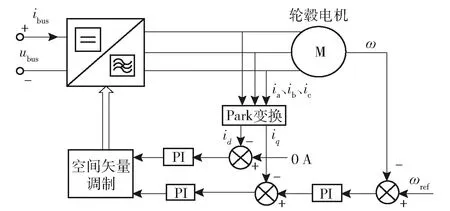
图5 电机驱动器- 永磁电机结构Fig.5 Structure of motor controller and permanent magnet motor

在不考虑驱动器功率损耗以及电机热损耗时，驱动器输入端功率与电机输出功率相等，即

ubusibus=Tω，

(9)

式中：T为电机转矩。

在(ibus,ubus,T,ω)的稳态工作点(Ibus,Ubus,Tm,ωm)附近加入扰动，去掉高阶项，可得到小信号模型：

(10)

(11)

电机驱动器——永磁同步电机系统小信号框图如图6所示。图6中，Gi、Gv分别为电流环和电压环控制器传递函数，Vm为载波幅值，K为比例系数，P为电机极对数，R为电机内阻，J为转动惯量，φf为反电势。

图6 电机驱动器—永磁同步电机系统小信号框图Fig.6 Block diagram of small signal of motor controller and permanent magnet motor

从而求得母线电压到转速的传递函数为

(12)

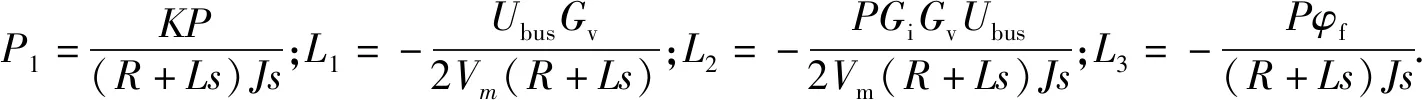
结合(11)式，进而求得电机驱动器——永磁同步电机负载系统输入导纳为

(13)

2 车载综合电力系统小信号稳定判据

在小信号稳定性分析方法中，阻抗法最流行，也最易应用于工程上[14]。但是基于阻抗法分析分布式电源系统的稳定判据，例如幅值相位增益判据(GMPM)、电源分析综合判据(ESAC)、最大峰值判据(MPC)等，都存在一定的保守性。李安寿[9]提出的实轴禁区和扇形禁区判别法从理论上消除了系统稳定裕度的保守性，但是他只给出了在已知源的输出阻抗情况下负载输入阻抗阻抗设计原则，对于车载综合电力系统，常常需要分析在特定工况下即负载输入阻抗确定的情况下源的输出阻抗变化对系统稳定性的影响，因此本文在前人基础上拓展设计了适合车载综合电力系统的阻抗设计规则。结合本系统拓扑结构以及6 dB的幅值裕量与30°的相角裕量需求，给出禁区范围在极坐标和波特图上的表示如图7所示。图7中，Zin为输入阻抗，Zout为输出阻抗，γ表示相角裕量，A表示幅值裕量。

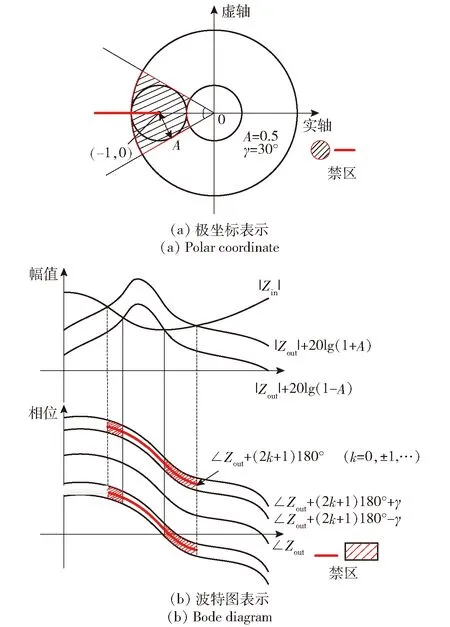
图7 满足6 dB的幅值裕量与30°的相角裕量禁区Fig.7 Forbidden zone of 6 dB gain margin and 30° phase margin

由此，车载综合电力系统阻抗设计规则描述为以下两种情况。

1) 已知系统前级输出阻抗、设计后级输入阻抗。

在|Zin|>|Zout|+20lg(1+A)的频率段，∠Zin无要求；

在|Zin|<|Zout|+20lg(1-A)的频率段，∠Zin不能穿过∠Zout+(2k+1)180°(k=0,±1,…)；

在|Zout|+20lg(1-A)<|Zin|<|Zout|+20lg(1+A)的频率段，∠Zin不能穿过由∠Zout+(2k+1)180°±γ围成的相位禁区。

2)已知系统后级输入阻抗、设计前级输出阻抗。

在|Zout|<|Zin|-20lg(1+A)的频率段，∠Zout无要求；

在|Zout|>|Zin|-20lg(1-A)的频率段，∠Zout不能穿过∠Zin+(2k+1)180°(k=0,±1,…)；在|Zin|-20lg(1+A)<|Zout|<|Zin|-20lg(1-A)的频率段，∠Zout不能穿过由∠Zin+(2k+1)180°±γ围成的相位禁区。

根据文献[15]给出的多源多负载级联系统阻抗比判据，并结合本系统拓扑结构(见图1)，得到车载综合电力系统小信号稳定判据描述如下：

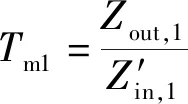
Zout，1、Zout，2分别为动力电池-DC/DC与超级电容的输出阻抗，Zin,j为第j组电机驱动器——轮毂电机负载的输入阻抗。

3 关键参数对系统稳定性的影响

本文研究对象为某型8×8轮式装甲车车载综合电力系统，其参数如表1所示。由于车内空间有限，超级电容阵列容量不能太大，而超级电容对母线电压稳定具有重要影响；变流器的性能尤其是滤波电感、支撑电容会严重影响母线电压、电流质量；路面、工况复杂反映在电力系统上，即为轮毂电机转矩、转速的变化。因此根据车载综合电力系统自身特点，本文重点研究车辆在静音模式下超级电容、DC/DC滤波电感、直流侧电容、驱动电机转矩、转速5个参数对系统稳定性的影响。

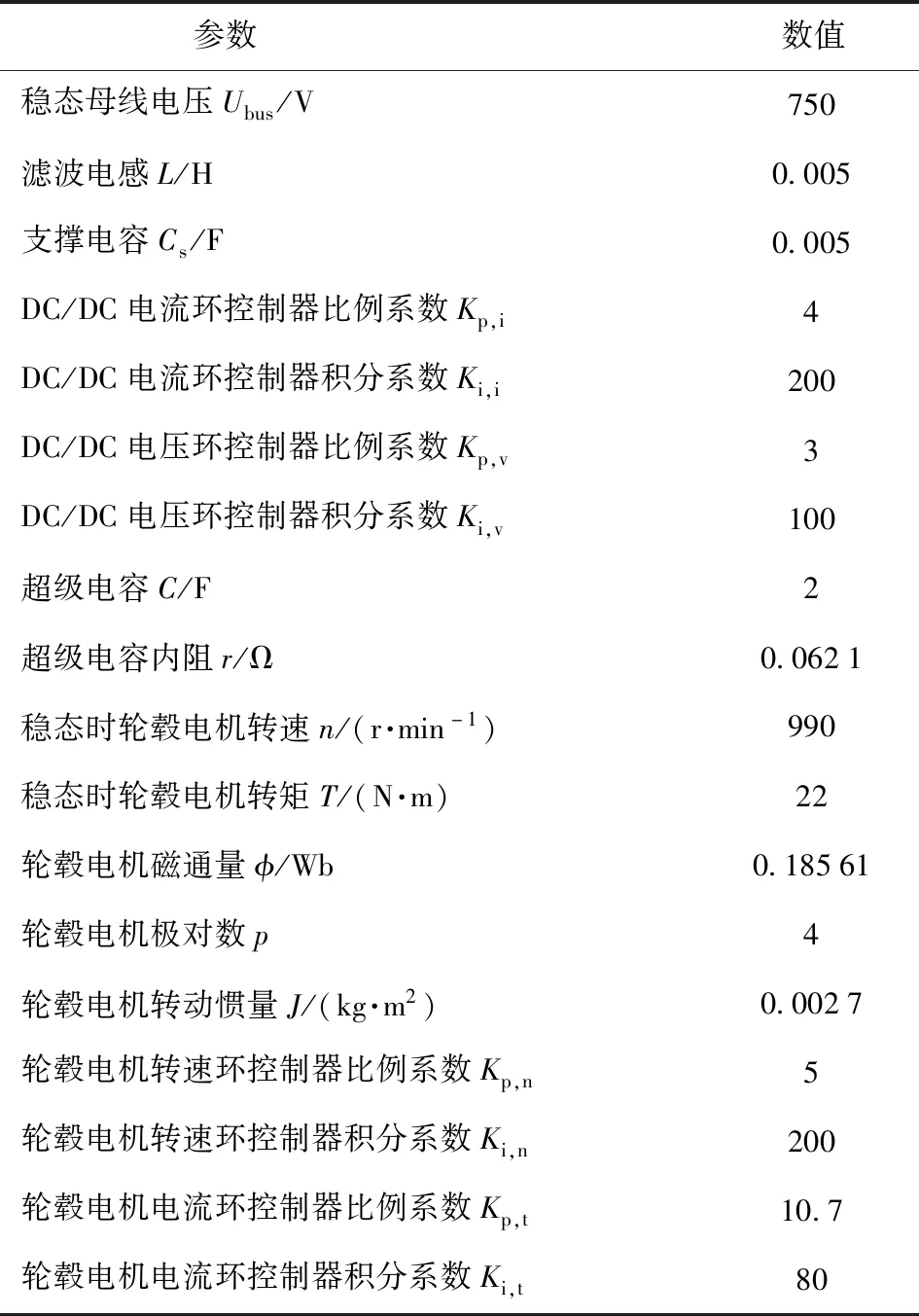
表1 某型8×8轮式车辆车载综合电力系统参数Tab.1 Parameters of vehicular integrated power system of a 8×8 wheeled armored vehicle

超级电容C对系统的影响如图8所示。图8中，超级电容C为唯一变量，由1 F逐渐增大到7 F，步长为1，其他参数保持不变。从图8(a)、图8(b)中可以看出，随着C的增大，∠Z′in,1、∠Zout,2始终不会穿过相位禁区，系统一直保持稳定。需要说明的是：图8(a)中，随着C的增大，|Z′in,1|在低频段变大，拓宽了系统稳定的频率范围；图8(b)中，随着C的增大，|Zout,2|在低频段逐渐减小，同样拓宽了系统低频段稳定范围。由此表明单从稳定性的角度考虑，超级电容越大系统稳定频段越宽，但效果并不明显。

图8 超级电容C对系统的影响Fig.8 Influence of super-capacitor on system

DC/DC的滤波电感L对系统的影响如图9所示。

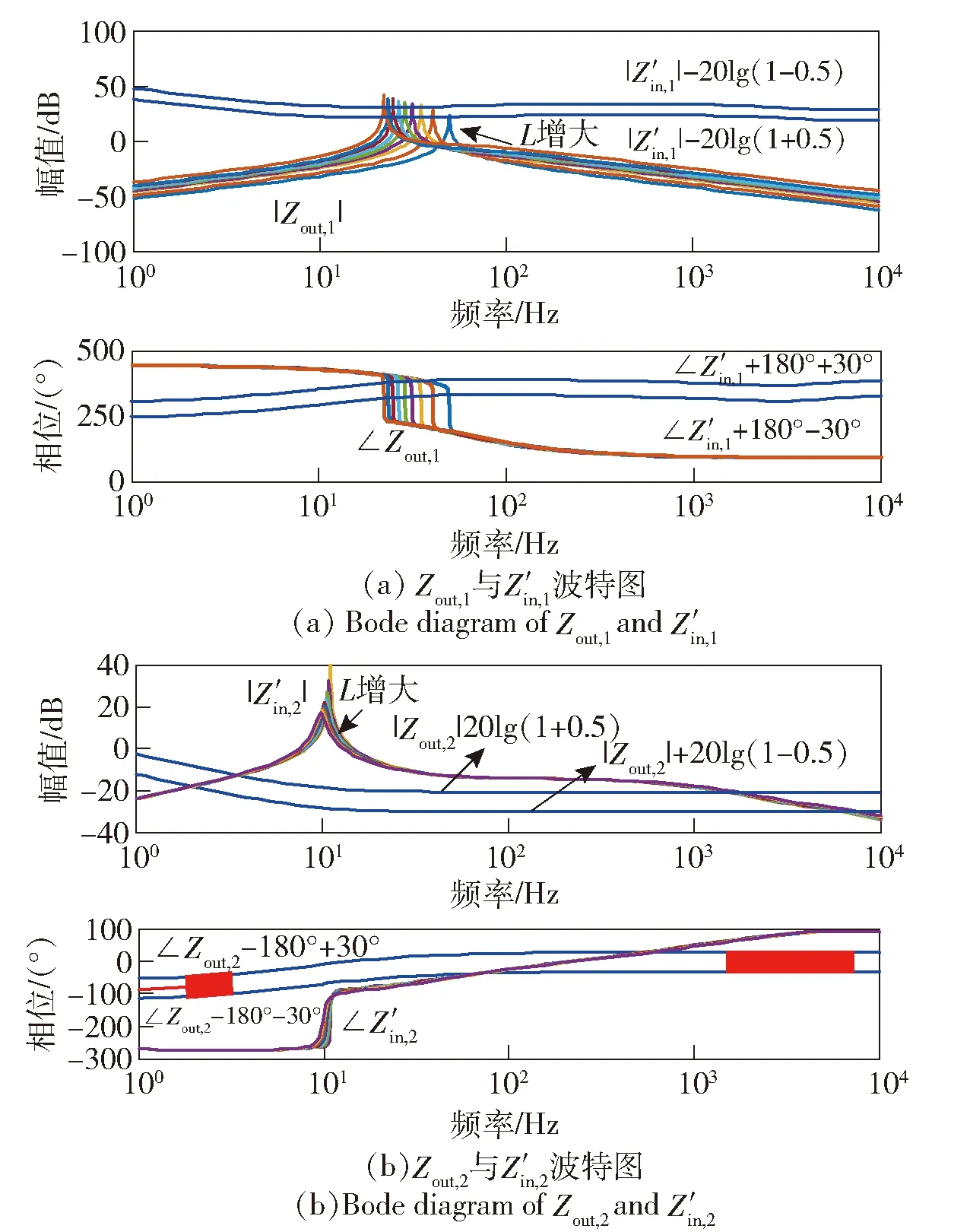
图9 DC/DC的滤波电感L对系统的影响Fig.9 Influence of DC/DC filter inductor on system

图9中，DC/DC滤波电感L为唯一变量，由0.004 H逐渐增大到0.012 H，步长为0.001 H，其他参数保持不变。图9(a)中，当L增大至0.007 H时，|Zout,1|进入(|Z′in|-20lg1.5，|Z′in|-20lg0.5)，此时∠Zout,1必然穿过∠Z′in,1+180°±30°的相位禁区，因此系统可能失稳。图9(b)中，随着L的增大，∠Z′in,2不会穿过相位禁区，因此Tm，2会保持稳定。由此可见，其他参数保持不变时，L增大会导致系统稳定性变差，保持系统稳定的最大L为0.006 H.

DC/DC的支撑电容Cs对系统的影响如图10所示。图10中DC/DC支撑电容为唯一变量，由0.001 F逐渐增大到0.009 F，步长为0.001，其他参数保持不变。图10(a)中，随着Cs的增大，|Zout，1|逐渐远离|Z′in|-20lg1.5，|Z′in|-20lg0.5)区域，在0.001～0.005 F之间，∠Zout,1必然穿过∠Z′in,1+180°±30°的相位禁区，因此系统可能失稳；在C′s大于0.005 F后，|Zout,1|<|Z′in,1|-20lg(1+0.5)，对∠Zout,1无要求，系统稳定。图10(b)中，随着Cs的增大，∠Z′in,2不会穿过相位禁区，因此Tm2保持稳定。由此表明其他参数保持不变时，Cs越大系统稳定性越好，保持系统稳定的最小Cs为0.005 F.

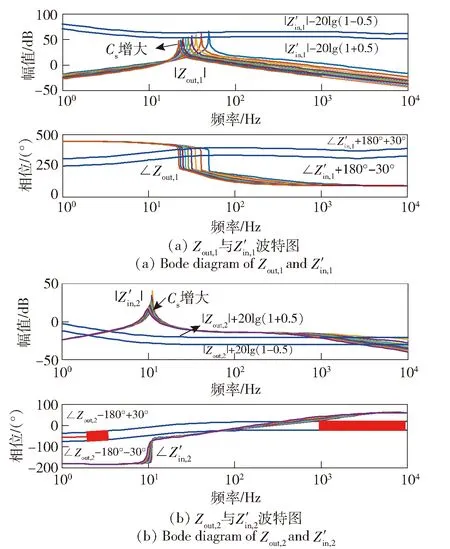
图10 DC/DC的支撑电容Cs对系统的影响Fig.10 Influence of DC/DC dc-link capacitor on system

轮毂电机转矩T对系统的影响如图11所示。图11中，轮毂电机转矩T为唯一变量，由20 N·m逐渐增大到200 N·m，步长为30，其他参数保持不变。图11(a)中，随着T的增大，|Z′in,1|在相同频率下幅值减小，相应的相位禁区逐渐增大，T增大到170 N·m时，∠Z′in,1穿过相位禁区，因此系统可能失稳。图11(b)中，随着T的增大，|Z′in,2|也在相同频率下幅值减小，相应的相位禁区也在逐渐变大，T增加到200 N·m时∠Z′in,2穿过相位禁区，此时可能导致系统失稳。因此，为了保证系统足够的稳定裕量，最大允许的T为170 N·m.

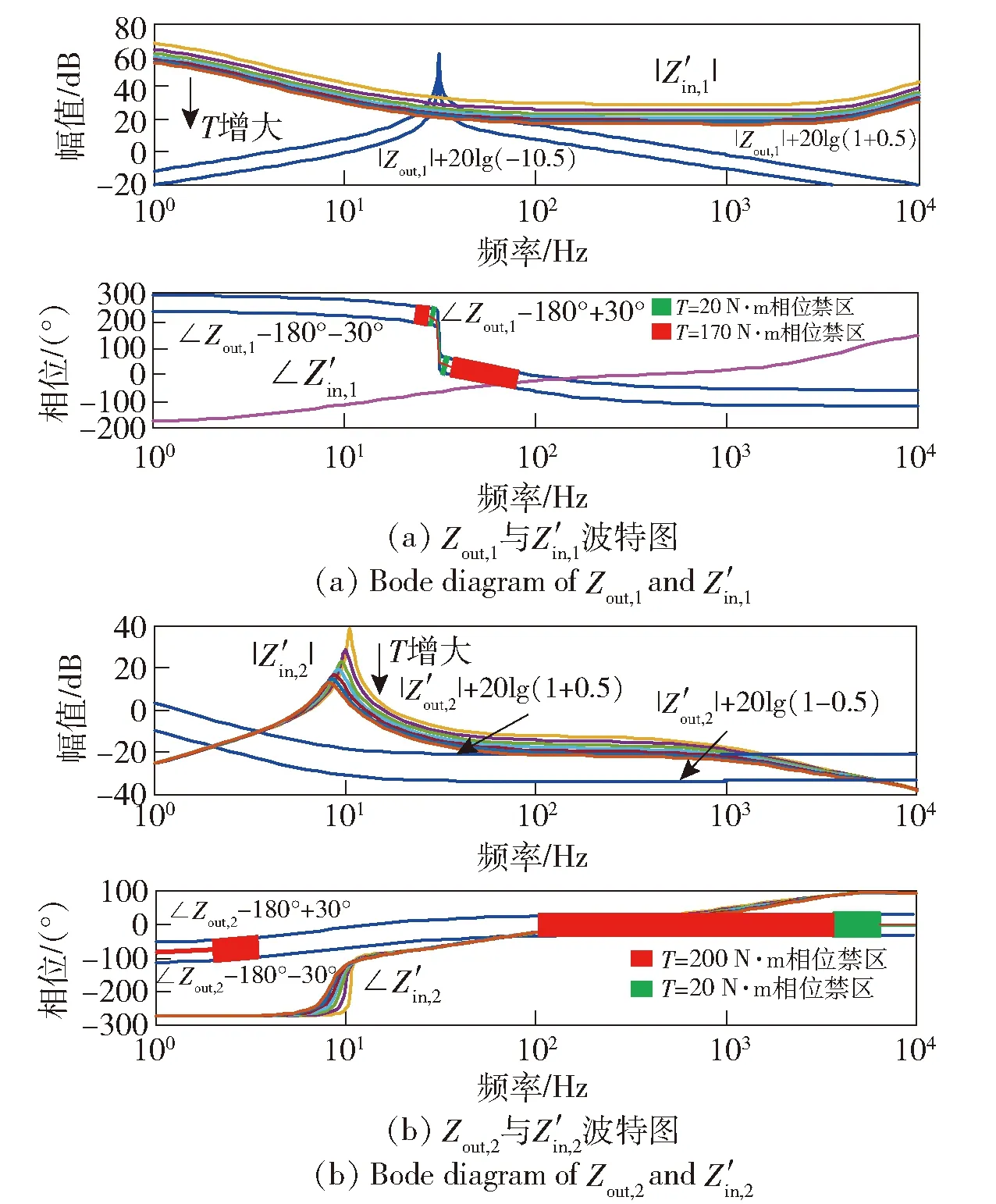
图11 轮毂电机转矩T对系统的影响Fig.11 Influence of hub motor torque on system

轮毂电机转速n对系统的影响如图12所示。

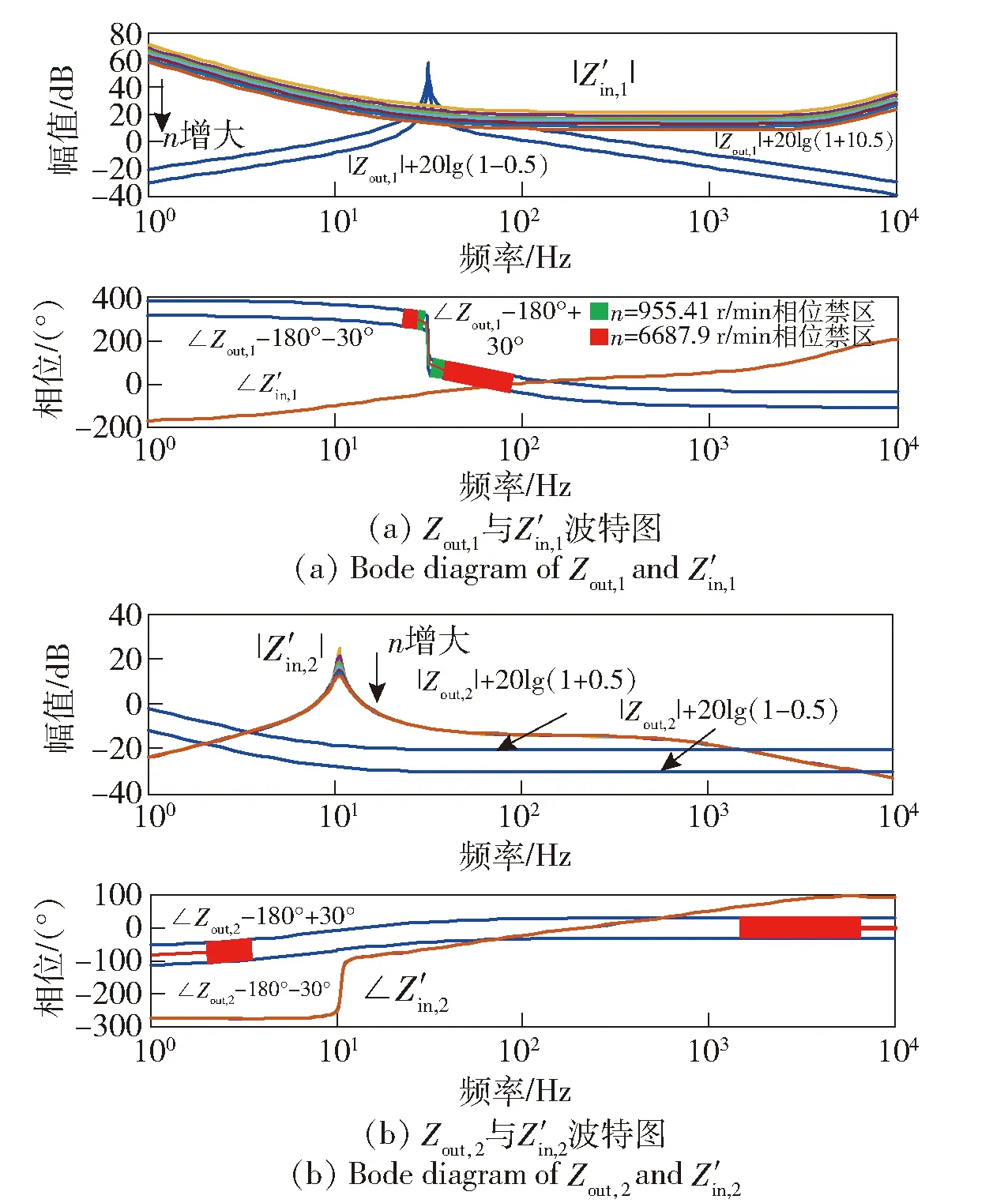
图12 轮毂电机转速n对系统的影响Fig.12 Influence of hub motor speed on system

图12中，轮毂电机转速n为唯一变量，由955.41 r/min逐渐增大到6 687.9 r/min，步长为955.41 r/min，其他参数保持不变。图12(a)中，随着n的增大，|Z′in,1|在相同频率下幅值减小，相应的相位禁区逐渐增大，n增大到6 687.9 r/min时，∠Z′in,1穿过相位禁区，因此Tm1可能失稳。图12(b)中，随着n的增大，|Z′in,2|也在相同频率下幅值减小，但效果不明显。相应的相位禁区也变化不大，∠Z′in,2一直未穿过相位禁区，表明Tm2保持稳定。由此可见，为了保证系统足够的稳定裕量，最大允许的n为6 687.9 r/min.

4 仿真验证

为验证第3节中车载综合电力系统的理论分析的正确性，根据表1中给定的参数，在MATLAB/Simulink软件环境下建立电池-DC/DC、超级电容、变频器- 轮毂电机仿真模型，得到参数变化时系统母线电压的仿真结果，见图13～图17.

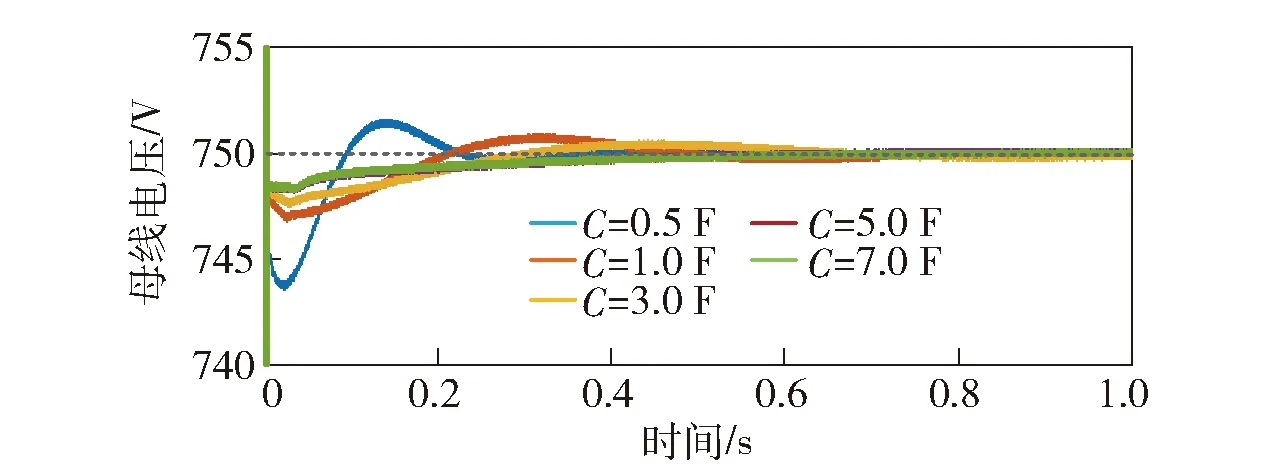
图13 超级电容C对母线电压的影响Fig.13 Influence of super-capacitor on bus voltage

图13所示为超级电容C分别为0.5 F、1.0 F、3.0 F、5.0 F、7.0 F时的母线电压波形。从图13中可以看出，随着超级电容的增大，母线电压波动变少，但超级电容继续增大效果则不明显。再者，随着超级电容的增大，母线电压达到稳态的时间增长，表明系统反应变慢。这一结论与阻抗判据分析的结果基本一致。

图14所示为DC/DC滤波电感值分别为0.006 H、0.008 H、0.010 H时母线电压波形。从图14中可见：当L为0.006 H时母线电压最终达到稳态750 V；当L为0.008 H时母线电压经过数次衰减振荡后达到稳态750 V；当L为0.010 H时母线电压最终在750 V上下波动，系统失稳。前文阻抗分析L最大为0.006 H，但是由于理论分析存在稳定裕量，当L为0.010 H时系统才会失稳。仿真结果与阻抗判据分析结果基本一致。

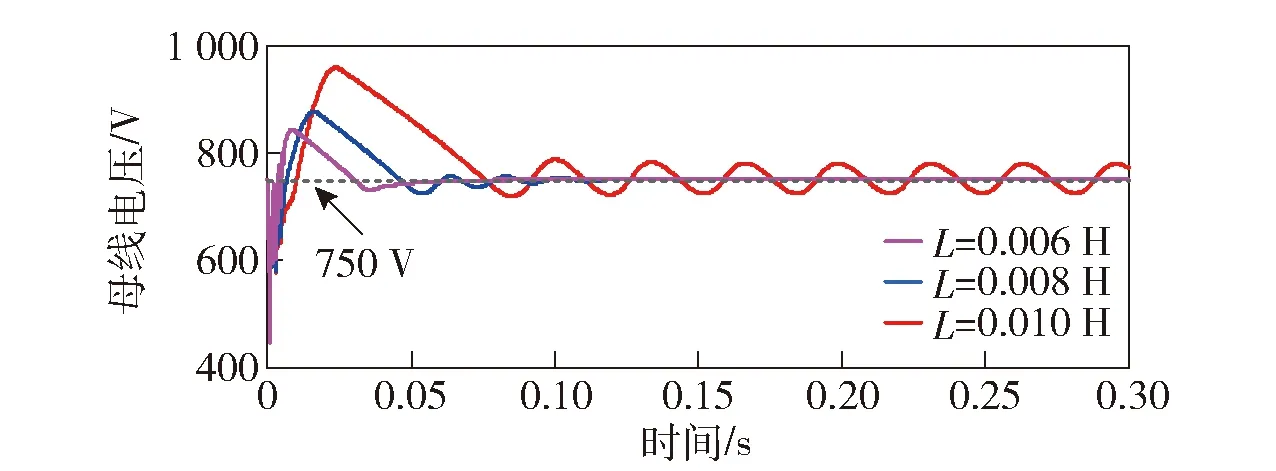
图14 DC/DC滤波电感L对母线电压的影响Fig.14 Influence of DC/DC filter inductor on bus voltage

图15所示为DC/DC支撑电容Cs分别为0.001 F、0.003 F、0.005 F时的母线电压波形。如图15所示：当Cs为0.005 F时的母线电压稳态值为750 V；当Cs为0.003 F时母线电压经几次衰减振荡后也能达到稳态750 V；当Cs继续减小时母线电压出现波动，并难以达到稳态750 V.情况与上述滤波电感L分析相似，由于理论分析存在稳定裕量，Cs理论分析值与仿真结果存在合理偏差。

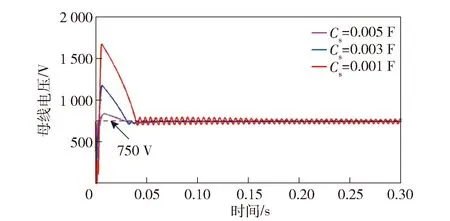
图15 DC/DC的支撑电容Cs对母线电压的影响Fig.15 Influence of DC/DC dc-link capacitor on bus voltage

图16所示为轮毂电机转矩分别为20 N·m、100 N·m、170 N·m、200 N·m时母线电压波形。从图16中可以看出，随着T的增大，母线电压在达到稳态的过程中振荡次数逐渐增多，系统稳定性下降。当T为170 N·m时母线电压经过多次振荡后最终能达到稳态750 V；当T为200 N·m时母线电压存在40 V左右的振荡，系统失稳。仿真结果基本与理论分析结果一致。

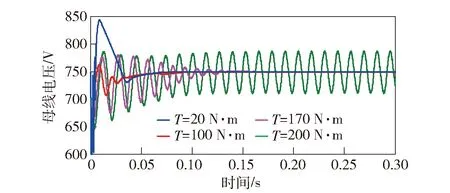
图16 轮毂电机转矩T对母线电压的影响Fig.16 Influence of hub motor torque on bus voltage

图17所示为轮毂电机转速n分别为4 777.05 r/min、5 732.46 r/min、6 687.90 r/min时母线电压波形。从图17中可以看出，随着n增大，母线电压达到稳态波动变大，当n为6 687.90 r/min时母线电压波动严重，已经不能回到稳态750 V，系统失稳。仿真结果与前文理论分析结果一致。

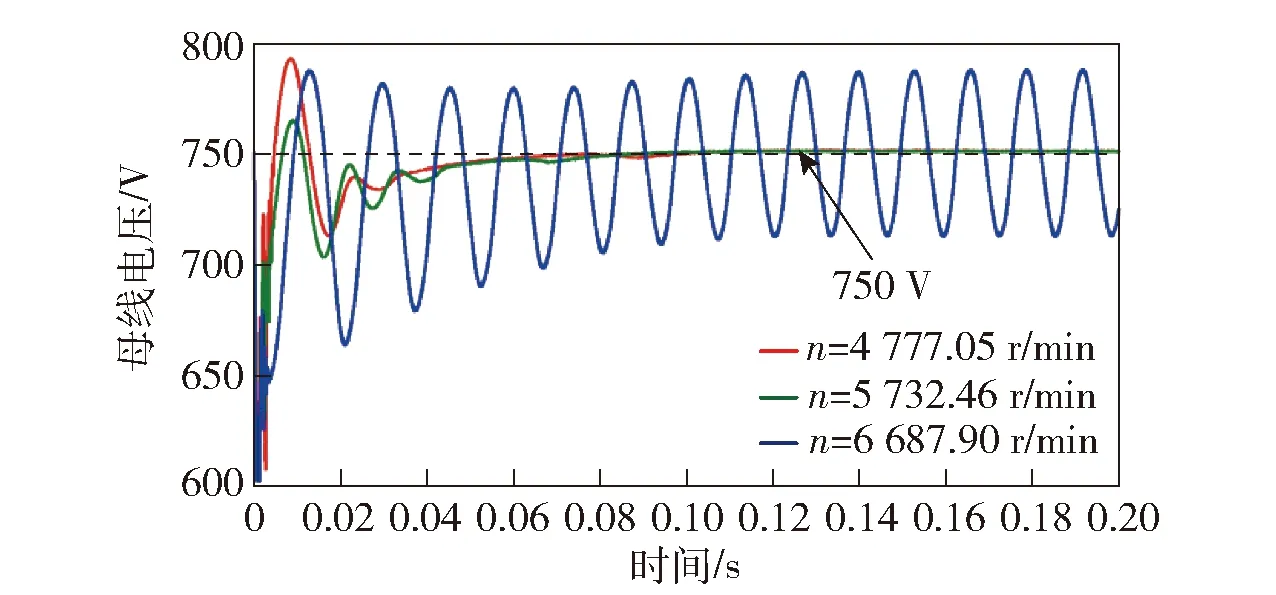
图17 轮毂电机转速n对母线电压的影响Fig.17 Influence of hub motor speed on bus voltage

5 结论

本文以某型8×8轮式电传动装甲车为研究基础，基于改进的阻抗比判据提出了车载综合电力系统小信号稳定判据，并通过波特图理论分析了静音行驶模式下系统的5个关键参数对稳定性的影响规律，最后通过仿真实验对理论分析结果进行了验证。得到主要结论如下：

1) 单从稳定性角度考虑，增大超级电容确实可以减少母线电压波动次数与幅值，但效果不是很明显，且超级电容主要影响系统在低频段的稳定性，对中高频段基本无影响，加之考虑该系统体积受限，超级电容容值可取2 F.

2) 在车辆静音模式下，该系统保持母线电压稳定的DC/DC滤波电感不得大于0.006 H，支撑电容不得小于0.005 F.

3) 静音行驶时，理想条件下能够保持系统稳定的轮毂电机转速最大为5 732.46 r/min；转速为990 r/min时，轮毂电机输出转矩最大为170 N·m.

4) 车载综合电力系统小信号稳定判据能够有效评估系统稳定性，有助于优化系统设计。