基于瞬态多物理场求解器的电磁轨道炮发射过程建模与仿真
林庆华,栗保明
(南京理工大学 瞬态物理国家重点实验室,江苏 南京 210094)
0 引言
电磁发射是近年比较活跃的一个前沿技术领域,电磁轨道炮、电磁线圈炮等研究方向受到广泛关注,并已经在一些关键技术上取得突破。发射过程的建模与数值仿真是支撑电磁炮技术发展的重要基础之一,它利用对发射过程物理图像及其规律的理论描述,为工程设计和试验提供参考。
大电流高速滑动电接触是电磁轨道炮发射工况的典型特征[1-2]。国内外为了研究高速滑动电接触及其所导致的电磁学、热学和力学效应,已经或正在开发一些专用计算程序,包括EMAP3D[3]、MEGA[4]、HERB[5]、EFEM3D[6]、RGUN3D[7]等。这些程序的核心功能是求解带有高速滑动电接触的电磁场问题,它们普遍采用了有限元方法,但在具体算法上有些差别,例如程序EMAP3D使用了节点元,程序EFEM3D使用的是棱边元。在电磁场计算的基础上,Hopkins等[8]将EMAP3D程序与著名的显式动力学计算程序DYNA3D耦合,用于求解电磁轨道炮在脉冲电磁力作用下的结构动态响应。Leyden等[9]将程序MEGA计算出的温度载荷传递给程序DYNA3D,实现了对电枢热软化过程的模拟。
电磁线圈炮中没有滑动电接触,其电磁场问题相对容易解决,然而一旦涉及到电枢在局域化感应涡流及电磁力作用下的发热和变形,以及电枢和导向管间的高速摩擦、碰撞,也会遇到与电磁轨道炮相似的非线性、多物理场耦合等问题。
以往的电磁炮建模与数值仿真以研究发射机理为主要目的,因此模型中只需考虑电枢- 轨道或者电枢- 线圈系统[10-11]。随着电磁炮技术的发展,数值仿真工作逐渐涉及到先进发射器结构和一体化发射单元(ILP)[12-14],特别是对于携带含能材料和电子部件的ILP,其发射安全性的研究和评估工作需要相关模型和数值仿真程序的支撑,这对电磁炮的建模和数值仿真提出了新的要求。
南京理工大学瞬态物理国家重点实验室开展电磁发射理论与技术研究已有十余年,逐步建立起涵盖电磁场、热场和结构场的瞬态多物理场模型,编写了电磁炮的求解器程序。本文简要介绍了该求解器的组成框架、基本功能、数学模型和计算方法,通过电磁轨道炮和电磁线圈炮的具体算例,展示了该求解器对电磁发射过程的仿真计算能力。
1 求解器框架与功能介绍
求解器的组成框架如图1所示。它针对的是包含脉冲电源、发射器和ILP在内的整个发射系统,具有电路、电磁场、热场、结构场4个功能模块,其中脉冲电源的放电过程用电路模型描述,发射器和ILP的工作过程用场模型描述。
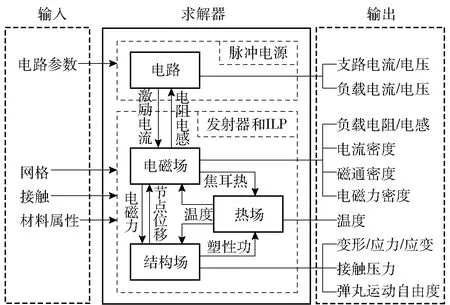
图1 求解器框架Fig.1 Framework of solver
电磁场是整个求解器的核心,它以脉冲电流作为激励条件,在求解域的导体内传导或感应出电流,产生焦耳热和电磁力的分布。激励电流可以通过数据曲线的形式直接输入,也可以通过场路耦合由电路模型实时计算。进行场路耦合计算时,发射器和ILP被视作电路的负载,每一时刻的负载电阻和电感参数可通过电磁场模型计算得到。
热场以电磁场产生的焦耳热和结构场的塑性功为热源,在导体内产生温升,并使热量在发射器和ILP内传导。热场的计算结果可以传递到电磁场和结构场,对电导率、力学本构关系等材料属性产生影响。
结构场以电磁场计算出的电磁力(洛伦兹力)为动力,在发射器和ILP内产生动力学响应,导致部件的变形、运动以及应力波在结构内的传播。结构场的运动和变形被回馈给电磁场,用于更新导体构型、计算电磁场的演化。为了描述发射过程中材料的力学行为,结构场中定义了如下5种材料模型:1)弹性模型;2)弹塑性模型;3)Johnson-Cook模型;4)正交各向异性弹性模型;5)弹塑性流体动力学模型。这些模型基本能够涵盖电磁炮所涉及的金属、非金属、纤维缠绕结构、含能装药等材料。
图1中的4个功能模块既可以同时耦合运行,也可以单独运行,或者选择其中几个组合运行,例如在刚体假设下可以不考虑结构场,只进行电磁、电路- 电磁耦合、电磁- 温度耦合等计算。
求解器的各物理场共用一套网格。输入量包括电路参数、有限元网格、接触、材料属性等,通过数据文件的形式读入。由于在求解器中已经完成输出量的计算和处理,输出的数据文件可以直接导入作图软件来绘制曲线图和云图。
2 数学模型与计算方法
2.1 电磁场
用运动坐标下的磁扩散方程和电流连续性方程来描述导体内的电磁场,满足
(1)
(2)
式中:A为矢量磁位;σ为电导率;μ为磁导率;φ为标量电位。当σ=0 S/m时,(1)式退化为Laplace方程,用于描述导体以外的绝缘体及自由空间。由(1)式和(2)式组成的电磁场方程组,可通过有限元- 边界元耦合方法求解[15]。
在电磁炮导电路径的某个截面上,施加具有一定波形的电流作为激励条件,或者采用场路耦合的方式,获得激励电流。以脉冲电容器组驱动下的轨道炮发射系统为例,电路模型如图2所示。图2中,电源采用多模块并联方式,每个模块k(k=1,2,…,n)中包含电容Ck、电感Lk、硅堆Dk、开关Kk,并计入杂散电阻Rk和RDk;轨道炮负载可视作可变电阻RL、可变电感LL以及电枢与轨道间接触电压Ua的串联,负载电流i流过轨道和电枢,并在炮尾轨道两端产生电压Ub,ik为各模块电流,R0为连接电源与轨道炮的输电线电阻,L0为电感。
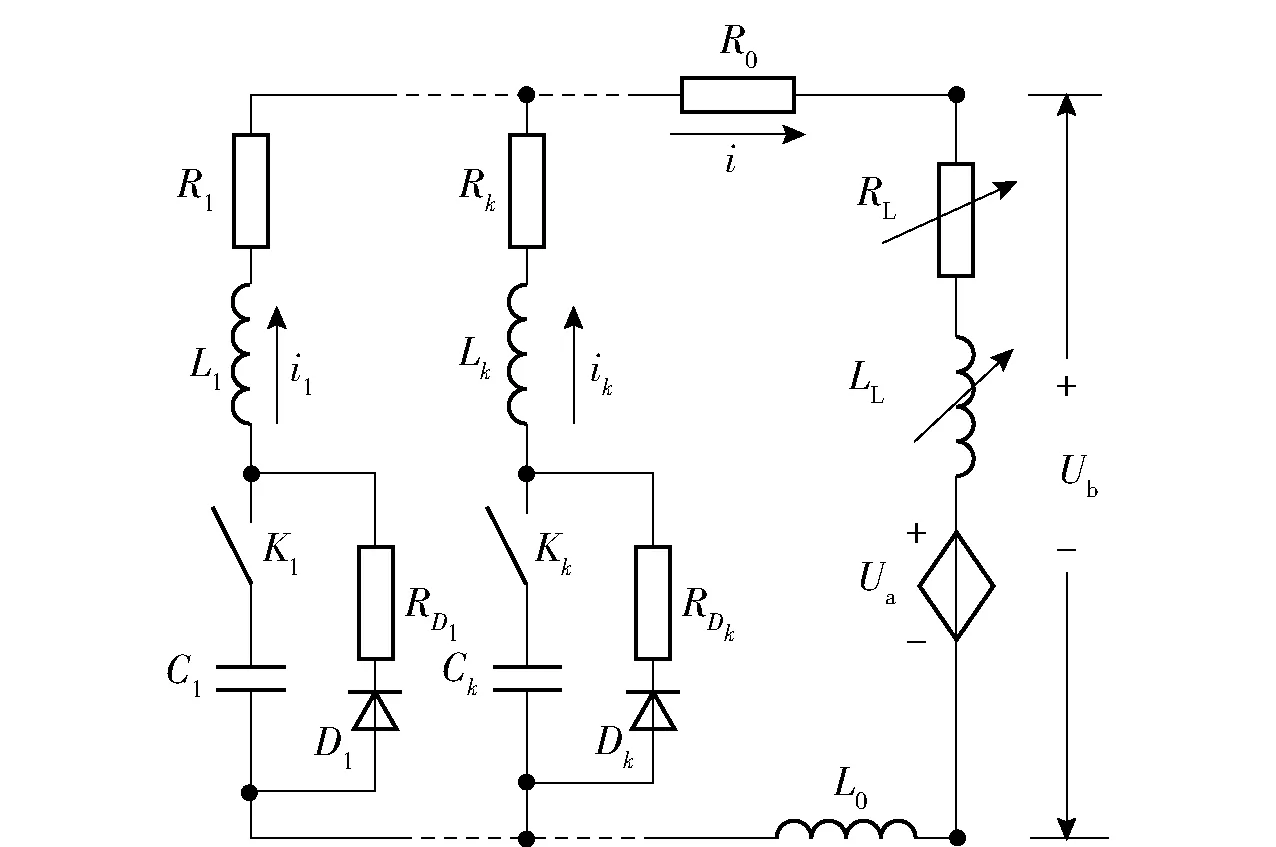
图2 发射系统的电路模型Fig.2 Circuit model of launching system
当模块的电容器电压uCk>0 V时,电路的数学模型如下:
(3)
当uCk<0 V时,电路的数学模型如下:
(4)
式中:
(5)
2.1.1 负载电阻
负载电阻和电感通过电磁场模型计算。通过电磁场可以计算出电流密度j,将其在导体区域VC内积分后,可以得到负载内的焦耳热功率为
(6)
式中:Ω为积分的体积微元。从电路的角度来看,焦耳热功率为
We=i2RL.
(7)
由于电磁场是由电流驱动的,在负载电流i已知的情况下,可以将负载电阻表示为
(8)
2.1.2 负载电感
磁场能量密度瞬时值wm与磁通密度B和磁场强度H有关,定义为
(9)
对于电磁炮这种不含高磁导率材料的磁路,将磁场能量密度在整个求解域V内积分,得到磁场储能为
(10)
由于磁场储能与负载电感的关系为
(11)
在已知负载电流i的情况下,可以根据磁场储能计算出负载电感为
(12)
在每个时间步,通过电磁场计算出负载电阻和负载电感,代入电路的常微分方程组,即(3)式~(5)式,然后用Ronge-Kutta方法求解出下一个时间步的负载电流。
2.2 热场
由于电枢是运动的,热场模型也被定义在运动坐标下,用傅里叶热传导方程描述为
(13)
式中:ρ为材料密度;c为材料比热;T为温度;kc为导热系数;t为时刻;Q为热源密度,来自于流过导体的电流所产生的焦耳热以及塑性变形产生的热量,
(14)
σs和ε分别为应力和应变,β为塑性功转化为热量的比例。热场模型的求解采用有限元法[16]。
2.3 结构场
由于电磁炮发射时产生很高的应力,ILP与内膛之间存在接触碰撞,而且发射周期只有短短的几毫秒,因此采用显式有限元方法[17]求解结构场。根据连续介质力学理论,结构场的控制方程组中包含质量守恒、动量守恒和能量守恒方程,满足
(15)
采用罚函数法处理发射器和ILP的各部件之间存在着的接触。检查每个从节点是否穿透主面,如果存在穿透,则在从节点和接触点之间施加界面力,其大小正比于穿透量,相当于在所有从节点和主表面之间布置一系列法向界面弹簧。另外,接触面的摩擦也利用等效弹塑性弹簧来实现。
3 电磁轨道炮发射过程的数值仿真研究
3.1 计算模型及参数
图3为计算模型的结构尺寸及有限元网格的示意图,模型中考虑了发射器及ILP的基本结构特征。图3(a)为发射器的截面,截面中心为ILP,D形轨道在其左右两侧相向布置,ILP上下两侧的矩形区域为绝缘体,发射器的外层为纤维缠绕层。图3(b)为ILP,由电枢、卡瓣、弹丸(内部装填炸药)组成。
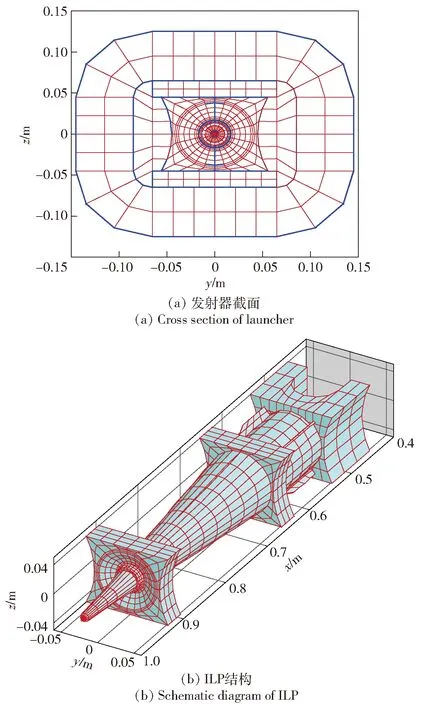
图3 模型网格与尺寸Fig.3 Mesh and size of the model
发射器长6.0 m,轨道表面之间的最短距离为90 mm.ILP整体质量约5.1 kg,其中弹丸质量3.1 kg,电枢、卡瓣等寄生质量为2.0 kg.在该算例中,轨道、绝缘体、卡瓣为弹性材料,电枢为弹塑性材料,发射器的缠绕结构为正交各向异性弹性材料(材料参数见文献[18]),装药为弹塑性流体动力材料(材料参数见文献[19])。
脉冲电源的总储能为60 MJ,由1 200个50 kJ储能单元组成,单元参数如表1所示。

表1 储能单元参数表Tab.1 Parameters of energy storage unit
储能单元分为20组,通过设置不同的开关触发延时进行时序放电,其中第1~4组在0 ms时刻触发,其他各组依次延时300 μs触发。
3.2 计算结果与讨论
3.2.1 脉冲电源放电过程
图4为脉冲电源的电流和电容器电压曲线。图4(b)为电容器两端的电压曲线,图中标注的数字与延时触发的第5~20组单元对应。
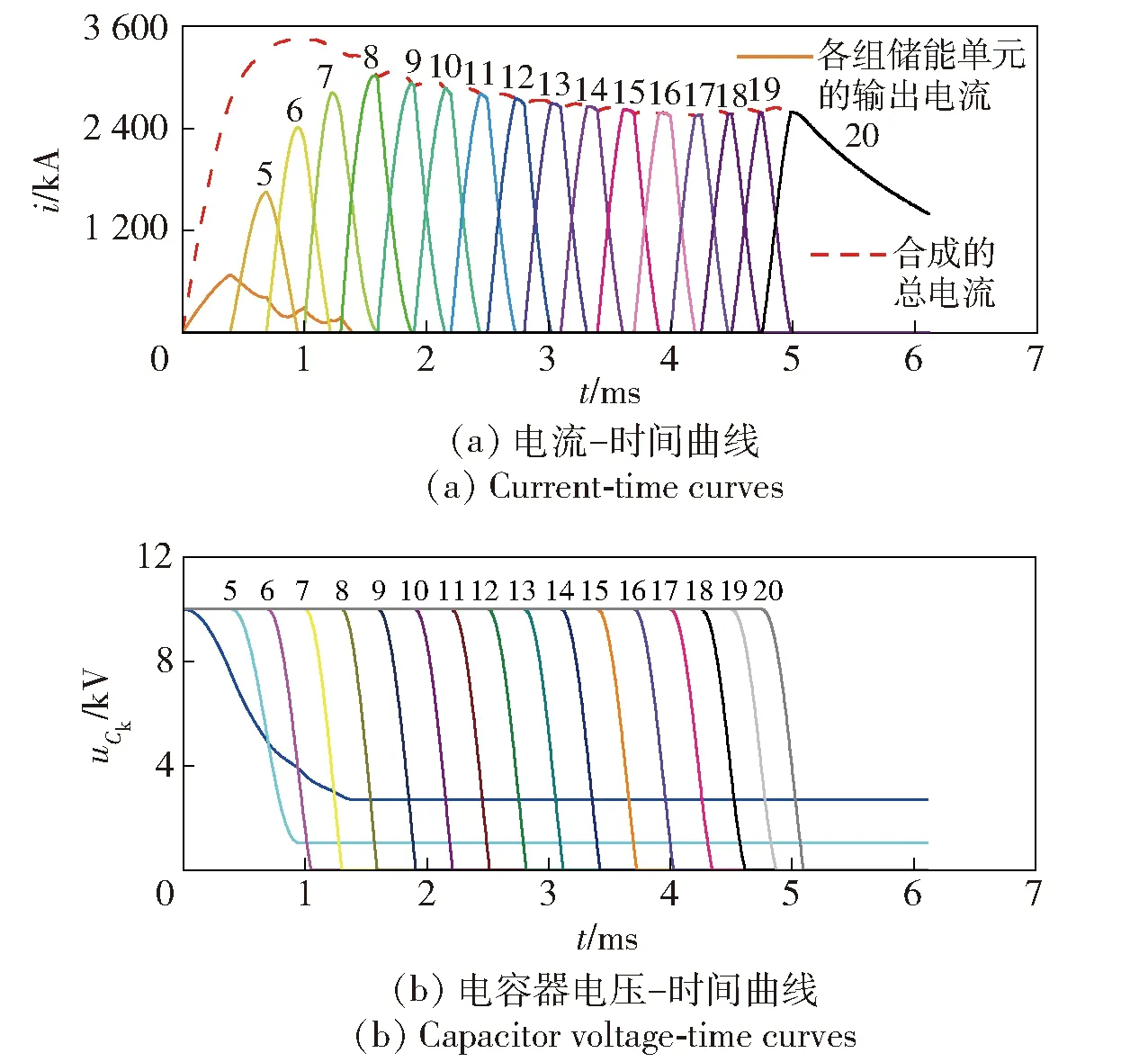
图4 电流和电容器电压曲线Fig.4 Current and capacitor voltage curves
在图4(a)电流- 时间曲线的上升沿,即0.75 ms之前,只有第1~5组单元放电,它们的电容器电压- 时间曲线显示这部分单元的电容器上存在着剩余电压,表明它们存储的电能并未完全释放。文献[20]分析了这种现象的产生机理,认为它与晶闸管开关的关断特性以及发射初期较高的负载电压有关。图5所示负载电压(即炮尾电压)Ub-时间曲线显示了发射初期的高幅度电压以及时序放电所造成的电压波动。
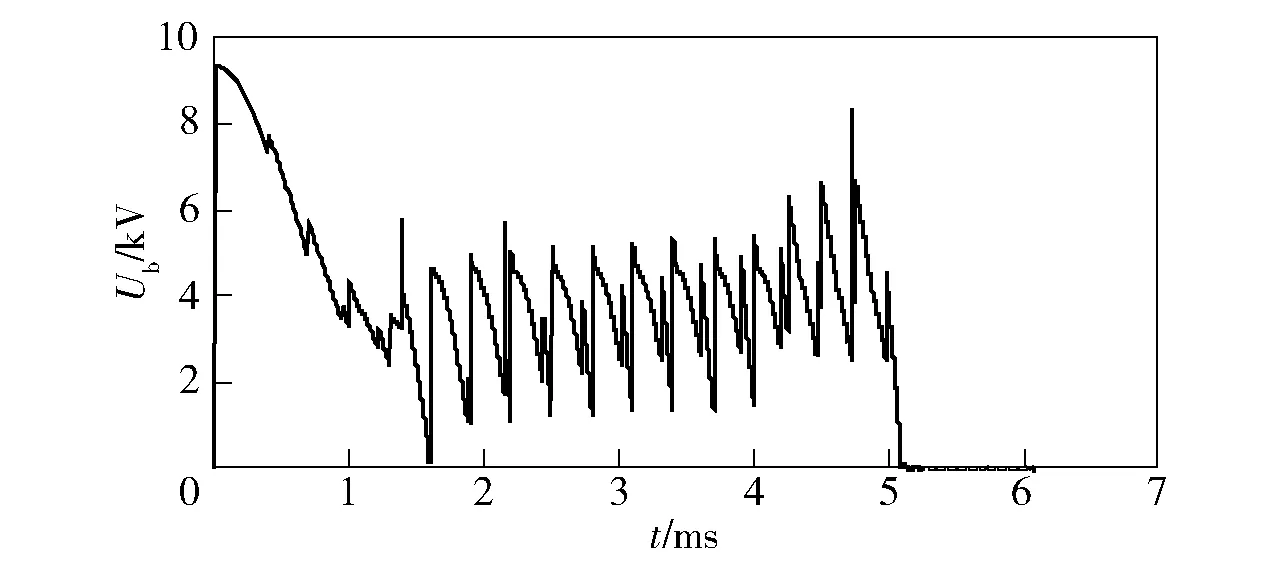
图5 负载电压- 时间曲线Fig.5 Voltage-time curve of load
3.2.2 电磁场计算结果
图6为轨道、电枢、弹体等导体上的电流密度J序列分布。高电流密度区主要集中在电枢及其后部的一段轨道上,这与趋肤效应及速度趋肤效应有关。另外,从图6中可以看出,电枢和弹体沿发射方向运动,它们在不同时刻所到达的位置是通过结构场与电磁场的耦合计算获得的。

图6 电流密度的序列分布图Fig.6 Sequential contours of current density
由于ILP会携带引信、装药等敏感部件,需要考虑电磁场对它们的影响。弹丸的壳体一般为导电材料,在脉冲磁场下会感应出涡流。将图6的电流密度降低2个数量级,单独显示弹体上的电流密度分布,如图7所示。在刚开始放电时(t=0.005 ms),弹体上出现了明显的感应电流,并且在靠近弹底的地方幅度较高。随着时间推移,弹体上的感应电流逐渐变小。
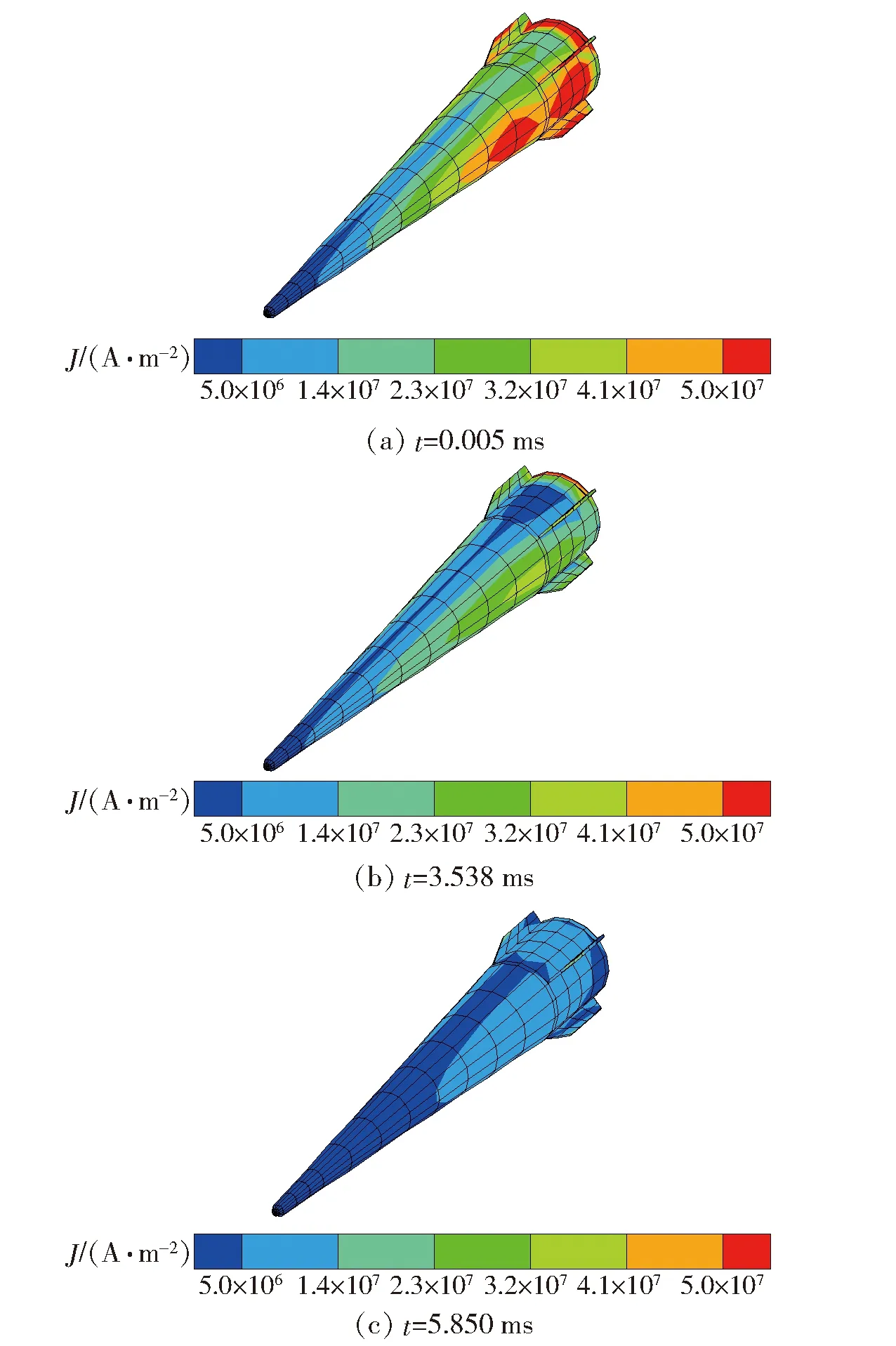
图7 弹体上的电流密度序列分布Fig.7 Sequential contours of current density on projectile
图8所示弹体表面的磁通密度B分布,呈现出弹底高、弹尖低的分布特征。电枢和轨道组成的导电通路为非轴对称结构,决定了弹体上的磁场也是非轴对称的。在发射过程中,尽管磁通密度的幅度会有变化,但是分布模式没有发生明显的改变。通过对瞬态磁场的计算,可以为弹上敏感部件安装位置及方向的设计提供参考。
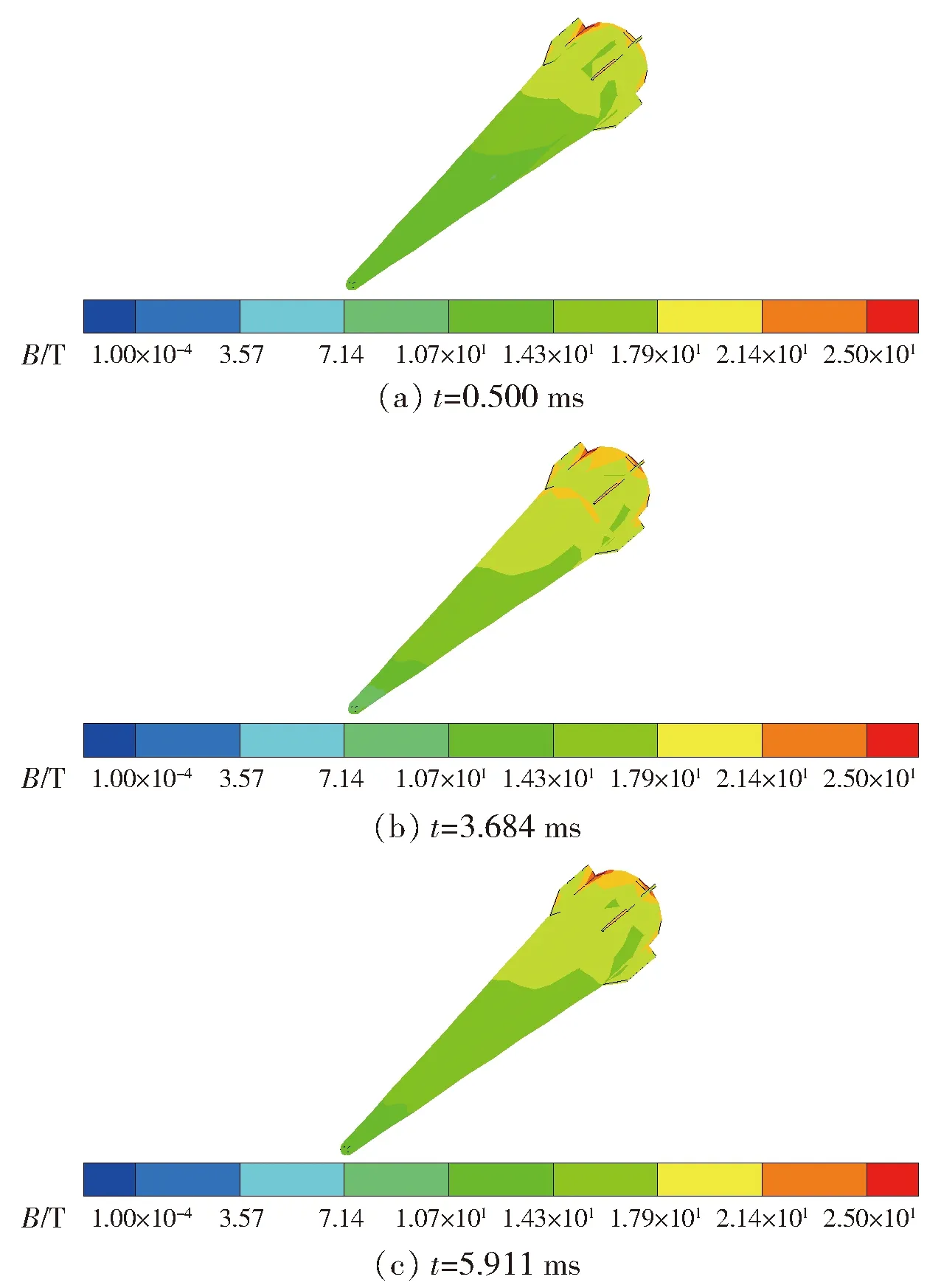
图8 弹体的磁通密度序列分布图Fig.8 Sequential contours of flux density on projectile
电磁场计算的核心功能之一是获得作用于电枢的电磁力。电磁力的三维分布特征在文献[21]中曾作过讨论,不再赘述,这里主要讨论电磁力的合力。在电枢上,通过对电磁力密度的积分,可以获得沿发射方向的合力F.根据
(16)
可以计算出轨道的等效电感梯度L′.另外,根据(9)式~(12)式,从磁场储能的角度也可以计算出电感梯度L′1.将两种方法得到的结果列于图9.由图9可见,在5.0 ms之前,两条曲线是基本吻合的,但5.0 ms后,虚线表示的由受力计算出的等效电感梯度L′2有所下降,这段时间恰恰处于电流的下降沿,表明电枢的电磁力分布可能受到电流降低的影响而发生了变化。
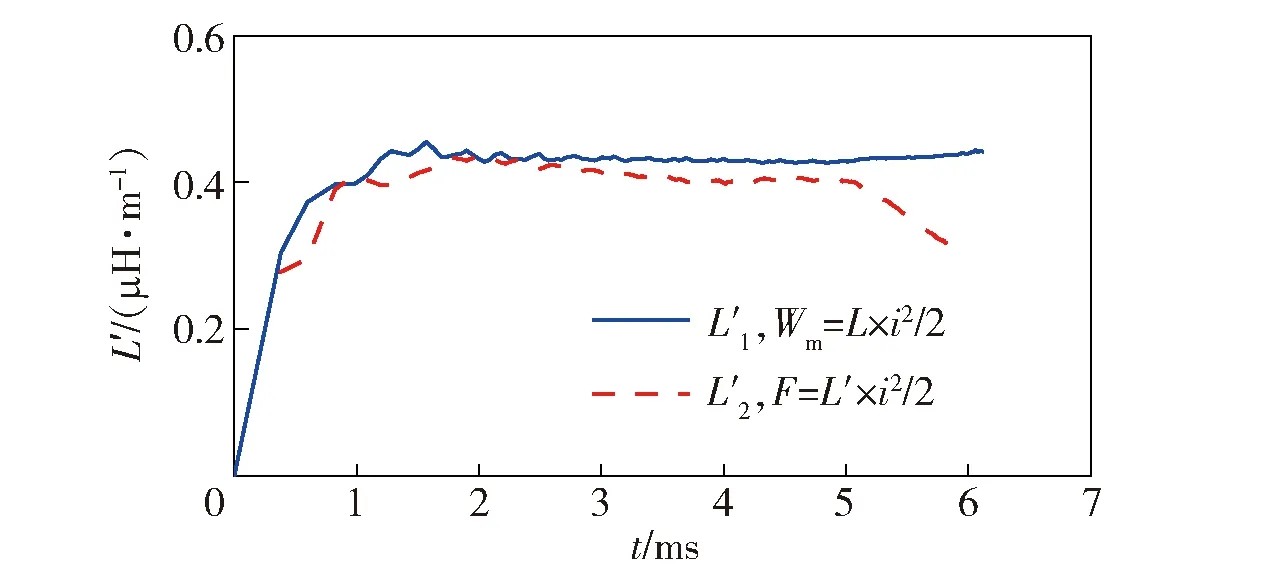
图9 电感梯度随时间的变化曲线Fig.9 Variation of inductance gradient with time
3.2.3 热场计算结果
电流在导体内产生的焦耳热不断累积,使温度升高。图10为ILP到达炮口时的电枢和弹体的温升分布对比。由于导致温升的热源主要来自于电流密度所产生的焦耳热,而且在短短几毫秒的发射周期内,热量来不及充分扩散,因此温升分布呈现出明显的三维特征,在图10(a)中表现得尤其明显,电枢上的局部温升超过了600 K,最大温升区位于电枢的喉部和电枢臂的尾端,与图6的电流密度分布情况相一致,体现了电磁场对温度场的作用。图10(a)的电枢温升分布表明,电枢喉部和电枢臂是潜在的易损伤部位,在发射试验中经常会出现电枢喉部的磁锯损伤和电枢臂磨损现象,与电枢温升的分布特性有一定关系。
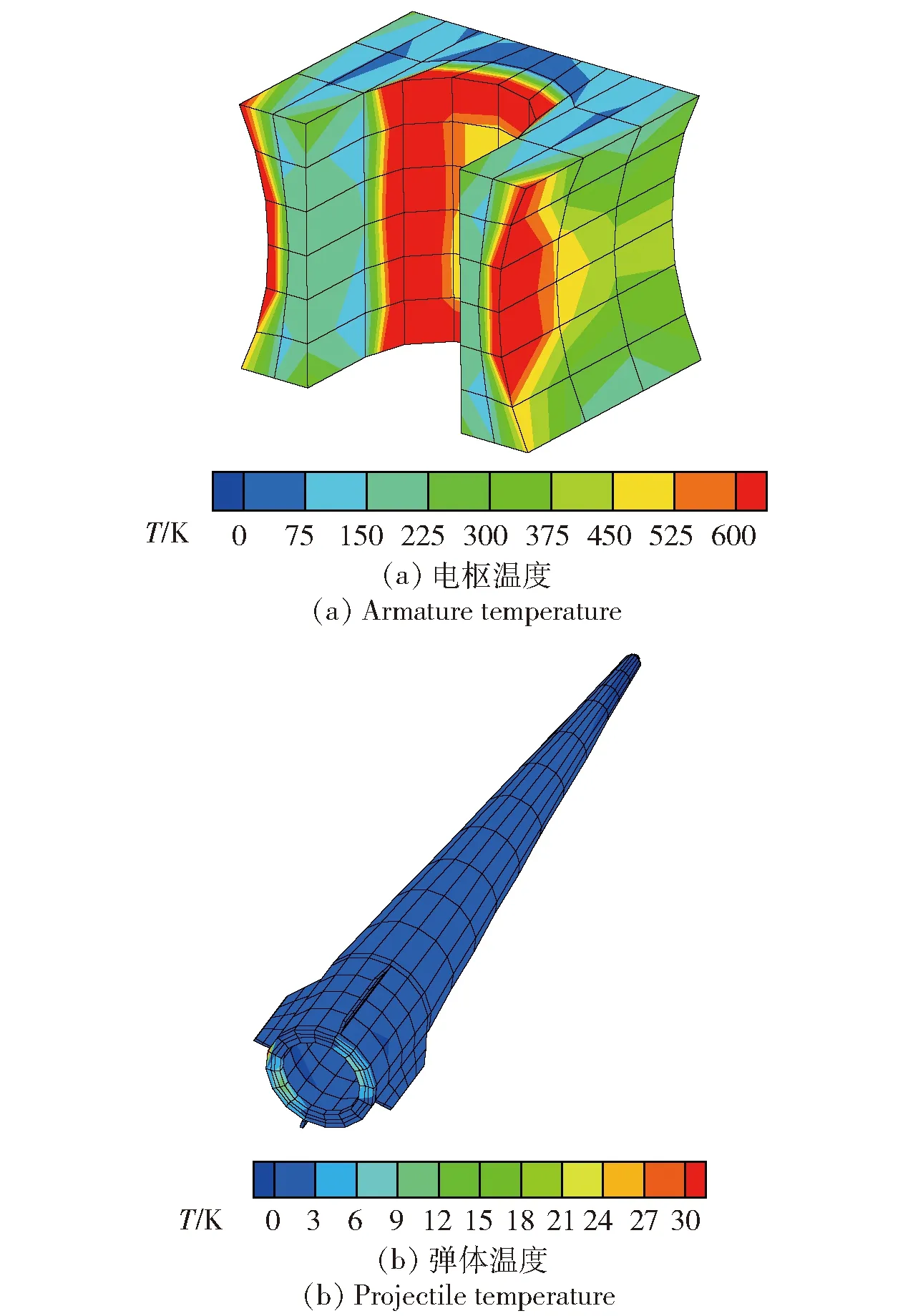
图10 电枢与弹体的温度分布Fig.10 Temperature contours of armature and projectile
由于弹体上的电流密度比电枢和轨道上的电流密度低几个数量级,相比之下,图10(b)所示弹体上的温升要小得多,最大温升区域位于弹底,由感应电流所导致。
3.2.4 结构场计算结果
结构场通过对连续介质力学方程组的求解,一方面追踪ILP的膛内运动,并将每一时间步的位移和速度及时回馈给电磁场和温度场,用于更新在ILP运动情况下的有限元网格构型;另一方面计算结构部件的微小变形、运动以及部件之间的相互作用,以获得对结构设计有重要参考意义的应力参数。图11为不同时刻的应力分布,图11中显示的是发射器和ILP的1/2模型。发射器和ILP内的应力主要源自于电磁力,由于电磁力产生于载流导体,随着电枢的运动,载流轨道的长度不断增加,发射器的高应力区也在不断扩大。另外,当t分别为3.447 ms和5.091 ms时,不仅ILP右侧的绝缘体上呈现出不均匀的应力分布,而且ILP左侧的一段发射器上也有应力区在发展,这与应力波在发射器内的传播有关。
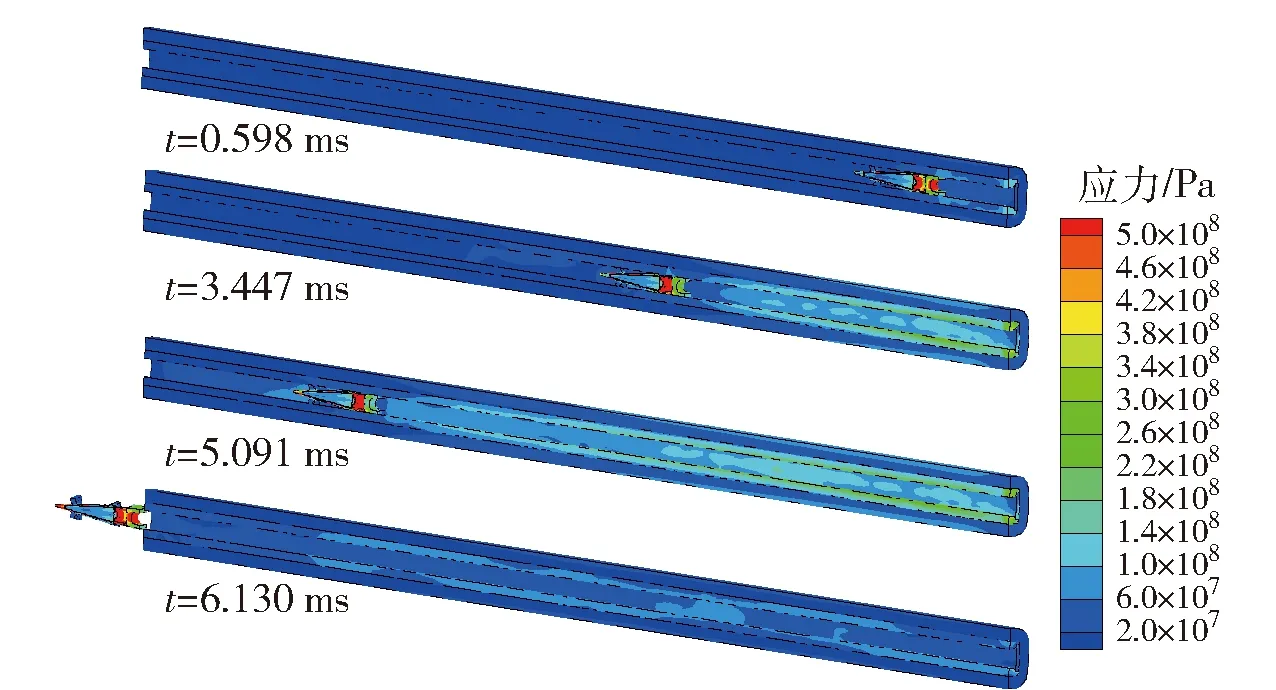
图11 发射器和ILP的应力分布与演化Fig.11 Distribution and evolution of stress on launcher and ILP
图12为ILP上的应力分布。由图4的电流曲线可知0.978 ms时电流最大,意味着电枢受到的电磁力最大,ILP承受的过载最大,因此该时刻的应力幅度最高,如图12(a)所示。在随后的两个时刻中,由于电枢的推进力主要作用于弹丸壳体,而且其承力截面比较小,因此最大应力区位于弹丸的壳体上。从图12(b)的ILP剖面图上可以看出弹丸内部装药上的应力分布,它底部的应力最大,能够达到百兆帕量级。图12的应力分布呈现出一定的对称性,而且三维分布特征在各个时刻表现得都很明显,其产生原因是多方面的,以电枢为例,既与电磁力的三维分布有关,也是整个系统在电磁力作用下的结构响应结果。

图12 ILP的应力分布与演化Fig.12 Distribution and evolution of stress on ILP
ILP及发射器的各部件组成了一个多体动力学系统。尽管发射过程中弹丸会发生变形和姿态改变,通过对模型网格的积分,仍可以得到其质心的运动规律。图13为发射过程中弹丸的位移x和速度v随时间的变化曲线,图14为弹丸的横向位移d和绕质心的转动角度ω的变化曲线。这些曲线表明弹丸在膛内存在多个自由度的运动,尤其是横向运动和摆动,尽管幅度很小,但也有可能在发射阶段产生横向过载,影响发射稳定性和安全性,这些因素在ILP的设计阶段应予以考虑。
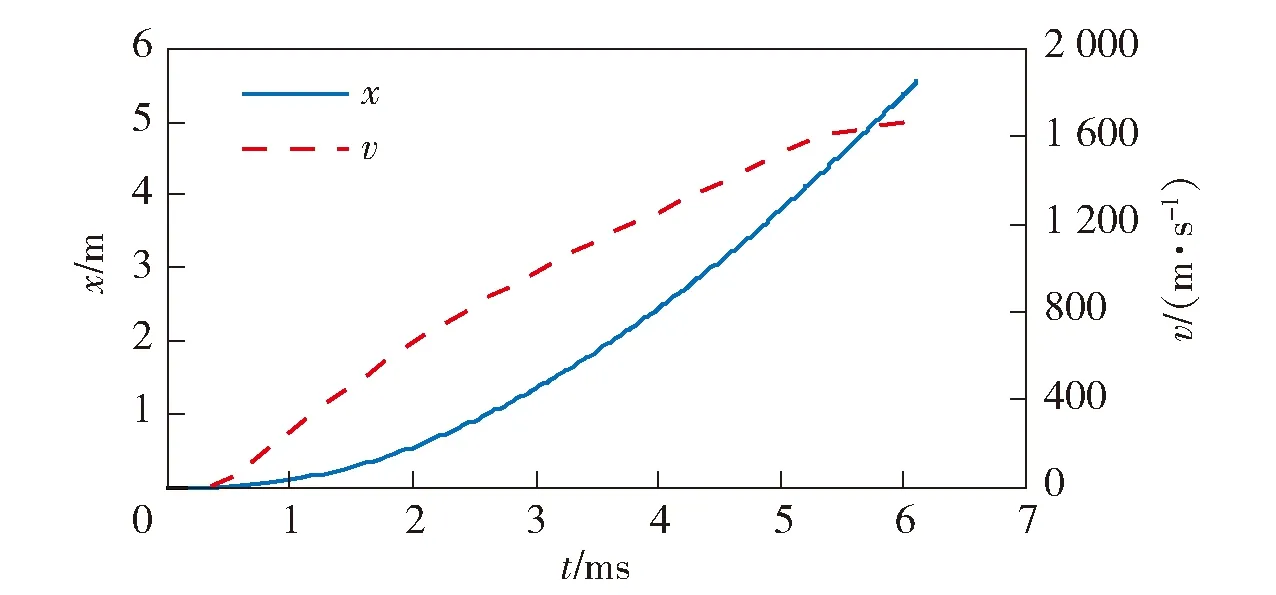
图13 弹丸的速度和位移曲线Fig.13 Velocity and displacement curves of projectile
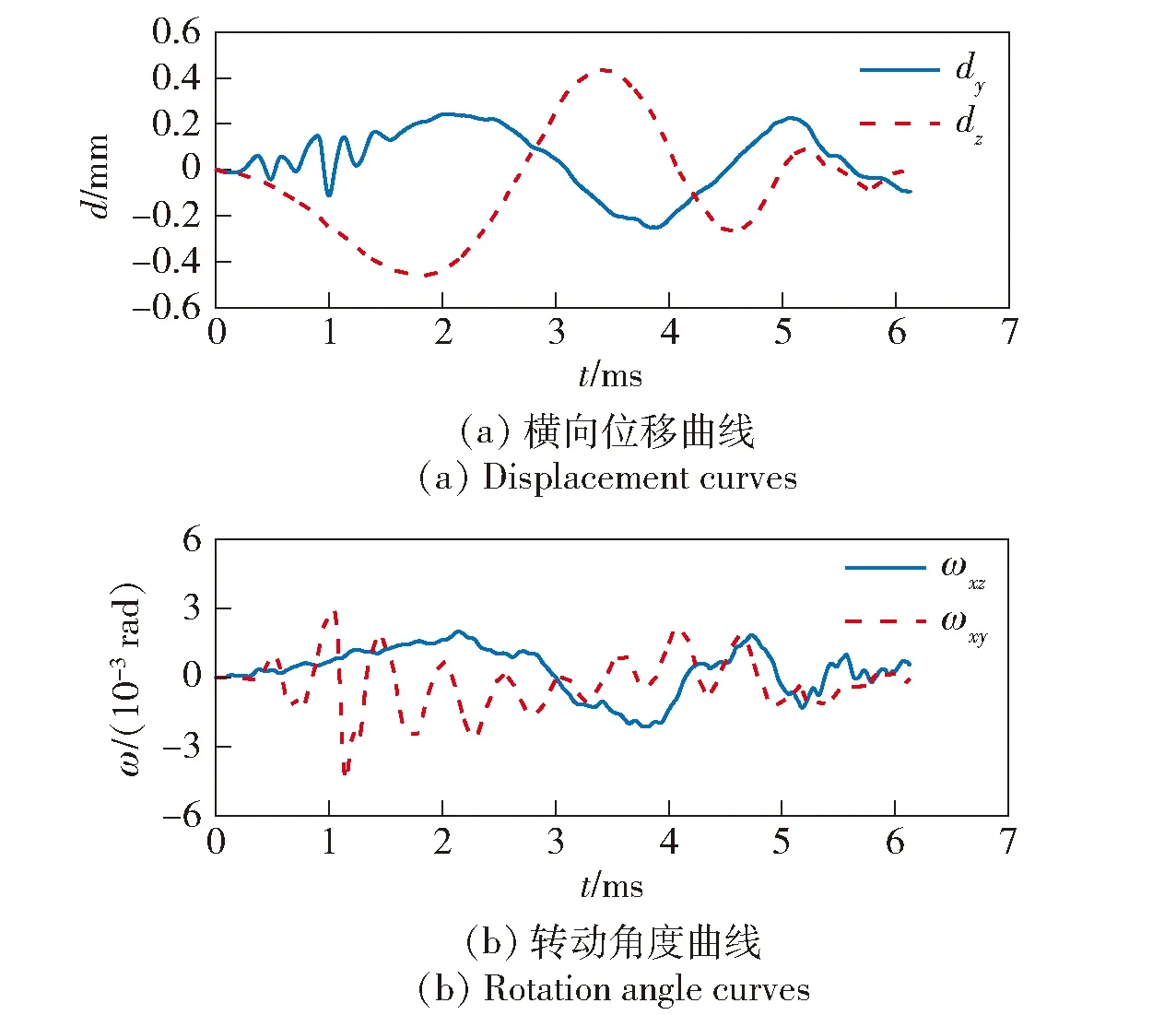
图14 弹丸的横向运动和摆动曲线Fig.14 Lateral motion and balloting curves of projectile
ILP的横向运动也反映在表2所示接触压力p分布上。表2中列出了4个时刻的电枢- 轨道接触面压力云图,可以看出接触压力并不是严格对称分布的,与发射过程中各部件的变形以及接触碰撞有关。
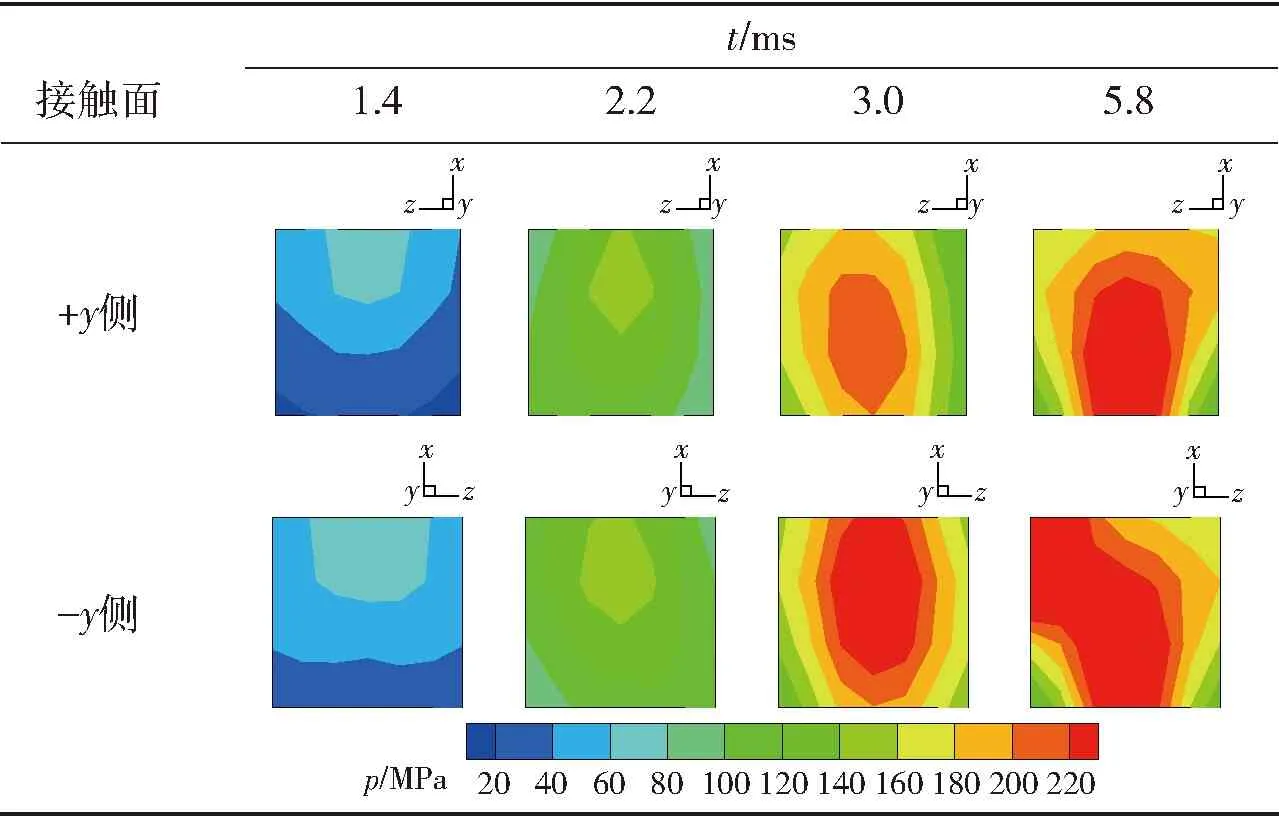
表2 电枢- 轨道接触面上的压力分布Tab.2 Pressure distribution on armature-rail contact surface
上述电磁轨道炮算例表明,求解器通过焦耳热和电磁力载荷在物理场间的实时传递以及网格构型的实时更新,实现了电磁场、温度场和结构场的耦合计算,不但能够用电流、电压、电阻、电感、速度等集总参数从系统的角度描述发射过程,而且能够用电流密度、磁通密度、温度、应力等场量从细节处描述各部件的物理场分布及演化,甚至可以捕捉到摆动、接触碰撞、应力波等因素带来的发射过程非理想特性,计算所获得的信息可以为电磁轨道炮的设计提供参考。
4 同步感应线圈炮发射过程数值仿真研究
4.1 单级线圈炮
为验证求解器在线圈炮数值仿真中的可用性,首先针对单级线圈炮,与文献[22]给出的理论和实验结果进行对比。算例的结构尺寸如图15所示,电枢为铝筒,其电导率为3.0×107S/m,线圈由60匝导线绕成,驱动电流如图16所示。
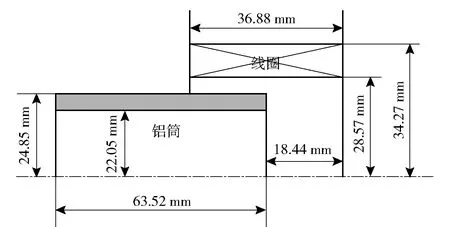
图15 单级线圈炮结构示意图Fig.15 Schematic diagram of single-stage coilgun
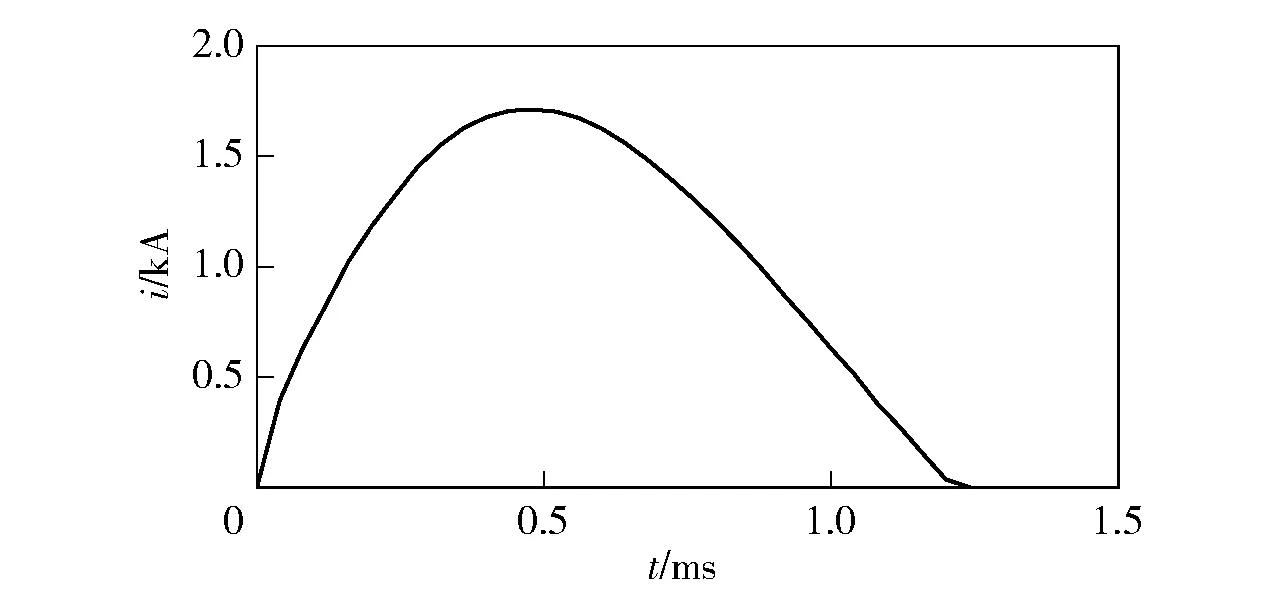
图16 单级线圈炮的驱动电流波形Fig.16 Current waveform for driving the single-stage coilgun
图17列出了本文求解器的计算结果与文献[22]结果的对比。由图17可见:3条曲线基本吻合,发射初期,电枢受到前向推动力,速度迅速上升;在电枢将要离开线圈时则会受到拖拽力作用,使速度有所下降,之后作匀速运动。
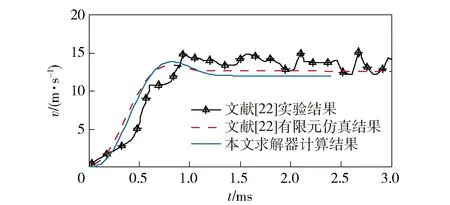
图17 计算和实验结果的对比图Fig.17 Comparison of calculated and experimental results
图18从左至右分别给出了发射初期的电流密度、磁通密度,以及电磁力密度的矢量图。从图18(a)的电流密度矢量可以看出,电枢局部感应出与线圈电流密度方向相反的电流;从图18(b)的磁通密度矢量可以看出,磁通密度较大的区域位于电枢和线圈之间;从图18(c)的电磁力密度矢量图可以看出,尽管电枢和线圈都受到了电磁力的作用,但电枢上的电磁力主要位于与线圈交叠的地方。
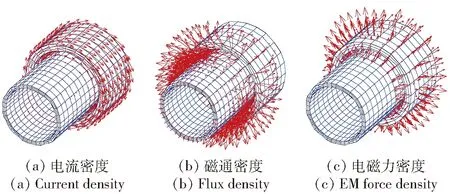
图18 电流- 磁场- 电磁力的矢量图Fig.18 Vectors of current density,flux density and EM force density
该算例结果表明,本文的求解器可以用于处理同步感应线圈炮这种含有运动导体的涡流场问题。
4.2 多级线圈炮
仿照文献[23]的线圈炮尺寸,建立10级线圈炮的计算模型如图19所示。线圈由20匝导线绕制,电枢为铝制圆筒,设置为弹塑性材料,电枢与线圈之间为绝缘的导向管,设置为正交各向异性弹性材料,它与线圈紧密接触,而与电枢之间保留了1 mm的间隙。各级线圈的驱动电流如图20所示。
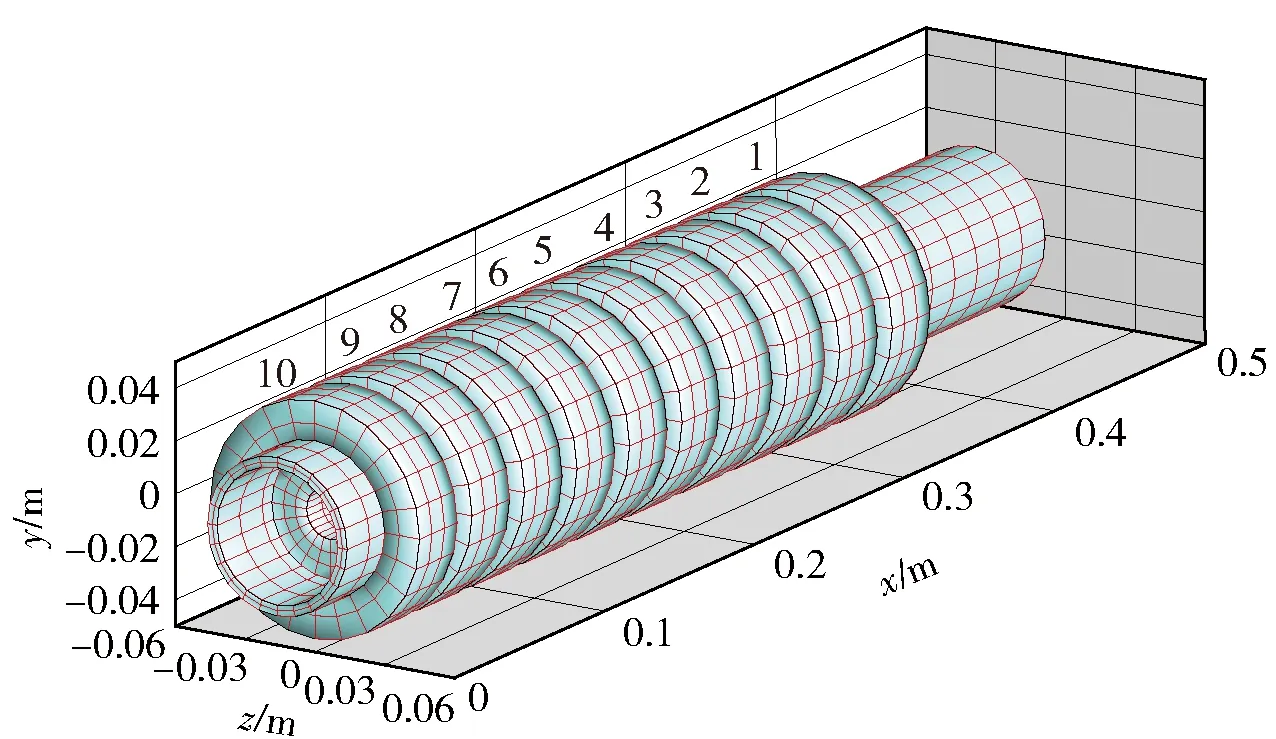
图19 多级线圈炮模型Fig.19 Model of multi-stage coilgun
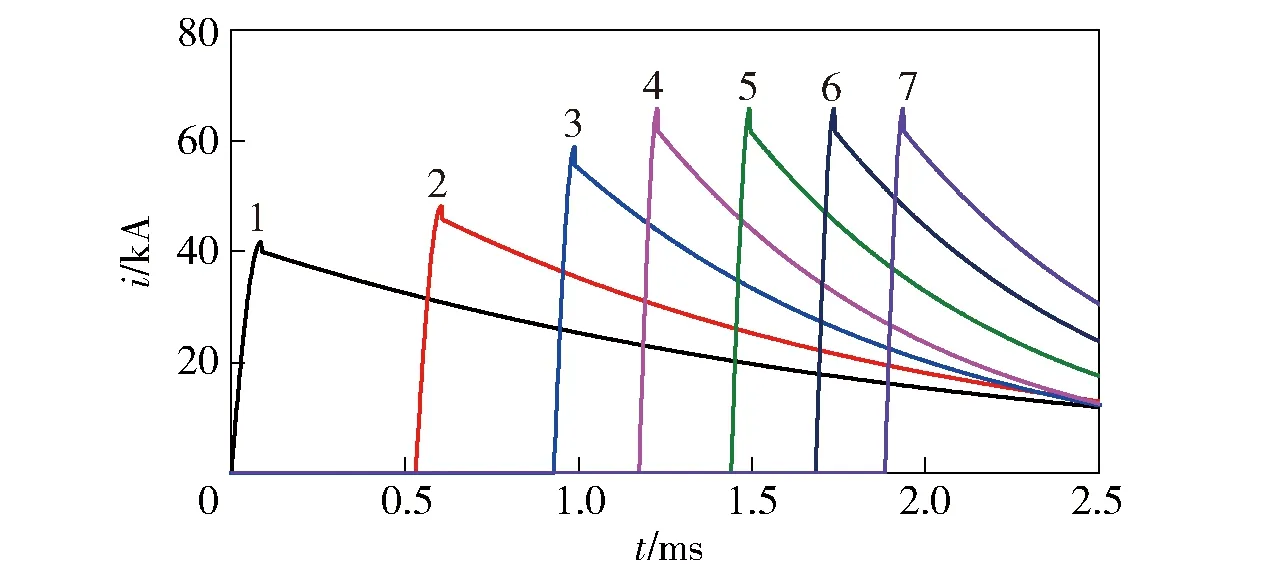
图20 各级线圈的激励电流曲线Fig.20 Driving current curves of coils
图21为第1~4级线圈逐次放电时的电流密度分布图,图中显示了线圈和电枢的3/4部分。由于线圈由多匝导线绕成,线圈上的电流密度均匀分布,而电枢上呈现出了密度不均的电流分布,高电流密度区出现在电枢的外侧、靠近正在放电线圈的位置。
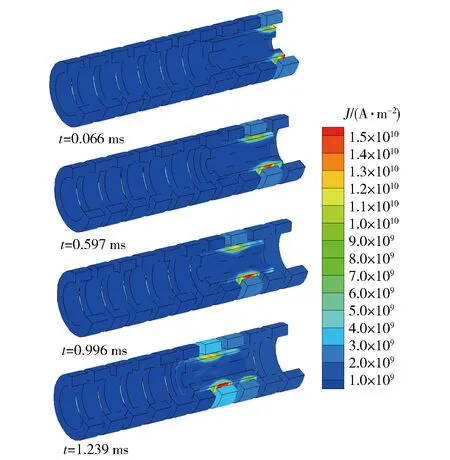
图21 电流密度的序列分布Fig.21 Sequential contours of current density
图22为线圈、电枢和导向管上的应力分布。由图22可见,在初始的0.178 ms,电枢上的高应力区位于其尾部,随着线圈的逐个放电,电枢上的应力分布也发生了改变。导向管上存在着应力分布,在2.270 ms时幅度比较大,这可能是电枢在较高速度下与导向管发生碰撞而造成的。

图22 应力的序列分布Fig.22 Sequential contours of stress
图23为电枢速度- 时间曲线。曲线上有多个鼓包,对应着电枢经过每一级线圈时所经历的加速和减速过程。另外,该曲线是通过质心位移对时间的差分来计算的,由于电枢在发射过程中存在着变形和姿态的改变,计算出的速度- 时间曲线有些振荡,特别是速度超过100 m/s后振荡更明显。
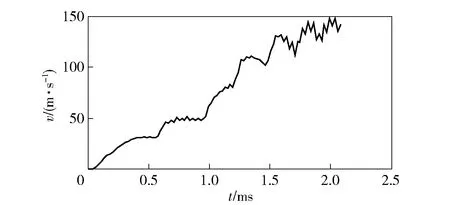
图23 电枢的速度- 时间曲线Fig.23 Velocity-time curve of armature
由于电枢与导向管之间有1 mm的间隙,电枢会在管内摆动,并与管壁发生碰撞。图24显示了电枢的横向位移dy、dz的变化过程。
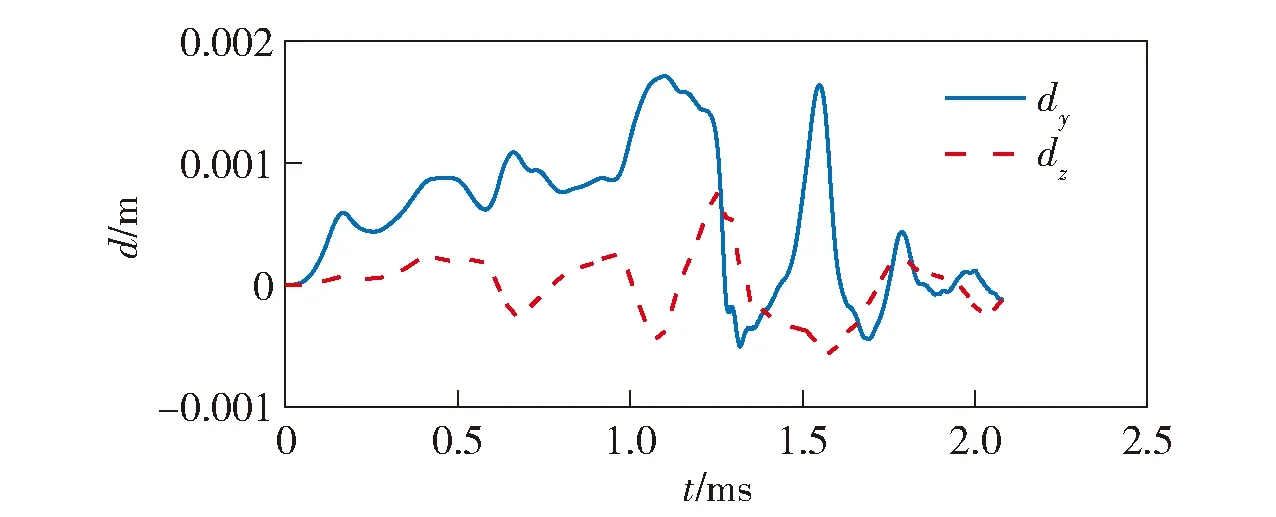
图24 横向位移曲线Fig.24 Lateral displacement curves
增加电流是提高电枢速度的途径之一,但带来的负面影响是造成电枢的变形。图25为将第1、2级线圈的放电电流峰值各自增加10 kA时出现的电枢变形。变形发生在电枢的尾部,变形模式与图26所示文献[24]的实验现象非常相似。

图25 大电流下的电枢塑性变形Fig.25 Plastic deformation of armature subjected to high current

图26 变形后的电枢照片[24]Fig.26 Photo of deformed armature[24]
上述算例结果表明,本文的求解器有能力处理同步感应电磁线圈炮问题,它对电枢在脉冲磁场作用下的运动、变形过程的刻画有助于为电磁线圈炮的设计提供参考依据。
5 结论
本文瞬态多物理场求解器基于电磁场、热场、结构场的动力学模型,通过多场耦合、场路耦合,实现了对电流扩散过程和趋肤效应、热传导过程和温升效应、结构动力学过程和多部件的力学接触与冲击效应的模拟,初步具备了针对电磁炮全系统、全尺寸、全发射周期的数值仿真能力。通过数值模拟,得出如下主要结论:
1) 电磁炮的发射过程是多物理场耦合、多部件相互作用下一个复杂的动力学过程。
2) 发射工况和发射性能与结构、材料以及激励条件之间具有密切的相关性。
3) 求解器可用于模拟动态发射工况,确定发射器、一体化弹的危险点,对设计方案进行强度校核,评价设计方案的可行性。求解器的计算功能全部采用Fortran源代码实现,因此具有良好的使用灵活性和功能可扩展性。
下一步,将结合电磁发射理论与技术的进展,继续提高多物理场仿真计算的精细化程度,另外还将拓展该求解器的应用方向,使其能在更多的工程技术领域发挥作用。

