超轻型火炮后大架缓冲机理及特性优化

张成，柳朝阳，顾克秋

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.32180部队，北京 100072)

0 引言

超轻型火炮是适应现代战争特点，以高战略、战役、战术机动性为主要特征的地面压制火炮。射击稳定性是超轻型火炮设计需要优先保证的约束条件。这类火炮平射或小射角射击时，架体相对地面的跳动量必须尽可能小，否则对火炮射击精度、结构强度可靠性、射速等性能都会带来不利影响，从而削弱其作战效能。

美国M777、中国AH4等超轻型火炮在下架与后大架之间设置了液压缓冲装置，有利于改善火炮的射击稳定性[1]。M777、AH4的后大架缓冲装置均采用缓冲器下置的布置方案。经发射动力学分析，这种缓冲器下置方案对提高射击稳定性效果不明显。

后大架缓冲器的布置方式、结构形式、设计参量与工作特性具有内在的关联性，研究这类缓冲器参量配置及其特性优化[2-5]，对于获得所需工作特性以改善火炮射击稳定性和结构受力，从而进一步提高轻型火炮的总体性能具有重要意义。而关于超轻型火炮后大架缓冲器的研究尚未见文献报道。

在有关缓冲器特性和设计方法研究方面，马星国等[6]将理想缓冲效率与实际缓冲效率的差值设为目标函数，利用遗传算法对缓冲器进行优化。李世康等[7]利用Isight集成多体动力学仿真软件ADAMS，采用最优拉丁超立方方法对缓冲簧设计参数进行灵敏度分析，并采用非支配排序遗传算法(NAGA-Ⅱ)对缓冲簧设计参数进行优化设计。姚养无[8]在分析缓冲器作用力对射击精度影响基础上，规划了后坐阻力的变化规律，大幅度减小了大口径狙击步枪发射时的后坐力。

本文针对某大口径超轻型火炮，探索性地提出一种后大架缓冲器上置方案，与已经出现的下置方案作对比分析研究，以加深对超轻型火炮后大架缓冲效能的认识；给出缓冲器正面设计的基础，通过全炮发射动力学分析来研究和揭示缓冲器上置和缓冲器下置两种布置方案对全炮射击稳定性的影响。针对缓冲器上置方案，研究以减小前大架跳高和缓冲力峰值为目标，运用发射动力学响应的Kriging代理模型和NSGA-Ⅱ，对缓冲器节制杆缓冲段外形尺寸参数进行优化设计[9-15]。

1 后大架缓冲器设计

1.1 后大架缓冲器功能解析

通常认为，在超轻型火炮(如M777)下架与后大架之间设置一个缓冲器(见图1)，可以使射击过程中后坐阻力作用于炮架时，下架与后大架之间有液压缓冲装置进行缓冲，从而改善火炮的射击稳定性。此外，液压缓冲器有利于缓解全炮振动，缓解架体疲劳损坏、提高架体使用寿命。本文研究涉及两种火炮结构：一为传统结构的A型(见图1)；二为具备某射击稳定性控制原理的B型(见图2)。

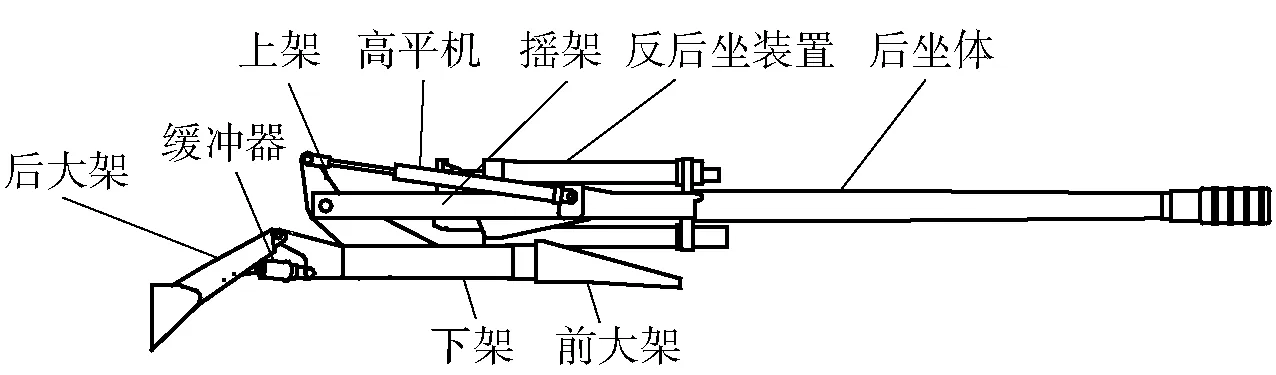
图1 A型火炮简图Fig.1 Schematic diagram of A-type artillery

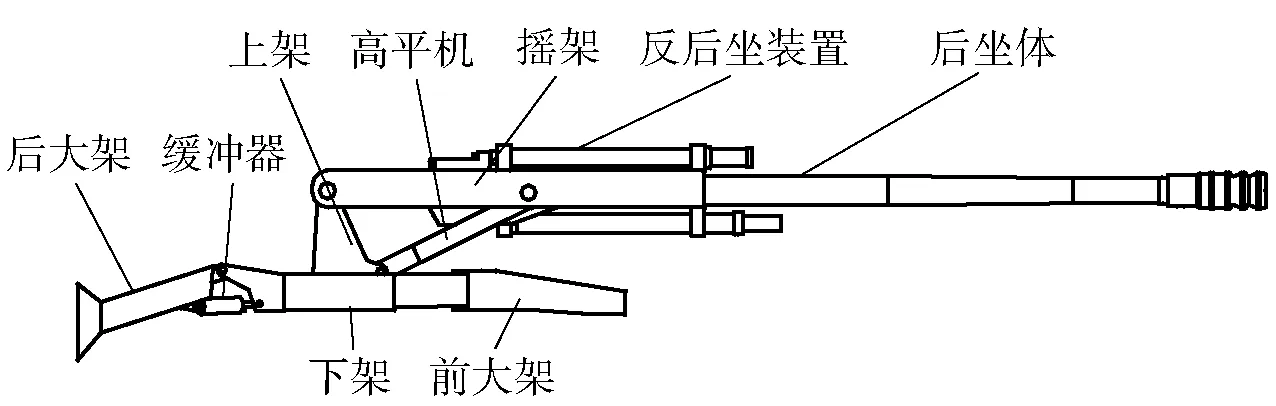
图2 B型火炮简图Fig.2 Schematic diagram of B-type artillery

1.2 缓冲器结构原理

后大架节制杆缓冲器结构如图3所示。由图3可见，缓冲器主要由碟簧、液压缸、活塞、节流阀门、节流挡板(见图4)和节制杆等构成。缓冲器局部结构如图5所示。火药燃气产生的压力通过架体进行传递，最后由下架经过缓冲器传递给后大架。下架带动缓冲器进行缓冲，缓冲器内碟簧被压缩为缓冲器复位积蓄能量，Ⅰ腔体积减小，腔内压力增大，将靠近复进节流挡板处的节流阀门冲开，使液体从节流挡板外流液孔流入Ⅱ腔，复进部分失去作用，由缓冲部分节制杆与节流挡板配合产生阻尼力；当缓冲结束后碟簧舒张，Ⅱ腔压力升高，将靠近缓冲节流挡板处的节流阀门冲开，缓冲部分失去作用，由复进部分节制杆与复进节流挡板相配合产生阻尼力。

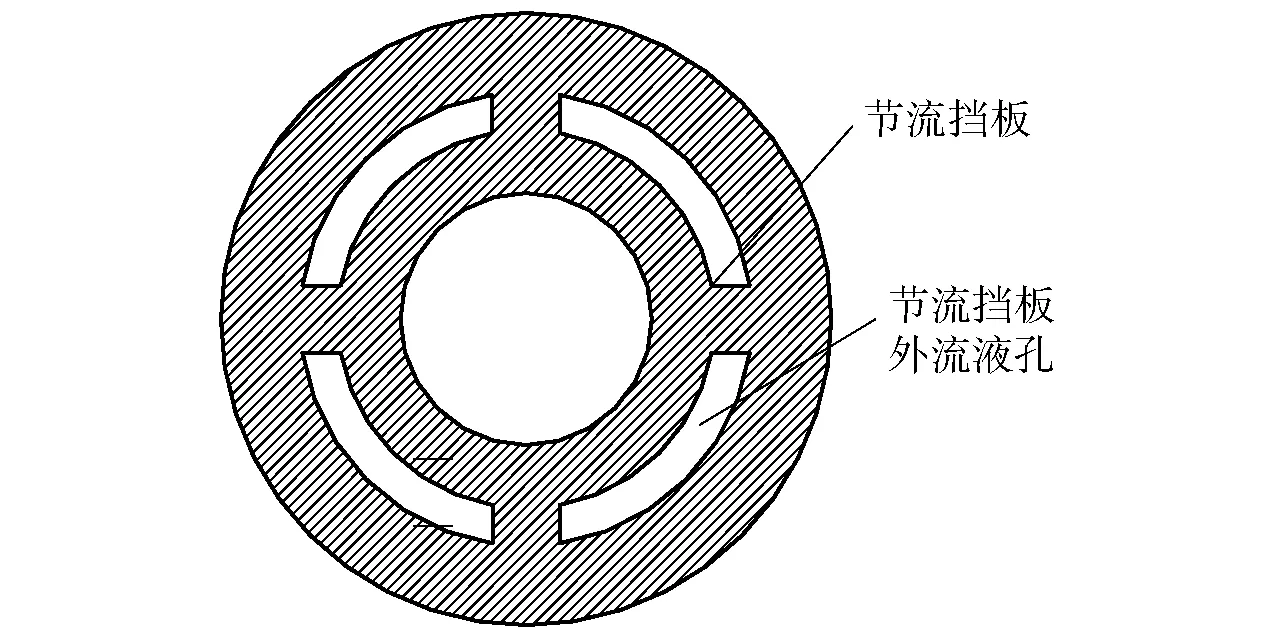
图4 节流挡板Fig.4 Throttle baffle

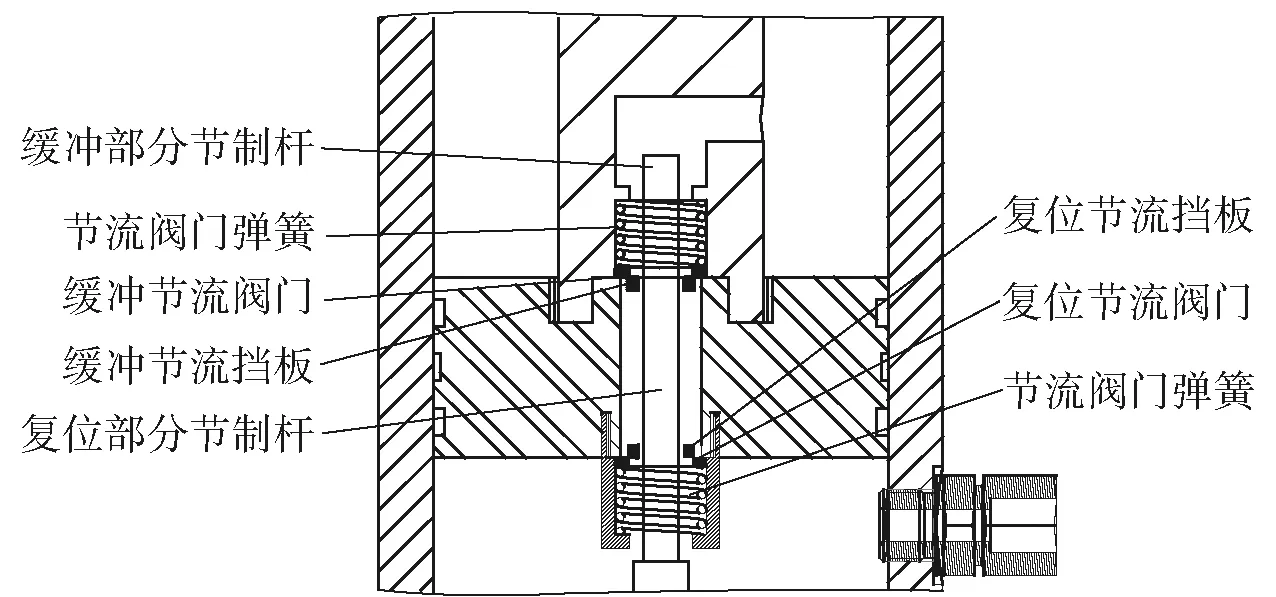
图5 缓冲器局部示意图Fig.5 Partial diagram of buffer

1.3 缓冲器参量设计

缓冲器安装布置方案不同，对缓冲特性的要求也不同，下面以B型火炮缓冲器上置方案为例，对缓冲器结构参数设计过程进行说明。参数设计的主要思路是通过全炮发射动力学仿真得到一组较优的阻尼力、弹簧刚度、预压力数据，然后根据得到的较优参数连同位移- 时间、阻尼力- 时间、速度- 时间关系函数，运用伯努利方程式设计和计算出后大架缓冲器节制杆尺寸参数及复位弹簧的结构参数。

1.3.1 设计的约束条件

1)缓冲器位移U<30 mm；

2)最大缓冲力Fmax≤120 000 N；

3)弹簧预压力F0>200 N.

1.3.2 缓冲器设计诸元变化范围

1.3.2.1 弹簧刚度系数的确定

缓冲力最大值不超过120 000 N.缓冲器位移不超过30 mm，根据这两个条件及公式F=kU(F为缓冲力，k为弹簧刚度)可初步确定弹簧刚度范围。弹簧刚度上限kmax=120 000 N/30 mm=4 000 N/mm.k下限为0 N/mm，弹簧刚度变化范围k∈[0 N/mm,4 000 N/mm].

1.3.2.2 弹簧预压力的确定

弹簧预压力下限F0 min=200 N，预压力上限取值为最大缓冲力的1/10，即F0max=12 000 N.预压力变化范围F0∈[200 N,12 000 N]。

1.3.2.3 阻尼力的确定

阻尼力需要满足的条件是在整个缓冲过程中阻尼力、弹簧弹力及预压力之和不大于120 000 N.其下限为0 N，上限为允许的最大缓冲力与最大预压力之差，即fxmax=108 000 N.阻尼力变化范围fx∈[0 N,108 000 N]。

1.3.3 碟簧及节制杆尺寸参数设计

在B型火炮缓冲器上置全炮刚柔耦合发射动力学模型基础上，通过Fortran子程序选取不同的预压力、刚度、阻尼进行试算。经仿真试算，选取弹簧预压力F0=2 000 N、弹簧刚度k=1 000 N/mm、阻尼系数c=500为一组较优参数。在这组较优参数基础上，进行缓冲器相关部件尺寸参数的设计。

根据弹簧预压力、弹簧刚度以及缓冲器总体尺寸进行碟簧尺寸参数的设计，其尺寸参数初步设计为碟簧锥高h0=2 mm，碟簧厚度δ=5 mm，碟簧外径do=90 mm，碟簧内径di=50 mm.

根据仿真试算选取阻尼系数c=500，其速度变化曲线与位移变化曲线如图6和图7所示。

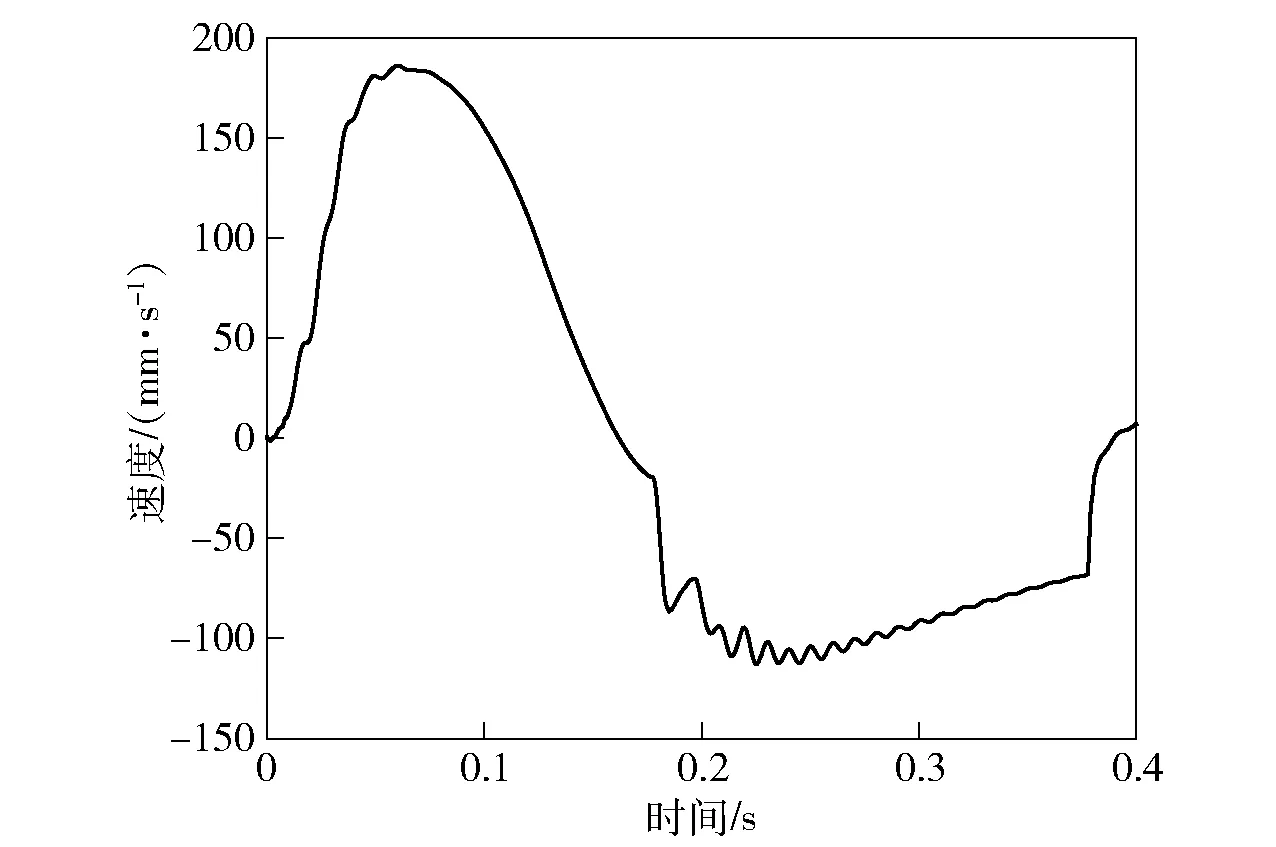
图6 速度- 时间曲线Fig.6 Speed-time curve

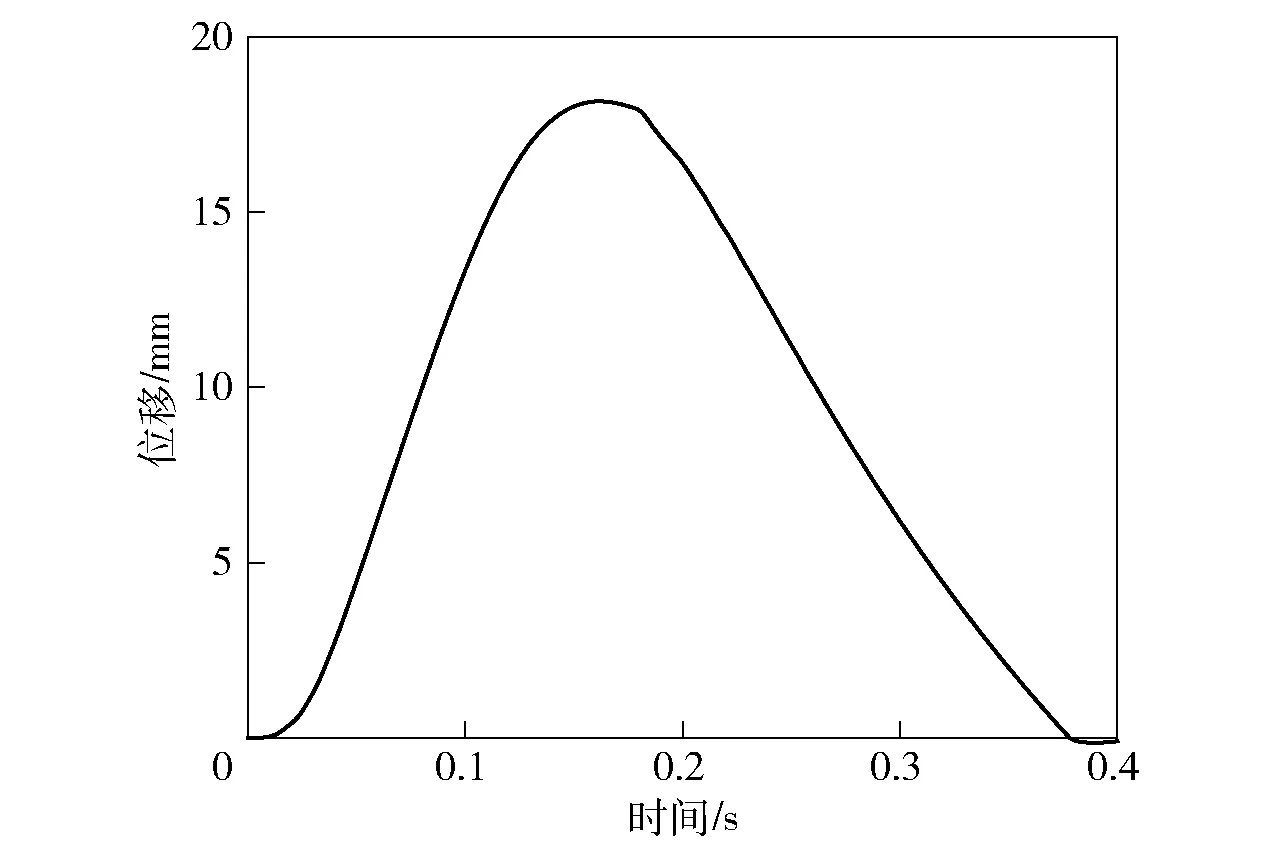
图7 位移- 时间曲线Fig.7 Displacement-time curve

根据速度- 时间曲线与阻尼力公式f=-cv(v为缓冲速度)可以得出阻尼力- 时间曲线，其变化规律如图8所示。由图8可知，从开始运动到0.168 s时缓冲器处于缓冲阶段，可根据阻尼力- 时间曲线图以及位移- 时间曲线图拟合出缓冲过程中阻尼力- 位移曲线，如图9所示。

图9 阻尼力- 位移曲线Fig.9 Damping force-displacement curve

在液压油密度ρ、活塞有效工作面积A0、液压阻尼系数K确定的情况下，根据(1)式和(2)式与阻尼力- 位移曲线，可以得到相应的流液孔面积- 位移曲线图，如图10所示。

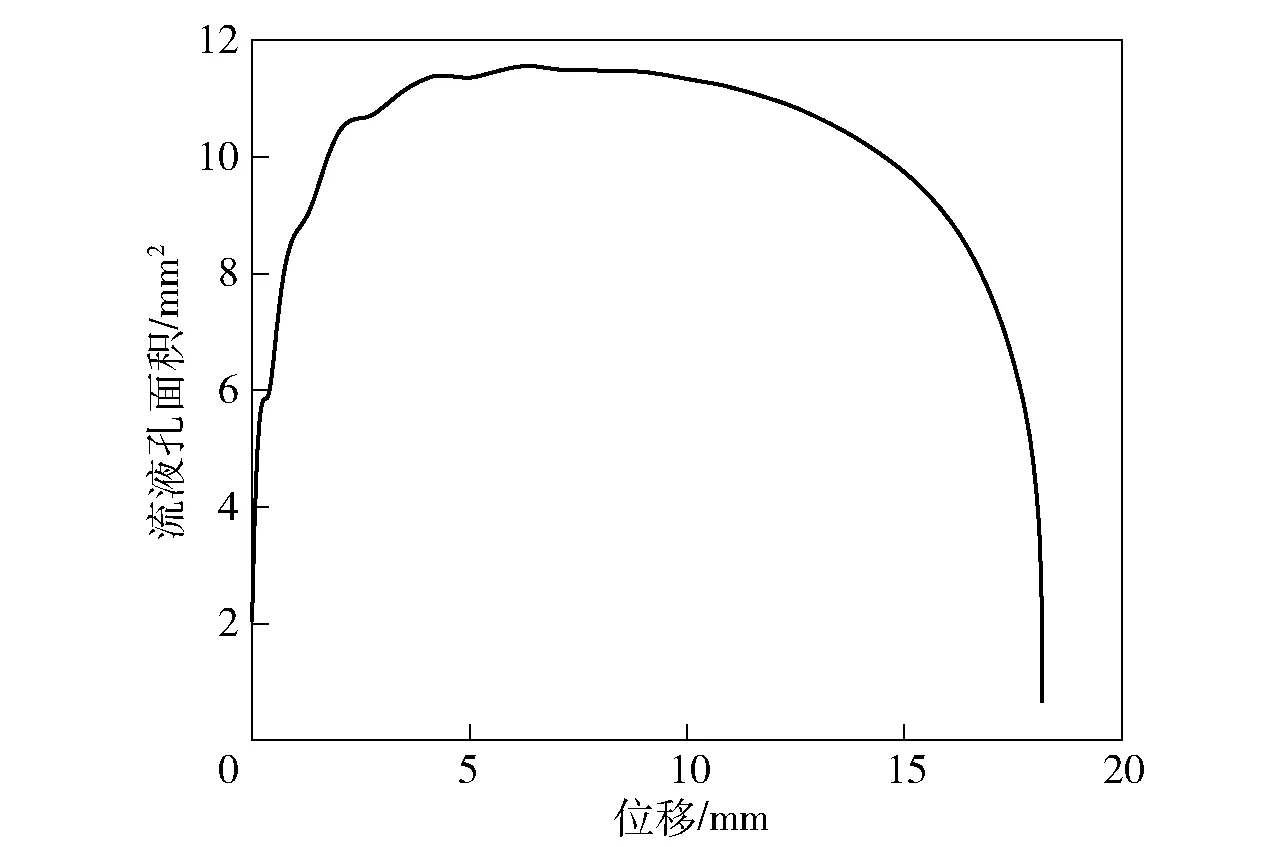
图10 流液孔面积- 位移曲线Fig.10 Flow hole area-displacement curve

(1)

(2)

式中：A为流液孔面积；f(A)为f与v2的函数关系式。

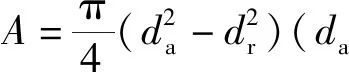
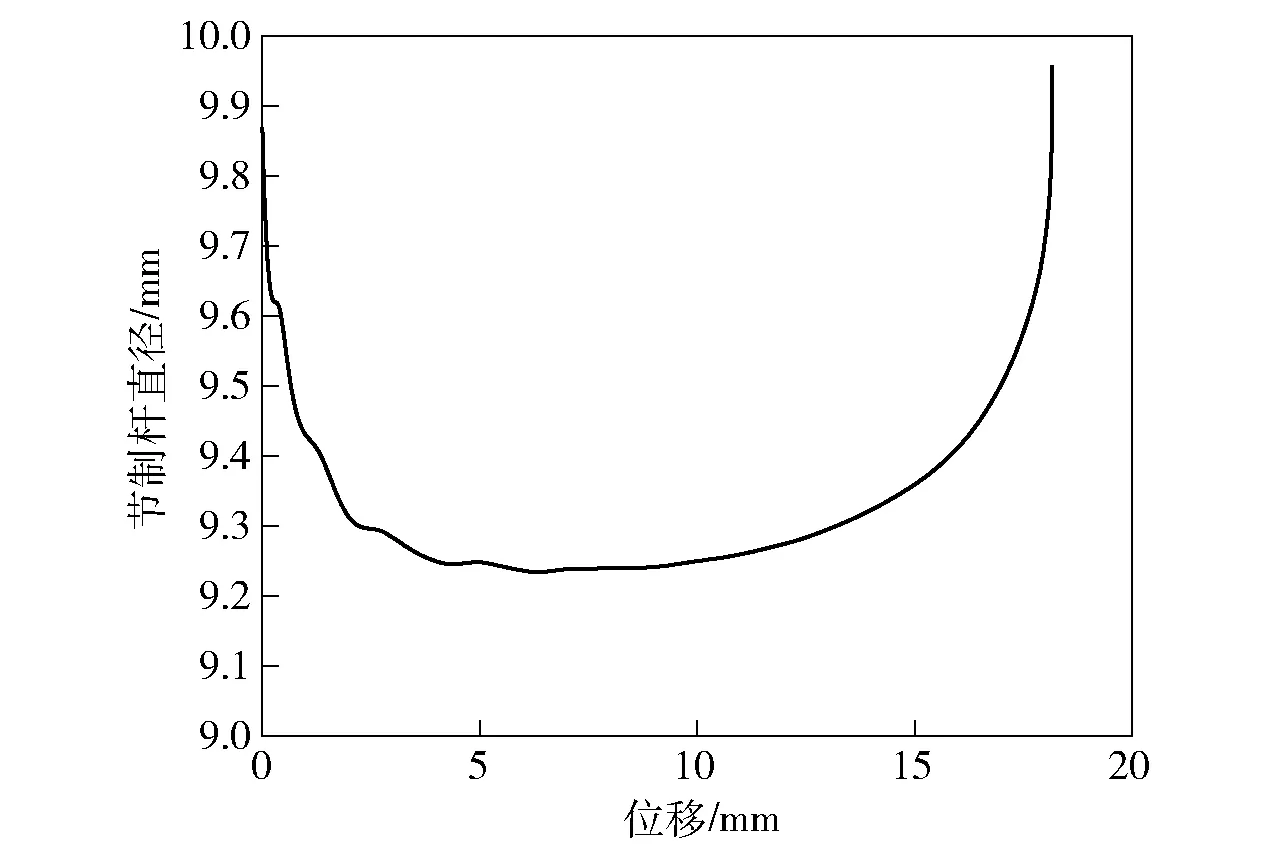
图11 缓冲部分的节制杆直径- 位移曲线Fig.11 Diameter-displacement curve of control rod in buffer part

根据图11曲线可推导出缓冲部分的节制杆散点数据，如表1所示。

表1 缓冲部分的节制杆散点数据Tab.1 Scatter data of control rod in buffer part mm

同理可推导出复位部分的节制杆直径- 位移曲线图，如图12所示。根据图12可推导出复位部分节制杆散点数据，如表2所示。

表2 复位部分的节制杆散点数据Tab.2 Scatter data of control rod in reset part mm

通过正面设计初步确定复位弹簧各结构参数以及节制杆部分直径数据，通过编写子程序进行缓冲力的反面计算。

2 缓冲器布置方案及动力学分析

2.1 两种缓冲器布置方案

A型超轻型火炮一般采用缓冲器下置的布置方案，如图13所示，缓冲过程中由缓冲器提供推力。本文提出缓冲器上置布置方案如图14所示，在缓冲过程中由缓冲器提供拉力。通过全炮发射动力学仿真，对两种布置方案的作用效果进行分析对比。

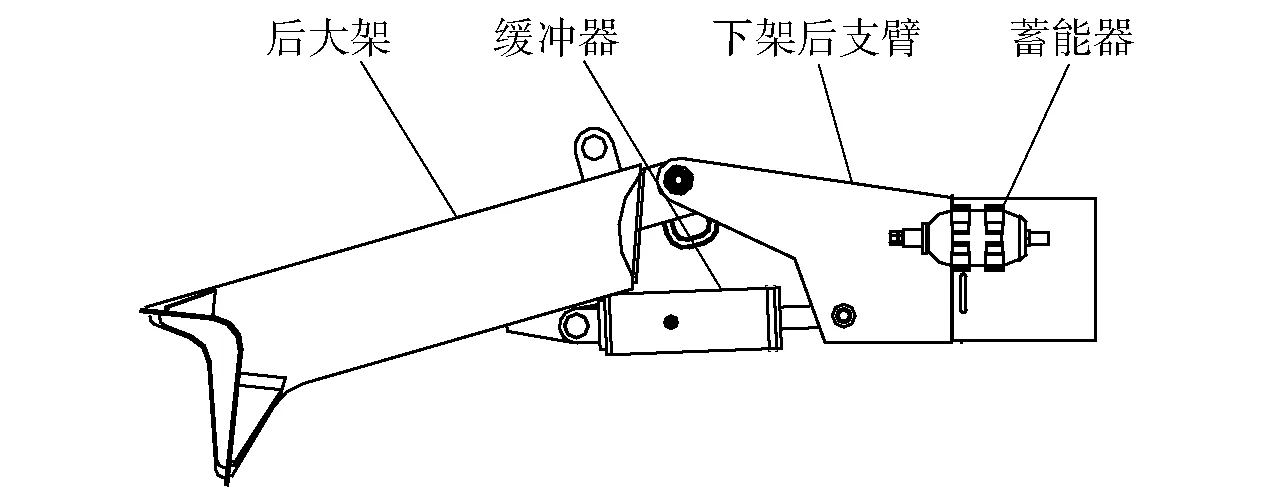
图13 缓冲器下置示意图Fig.13 Schematic diagram of buffer underneath backtrail

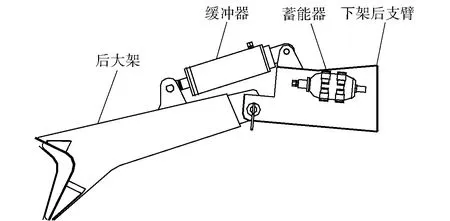
图14 缓冲器上置示意图Fig.14 Schematic diagram of buffer on top of backtrail

2.2 全炮刚柔耦合发射动力学建模

采用刚柔耦合有限元法进行发射动力学建模和动态响应特性分析。模型中含刚性体和有限元柔性体两种基本构件。采用刚性体，目的是提高计算效率、缩短仿真和优化计算周期。

A型火炮前大架、后大架采用壳体单元，考虑其柔性支撑对全炮射击稳定性的影响，其余部分采用刚性体建模，在其质心处赋予其质量及转动惯量。后坐体与摇架之间采用滑移副模拟后坐体后坐复进运动；摇架与上架之间采用耳轴连接，耳轴采用复合连接器模拟，赋予其除转动方向外其余5个方向等效刚度与阻尼；高平机采用梁单元模拟；上架与下架之间通过复合连接器模拟立轴连接，赋予连接器6个方向刚度与阻尼；下架与前大架采用铰链副连接，并在动力学计算时约束其转动方向自由度；当采用缓冲器上置方案时，下架与后大架下半部分采用铰链副连接，上半部分采用轴向连接器连接；当采用缓冲器下置方案时，下架与后大架上半部分采用铰链副连接，下半部分采用轴向连接器连接，通过Fortran用户子程序进行缓冲力的加载，从而实现发射动力学与缓冲特性的协同仿真。反后坐装置通过轴向连接器模拟，通过Fortran子程序实现复进机力、制退机力的加载，从而实现后坐特性与发射动力学的协同仿真。

B型火炮摇架与上架、上架与上架底板之间采用耳轴连接，耳轴采用复合连接器模拟，赋予其除转动方向外其余5个方向等效刚度与阻尼；座圈采用复合连接器模拟，赋予其6个方向刚度；高平机采用轴向连接器模拟，赋予其等效刚度，并加载初始平衡力。B型火炮其余部件连接方式与A型火炮相同。选取底凹弹常温全装药在0°方向角/0°射角的射击工况作为计算工况。

火炮下部架体与土壤之间的相互作用关系可通过下部架体与土壤三维模型建立接触和采用集中参数模型两种方案，为提高计算效率，采用质量- 弹簧- 阻尼单元的集中参数模型进行模拟[2]。

下面通过全炮发射动力学仿真，研究缓冲器布置方案对全炮射击稳定性的影响。

2.3 A型火炮后大架缓冲发射动力学分析

本文研究中考察的超轻型火炮射击稳定性限于发射过程前期的火炮结构稳定性，用前大架跳高来表征。首先运用有限元法分别建立A型火炮缓冲器上置(见图15)和缓冲器下置(见图16)的全炮刚柔耦合发射动力学模型，通过发射动力学模型试算对影响跳高的缓冲器弹簧刚度、预压力、阻尼、行程等参量进行优化匹配，然后进行发射动力学仿真分析，计算结果如图17和表3所示。

图15 A型火炮缓冲器上置动力学模型Fig.15 Dynamic model of A-type artillery with buffer on top of backtrail

图16 A型火炮缓冲器下置动力学模型Fig.16 Dynamic model of A-type artillery with buffer underneath backtrail

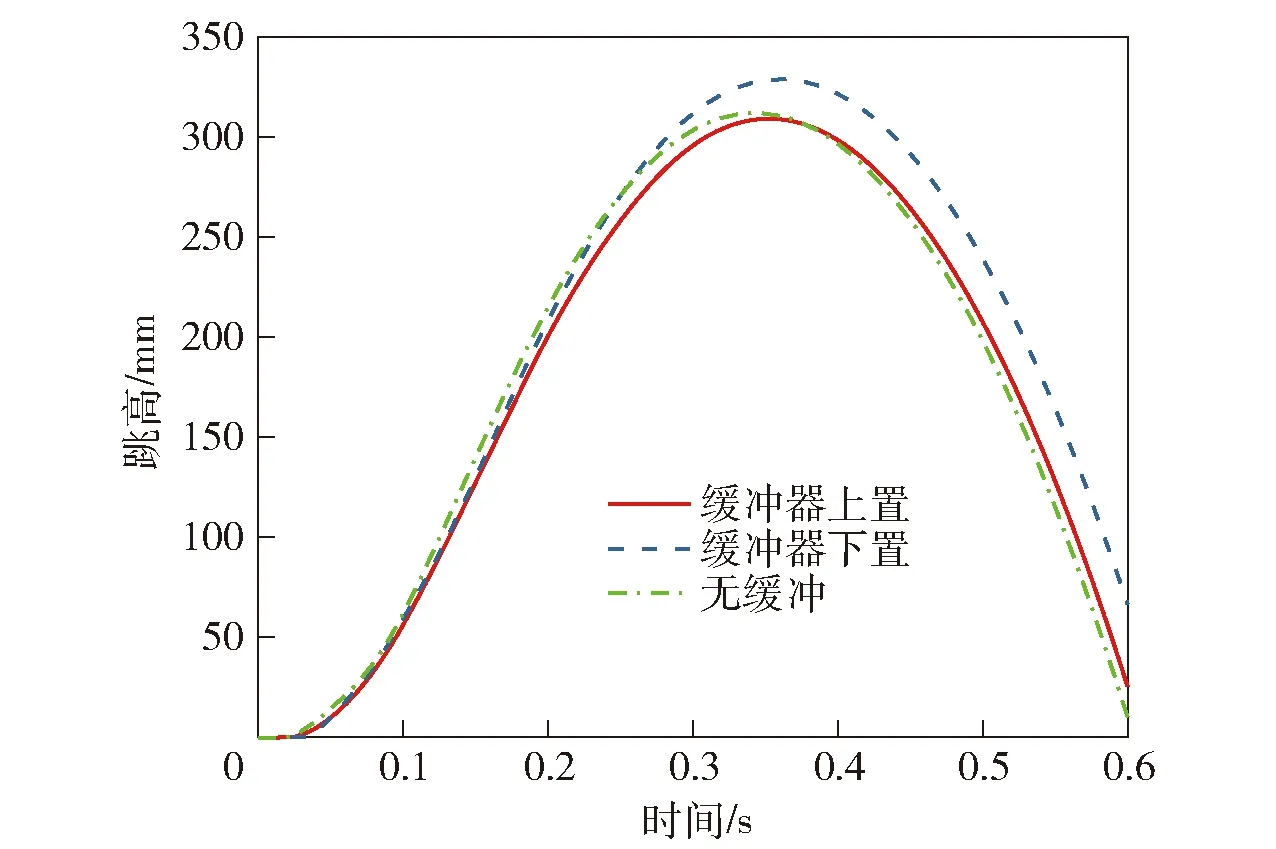
图17 A型火炮前大架跳高Fig.17 High jump of front shelf of A-type artillery

表3 A型火炮前大架跳高Tab.3 High jump of front shelf of A-type artillery mm

上述仿真计算表明，A型火炮射击时前大架跳动量过大，射击稳定性不理想，且采用后大架缓冲不能改善射击稳定性。采用缓冲器下置方案的AH4样机试验，也支持上述计算结果。

2.4 B型火炮后大架缓冲发射动力学分析

建立B型火炮缓冲器上置(见图18)和缓冲器下置(见图19)的全炮刚柔耦合发射动力学模型，通过发射动力学模型试算对影响跳高的刚度、预压力、阻尼、行程等参量进行优化匹配，再进行发射动力学仿真分析，计算结果如图20和表4所示。

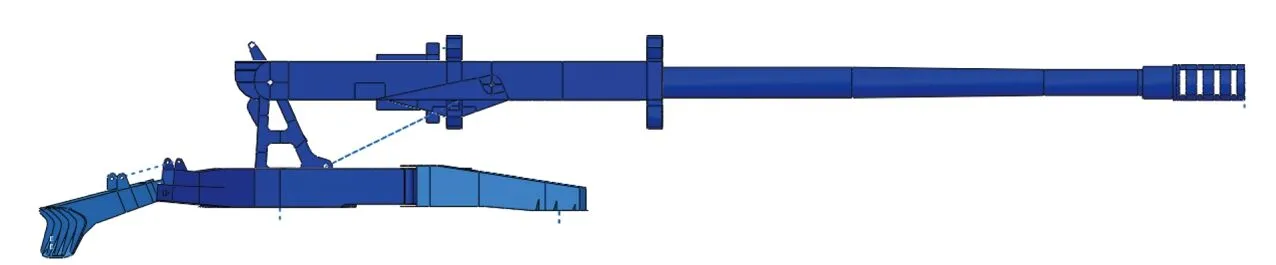
图18 B型火炮缓冲器上置动力学模型Fig.18 Dynamic model of B-type artillery with buffer on top of backtrail

图19 B型火炮缓冲器下置动力学模型Fig.19 Dynamic model of B-type artillery with buffer underneath backtrail

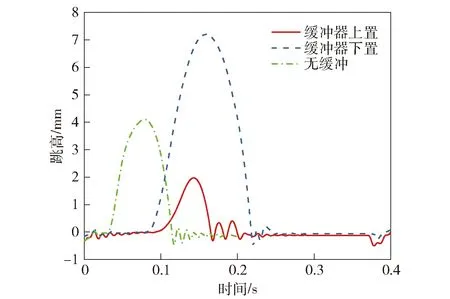
图20 B型火炮前大架跳高Fig.20 High jump of front shelf of B-type artillery

表4 B型火炮前大架跳高Tab.4 High jump of front shell of B-type artillery mm

表4中的计算结果表明，具备某高效射击稳定性控制原理的B型火炮相对于A型火炮前大架跳高大幅度减小，样机试验结果得到了验证。

对比上述计算结果可知，采用无缓冲方案时B型火炮已具备优异的射击稳定性，缓冲器上置的后大架缓冲方案可在一定程度上进一步提高B型火炮的射击稳定性。由于实际使用中不同季节和地点的炮位土壤特性会有非常显著的变化，无缓冲方案的射击试验表明，表4中前大架跳高数值可能有数倍至一个数量级的增加，从而显现了采用后大架缓冲减小跳高的必要性。

3 缓冲器特性优化设计

3.1 参数化有限元模型

第2节发射动力学计算结果表明，采用后大架缓冲不能改善A型火炮射击稳定性，因此本文仅对B型火炮缓冲器上置方案进行发射动力学参数化建模和特性优化研究。

通过优化缓冲器节制杆外形尺寸实现对发射过程缓冲器工作特性的优化设计。优化过程需要参数化全炮刚柔耦合发射动力学模型，实现变化设计变量下火炮及缓冲器动态特性分析。

本文动力学有限元模型的参数化，通过模型中缓冲器特性计算用户子程序读取的节制杆直径参数外部文件在优化循环中变量化实现。

3.2 试验设计及近似模型

为了缩短优化周期，对于复杂的工程问题，通常采用试验设计+近似模型方法将复杂的结构动力学模型转换为数学模型，使单次计算时间大大降低，优化效率大幅度提高。

由于全炮刚柔耦合动力学模型兼具几何非线性、材料非线性、边界条件非线性的特点，采用Kriging模型最为合适。样本点的选取采用最优拉丁超立方(OLHD)的方法。通过试验设计的方法获取200个样本点，对样本点逐一进行有限元计算，由输入输出值建立近似模型，经验证后将近似模型用于寻优计算。近似模型常用的拟合精度评价指标有平均相对误差RAAE、最大相对误差RMAE、均方根误差RSME及决定系数R2.Kring近似模型拟合精度如表5所示。

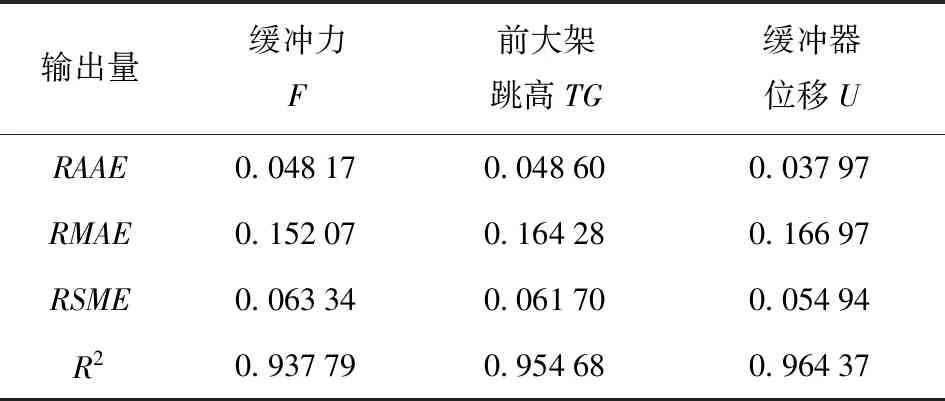
表5 Kriging近似模型拟合精度Tab.5 Fitting accuracy of Kriging approximation model

由表5可以看出，以Kriging近似模型代替全炮刚柔耦合发射动力学模型进行优化计算，具有较高的可信度。

3.3 优化模型的建立

目标函数如下：

(3)

(4)

式中：F0max为原始方案缓冲过程缓冲力最大值；TG0max表示原始方案前大架跳高，以前大架跳高表征火炮的射击稳定性。

建立面向缓冲段缓冲力峰值和射击稳定性的多目标优化模型如下：

minf(f1,f2)，
s.t.dr,min≤dr,i≤dr,max,i=1,2,…,9，
10 mm≤U≤30 mm，
|F|≤100 kN，

(5)

式中：dr,min、dr,max分别为节制杆直径的上限、下限，dr,min=9.0 mm，dr,max=9.9 mm；dr,i为缓冲器节制杆直径。为对缓冲段节制杆参数进行优化，选取缓冲段的7个直径参数作为设计变量。

对建立的近似模型进行寻优计算，该优化是基于Pareto理论的多目标优化问题，选用NSGA-Ⅱ.其流程如图21所示。

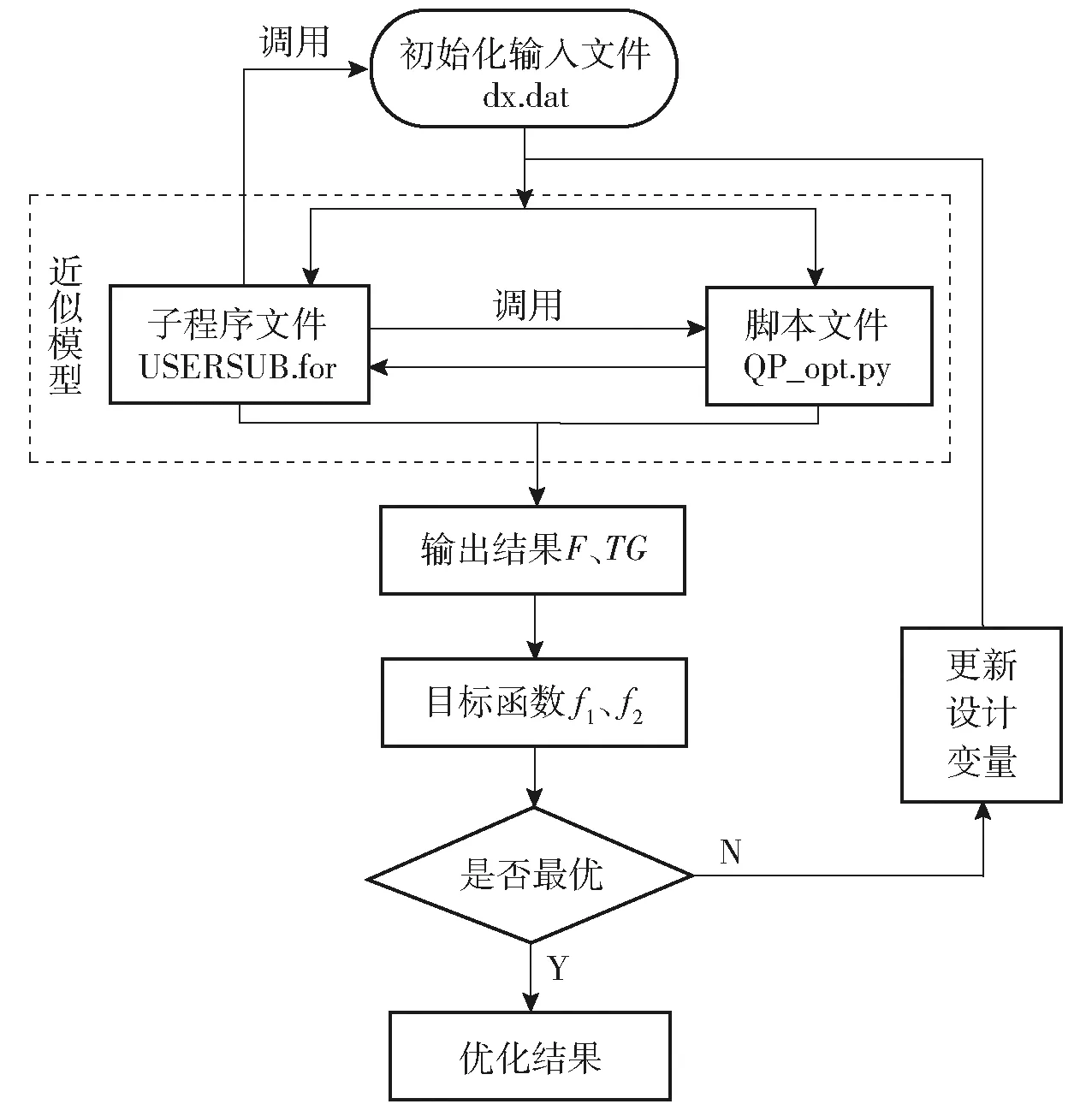
图21 优化流程图Fig.21 Optimization flow chart

为了减小缓冲力峰值及提高火炮射击稳定性，采用NSGA-Ⅱ[6-7]，对缓冲器缓冲段节制杆尺寸参数进行优化，并在3.4节中对优化前后的结果进行对比分析。

3.4 优化结果分析

通过计算得到目标函数f1和f2的Pareto解集，Pareto前沿面如图22所示。选取C点作为模型缓冲过程的优化解，优化前后的节制杆尺寸数据如表6所示。

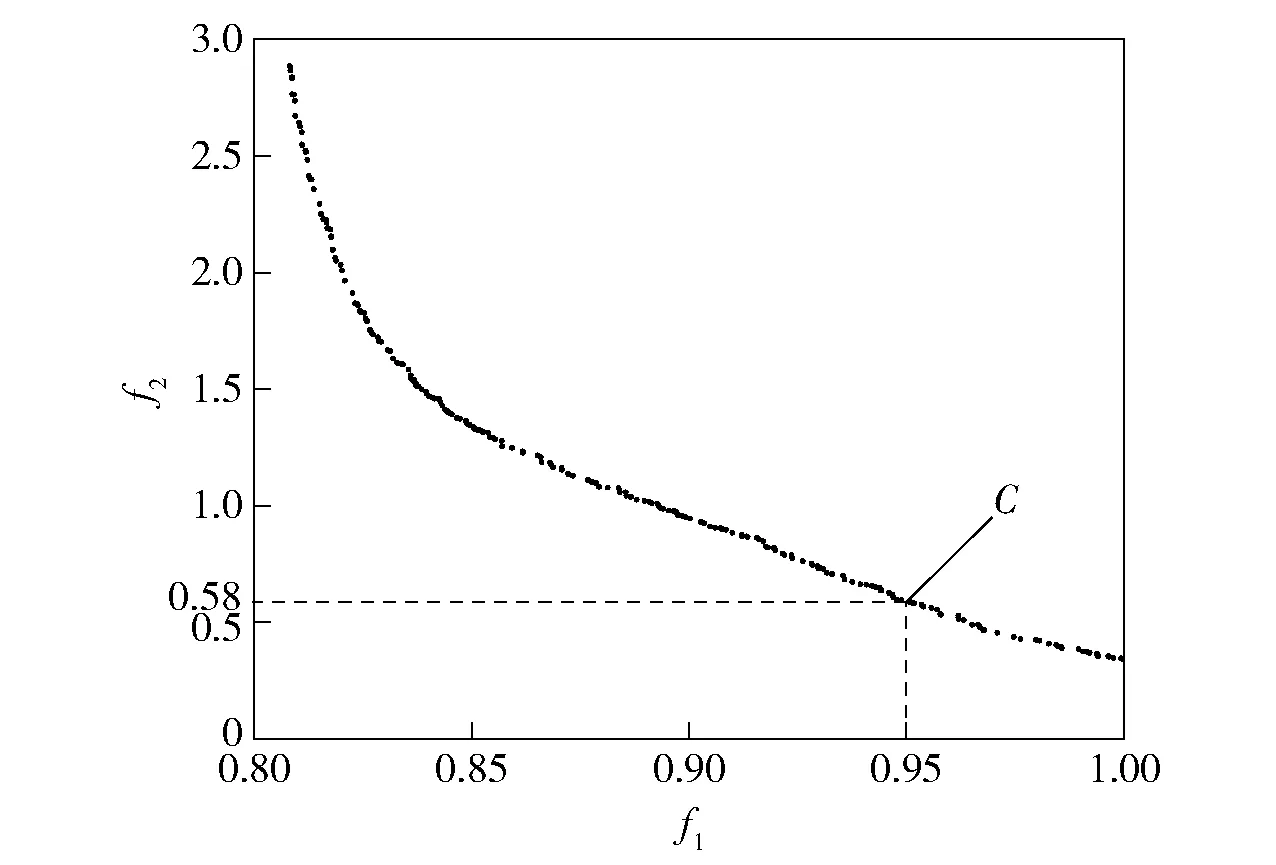
图22 缓冲段f1与f2最优解集Pareto图Fig.22 Pareto diagram of optimal solution set of buffer segments f1 and f2

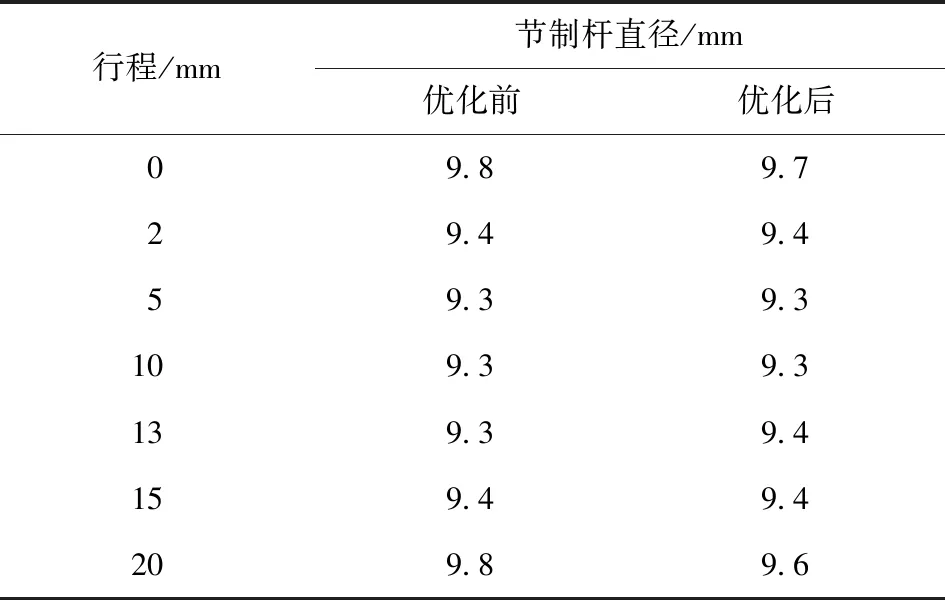
表6 缓冲段的节制杆尺寸前后对比Tab.6 Size comparison of control rod in buffer section

将优化后设计变量代入有动力学有限元模型进行计算，对比动力学有限元模型计算结果与Kriging近似模型计算结果，如表7所示。

表7 动力学有限元模型与近似模型结果对比Tab.7 Comparison of calculated results of dynamic finite element model and approximation model

由表7计算结果可知，动力学有限元模型计算结果与Kriging近似模型计算结果误差在5%以内，表明采用Kriging近似模型代替动力学有限元模型进行优化计算是可行的。

将优化前后的设计变量分别代入动力学有限元模型进行计算，结果如图23～图29所示。表8为初始缓冲特性、优化后缓冲特性。

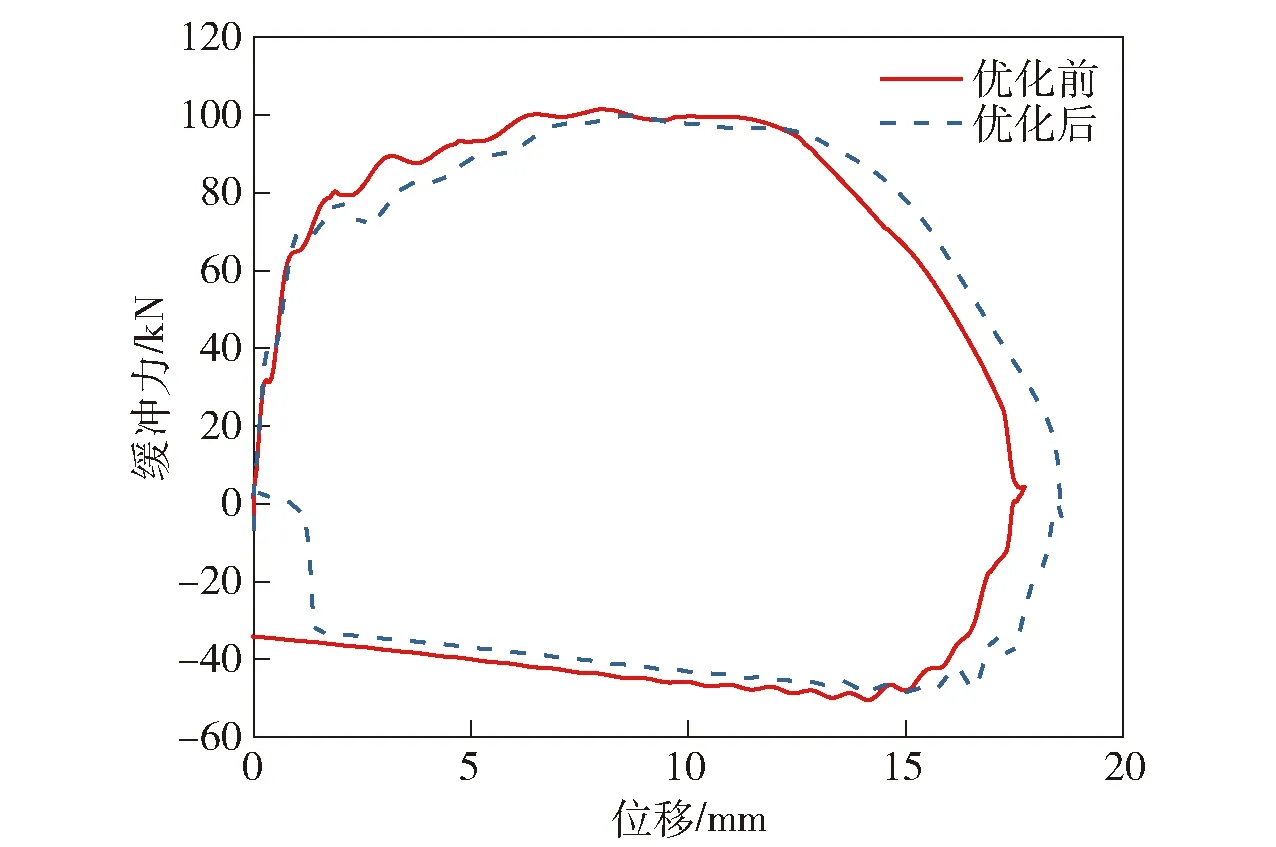
图23 优化前和优化后缓冲力曲线Fig.23 Buffer force curves before and after optimization

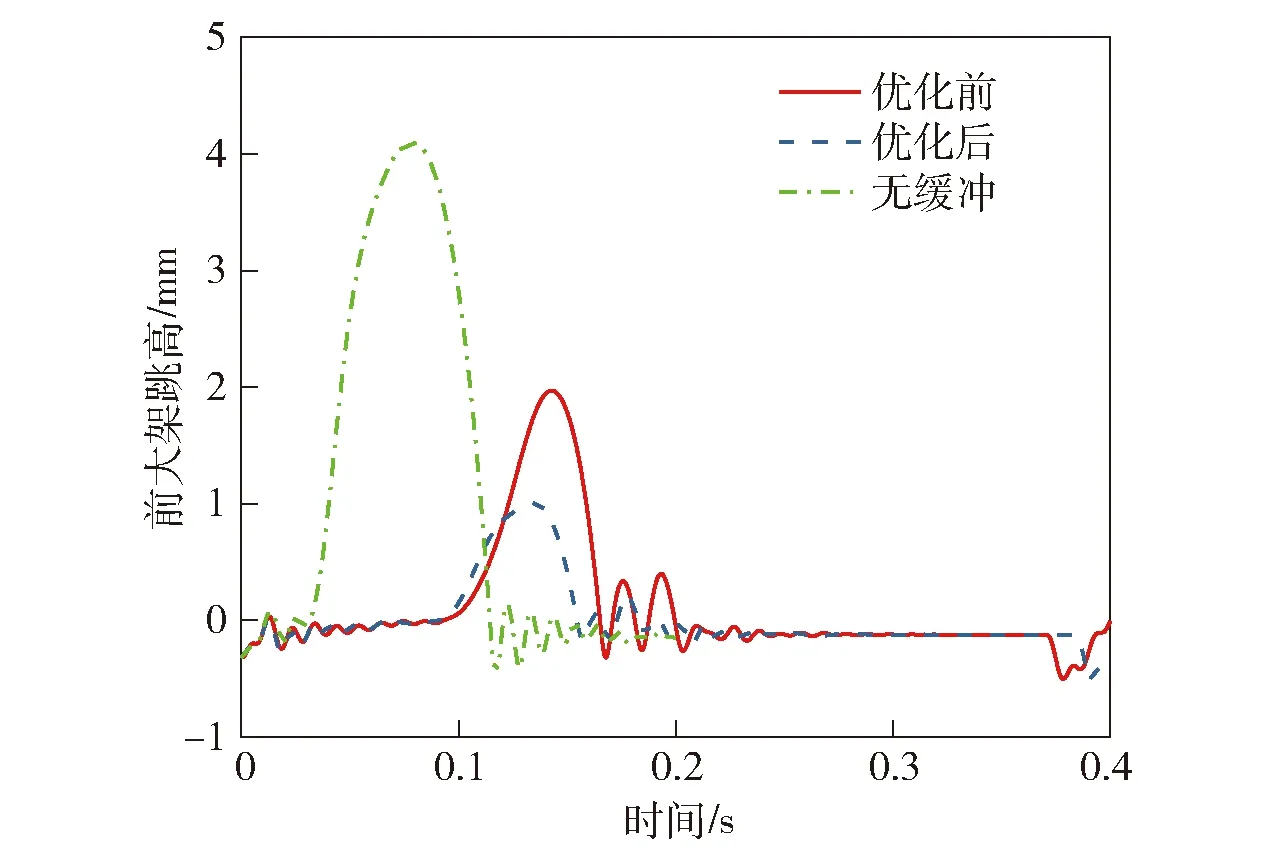
图24 优化前后及无缓冲前大架跳高曲线Fig.24 Pre-optimized,optimized and unbuffered high jump curves

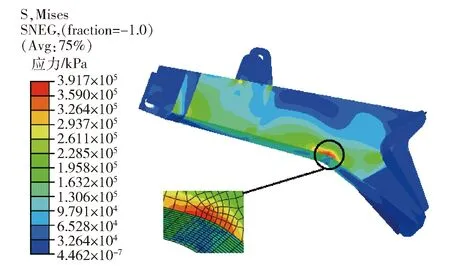
图25 后大架应力云图Fig.25 Stress cloud chart of backtrail

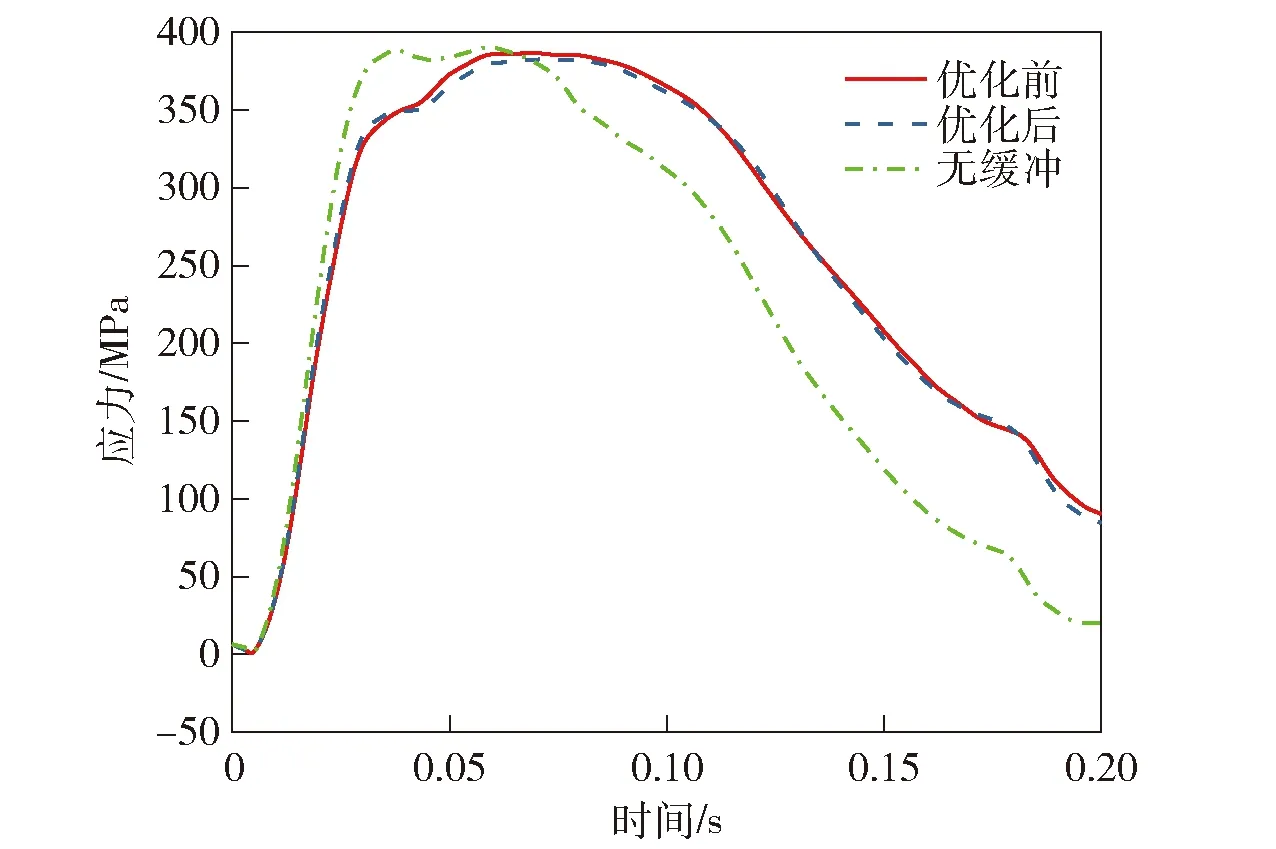
图26 后大架最大应力对比Fig.26 Maximum stress comparison of backtrail

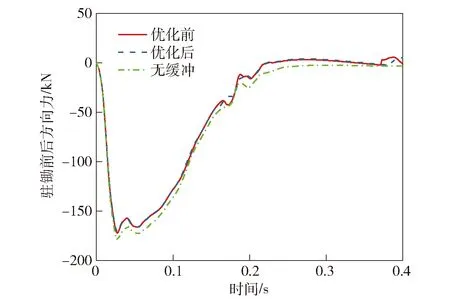
图27 后大架驻锄前后方向力Fig.27 Forces in front and rear directions of standing hoe of backtrail

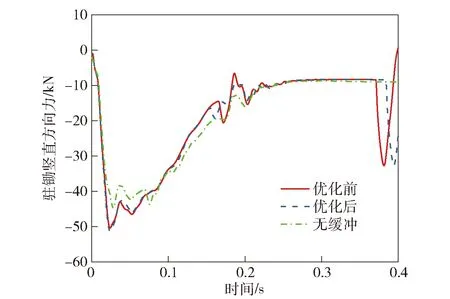
图28 后大架驻锄竖直方向力Fig.28 Forces in vertical direction of standing hoe

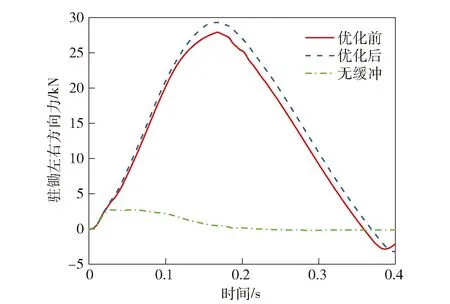
图29 后大架驻锄左右方向力Fig.29 Forces in left and right directions of standing hoe of backtrail

结合图23～图29以及表8可知，在B型火炮缓冲器上置方案基础上，通过对缓冲器缓冲段的节制杆尺寸优化，使得缓冲过程中的缓冲力峰值减小了1.8%，后大架最大应力点处应力减小了1.16%.

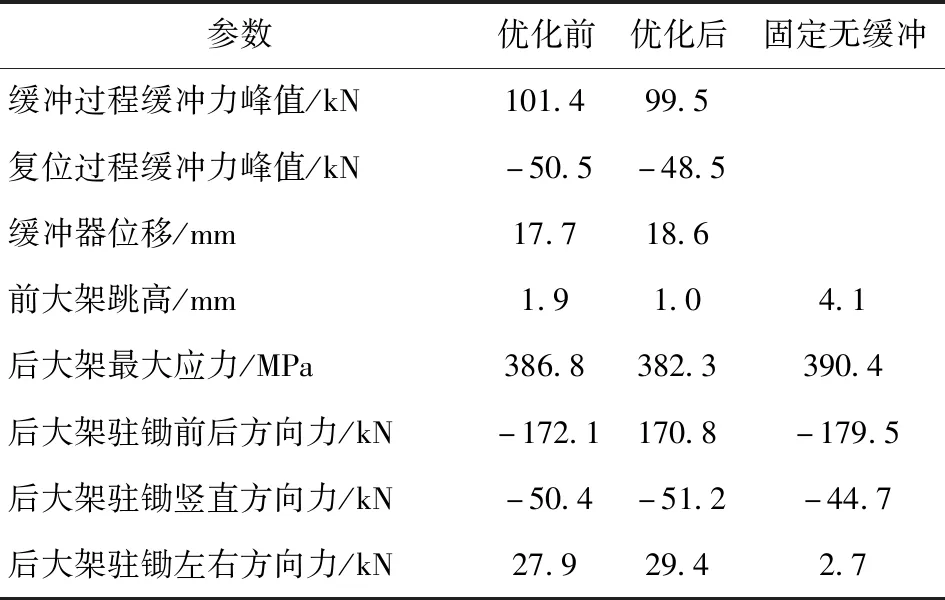
表8 初始缓冲特性、优化后缓冲特性Tab.8 Initial and optimized buffe ring characteristics

4 结论

本文针对某口径两种不同类型超轻型火炮，采用全炮发射动力学刚柔耦合有限元法，对缓冲器上置和下置的后大架缓冲方案对火炮射击稳定性的作用机理和效果进行了分析。研究结果表明：1)后大架缓冲不能改善A型火炮(M777一类结构原理的火炮)的射击稳定性；2)缓冲器上置的后大架缓冲方案可在一定程度上提高B型火炮的射击稳定性，并降低驻锄与后大架本体交接部位的发射应力。

总之，通过本文研究揭示和澄清了超轻型火炮后大架缓冲对火炮射击稳定性的作用。