基于多分辨率复合阵列的未知信源数波达方向估计
(上海无线电设备研究所,上海 201109)
0 引言
多分辨率复合阵列(Multi-Resolution Composite Arrays,MRCA)是由数个阵元间距不同的均匀线性子阵列(Uniform Linear Sub-Arrays,ULSA)组成的非均匀线阵(Non-niform Linear Arrays,NLA)[1-5]。相比于阵元数相同的均匀线阵,多分辨率复合阵列具有更大的有效孔径、更高的测向精度和角度分辨率,因而在波束形成与波达方向(Direction-of-Arrival,DOA)估计领域受到关注[3]。
互质阵列可以看成仅有2 个子阵的多分辨率复合阵列[6-8],即两个子阵的阵元间距均大于半波长。目前基于互质阵的DOA 估计主要利用解模糊的方法进行空间谱估计[9-10]。文献[10]提出了一种联合MUSIC 估计算法,该方法利用互质特性去除子阵DOA 估计存在的角度模糊。由于仅有两个子阵,该算法仅能估计一个不模糊目标信号。在多目标信号情况下,基于解模糊的DOA 估计方法需要通过多分辨率复合阵列实现。
基于解模糊的思想,本文将密集阵的DOA 估计算法拓展至多分辨率复合阵列中,如多重信号分类(Multiple Signal Characterization,MUSIC)算法。然而,这些算法都需要有信源数目作为算法的先验信息,信源数的准确性影响DOA 估计性能。虽然现有文献给出了信源数目估计方法[11-14],但是这些方法无法解决信号相干的问题。为了解决这一问题,文献[15]提出一种基于未知信源数的相干信号DOA 估计方法,但该方法直接运用于多分辨率复合阵列中将导致计算量过大的问题。
本文基于解模糊的思想和文献[15]中的方法,提出了一种改进的基于子阵空间谱联合的DOA 估计算法,该算法将文献[15]中的算法拓展至多分辨率复合阵列的DOA 估计中。通过对各子阵构造一个无需信源数的代价函数,免去信源数先验性信息的需求。考虑到各子阵进行全范围搜索计算量较大,提出了从单个不模糊区搜索,反推全部模糊角度的改进方案,并利用联合代价函数匹配的方法,获得真实的角度估计。该方法有效克服了传统全空间搜索算法需信源数先验性信息的缺点,同时通过不模糊区搜索的方式减少计算量。
1 信号模型
考虑由Q个阵元数为2M+1 的均匀直线阵构成的多分辨复合阵列,子阵的阵元m依次为-M,…,0,…M,其拓扑结构如图1 所示。记第q个子阵的阵元间距为,其中,λ为载频波长,正整数Zq>1,且两两互质。

图1 多分辨复合阵列模型Fig.1 Multi-resolution composite array model
假设存在K(K<Q且K≤M+1)个远场窄带信号,其中前Kc个信号为相干信号,第k个信号的波达方向记为θk(θk∈(-π/2,π/2),k=1,2,…,K)。对于相干信号,记第一个信号为s1(t),则其余相干信号可表示为

第子阵q关于θk的导向矢量为

则第q个子阵接收到的信号可表示为

式中:Nq(t)为均值为0 方差为σ2的高斯白噪声矩阵;Aq为子阵q所有导向矢量构成矩阵;S(t)为所有信号构成的信号矩阵。
2 基于子阵空间谱联合的DOA 估计方法
基于子阵空间谱联合的DOA 估计方法首先对各个子阵进行DOA 估计得到所有的模糊角度,然后利用子阵互质的特性,联合子阵空间谱剔除虚假角度获得真实的DOA 估计。
2.1 托普利兹变换
子阵q的协方差矩阵为

基于信号相关的假设,协方差矩阵Rq中的每一个元素可表示为

式中:


选取协方差矩阵Rq的第m行,构造如下形式的托普利兹矩阵:

2.2 未知信源数的DOA 估计
当子阵q不存在模糊时,即Zq=1,对于子阵q构成的2M+1 个托普利兹矩阵,仅有M+1 个矩阵包含不同的统计信息。由于Sqm为满秩矩阵,因此,可利用这M+1 个托普利兹矩阵进行DOA 估计。在对于第k个信号,总存在矢量bk∈C(M+1)×1,使得bk与剩余K-1 个信号新导向矢量构成的空间相互垂直,可得到

联立式(9)和式(10)可得

根据式(11)可以假设在不考虑噪声的条件下,若真实的波达方向为θk,则存在一个尺度因子gqm使得

再考虑噪声影响,从而有以下优化问题:

由于gq和bk未知,无法通过直接搜索DOA 优化式(13)。因此,需要对式(13)进行简化,基于文献[15]的结论,最终可简化为

通过谱峰搜索的方式即可获得各个子阵的DOA 估计,然而在多分辨率复合阵列中Zq>1,使之存在角度模糊问题。
2.3 子阵空间谱联合
当子阵的阵元间距大于半波长时,即Zq>1 时,通过子阵得到的波达方向估计值有角度模糊。如果真实角度为θ,模糊角度为θa,则两者之间存在如下关系:



联立式(18)和式(19)可得

在多分辨率复合阵列中Zq两两互质,因而不存在k1、k2使得等式(19),即仅有K个真实DOA 可同时为Q个子阵的估计值。如图2 所示,给出了K=2、Q=3 时各子阵的空间谱,其中3 种不同颜色的曲线分别表示3 个子阵全空间搜索得到的空间谱,虚线表示真实波达方向。可看出仅在真实角度的区间内才存在3 个子阵空间谱谱峰的重叠,且谱峰周期性出现,重复次数为Zq。

图2 各子阵的空间谱Fig.2 Spectra of subarrays
而采用MUSIC 算法对3 个子阵全空间搜索时,若信源数估计错误,各子阵的空间谱无法对所有波达方向进行准确估计。此处设置为1,MUSIC 算法各子阵的空间谱如图3 所示。从图3 中可看出,谱峰虽周期性出现,但其重复次数不为Zq,且真实角度的区间内3 个子阵空间谱谱峰并未出现重叠,因此,无法准确估计波达方向。

图3 MUSIC 算法的各子阵空间谱Fig.3 Spectra of subarrays obtained by the MUSIC algorithm
对子阵q在()范围内进行未知信源数的DOA 估计,可得其全部模糊角度,假设为Nq(Nq<Zq⋅K)个。基于上述结论,其中仅有K个DOA 估计值带入其余子阵代价函数和式中取小值,公式为

式中:θqn为子阵q的第n个DOA 估计值。
3 改进的快速DOA 估计方法
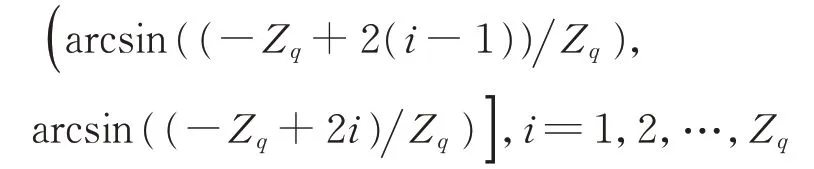
在不模糊区间中进行DOA 估计,仅有与信源数一致的K个波达方向估计值。利用式(16)可推出剩余模糊角度,减少角度搜索范围,从而降低计算量。此外,不模糊区域的角度范围相对于全范围有所缩减,导致部分子阵中模糊角度间距更近。受信噪比和阵元数影响,算法分辨率较低无法将其区分,使得该子阵不模糊区域内的谱峰数目小于信源数K。因而需要剔除谱峰数量较小子阵,避免影响后续匹配。改进后的未知信源数的DOA 估计算法步骤大致如下:
步骤1利用估计子阵的协方差矩阵,L为快拍数。
步骤2选择协方差矩阵的前M+1 行构造如式(9)的托普利兹矩阵。
步骤3选择不模糊区域,计算Fq、Gq(θ),并利用式(15)求解该不模糊区域的空间谱Pq(θ)。
步骤4对Pq(θ)进行谱峰搜索,得到对应的模糊角度,利用式(17)可推出剩余模糊角度。
步骤5选择不模糊区域内谱峰数量最大且相等子阵的模糊角度,利用式(21)获得真实的DOA。
步骤6对各子阵求得DOA 进行排序和平均,得到最终的DOA。
未知信源数DOA 估计单个角度搜索的计算量为O[(2M+1)2N+(M+1)4+5(M+1)3],若假设快拍数为L,在()范围内角度步长为Step 所对应的搜索次数为Nstep,则该算法的计算量接近。由于,因此,改进后算法计算量得到较大的降低。
4 仿真试验及结果分析
本节通过仿真试验验证本文所提算法的性能,同时与采用全空间搜索的多重信号分类算法(TSSMUSIC)和采用全空间搜索的Capon 算法(TSSCapon)进行性能对比。在使用TSS-MUSIC 算法及TSS-Capon 算法时,假设信源数目已知。仿真实验采用多分辨率复合阵列结构,如图1 所示,子阵数Q为4,子阵阵元数2M+1 为9,各子阵的阵元间距依次为,即Z1=2,Z2=3,Z3=5,Z4=7。设置3 个远场窄带信号,其中前2 个为相干信号,DOA 依次为θ1=-5°,θ2=3°,θ3=25°。设置搜索步长为0.05°。
实验一固定快拍数L为300,基于1 000 次独立的蒙特卡洛仿真,给出了DOA 估计值的均方根误差(RMSE)随信噪比(SNR)变化曲线,如图4 所示。由图可知,在SNR 较小时(<0 dB),本文所提出的算法的RMSE 大于其他2 种算法。但当SNR大于6 dB 时,该算法的RMSE 则明显低于其他2 种算法。当SNR 大于15 dB 时,该算法的RMSE 仅为TSS-MUSIC 算法和TSS-Capon 算法1/2。

图4 DOA 估计的均方根误差与SNR 关系Fig.4 Relation between the RMSE estimated by the DOA and the SNR
实验二固定快拍数L为300,基于1 000 次独立的蒙特卡洛仿真,以搜索步长的一半,即0.025°作为DOA 估计的分辨成功率,给出了DOA 估计的分辨成功率(Success Rate)随信噪比(SNR)变化曲线,如图5 所示。由图5 可以看出,本文提出的算法在SNR 为-5 dB 到0 dB 时,分辨成功率均较低,当SNR 大于0 dB 时,则分辨成功率均快速提高。在分辨成功率为98%时,相比于TSS-Capon 算法,本文提出的算法SNR 改善了5 dB 以上。虽然相对于TSS-MUSIC 算法SNR 无改善,但需注意的是,TSS-MUSIC 算法是在信源数目估计正确的情况下达到98%的分辨成功率,而本文提出的算法无需信源数目先验信息。
实验三固定SNR 为10 dB,快拍数L=[40,60,80,100,150,200,30,500,900],基于1 000 次独立的蒙特卡洛仿真,给出DOA 估计值的均方根误差(RMSE)随快拍数变化,如图6 所示。由图6 可看出,快拍数L<60 时,本文所提出算法的RMSE 大于其他2 种算法,但随着快拍数的增加该算法的RMSE 逐渐降低,而TSS-Capon 算法和TSS-MUSIC 算法则没有明显改善。当L>150 时,本文提出算法的RMSE 明显低于其他2 种算法。

图5 DOA 估计的分辨成功率与SNR 关系Fig.5 Relation between the success rate estimated by the DOA and the SNR
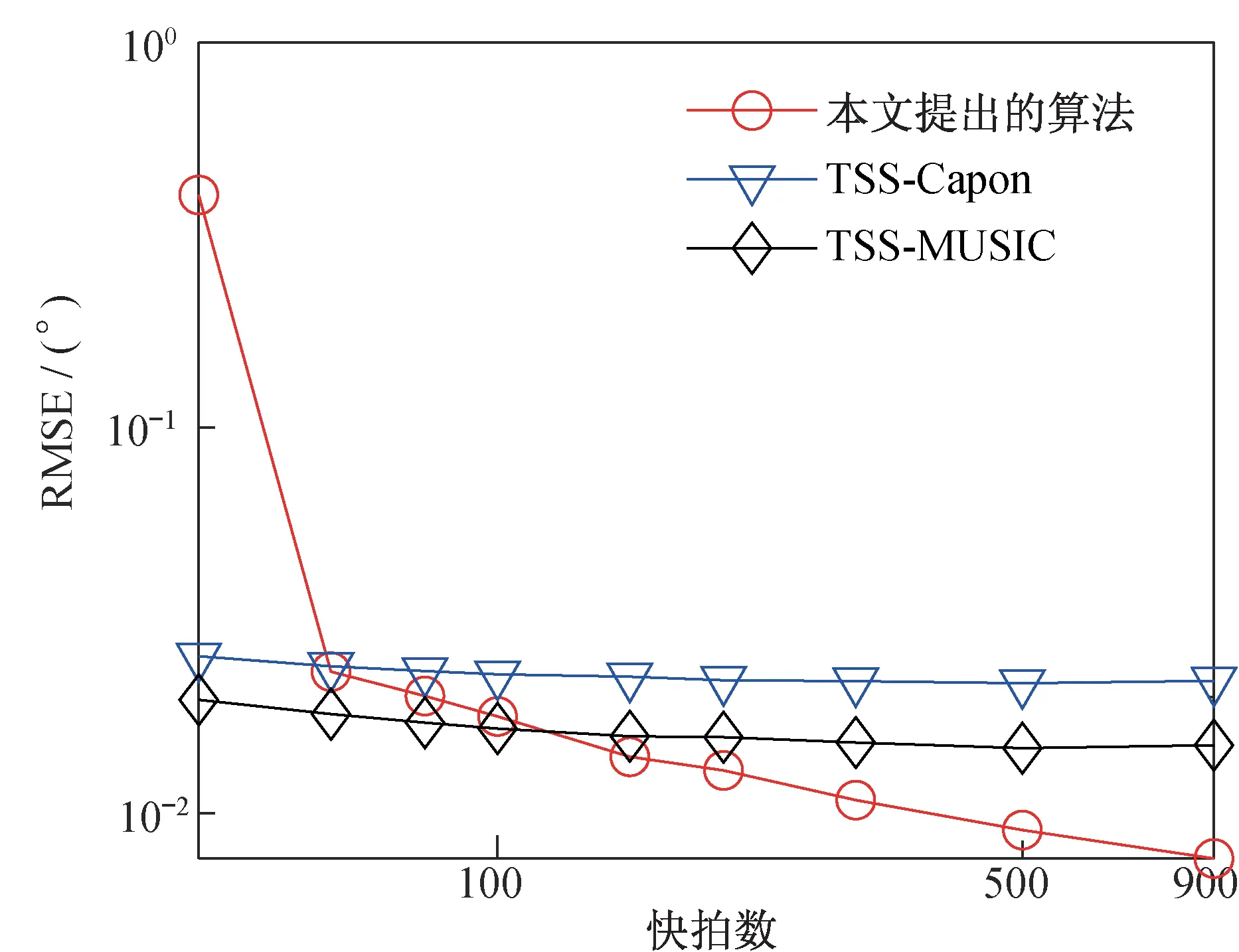
图6 DOA 估计的均方根误差与快拍数关系Fig.6 Relation between the RMSE estimated by the DOA and the number of snapshots
实验四固定SNR 为10 dB,快拍数L=[40,60,80,100,150,200,30,500,900],基于1 000 次独立的蒙特卡洛仿真,以搜索步长的一半,即0.025°作为DOA 估计的分辨成功率,给出了DOA 估计的分辨成功率随快拍数变化曲线,如图7 所示。由图7可以看出,TSS-Capon 算法的DOA 估计的分辨成功率均变化平缓,并逐渐趋于72.4%,而本文提出的算法和TSS-MUSIC 的DOA 估计的分辨成功率均则随着快拍数的增加快速提高,当快拍数L为300时,2 种算法的分辨成功率达到99.2%。

图7 DOA 估计的分辨成功率与快拍数关系Fig.7 Success rate of DOA estimation versus snapshots
从仿真结果可以看出,在高信噪比、多快拍数的条件下,本文所提出的算法DOA 估计精度优于TSS-MUSIC 算法和TSS-Capon 算法。而在信噪比较低、快拍数较少的条件下,本文所提出的算法DOA 估计略差于TSS-MUSIC 算法和TSS-Capon算法。这是由于未知信源数相干信号DOA 估计算法在信噪比较低、快拍数较少时分辨率较低,导致部分子阵列DOA 估计中无法区分两相邻信号,在步骤5 被剔除,信息未被使用,因而性能受到影响。
5 结束语
本文研究了基于多分辨率复合阵的未知信源数相干信号DOA 估计问题。将未知信源数相干信号DOA 估计方法扩展至多分辨率复合阵列中,针对多分辨率复合阵列的信号特点,通过各子阵的不模糊区间搜索,反推其余模糊角度的方式减少计算量,并利用利用匹配的方式实现未知信源数DOA估计。仿真结果表明,在高信噪比、多快拍数的条件下,本文所提出的算法DOA 估计精度优于TSSMUSIC 算法和TSS-Capon 算法。后续可尝试利用求根公式替代空间搜索,从而进一步减少计算量。

