画图——低段学生解决问题的“脚手架”

苏浙闽

【摘要】纵观学生解决问题的情况，画图能力的缺失实在令人担忧。特别是低段学生本身的识宁量不多、理解能力较弱，对于解决问题就难上加难。我们需要充分地利用教材，从低年级开始，有计划地教给学生一些画图能力，从“扶”到“放”，最后让学生学习“线段图”，逐步培养学生的画图能力，从而给他们一个解决问题的“脚手架”。

【关键词】低段学生;解决问题;画图

中图分类号：G623

文献标识码：A

文章编号：0493-2099（2020）30-0141-02

Drawing-"Scaffolding" for Low-level Students to Solve Problems

（Taishun County Experimental Primary School， Zhejiang Province，China） SU Zhemin

【Abstract】Looking at how students solve problems， the lack of drawing skills is really worrying. Especially the low-lev-el students' own literacy and comprehension ability are weak， which makes it more difficult to solve problems. We need tomake full use of textbooks， starting from the lower grades， to teach students some drawing skills in a planned way， from "sup-porting" to "releasing" and finally letting students leam "line segment diagrams"， gradually cultivate students' drawing skills，and give them a "Scaffolding" to solve the problem.

【Keywords】Low-level students; Problem solving; Drawing

一、适时渗透——仿

（一）渗透画图

低段学生的动手操作非常重要，但是学生在多次动手摆的过程中往往容易受学具的诱惑，而直接影响学生听课和思考的效果，我们有必要让学生用“画”来代替“摆”。王永老师在《情境教学不可忽视“去情境化”问题》一文中提到：北师大版教材怎么上加法的起始课？（1）看笑笑一只手拿着几支铅笔，就在本子上画几个网圈。（2）再看笑笑另一只手拿着几支铅笔，继续画几个网圈。这时学生都画出了如下的图：? ? ? ? ?（3）数一数，一共画了几个圈？（4）想一想，你所画的几个圈表示什么意义？

通过以上的操作与思考活动，每个学生都会发现一个数学事实，即2支铅笔与3支铅笔合起来是5支铅笔。在解决问题中，教师告诉学生可以用数学符号记录所发现的数学事实：3+2=5。我们可以用这种方法让学生在计算时都模仿地画一画，真正理解加法的含义。

（二）突出优势

在学生碰到数学信息比较模糊的时候，让学生有画图的需要。比如：我前面有9人，后面有5人，求一共有多少人？，学生异口同声地回答：9+5=14，这时教师要有意识地培养学生边读题边画图，显示出画图的优势，引导学生用口表示说话的人，前面有9人，用?????????来代替，后面有5人，用5个圆形?????来代替，学生只要一画出这个图，马上就知道应该是9+1+5=15（人），让学生感受到原来通过画图，可以方便解决问题，让学生慢慢地爱上画图，当学生碰到类似的题目时也能模仿着画和思考。本来是一道非常复杂、难懂的思考题，有了画图的经历，学生理解起来也不费劲。画图在这个问题的解决中起到了“脚手架”的作用。

二、顺藤摸瓜——练

学生在读题时，能一下子报出答案，但是要说想法时却什么也说不出来，据我观察发现学生是凭着生活经验算出得数，而脑中根本就没有一个知识系统，知识是零散的。

如加减混合：“车上原来有67人，到了光明站有25人下车，28人上车，现在有多少人？”学生用生活经验能理解加上上车的人数，减去下车的人数，等于最后的人数，这样的计算在本题中是完全正确的，上课时仅仅满足于此，学生就会形成思维定式，以后碰到“上车”就用加法，看到“下车”就用减法。有了这根“藤”，我们顺“藤”摸“瓜”，要求学生用图表示出想法。让学生真正理解加减混合的真正含义。

方法一（师生一起完成）

教师画原来的人数：

再画下车的人数之后：

（涂色部分是下车的人数）

算：下车后车上还有多少人：67-25=42（人）

教师最后画出上车之后：

（黑色部分用课件覆盖上面的灰色部分）列出算式：42+28=70（人）

方法二：如果先算“上车”的总人数，最后再算“下车”的人数，应该怎么㈣呢？（学生独立完成）

原来的人数：

加上上车的人数：

画出下车的人数：

（黑色表示下车的人数）

学生在方法一的启发下能用图来说明想法，其实才真正懂了。

正如吴正宪老师在教学“猴弟弟摘了4个桃子，猴哥哥比猴弟弟多摘了3个，他们俩一共摘了几个桃子”之前，出示了一道一步计算的题目：猴哥哥摘了4个桃子，猴弟弟摘了3个桃子，他们一共摘了几个桃子？教师画：哥哥?，弟弟?，用大括号连着。在解决两步计算时，要求学生用画图表示出你的想法。学生画出了类似以下的图，经过学生的解释，全班学生一致认为先算猴哥哥摘了4+3=7（个），再算他们一共摘了7+4=11（个）。吴老师用画图的方法突破了本题的难点，为解决稍复杂的数学问题做好了准备。

三、画出精彩——创

如：求一个数是另一个数的几倍。

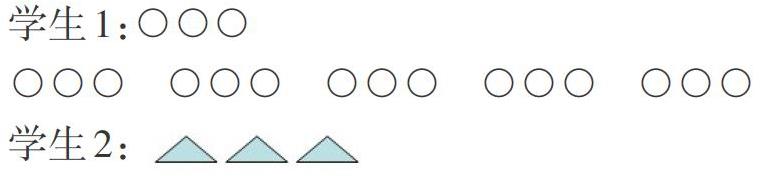
教师出示了3朵黄花，6朵红花，让学生用学具摆一摆说明6是3的2倍。在学生能理解2倍后，教师马上把红花的数量增加到15朵，要求学生用最简单的图形、最快的速度表示出想法。

学生1：???

??? ??? ??? ??? ???

学生2：△△△??? ??? ??? ??? ???

学生能画出简单的图，理解了15里面有5个3，15是3的5倍。

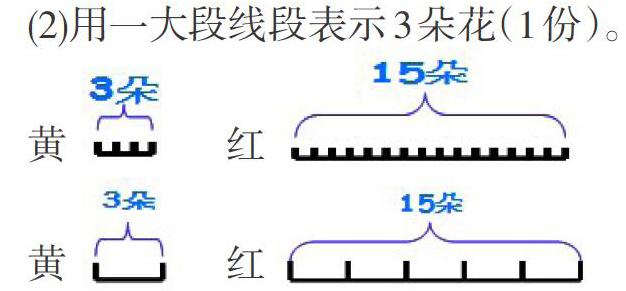
教师补充由花朵演变成线段图的整个过程。在原本会画“一对一”的图，慢慢过渡到“以一代多”的线段图，有必要让学生在二年级开始接触，当真正要用到“以一代多”时才不显得突兀和难以接受。

（1）用一小段线段表示一朵花;

（2）用一大段线段表示3朵花（1份）。

传统应用题教学定式：呈现问题（文字表征）、画线段图（形象表征）、列出算式（数学表征）。我们担心这样教学不利于学生的解决问题能力以及数学思维能力的发展，但另一方面，大家对线段图的价值有着共同的认识：线段图可以更清楚地反映出数量关系，还能培养学生抽象、概括的能力，所以我们需要追寻“继承与创新的和谐”。在低年级，教师应是线段图构造的先行者、示范者、指导者，利用图的形象性帮助学生理解抽象的数量关系。在恰当的时候科学地引入线段图是必要的，学生感受到数学的简洁和奇妙，在以后再用线段图表示题意时，学生觉得很轻松。同时教师需要理解画图的目的是帮助学生分析问题、理解问题，学生会借助白己的经验进行选择，不必为了教线段图而画线段图。

综上所述，画图在低段学生理解问题中确实起到举足轻重的作用，学生在碰到难题时，有意识地在纸上画一画，在脑中绘一绘，把文字转化成图形，就会有新的理解和感悟。画图对学生来说是“我画因我需”，而对于教师则应是“生需故我画”，有计划地教给学生一些画图方法，学生就能拥有终身受用的画图本领，从而给他们一个解决问题的“脚手架”，这对学生学习数学的影响是深远的、有意义的。

参考文献：

[1]于蓉.对第一学段解决实际问题教学的思考[J].小学教学参考，2011（01）.

（责任编辑 李芳）