素养为本 能力为先 突破计算———简析2020年高考化学计算题

◇ 山东 董 军（正高级教师）

1 化学计算是现代化学的三大支柱之一

现代化学的三大支柱是化学理论、化学实验和化学计算．化学理论是化学的核心和灵魂，化学实验是化学研究的基本方式、方法，而现代的化学计算已经超出化学应用的范畴，逐步成为研究化学的一种重要方式、方法．

高考命题，在体现学科核心素养方面探索创新，在考查关键能力方面推陈出新，既在衬托化学概念和化学理论的考查方面增光添彩，又在考查化学计算基本技能和思维能力方面浓墨重彩，使化学计算题在高考中常考常新、百花齐放、精彩纷呈．

2 化学计算是高考永恒的主题，并推陈出新

类型1：“守恒”是“永恒”的主题

化学因其学科特点，“守恒”成为“永恒”的主题，年年必考．由于化学反应的涉及面广，所以，“守恒”在很多方面都有表现，而往往被淹没在具体的知识中．这就要求学生在学习过程中要非常清晰地辨别所学知识块中是否含有“守恒”关系，如质量守恒、原子守恒、能量守恒、得失电子守恒、化合价升降守恒、电中性原理等，要明确其“守恒”的计算原理，这样才能在形式多样的计算题中找到应用“守恒”计算的突破口．

例1（2020年全国卷Ⅲ，节选）一种高性能的碱性硼化钒（VB2）—空气电池如图1所示，其中在VB2电极上发生的反应:

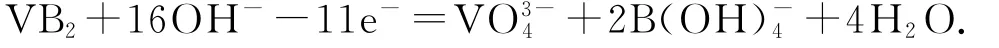
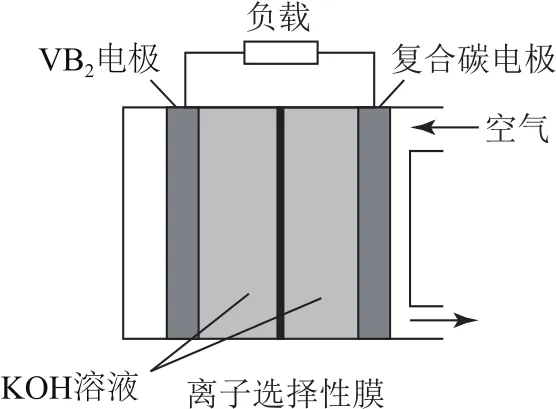
图1

A．负载通过0.04mol电子时，有0.224L（标准状况）O2参与反应

解析

本题的解题依据是得失电子守恒．

① 正解:题给电极反应为失电子反应，可知VB2电极是负极，该电极反应中并没有O2参与反应，则O2必在复合碳电极上参与反应，并且得到电子；根据电解质是KOH溶液，则可推出正极的电极反应为O2＋4 e－＋2 H2O＝4 OH－，计算可知反应有0.224L（标准状况）O2产生．

②简解:一般情况下，1 molO2参与反应得4 mol电子，特殊情况（只有产生H2O2或Na2O2）时得2mol电子，本题中没有信息说明有这两种物质生成，即可直接按得4mol电子计算．

例2（2020年全国卷Ⅰ，节选）为验证不同化合价铁的氧化还原能力，利用图2电池装置进行实验．电池反应一段时间后，测得铁电极溶液中c（Fe2＋）增加了0.02mol·L－1．石墨电极上未见Fe析出．可知，石墨电极溶液中c（Fe2＋）＝________．

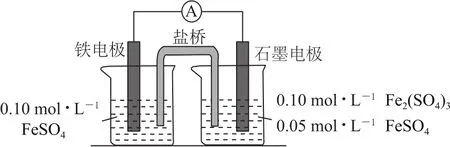
图2

解析

本题解题依据是得失电子守恒，再根据Fe与Fe3＋转化为Fe2＋时电子转移量为2∶1，即可得出答案．详解如下:铁电极反应为Fe－2 e－＝Fe2＋，则溶液中c（Fe2＋）增加了0.02mol·L－1，而石墨电极反应为2 Fe3＋＋2 e－＝2 Fe2＋，溶液中c（Fe2＋）必然增加0.04mol·L－1，故石墨电极溶液中c（Fe2＋）＝0.05mol·L－1＋0.04mol·L－1＝0.09mol·L－1．

例3（2020年全国卷Ⅰ，改编）在Li0.8125Fe PO4中，n（Fe2＋）∶n（Fe3＋）＝________．

解析

本题解题依据是电中性原理．该原理可表述为:化合物保持电中性，或在化合物中正负化合价的代数合为零，或在化合物中正化合价的绝对值之和等于负化合价的绝对值之和．

设在Li0.8125Fe PO4中，Fe2＋和Fe3＋数目分别为x和y，则分别从铁离子数和化合价两个角度列方程组:①x＋y＝1，②0．8125＋2x＋3y＝3，解得x＝0.8125，y＝0.1875，则

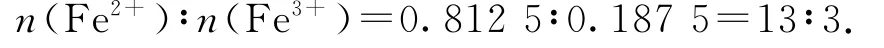
说明例1和例2共同的特点就是已知在电池的一个极上发生了被描述的反应，而要计算另一个电极上相关的物质及其变化，这其中就是“得失电子守恒”成了桥梁．而例3涉及分子式，因此“电中性原理”则成为遵循的法则（在溶液中也是如此）．

点评

“守恒”大家都知道，但很多学生在考场上找不到“守恒”．因此，在学习过程中学生一定要有“守恒”意识，在学习时要挖掘“守恒”，在复习时要总结“守恒”，在笔记中要突出“守恒”，在解题时要应用“守恒”．只有认识到“守恒”的重要性，切实建立了“守恒”意识，在思想上和实际中不断应用“守恒”，才能练就一双捕捉“守恒”的锐眼，才能在高考中找到“守恒”．

类型2：“转化”是老知识、新要求

“物质的转化”一词在化学学科建立之初就已经存在，并且一直贯穿于学科知识及教学的始终，各类化学方程式就是最基本、最好的例证．随着科学技术的发展，随着化学对社会的贡献和价值越来越被高度认可，因此被称为“最具应用性的学科”．在新课标中，对化学的概念进行了修正，把“转化”融入其中．这一重大修改，必将在今后的高考中彰显“转化”的价值．

例4（2020年全国卷Ⅱ，节选）CH4和CO2都是比较稳定的分子，科学家利用电化学装置实现两种分子的耦合转化，其原理如图3所示．若生成的乙烯和乙烷的体积比为2∶1，则消耗的CH4和CO2体积比为________．

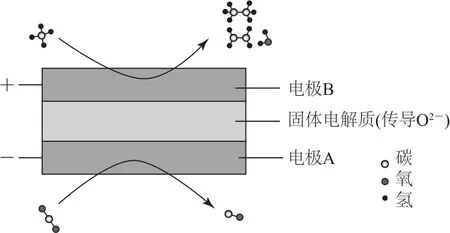
图3

解析

CH4与CO2的反应是学生未知的内容，但物质转化的最准确和最全面的表达方式就是化学方程式．书写化学方程式时一是要求各类物质要全，二是计量数要准确．本题涉及产物可以从图中找到:CH4＋CO2→C2H4＋C2H6＋H2O＋CO，计量数在题中已告知“乙烯和乙烷的体积比为2∶1”，剩下的问题就是方程式的配平了:6 CH4＋5 CO2⇌2 C2H4＋C2H6＋5 H2O＋5 CO，故答案为6∶5．

例5（2020年全国卷Ⅱ，节选）一种有效成分为 Na Cl O2、Na HSO4、Na HCO3的“二氧化氯泡腾片”，能快速溶于水，逸出大量气泡，得到Cl O2溶液．上述过程中，生成Cl O2的反应属于歧化反应，每生成1molCl O2消耗Na Cl O2为________mol．

解析

本题涉及的反应也是学生不知道的内容，所以，分析问题的思路也都是如何建立化学方程式．由于反应体系中物质多（Na Cl O2、Na HSO4、Na HCO3）而生成物只知1种（Cl O2），所以，化学方程式只能写成离子方程式．再根据题给信息“生成Cl O2的反应属于歧化反应”，可在反应物中配上还原剂Cl－，书写时按一般原理“加H除O成H2O”，即得:Cl O－2＋Cl－＋H＋→Cl2↑＋H2O，剩下的就是普通、并不复杂的氧化还原反应方程式的配平了:5 Cl O－2＋4 H＋＝4 Cl O2＋Cl－＋2 H2O，答案显而易见，即1.25mol．

说明这两道例题属于新情境、新素材、新反应，学生第一次见到，不容易理出头绪．例4用文字和图示告诉了反应物和生成物，并且确定了生成物的体积比，据此就能写出化学方程式（6 CH4＋5 CO2＝2 C2H4＋C2H6＋5 H2O＋5 CO）．而例5的题干中告诉了部分反应物和生成物（生成Cl O2的反应属于歧化反应），则可写成离子方程式（5 Cl O－2＋4 H＋＝4 Cl O2＋Cl－＋2 H2O），由方程式计算即可得到答案．

点评

“新信息方程式的书写”是高考的必考项，因为方程式的书写既是必备知识，也是基本技能，更是守恒思想的应用．虽然从初中开始就学习根据化学方程式的计算，但在高考中很多学生往往关注技巧方法，而忘记了用化学方程式这个最根本的依据，这也与学生平时习惯总结用哪些规律和方法来简化计算有直接关系．学习应建立“底线思维”，根据化学方程式的计算是化学计算的万能钥匙、最后一招、镇宅之宝．“新信息方程式的书写”成为高考的必考项，因为它不仅考查必备知识，具有计算功能，还集多项关键能力于一身:有信息，就涉及“接受、吸收、整合化学信息的能力”；不完全的信息，就凸显了“分析问题和解决（解答）化学问题的能力”．在解决问题中，“理解与辨析能力”“分析与推测能力”“归纳与论证能力”和“探究与创新能力”都发挥得淋漓尽致．所以，“新信息、新情境方程式的书写”是一个永恒的话题，是中学教与学的必备形式，要经常练习才能在应用“必备知识”解决具体问题的同时，练就并形成“关键能力”，从而洞察问题的本质并予以科学有效的表示和解决．

类型3：常规计算、深度思维

有人会问:高考试题形式多样，为什么还保留常规计算．笔者认为:它是对重要理论深化理解的必备程序，是发展思维能力、提升思维品质的磨刀石，是培养学生科学态度的好素材，是引导教学的好方法．

例6（2020年全国卷Ⅰ，节选）将组成（物质的量分数）为2m%SO2（g）、m%O2（g）和q%N2（g）的气体通入反应器，在温度t、压强p条件下进行反应．平衡时，若SO2转化率为α，则SO3压强为________，平衡常数Kp＝________（以分压表示）．

解析

本题很明显需要用“三量法”和K的表达式来计算．由于试题中给出的是“物质的量分数”，为解题方便可设:原气体的物质的量为100m o l，则其中SO2、O2和N2的物质的量分别为2mm o l、mm o l和qm o l．则有下列关系:

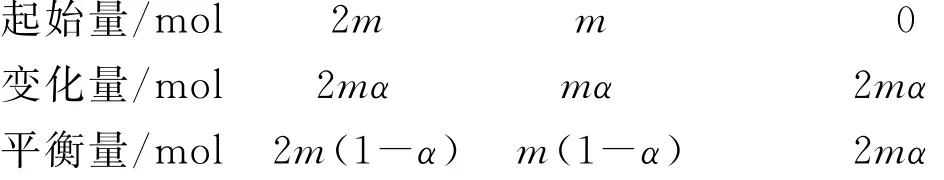
平衡时气体的总物质的量n（总）＝2m（1－α）mo l＋m（1－α）m o l＋2m αm o l＋qm o l，则SO3的物质的量分数为

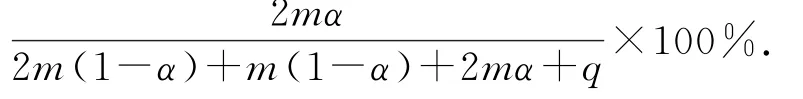
该反应在恒压容器中进行，因此，

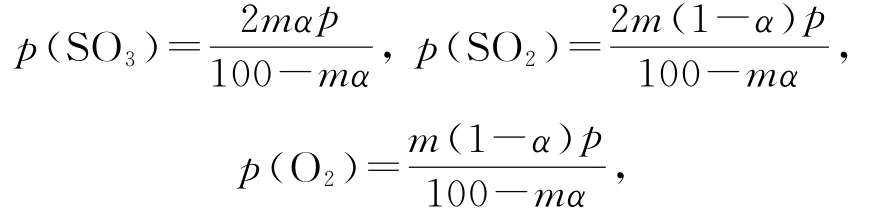
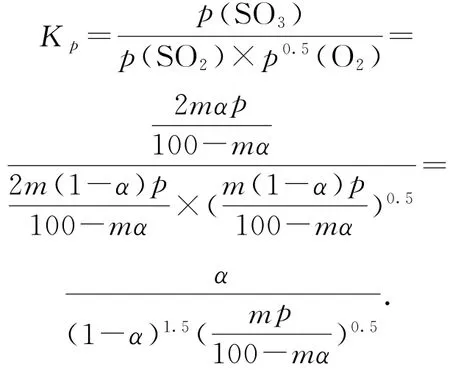
例7（2020年全国卷Ⅱ，节选）乙烷在一定条件可发生如下反应:C2H6（g）＝C2H4（g）＋H2（g）ΔH，相关物质的燃烧热数据如表1所示．

表1

（2）容器中通入等物质的量的乙烷和氢气，在等压（p）下发生上述反应，乙烷的平衡转化率为α．反应的平衡常数Kp＝________（用平衡分压代替平衡浓度计算）．

解析

（1）明显是盖斯定律的常规计算，其过程就是依据信息写出三种物质燃烧的热化学方程式，再整合成试题的要求．

由表中燃烧热数值可知:

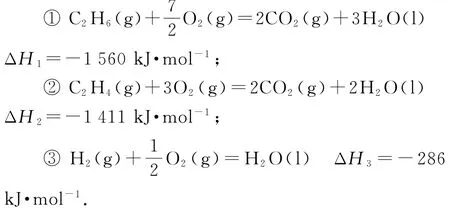
根据盖斯定律可知，①－②－③得:C2H6（g）＝C2H4（g）＋H2（g），则

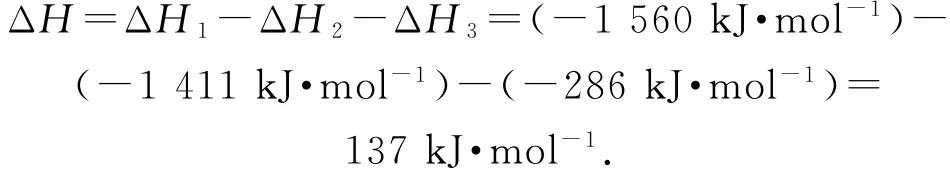
（2）同例6，很明显需要用“三量法”和K的表达式来计算．设起始时加入的乙烷和氢气的物质的量均为1m o l，则有

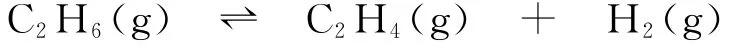
可得平衡时混合物的总物质的量为（2＋α）m o l，则C2H6、C2H4和H2平衡分压分别为和，则反应的平衡常数为

例8（2020年山东卷，节选）探究CH3OH合成反应化学平衡的影响因素，有利于提高CH3OH的产率．以CO2、H2为原料合成CH3OH涉及的主要反应如下:

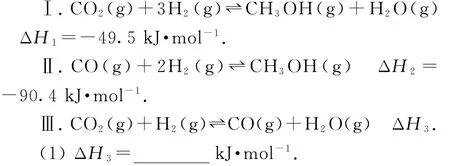
（2）一定条件下，向体积为VL的恒容密闭容器中通入1m o lCO2和3m o lH2发生上述反应，达到平衡时，容器中CH3OH（g）为am o l，CO（g）为bm o l，此时H2O（g）的浓度为m o l·L－1，（用含a、b、V的代数式表示，下同）反应Ⅲ的平衡常数为_______．

解析

（1）是盖斯定律的计算:由反应Ⅰ－Ⅱ＝Ⅲ，得ΔH3＝ΔH1－ΔH2＝－49.5k J·mol－1－（－90.4k J·mol－1）＝＋40.9k J·mol－1；

（2）是多反应的混合计算，理论上难度并不高，但关键在于头脑要清楚、理顺关系、突破要点、逐一化解．

由于H2O（g）的浓度来自反应Ⅰ和Ⅲ，均与本反应中的另一反应物的物质的量相等，所以，本题的突破口为明确反应Ⅱ中各物质的物质的量；解题过程就成为多个反应的多个方程式的联合求解．

假设反应Ⅱ中，CO反应了xmol，则生成的CH3OH就为xmol，Ⅰ中生成的CH3OH则为（ax）mol，Ⅲ中生成的CO则为（b＋x）mol．

根据反应Ⅰ:

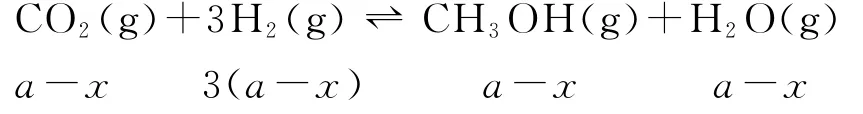
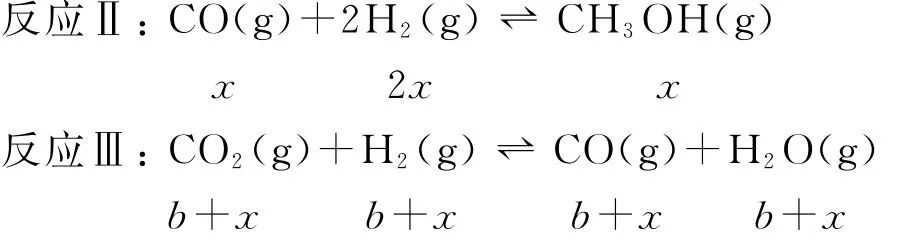
所以平衡时水的物质的量为

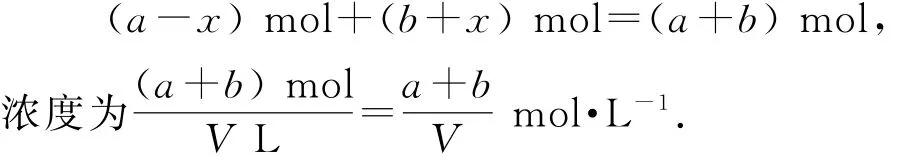
平衡时CO2的物质的量为

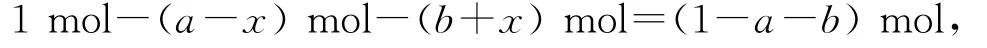
H2的物质的量为

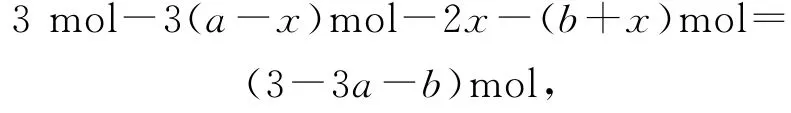
则反应Ⅲ的平衡常数为

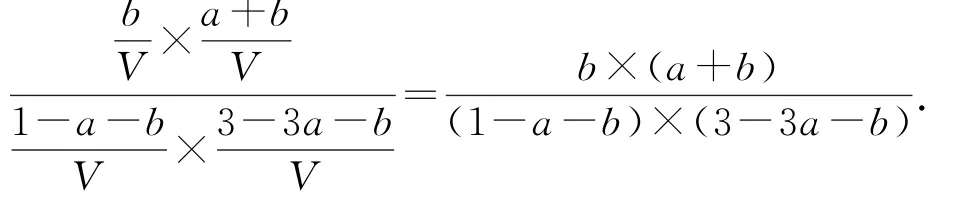
例9（2020年山东卷，节选）某Fe C2O4·2 H2O样品中可能含有的杂质为 H2C2O4·2 H2O、Fe2（C2O4）3，采用KMn O4滴定法测定该样品的组成，实验步骤如下:

Ⅰ．取mg样品于锥形瓶中，加入稀H2SO4溶解，水浴加热至75℃．用cmol·L－1的 KMn O4溶液趁热滴定至溶液出现粉红色且30s内不褪色，消耗KMn O4溶液V1m L．

Ⅱ．向上述溶液中加入适量还原剂将Fe3＋完全还原为Fe2＋，加入稀H2SO4酸化后，在75℃继续用KMn O4溶液滴定至溶液出现粉红色且30s内不褪色，又消耗KMn O4溶液V2m L．

样品中所含H2C2O4·2 H2O的质量分数表达式为________．

解析

本题意图清晰，步骤Ⅰ氧化了所有的还原剂，即C2（包括H2C2O4）和Fe2＋；步骤Ⅱ只氧化了Fe2＋；它们与KMn O4发生氧化还原反应，根据得失电子守恒的关系，即可计算出H2C2O4·2 H2O的物质的量．

设Fe C2O4·2 H2O 的物质的量为xmol，Fe2（C2O4）3的物质的量为ymol，H2C2O4·2 H2O的物质的量为zmol，步骤Ⅰ中C2和Fe2＋均被氧化．

根据题意:Mn O－4→Mn2＋、C2→CO2，结合得失电子守恒，则有以下关系:

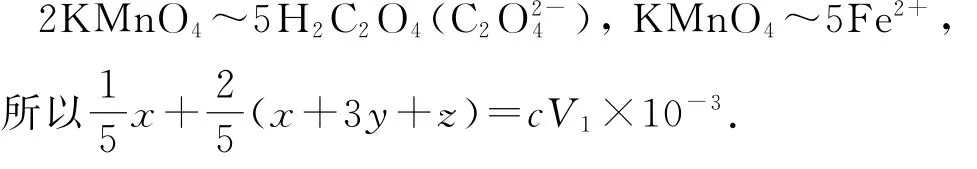
步骤Ⅱ中Fe2＋被氧化，由KMn O4～5 Fe2＋可知，

联立方程解得z＝2.5c（V1－3V2）×10－3，所以H2C2O4·2 H2O的质量分数为

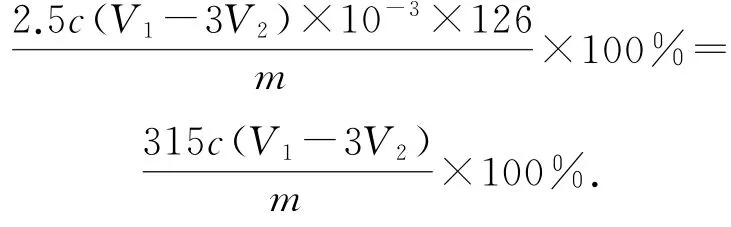
说明这类试题是必考题型，往往用在需要多步运算的重要的必备知识上．体现了“考查重点不回避”的命题特点，多步计算区分度很高，其原因有:1）知识方面的“基础性、综合性、应用性和创新性”；2）思维品质方面的逻辑性、深刻性和严密性．

点评

对此类重点知识的复习与备考，学生要知道“原理来自教材，但内容不同于教材”．无论是新授课还是复习课，学生都要在学习过程中深刻理解、灵活应用；在日常的教与学中，教师要防止“教死书”，而学生则要防止“死读书”，特别是“死记硬背”．这不仅是对知识的理解和熟练应用的问题，也是对“以思维能力为核心的关键能力”培养的很好素材和时机，要防止“眼高手低”“眼勤手懒”，要经常进行针对性训练，定期做一些多步骤、多数据的计算题，既是巩固必备知识，更是保持思维清晰、思维灵活、思维精准、保持心算能力的好方法．

类型4：平衡计算，四重表征，素养为本，能力为先

化学平衡理论是最重要的化学基础理论，既是知识重点，也是能力重点，更是必备知识与必考考点．涉及化学平衡的试题区分度都很高，是部分学生害怕作答的试题．所以，命题专家在这类试题上费尽了心血，把现代化学的“四重表征”[即现象、本质、符号（方程式）和曲线]在本类试题中充分展现．创造性的新颖图表是试题的最大亮点，力求成为学生成绩的区分点．

例10（2020年全国卷Ⅱ，节选）次氯酸为一元弱酸，其电离平衡体系中各成分的组成分数与p H的关系如图4所示．HCl O的电离常数Ka值为______．

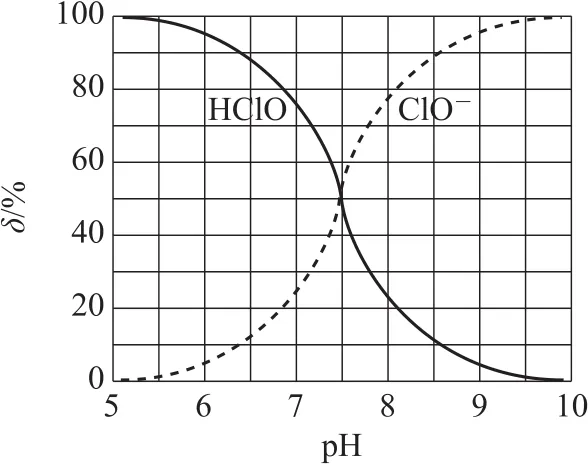
图4

解析

本题是简单地考“必备知识”Ka，但是通过图象曲线的方式进行考查，这就涉及“关键能力”之“理解与辨析能力”和“分析与推测能力”，简单地说，就是能够理解图意，把曲线与化学反应原理对应起来．从常规上讲，曲线都对应很多具体且准确的数值以方便计算，但也有一些是缺少具体且准确的数值的情况．解本题的突破口就是曲线的交点——它们的等值点（这种分析方法称为特殊值法），就有Ka＝，在图象上对应p H 为7.5，即答案为10－7.5．

例11（2020年全国卷Ⅲ，节选）原料初始组成n（CO2）∶n（H2）＝1∶3，在体系压强为0.1MPa，反应（生成C2H4和H2O）达到平衡时，4种组分的物质的量分数x随温度T的变化如图5所示．根据图中点A（440K，0.39），计算该温度时反应的平衡常数Kp＝_____（MPa）－3（列出计算式）．

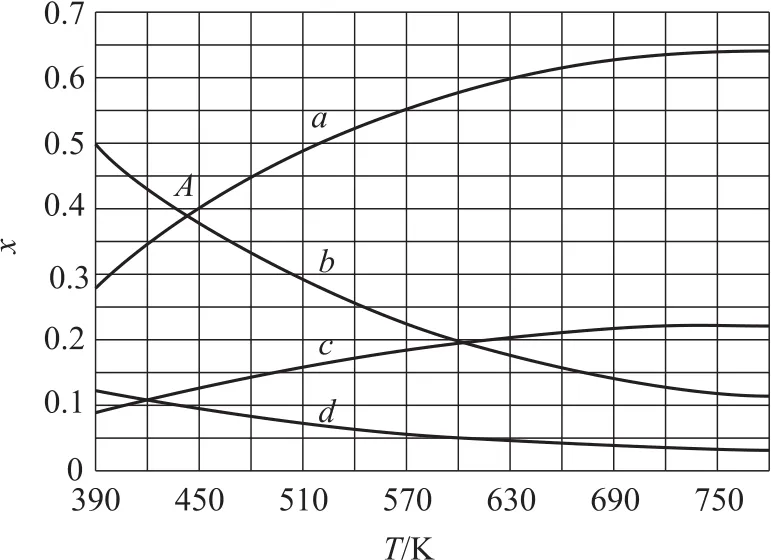
图5

解析

本题反应中共有4种物质，图象中有4条曲线，关键就是判别物质与曲线的对应关系，这在原考试大纲中称为“接受、吸收、整合化学信息的能力”．b和d线是降低趋势，对应反应物；a和c线是上升趋势，则对应生成物．由方程式2 CO2＋6 H2⇌C2H4＋4 H2O知:b线降幅大，对应H2；d线降幅小，对应CO2；同理，a和c线分别对应H2O和C2H4．

具体数值:A点纵坐标对应的0.39，即H2O和H2的物质的量分数都为0.39，由于投料比等于方程式中相关物质的计量数之比，故而推知:C2H4的物质的量分数为H2O的，即的物质的量分数为H2的，即．因此，该温度下反应的平衡常数

例12（2020年全国卷Ⅰ，节选）以酚酞为指示剂，用0.1000mol·L－1的Na OH溶液滴定20.00m L未知浓度的二元酸H2A溶液．溶液中p H、分布系数δ随滴加Na OH溶液体积V（Na OH）的变化关系如图6所示．

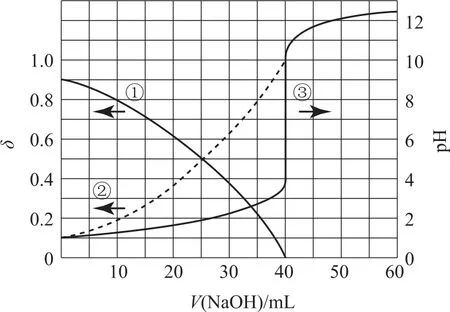
图6

B．H2A溶液的浓度为0.2000mol·L－1

C．HA－的电离常数Ka＝1.0×10－2

解析

首先要读懂图象曲线的意义．曲线③显而易见是中和滴定；曲线②在中和反应完全发生时达到最大值，足见其代表δ（A2－）；从定性的趋势上看，曲线①可能是H2A也可能是HA－，都是减小的趋势，但从定量的角度分析，在起点时，若曲线①代表H2A，则只电离10%，就不会形成p H＝1，所以H2A第一步几乎完全电离，则曲线①代表HA－．

根据图象曲线的计算离不开具体而准确的数值，本题中滴定曲线的数值表现在起点和突变点及突变的中点；另外两条曲线的数值均集中在两个端点；这些数值将与坐标数值和曲线的意义一起用于分析和解决问题．

由“转化”的观点可知:H2A溶液的浓度可以由滴定来求算

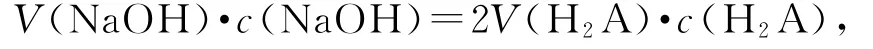
解得c（H2A）＝0.1000 mol·L－1，选项 B错误．把c（H2A）＝0.1000 mol·L－1、曲 线 ① 的 起 点[δ（HA－）＝0.9]、曲线②的起点[δ（A2－）＝0.1]、曲线③起点p H＝1[即c（H＋）＝10－1mol·L－1]代入，就有

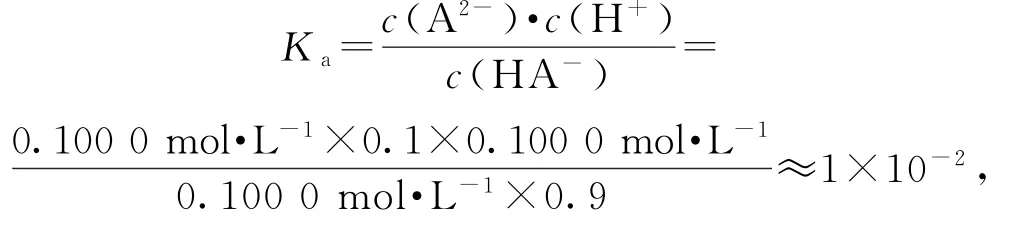
选项C正确．

说明例10中2条明确物质曲线“交点”的等值就解决了Ka值．例11由方程式可确定各线所示物质，由其0.39的物质的量分数，即可推出其他物质，进而代入Kp．而例12中3条曲线都有明确的意义，由曲线的反应原理和对应的数值即可计算，如曲线③是中和滴定，可据此计算c（H2A），由曲线①②是电离，则可把相关数据代入K的表达式计算．

点评

图表既包含物质的种类，也表现反应的趋势，还显现相关的数据，从而定量地描述化学反应及其进程．所以，读图是第一要务:读透图表、读出内涵，建立物质与曲线、反应进程与曲线的关系是解决此类问题的基础性、前提性工作．现代技术促进了化学实验方式、方法的进步，传感器已经成为标准配备．由此，对化学的描述已经由“三重表征”升级为包括“曲线”的“四重表征”．包含图表的新情境试题已经成为现代高考的重要特征．所以，能否迅速而正确地读透图表，不仅决定了能否做出本题，而且直接决定了高考的成败．化学考试大纲中把“接受、吸收、整合化学信息的能力”列为化学学习三大能力之首，足以说明它的重要性．在化学专家对《中国高考评价体系》中“关键能力”的解读中，也把“理解与辨析能力”放在首位，足见其基础性．

化学平衡类的图表信息选择题，是多年来高考化学选择题的压轴题，此类题的立意高，在命题时充分融入核心素养之“变化观念与平衡思想”和“证据推理与模型认知”，对关键能力之“理解与辨析能力”“分析与推测能力”和“归纳与论证能力”都有很高的要求，对中学教学有非常好的启发和导向．

在化学平衡思想的指导下，充分认识曲线的趋势、特殊点的含义、与曲线相关的明确交点和标注点的数据的含义是读图的第一步；用化学平衡原理中相关概念的表达式、关系式或是它们的组合式，去分析或应用于图示关系和数字，从而解决具体问题，这是难点．这一系列的过程都是知识与能力的综合体，都是核心素养的体现，需要学生深刻理解、仔细品味，要经常做一些新形式、新信息、新情境的化学平衡类的图表计算题，并自我总结感悟，才能促进自己对化学平衡原理这一高难度的“必备知识”有全面而深刻的理解，才能逐步学会科学地读图、识图，才能逐步练就“关键能力”，才能在解决具体问题中提升“核心素养”．

3 来自高考试题的感悟

化学计算与化学概念、化学原理相辅相成，化学概念式、方程式及各种关系式不仅表述物质的转化，而且能够精确定量．把“转化”融入化学的概念之中，彰显其价值，越来越多的新观念、新反应、新物质以及新手段的测量、新的表述方式等都将出现在高考试题中，而准确提取出其反应的原理，准确地用化学原理、化学术语和各种关系式来定量表述，实现定性和定量两个维度的深刻分析，正是《中国高考评价体系》中“应用性”“关键能力”“必备知识”融合的体现．

化学计算的数字化结果能够很快验证自己对化学概念和化学原理理解的正确程度及思维的科学性、灵活性、严密性和深刻性．化学计算是原理与推理的结合，是知识与思维的结合，是能力和素养的平台，经常性、规范性和全过程地进行化学计算，不仅有利于深刻理解知识，还能使思维更敏捷、逻辑更清晰，所以，化学计算题是提高学生思维能力的催化剂．

新情境试题伴随着时代发展而生，图表类试题伴随着科技发展和化学的“四重表征”而来，也必将伴随着学生的学习和高考．应用图表的信息与基础知识结合提取其内涵，本身就是学科素养之“证据推理与模型认知”，大量与化学平衡相关的图形曲线让人眼花缭乱，但学科素养之“变化观念与平衡思想”则是科学的火眼金睛．所以，用“必备知识”“关键能力”和“核心素养”来审视新图表、研读新信息、科学做好计算题，是巩固与发展同步的捷径，是助力能力与素养提升的好平台．