立足基本图形的初中几何探究复习课设计

【源起】

笔者观摩了一节以初中数学课本(浙教版)八上2.2 等腰三角形的性质的课内练习2 为引，在九年级上的一节探究性复习课。A教师立足课本，关注探究再拓展，但学生对问题的解答暴露以下教学设计的问题。

一、缺少学生需要的基本图形意识和转化思想的培养

在例题与练习都是以等腰三角形为条件的情况下，但最后的练习题出现了等腰梯形，九年级的学生怎么也想不到把等腰梯形转化为等腰三角形。

二、探究结论多，没有找出各纵论之间的共性，探究价值没有体现

【设计修改】

笔者以基本图形为主线对本课的例题练习重新编排，设计问题串，在八年级基础比较一般的平行班作为等腰三角形的一节复习探究课重新讲了一次，获得了很好的效果。

环节一(初探，生成结论，形成问题解决的基本方法)

例1.如图1 在等腰三角形ABC中，AB=AC，P为BC的中点，则点P到AB，AC的距离相等，请说明理由。

图1

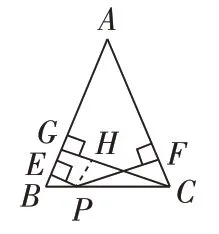
图2

追问1：点P到两腰的距离与等腰三角形腰上的高有什么数量关系？

追问2：如图2 若将底边上的中点变为底边上任意一点，其他条件不变，结论还成立吗？

猜想并证明结论1：等腰三角形底边上的点到两腰的距离之和等于腰上的高。

环节二(练习巩固，提升基本图形的化归能力与识别)

练习1：如图3，在等腰梯形ABCD中，AD∥BC，AB=CD，点P在底边BC上，PE⊥AB于E，PF⊥DC于F，BG⊥DC于G。证明：PE+PF=BG

图3

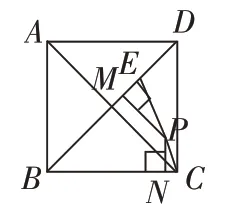
图4

图5

教师引导：点P的情况及问题没有变，但图形变了，那么怎么办呢？

(引导学生把等腰梯形化为等腰三角形直接应用结论)

练习2：如图4，已知正方形ABCD的边长2，E是对角线BD上一点，BE=BC，P是EC上任意一点，PM⊥BD于M，PN⊥BC于N，求PM+PN的值。

练习3：如图5，在Rt△ABC中，∠A=900，D为AB上一点，AD：BD=1：3，BD=DC，P为BC上一点，PE⊥AB于E，PF⊥DC于F，若BC=4，求PE+PF的长。

环节三(例题再探)

教师：前面例1 中的点P位置还可以在哪里？(学生进行大胆讨论，分类画图)

例2.如图6，在例1 的条件下，若将等腰三角形的底边上任意一点变为底边延长线上任意一点，其他条件不变，结论还成立吗？

图6

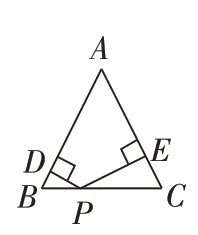
图7

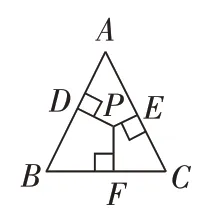
图8

图9

猜想并证明结论2：等腰三角形底边延长线上任一点与两腰的距离之差等于一腰上的高。

例3.已知等边∆ABC和点P，设点P到∆ABC三边AB、AC、BC的距离分别是h1，h2，h3，∆ABC的高为h，若点P在一边BC上(图7，此时h3=0，可得h1+h2+h3=h，请你探索以下问题：当P点在∆ABC内(图8）和点P在∆ABC外(图9)这两种情况时，h1，h2，h3与h之间有怎样的关系？请写出你的猜想并简要说明理由。

猜想并证明结论3：P点在等边∆ABC内，有h1+h2+h3=h；点P在等边∆ABC外，有h1+h2-h3=h

【设计总结】

笔者认为几何探究复习课的设计要考虑以下几个方面。

一、明确基本图形——教师的任务是引导学生观察图形，培养图形意识

由本节引例来源确定基本图形就是“等腰三角形”。

二、确保整节课探究过程的完整性，思维的延续性

本课探究的基本过程设计可以归纳为是：

环节一：原基本图形中，某一要素①在特殊情况下的结论证明；②在一般情况下的结论猜想；③在一般情况下的结论证明；④一般性结论的应用。

环节二：原基本图形特殊化后，同一要素在一般情况下的结论猜想与证明。

三、以基本图形为主线，保证图形变化的有序性

本课以等腰三角形底边上的点的位置变化为主线，初探与再探时从点P在等腰三角形底边中点，到点P在底边上再到点P在底边的延长线上，后继点P在等边三角形内，点P在等边三角形外。从特殊到一般，再从一般到推广的发展过程。

四、从探究问题的结论上要体现共性

本课先是基本图形为等腰三角形时的和关系，然后是差关系，再到基本图形特殊化为等边三角形后的和与差的关系。不但让学生能够真正了解问题探究的一般过程，同时让原来的五个不同结论在整体上统一成都是研究“一点到边的距离与一边上的高线之间的数量关系”。