基于四元数的三维坐标转换在大型LNG钢结构工程建造测量中的应用

葛仁磊，李家军，杨现阳，张 健

(海洋石油工程股份有限公司，青岛 266520)

0 引 言

在高精度大型工程测量中，建造坐标系往往基于自身的局部参考坐标系，与设计安装坐标系不统一，会影响工程建造质量和进度[1-2]，需要进行三维坐标转换实现建造坐标系和安装坐标系的统一。传统的三维坐标转换模型一般用欧拉角构建旋转矩阵，计算过程复杂[3-5]，四元数几何意义明确，计算速度快，可表示所有旋转，无奇异值[6]，非常适合空间大角度三维坐标转换计算。本文基于单位四元数构造旋转矩阵，引入最小二乘原则，实现了高精度大型LNG钢结构甲板片建造坐标系与安装坐标系的统一。与传统计算方法相比，该方法可快速实现三维坐标高精度转换，提高工程建造速度和精度。

1 四元数基本介绍

三维空间的旋转用四元数可表示为[7]

q=w+xi+yj+zk

(1)

其中：

(2)

四元数旋转公式为

(3)

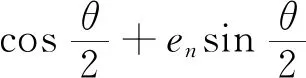
2 基于四元数的最小二乘坐标转换

点Fi和Di的坐标关系可由旋转矩阵R和位移矢量T表示：

(4)

利用四元数法可以方便地求解出旋转矩阵R，根据式(3)，令

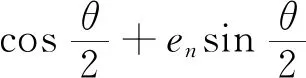
w2+x2+y2+z2=1

(5)

将式(5)代入式(3)并整理，得

(6)

w、x、y、z除了满足限制条件式(5)外，将式(6)代入式(4)，得到误差方程：

即

(7)

式(6)中共有w、x、y、z、Tx、Tx、Tx7个参数，且有一个限制条件：w2+x2+y2+z2=1，w≥0。本文使用基于最小二乘的条件平差进行解算，由于误差方程(7)并不是线性函数模型，需要对函数模型进行线性化后迭代解算，初始值的先验估计可使用任意三点进行。

3 实例应用及分析

本文以海洋石油工程股份有限公司在建某大型高精度LNG钢结构甲板片建造为例，该甲板片结构模型及设计坐标如图1所示，尺寸为32 m×40 m，结构轴线为4 m×5 m，共20个关键节点，各节点坐标公差要求为±5 mm。施工现场测量数据利用徕卡TS30全站仪，采用自由定向测量获取，测量点分布如图2所示，各点坐标值和对应信息如表1所示。

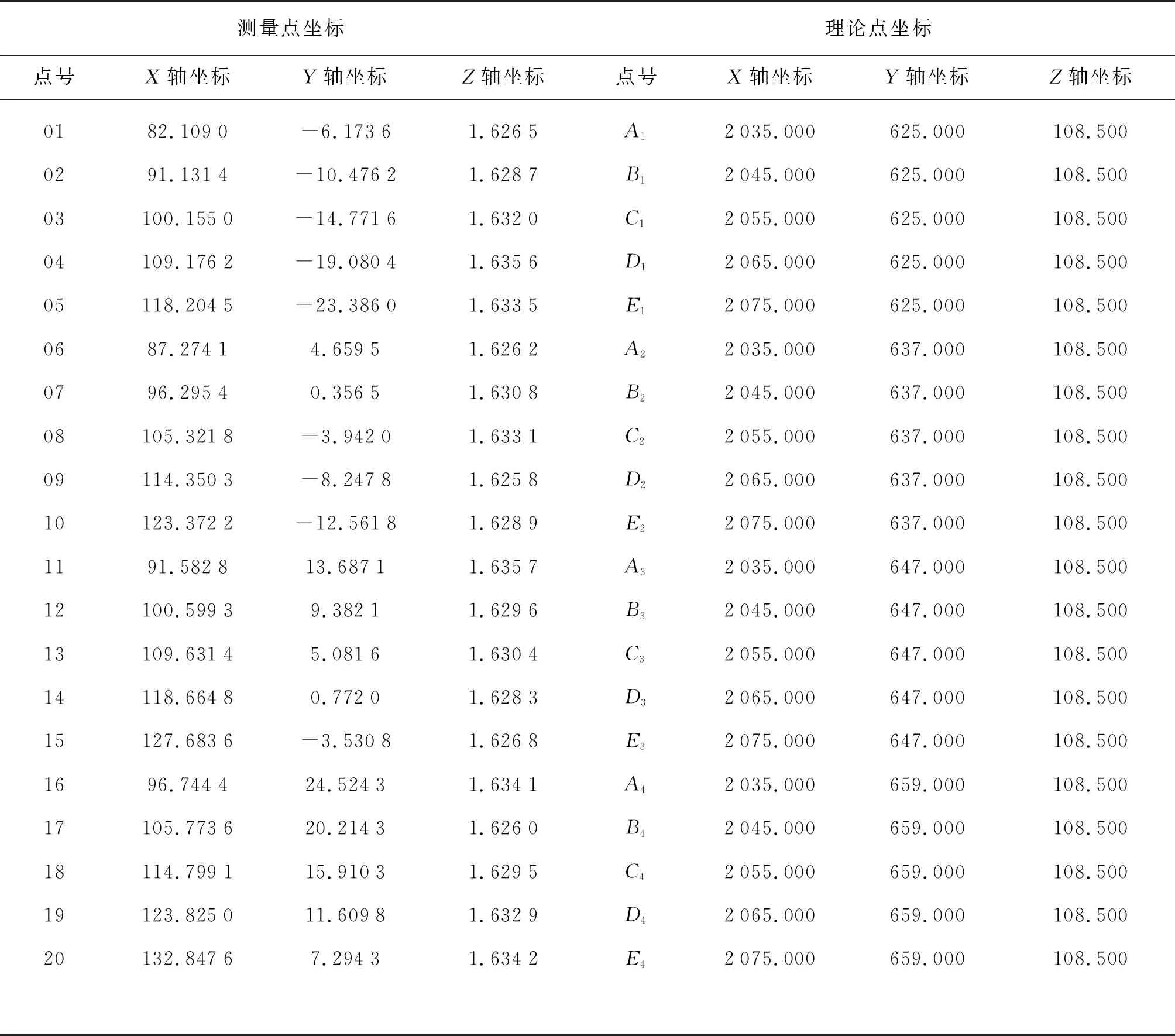
表1 L1-1测量点及理论点坐标 (单位：mm)

图2 测量点分布

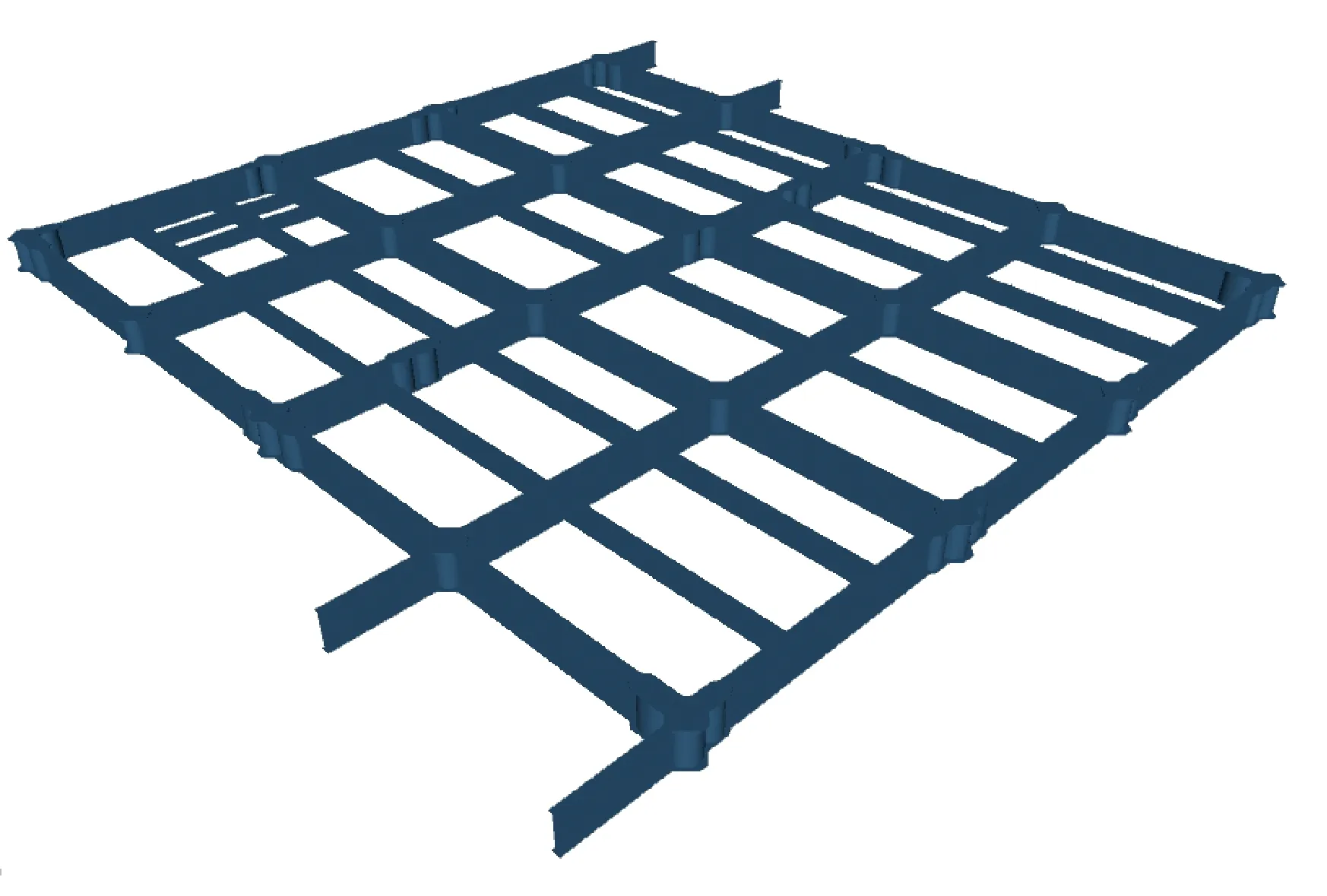
图1 甲板片结构模型及设计坐标(单位:mm)

各理论点坐标为图纸设计坐标，测量点坐标由于采取自由定向测量，导致理论点坐标与测量点坐标之间产生空间旋转，但各测量点与理论点空间上保持一一对应。

3.1 数据计算

3.1.1 传统方法计算

传统计算方法：先计算甲板片水平，再进行水平面投影，以甲板片四条边的中心点为原点建立基于自身的局部参考坐标系，计算各节点偏移。该方法使用条件：需将甲板片水平调至公差范围内，否则会导致尺寸、偏移数据因投影计算而失真。

计算结果如图3所示，甲板片水平值为-63～+62 mm。除C2和D1节点外，皆不符合公差要求，各节点偏移数据中有4个节点Y方向偏移值超出公差要求。按照此计算方法，该甲板片需要调整为水平状态，重新采集数据进行计算，但甲板片尺寸巨大，吨位重，施工调整水平存在较大困难，须耗费大量时间和人力物力，易引起结构变形等质量问题和施工进度。

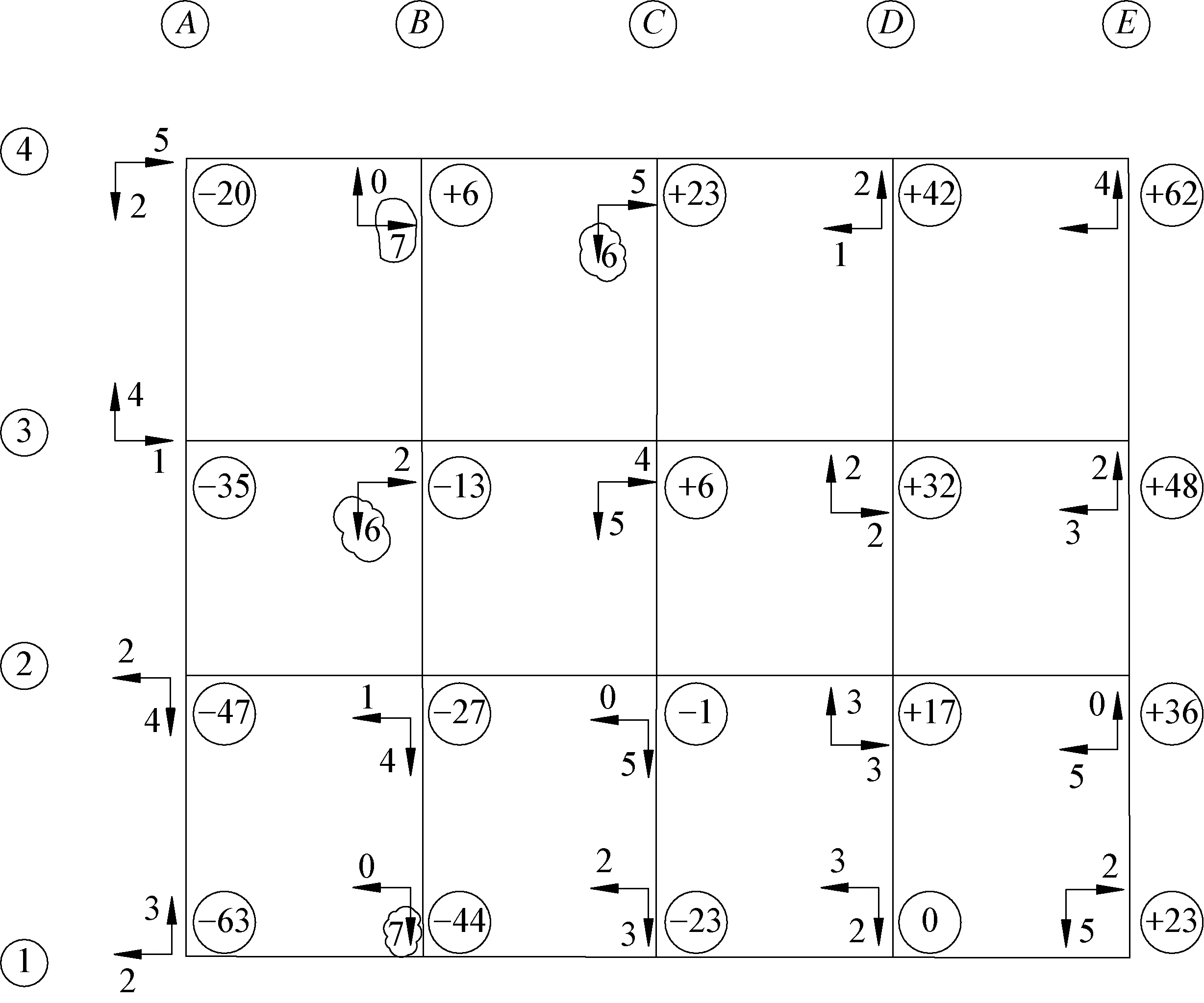
图3 传统方法甲板片计算结果(单位：mm)

3.1.2 基于四元数的最小二乘坐标转换计算

首先，基于最小二乘原则进行七参数的迭代计算，可以按照如下步骤进行：

(1) 将误差方程(7)线性化(具体方法见参考文献[9])。

(2) 进行初始值估计(任意选择三个点，在本例中使用1、2、3号点进行初始值估计)。

(3) 将初始值代入步骤(1)中线性化后的误差方程，并求得七参数据的变化值Δ。

(4) 将初始值与Δ相加，求得最新初始值。

(5) 重复步骤(3)和(4)，直至Δ的值很小，达到旋转精度。

计算结果如表2所示，由表2可知，经过六次迭代计算后，各参数的精度可达到亚毫米级，已经超过全站仪的测量精度，满足计算要求。

表2 七参数计算结果

将得到的七参数进行甲板片各节点数据拟合计算，结果如图4所示，可知各节点水平值为-3～+4 mm，满足公差要求，各节点偏移值皆在5 mm以内，满足公差要求。

3.2 数据对比分析

将图3和图4的数据进行对比计算，如表3所示。

图4 计算结果(单位：mm)

表3 传统方法与四元数法精度对比

由表3可知，采用基于四元数最佳拟合后的数据皆符合公差要求，并且X方向、Y方向和水平值的平均值和均方根值皆大幅降低。原因是采用四元数方法计算时，能够拟合最佳平面，避免了水平调整的巨大工作量，并且该方法以安装坐标系为基准，将拟合误差均匀分配至各点，克服了局部坐标系与甲板片安装坐标系不一致问题，提高拟合计算精度。

为了充分验证基于四元数最佳拟合算法的正确性，总装阶段针对实验模块进行了充分的调整，最终结果如图5所示，与四元数最佳拟合得到的结果(见图4)高度一致，充分说明了该算法的正确性与可用性。

4 结 语

四元数法是一种非常简洁有效的描述物体转动的工具，几何意义明确、计算简单、拟合精度高，是高精度大型工程测量数据计算中最常用的拟合方法之一。本文基于四元数的最佳拟合法，实现了甲板片各节点施工坐标系和安装坐标系之间的统一。与传统计算方法相比，将误差均匀分配至各拟合点，基于四元数的最佳拟合法可大大提高工程施工建造的进度和精度，提高工程测量数据处理的自动化程度，对提高数据的可靠性与规范性、最佳拟合法的编程实现及工程应用都具有很好的指导意义。