考虑土体堆积影响的环保疏浚抓斗推压阻力计算
于金恒,杨 启,陈新权,欧阳义平
(上海交通大学,上海 200240)
0 引 言
国内外疏浚清淤和填海造地工程的广泛开展,推动了疏浚技术与装备的快速发展。“十三五”以来,我国着力于加强河湖水生态保护与修复,政府要求采取环保疏浚方式,减少疏浚过程中底泥对水体的浑浊扰动和二次污染。疏浚抓斗适用于湖河环保疏浚,但封闭式设计也将导致更多土体在斗内堆积,推压阻力计算问题急需解决。
推压阻力由于抓斗底板推压土体破坏变形而产生,与切入阻力、摩擦阻力等共同组成疏浚抓斗挖掘总阻力[1]。推压阻力计算目前主要分为刚体静力学方法和极限平衡方法[2]。刚体静力学方法假设土体抗剪能力达到最大值时出现料楔滑移,对此时滑移的三角形刚体料楔进行受力分析,计算推压阻力[3]。畅启仁、肖乾信等分析散货抓斗抓取物料过程中料楔滑移及受力情况,结合实验数据得出推压阻力公式[1,4]。胡捷运用模型实验的方法,对散货抓斗在取料过程中推压阻力及挖掘曲线做了定性的分析[5]。荷兰代尔夫特大学Miedema等针对重力式疏浚抓斗开展实验研究,基于孔隙水压力和边界料楔现象从本构关系上计算推压阻力[6-7]。张海宁采用Miedema方法计算重力式疏浚抓斗推压阻力,并利用LS-DYNA软件进行了数值模拟[8]。极限平衡方法与挡土墙原理结合,在抓斗开发设计及工程实际中应用广泛。堆土机械、挖掘机械广泛应用朗肯挡土墙理论,假设挡土墙垂直计算推压阻力,在疏浚抓斗上应用计算结果误差较大[9]。上海海事大学郭广松针对重力式长撑杆疏浚抓斗引入库伦挡土墙理论,假设挡土墙转动,得到推压阻力计算的库伦解[10]。许炎林、毛晶将库伦挡土墙理论应用于动力式液压疏浚抓斗推压阻力计算[11-12]。武汉理工大学计三有基于散体变形理论假设,采用对数夹层机构模拟土体破坏面,建立了重力式长撑杆疏浚抓斗推压阻力计算模型[2]。姜益改进了计三有的方法,考虑了斗内土体堆积影响,提出将斗内土体堆积仅以重力形式外加到推压阻力上[13]。
综上所述,国内外疏浚抓斗推压阻力研究仍不完善,斗内土体堆积对推压阻力的影响被长期忽略。刚体静力学方法假设的直线滑移面与实际土体破坏曲面不符,目前在抓斗开发设计中应用较少;挡土墙理论和极限分析方法应用广泛,但目前该方法的各类模型均未能充分体现斗内被挖掘土体堆积带来的推压阻力增加,导致阻力计算结果较实际偏小。本文通过改进现有推压阻力模型,引入各抓斗开度下堆积角β和挡土墙长度LB1C,利用新的挡土墙长度LB1C推压堆积后形成新的土体模型,对比分析各算法推压阻力计算结果及推压阻力各成分计算结果,提高抓斗开合过程中载荷计算的准确性。
1 推压阻力计算模型
1.1 极限分析法原理
图1所示的环保型闭式动力疏浚抓斗左右对称,左、右颚瓣绕中心铰点O以固定角速度ω旋转直至闭合,抓斗依靠液压力和重力实现开合,被挖掘土体被堆积到斗内。抓斗底板受到的推压阻力R与土体极限破坏载荷P大小相等、方向相反。
用传统塑性极限分析方法求解抓斗底板的推压阻力,假设土体为理想塑性材料,满足Mohr-Coulomb屈服条件,假设土体破坏前后物理性质不变。针对挡土墙长度LBC推压土体BEECC的破坏过程,假设一系列土体破坏面形状,并由虚功率原理求解各破坏面对应的破坏载荷,上限定理求解出其中的最小值,即土体极限破坏载荷P1[2],则任一抓斗开度下推压阻力R1为
(1)
式中:B为垂直纸面方向的抓斗刃口长度;Kγ1、Kc1分别为容重系数γ、黏聚力系数c引起的推压阻力、重力成分系数、黏性成分系数,与土体破坏面形状、抓斗挖掘深度及开度、土壤特性有关。
在连续挖掘作业中,被挖掘土体会在斗内堆积,传统推压阻力计算方法忽略了该影响,导致结果偏小。姜益提出将堆积形成的土体B1E2EB重力附加到传统推压阻力计算结果上[13],即式(2)。该方法反映了推压阻力重力成分受土体堆积的影响,但其假设堆积角β等于0,挡土墙长度仍取LBC,未能体现推压阻力黏性成分受土体堆积的影响。
(2)
本文考虑斗内土体堆积影响,通过分析斗内土体运动及堆积特性,求解各抓斗开度下堆积角β和挡土墙长度LB1C。此时,挡土墙推压土体破坏模型发生了改变,挡土墙长度LB1C较LBC大,被推压土体改为堆积后形成的土体B1E2ECC,Kγ3、Kc3随此时土体破坏面形状改变,得到任一抓斗开度下推压阻力R3:
(3)
1.2 抓斗挖掘过程分析
1.2.1 土体破坏面形式确定
在塑性极限分析中,满足运动许可的塑性变形场称为土体破坏机构。假设的土体破坏机构形式与实际破坏面的拟合程度会直接影响计算结果。相较于挡土墙被动土压力计算问题,陈慧发[14]对比了6种载荷破坏机构,发现对数夹层机构拟合效果较好[14]。计三有、姜益等采用对数夹层机构,推导出了推压阻力计算模型[2,13]。
假设土体外摩擦角δ小于内摩擦角φ,本文选定破坏机构如图2(a)所示。独立变化参数角度ρ、ψ及堆积角β可确定不同的塑性破坏面。引入左右土体干涉系数μ,由式(4)和式(5)求得。μ=0时,左右土体无干涉;μ>0时,左右土体干涉。

(a)

(a)

(4)
(5)
如图2(b)所示,刚性三角形CBM为对数夹层破坏机构的一部分,其速度v1垂直于BM,可分解为垂直于BC的速度v0和沿抓斗底板BC上移的速度v11,两者的关系为
v0=ωLOCcos(π-η-θ-α)
(6)
v11=v0tanρ
(7)
1.2.2 堆积角β及挡土墙长度LB1C计算
初始状态下,抓斗最大张开,抓斗底板与水平面呈90°角。此时抓斗依靠重力切入土壤中,切入深度H0为初始挖掘深度,堆积角β= 0。在油缸推力和抓斗自重作用下,斗体绕抓斗中心铰点O旋转闭合,斗内土体堆积角β逐渐增大,直至最大堆积角βmax。
斗内土体堆积过程如图3所示,考虑到挖掘过程中部分土体散落在斗外,根据质量守恒定律、土体破坏前后物理性质不变的假设,可将被挖掘的土体A1BCA转化为四边形土体B1E1EB和三角形土体B1E2E1。

图3 斗内土体堆积过程示意
抓斗堆积角β小于最大堆积角βmax时,抓斗底板上土体位移LB1B由破坏面速度关系求得,堆积角β和挡土墙长度LB1C由式(8)~式(11)计算:
(8)
SA1BCA=h1(H0+H1)+h2(H1+H2)+…+
hn(Hn-1+Hn) ,n=1,2,…,k
(9)
(10)

(11)
式中:KSC为挖掘土体散落系数;hk为从时间步k-1到k,抓斗底板端点C处移动的水平距离;Hk为从某一时间步k下的抓斗挖掘深度。
当抓斗堆积角β等于最大堆积角βmax时,挡土墙长度LB1C同样可由式(10)求得,但式中LB1B须由式(12)和式(13)联立求解得出。
(12)
LB1E1=LBE+LB1Bcosα=Hcotα+
LOCcos(θ+η)+LOE0+LB1Bcosα
(13)
考虑并描述斗内土体堆积的影响,认为土体A1BCA堆积为四边形土体B1E1EB和三角形土体B1E2E1,将以往算法中常忽略的堆积角β及挡土墙长度LB1C实时计算纳入挖掘破坏面的描述中,改进为计算挡土墙长度LB1C推压土体B1E2ECC破坏过程中的推压阻力。
本文考虑斗内土体堆积对推压阻力计算的影响,主要通过改进挡土墙推压土体破坏模型实现。假设图3中土体A1BCA被挖掘后,在斗内堆积形成四边形土体B1E2EB。传统推压阻力计算模型为挡土墙LBC推压四边形土体BEECC破坏,本文改进为挡土墙LB1C推压土体B1E2ECC破坏。本文引入各抓斗开度下的堆积角β及挡土墙长度LB1C计算,可用于描述挡土墙LB1C推压土体B1E2ECC破坏计算模型。
1.3 推压阻力计算模型确定
本文研究的抓斗挖掘过程考虑了斗内土体堆积,在各抓斗开度上分别计算堆积角β及挡土墙长度LB1C,分别列出内、外力功率,由内、外功率相等确定推压阻力计算模型。参考计三有的论文,由虚功率原理得到抓斗挖掘过程的内外功率方程[2]。
1.3.1 内功率方程
(1) 沿粗糙挡土墙B1C功率D1:
D1=R3Bv0sinδtanρ=P3Bv0sinδtanρ
(14)
(2) 沿刚性三角形底边CM功率D2:
D2=cBLB1Cv0tanρ
(15)
(3) 沿对数螺旋区MBN及曲面MN功率D3和D4:
(16)
(4) 沿刚性三角形底面NP或NQ、QE功率D5:

(17)
1.3.2 外功率方程
(1) 外力P3功率W1:
W1=P3Bcosδv0
(18)
(2) 刚性三角形CBM自重功率W2:
(19)
(3) 对数螺旋区MBN自重功率W3:

(20)
(4) 四边形NBEQ自重功率W4:

(21)
1.3.3 推压阻力计算模型
综上所述,根据抓斗底板推压受力和土体破坏面情况,由虚功率原理确定推压阻力计算模型。根据独立变化参数角度ρ、ψ及堆积角β,可以确定一系列的破坏面形式,进而求得一系列的极限破坏载荷值。由极限定理的上限解求得在一系列极限载荷中,最小值即真实破坏载荷。
已知推压阻力R与破坏载荷P大小相等,外摩擦角δ小于等于内摩擦角φ,建立推压阻力及极限破坏载荷的计算模型见式(3)。
参考计三有论文可知,式(3)中Kγ3、Kc3由式(22)~式(31)求得[2]:
Kγ3=Kγ31+Kγ32+Kγ33-Kγ34
(22)
Kc3=Kc31+Kc32+Kc33-Kc34
(23)
(24)

(25)
(26)
(27)

(28)
(29)
(30)
(31)
2 推压阻力仿真分析
2.1 各算法推压阻力仿真及对比分析
本文所研究的3 m3环保型闭式动力疏浚抓斗模型,选取的抓斗及土壤参数如表1所示。其中,土体在水中的最大堆积角βmax与自身颗粒特性、含水状态和外力条件等有关,参考砂类土水下休止角数据并考虑疏浚抓斗挖掘作业实际,本文取βmax= 20°[15-16]。

表1 抓斗及土壤参数
在MATLAB中建立考虑土体堆积的疏浚抓斗推压阻力仿真模型,与两种传统方法的仿真结果对比如图4所示。曲线“Method1”为传统推压阻力计算方法,不考虑斗内土体堆积,所得推压阻力计算结果明显偏小。“Method2”为姜益提出的推压阻力计算方法,假设堆积角β= 0,单独计算斗内堆积土体重力并将其作为外力添加到推压阻力上。“Method3”为本文算法,可以观察到其推压阻力值明显增大;且随着抓斗转角θ增大至闭合,斗内土体大量堆积,推压阻力加快增大。将抓斗完整闭合一次过程中各抓斗转角θ上的推压阻力累加计算,“Method3”较“Method1”增加约90%,较“Method2”增加约40%,更好地体现了斗内土体堆积引起的推压阻力增加。
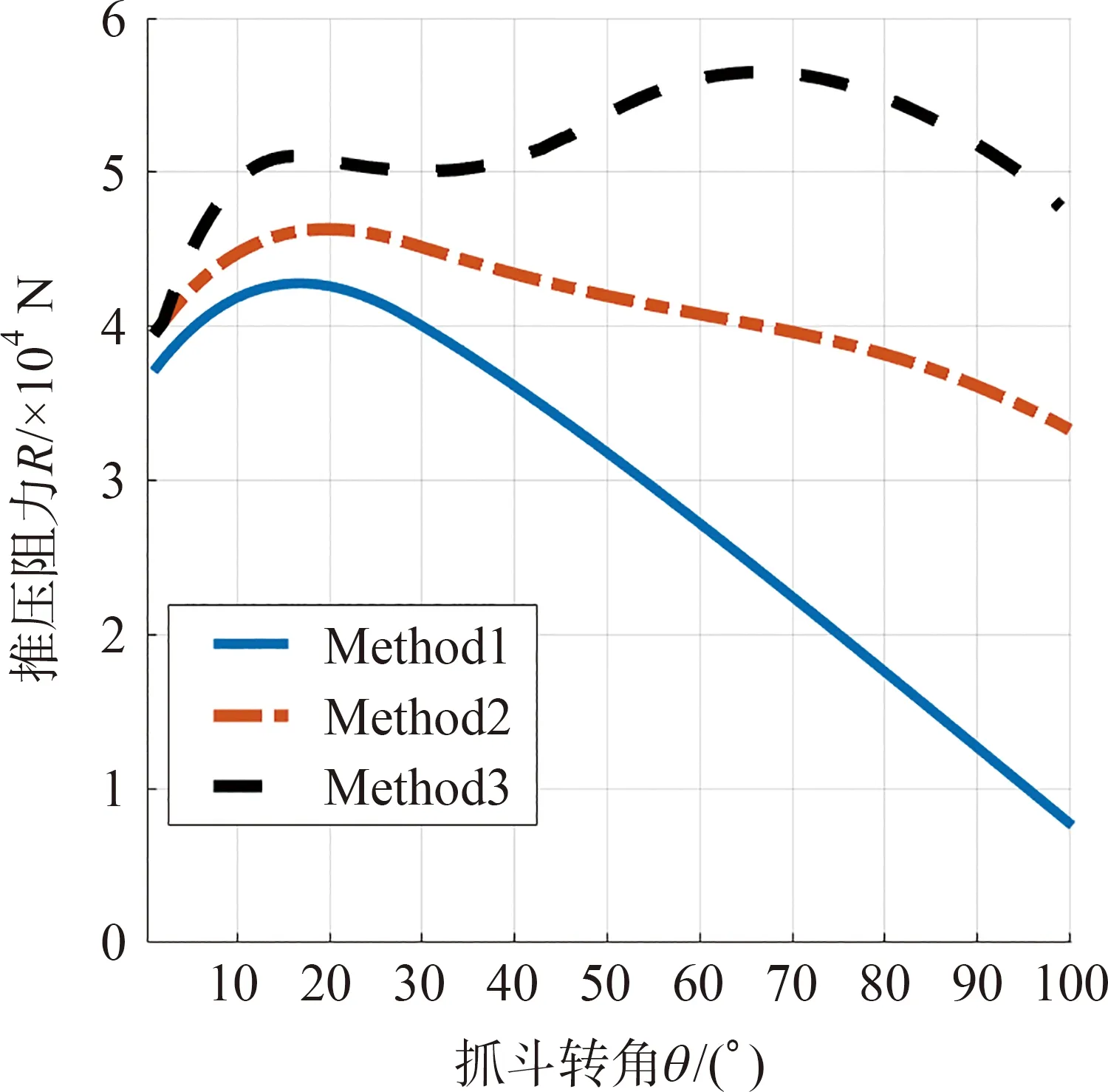
图4 各算法推压阻力仿真结果对比
2.2 推压阻力各成分仿真及对比分析
推压阻力R由土体的黏聚力、重力作用形成,可分为推压阻力黏性成分和重力成分。在MATLAB中建立推压阻力各成分仿真模型,并取不同的土壤黏性或容重系数进行对比分析,理论上能够得到更大的推压阻力黏性成分、重力成分计算结果。
对比各算法推压阻力黏性成分、重力成分仿真结果,如图5所示。在图5(a)中,推压阻力黏性成分曲线“Method3”明显高于“Method1”和“Method2”,抓斗完整闭合一次过程推压阻力黏性成分的累计值增加约35%,验证了本文的算法能够更好地体现推压阻力黏性成分增加。在图5(b)中,曲线“Method1”未考虑斗内土体堆积引起的重力增加,推压阻力重力成分计算值明显偏小;“Method2”与本文提出的“Method3”较为接近,可以相互印证,也说明了斗内堆积土体重力额外附加的方法在一定程度上是合理的。

(a)
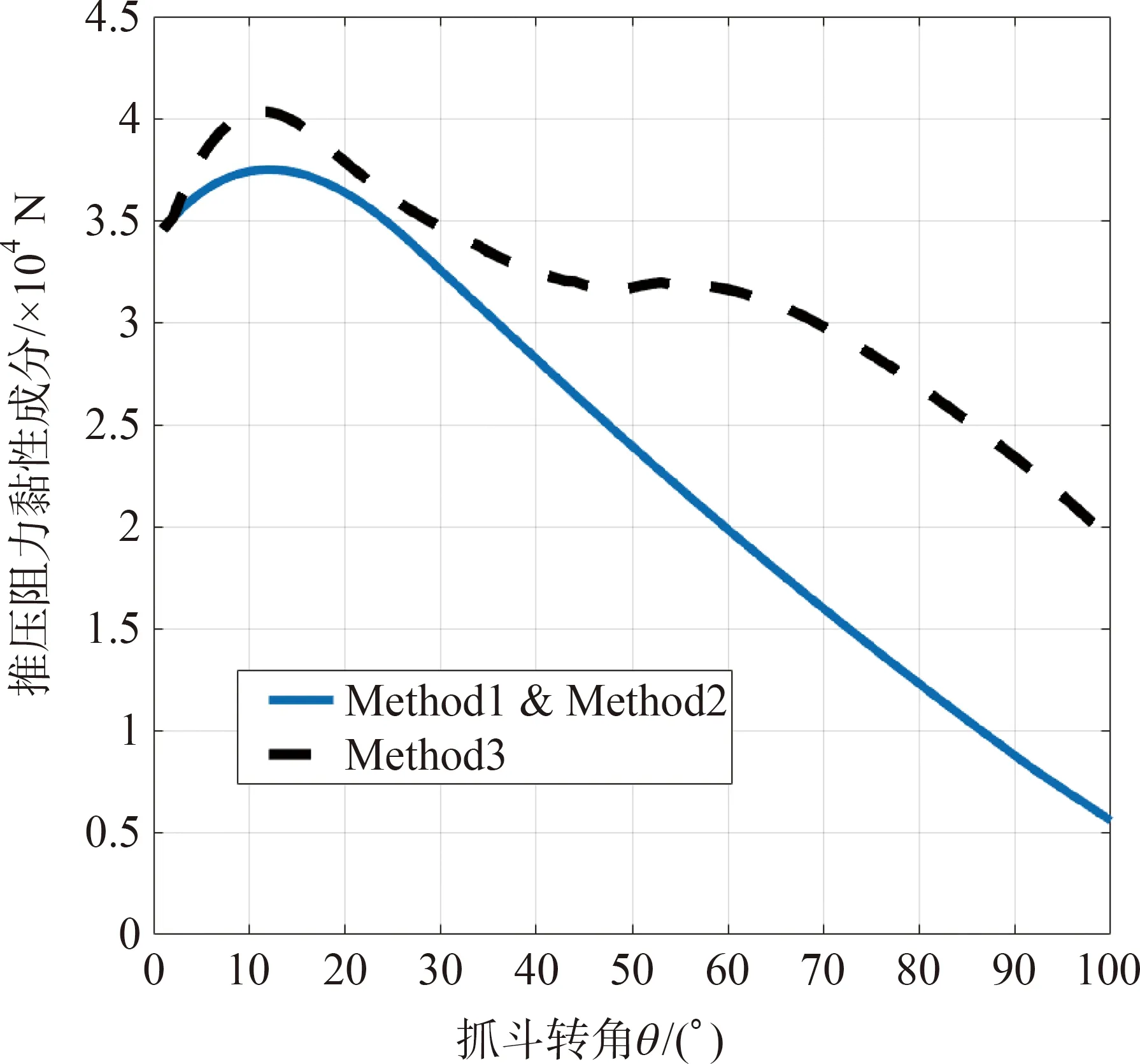
(a)
为进一步探究黏性、容重对推压阻力的影响,本文针对黏聚力系数c、容重系数γ不同取值分别进行仿真及对比分析,结果如图6所示。随土壤黏聚力系数c的增加,土壤容重系数γ分别增加,推压阻力相应增加。而且,随抓斗开度增大至完全闭合,土体逐渐被破坏并堆积到斗内,推压阻力中黏性成分减少,推压阻力主要由斗内堆积土体重力形成,表现为黏聚力系数c增加,对推压阻力R增加的影响逐渐减小;容重系数γ增加,对推压阻力R增加的影响变大。
3 结 语
本文考虑挖掘过程中斗内土体堆积的影响,基于极限分析法原理,选用对数夹层机构模拟土体破坏面,创新性地引入了堆积角和挡土墙长度来表达考虑堆积后土体破坏模型变化,最终由虚功率原理和上限定理,求得疏浚抓斗推压阻力各成分结果并进行对比分析,总结如下:
(1) 本文分析环保型闭式抓斗挖掘过程,引入抓斗堆积角β和挡土墙长度LB1C等参数计算方法,并由此来表达斗内土体堆积对土体破坏模型的影响。
(2) 本文建立了考虑斗内土体堆积的推压阻力计算改进模型,该模型较好地反映了土体堆积带来的推压阻力增加。通过与已有文献和仿真结果对比,本文较传统极限分析法,推压阻力仿真结果明显增大,更准确地分析了抓斗挖掘土体破坏的实际过程。
(3) 本文仿真结果显示,黏性或容重系数较大的土壤推压阻力计算结果增大更为显著;挖掘过程中推压阻力黏性成分先增大后减少,推压阻力重力成分逐渐增大,符合土体逐渐破坏后堆积到斗内的实际工况。
本文所建立的推压阻力计算模型适用于环保疏浚抓斗推压阻力计算,可为该类抓斗设计、液压装置选型等提供理论依据。此外,还可为同样存在斗内土体堆积的其他类别抓斗开发设计提供参考。本文采用虚功率原理、极限分析法原理,对土壤破坏过程、参数选取等进行了一定的工程需要假设,未来仍需在理论研究和试验验证上继续深入探究。

