基于MATLAB 的常微分方程的求解及数值仿真

彭东海

（中山职业技术学院素质教育中心，中山528404）

0 引言

常微分方程是描述客观世界运动变化的有效工具，在自然科学、工程技术、社会学等领域有广泛的应用，是高等数学课程的重要内容之一。对于一些比较特殊的常微分方程，如线性方程、可分离变量的方程、存在积分因子的方程等，人们可以求出其解析解；对于稍微复杂一些的方程，可以借助微分方程定性理论分析解的性态，如渐近性、稳定性、周期性等，而这部分内容，我国现行高等数学教材多不涉及；对于更一般的常微分方程问题的求解常常是困扰人们的一个难题。在工程技术和社会科学等应用领域，人们往往借助于现代计算机技术，对常微分方程进行数值求解或者数值仿真，从而得到相应的微分方程解的基本性态。MATLAB 是用于高性能数值计算和可视化的商业数学软件，其将数值分析、矩阵计算、信号处理、符号计算和图形图像集成到一个易于使用的交互式环境中。在此环境中，通过调用不同模块或工具箱，无需太多传统编程即可表达出来，使得其在工程计算、信号处理、金融建模设计与分析等领域有广泛的使用，此外，MATLAB 还是美国数学建模竞赛最常用的参赛使用软件。

在常微分方程求解方面，针对不同类型的方程与不同问题，MATLAB 提供了有效的求解器，比较典型的如 ODE45、DDE23、BVP4C、BVPINIT 等，分别可以对常见的常微分方程、时滞微分方程、边值问题、初值问题进行相应的求解。结合我们多年的教学经验和学生使用MATLAB 的情况，本文通过实例介绍用MATLAB 相关求解器求解微分方程及对微分系统作数值仿真的基本方法及需要注意的问题。

1 求解常微分方程的解析解

MATLAB 有一个丰富的函数库可用于求解常微分方程，不仅数值计算功能强大，由于MathWorks 公司收购了Maple 的内核，其符号运算的功能也很强大。

二阶微分方程

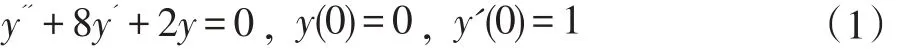
求解代码如下：

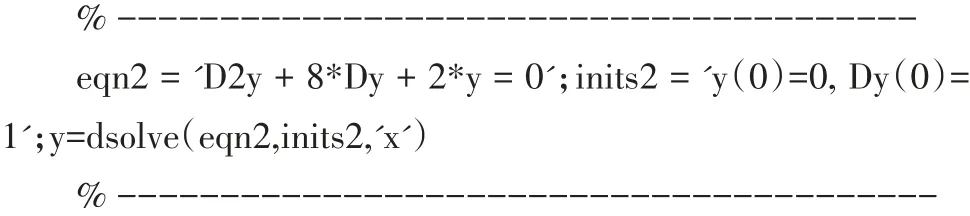
得到方程（1）的特解：

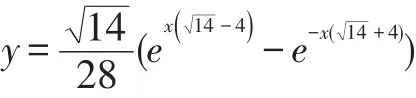
对于线性系统：

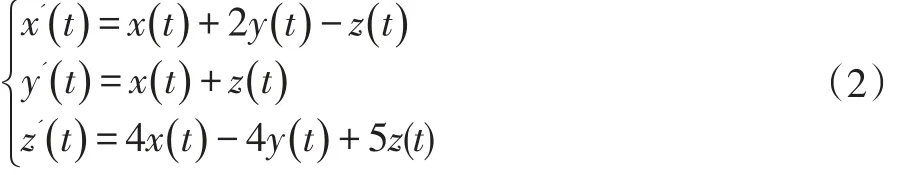
求解代码如下：

得到系统（2）的通解：

2 微分方程数值解

MATLAB 有许多用于数值求解常微分方程的工具。这里主要介绍常用的内置函数ode45 和dde23，它们是基于Dormand-Price 提出的显式Runge-Kutta（4,5）对，属于单步解算命令。

调用ode45 求解器求解给定隐式微分方程：

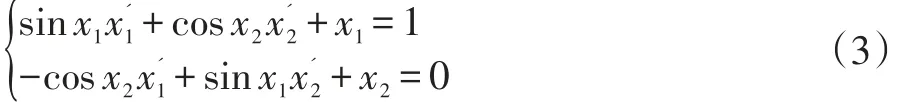
将（3）改写成矩阵形式，令：

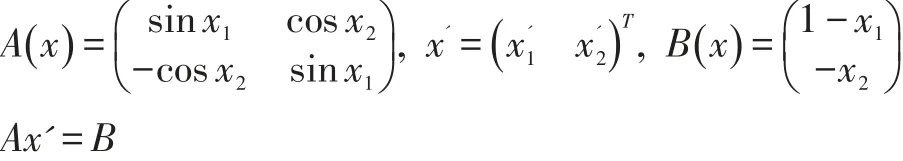
输入代码：

得到方程（3）的解的图像。

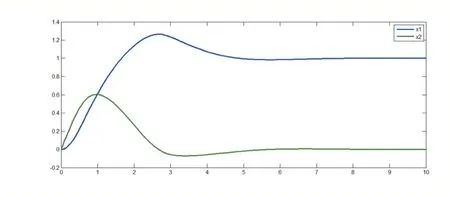
图1 隐式方程的数值解曲线

当然，对于一般的微分方程还有其他的求解器，如表1。

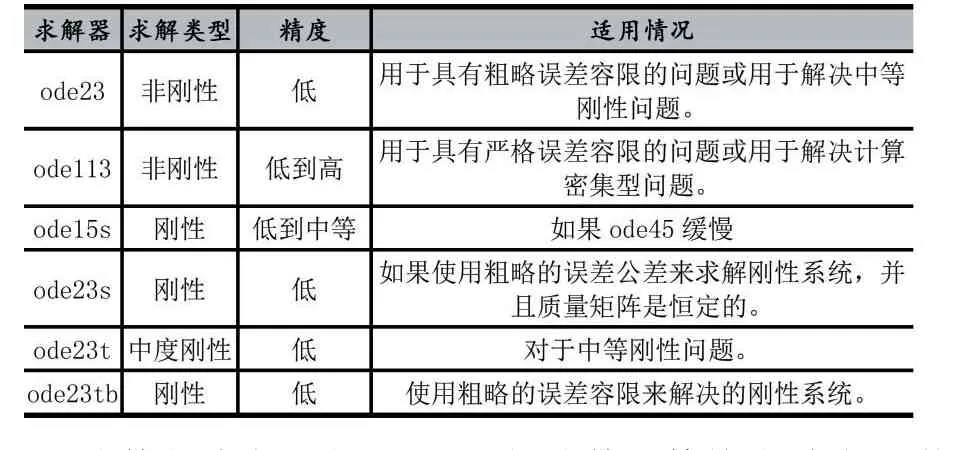
表1

时滞微分方程相对于不含时滞的传统微分方程能够更为准确地描述客观事物的变化规律，数理生态学等研究领域也出现越来越多含有时滞的微分方程模型。但是，时滞微分方程的求解往往更加困难。MATLAB 中提供了 dde23、ddesd 等求解器。

下面介绍应用dde23 求解时滞微分方程，对方程：

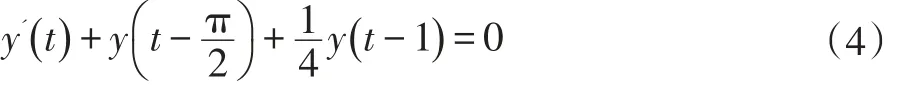
给定y(0)=1，建立一个 MATLAB 的m 文件：

得到解的图像及相位图（图2）。

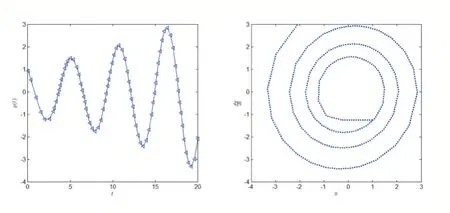
图2

由此可以判断上述方程（4）的解是振荡的。

通常，一个微分方程往往具有许多解，而我们感兴趣的是满足某些特定条件的解。对于边值问题，可以用bvp4c 求解，只须先将微分方程写成一阶微分系统。例如，给定微分方程：

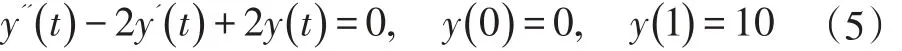
编写bvpexa.m 文件如下：

即可得问题（5）的数值解。

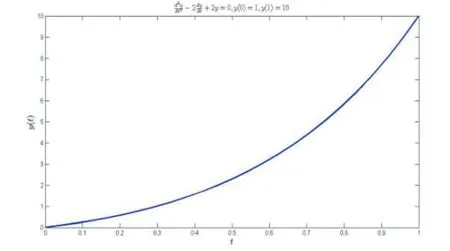
图3

3 常微分方程方向场的绘制

微分方程方向场可以给出微分方程解的几何解释，从微分方程本身的特性了解到它的任一解所应具有的某些几何特征，或者近似的描绘出微分方程解的积分曲线，这就是微分方程方向场的应用所在。

给定方程：

先编写一个m 文件：

然后通过下面主程序代码：

即可得到方向场如下:

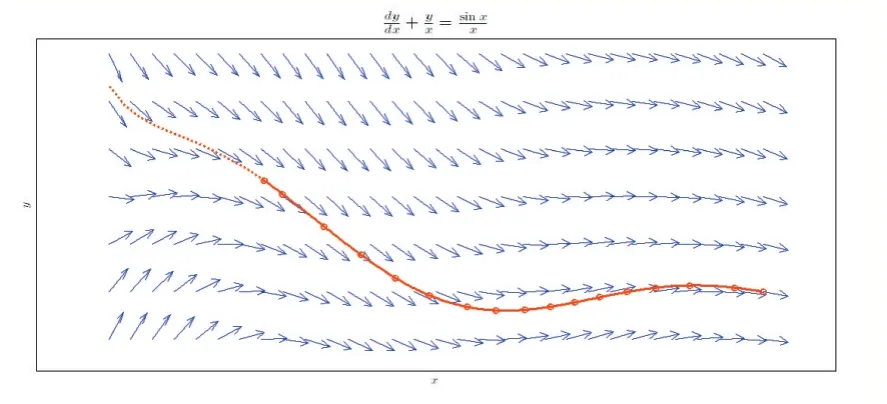
图4

图中4 所示的圆点是方程（8）的初始条件下的数值解，而实线所示为方程的解析解。

的解。

Lyapunov 稳定性定理若有原点的邻域U和一个正定（负定）函数V(x)，使得V˙(x)是半负定（半正定）的，则系统（9）的零解是稳定的，且使得V˙(x)是负定（正定）时，系统（8）的零解是渐近稳定的。

下面是对微分系统零解的稳定性仿真的方法。对给定的系统：

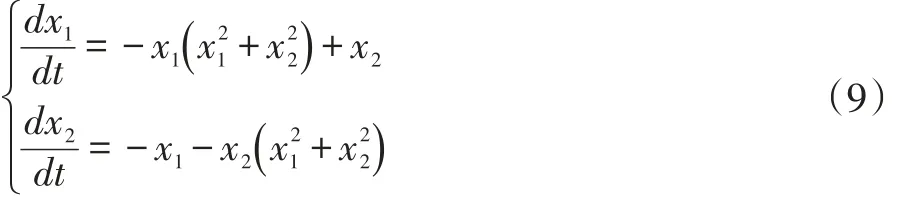
分析构造Lyapunov 函数：

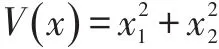
显然这是正定的，同时V(x) 的全导数：

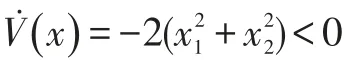
根据上述定理知系统（9）是零解是渐近稳定的。

仿真先编写一个phase.m 程序：

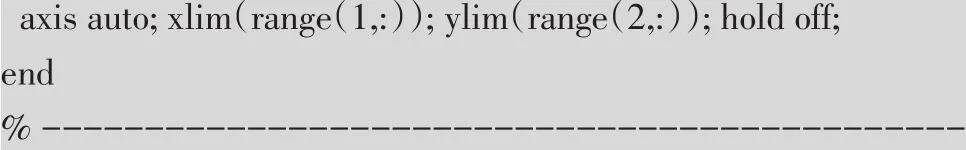
然后通过调用MATLAB 主程序：

得到其稳定性图像仿真。

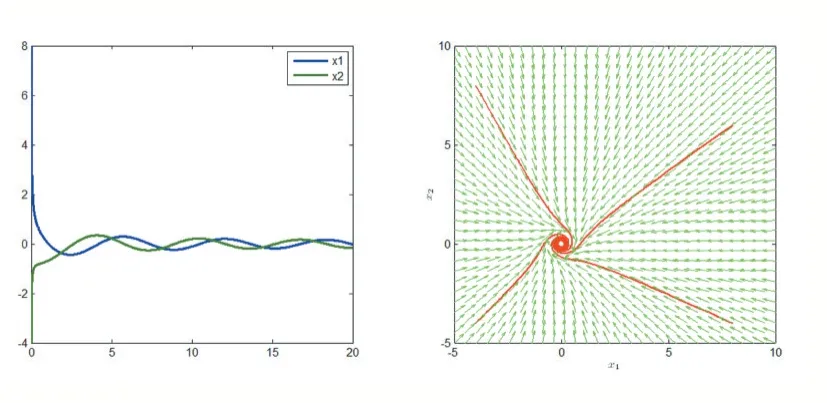
图5

通过对图5 的观察，可以很直观的理解系统（9）的零解是渐近稳定的。

借助MATLAB 的仿真绘图，对考察二维微分系统参数的分支及极限环的存在性时，可以作为理论分析的有效补充，也是很有帮助的。

例如考虑下面微分系统（11）在λ取不同值时零解的稳定性

其中λ∈R。

通过调用phase.m 可以绘制团如图6。

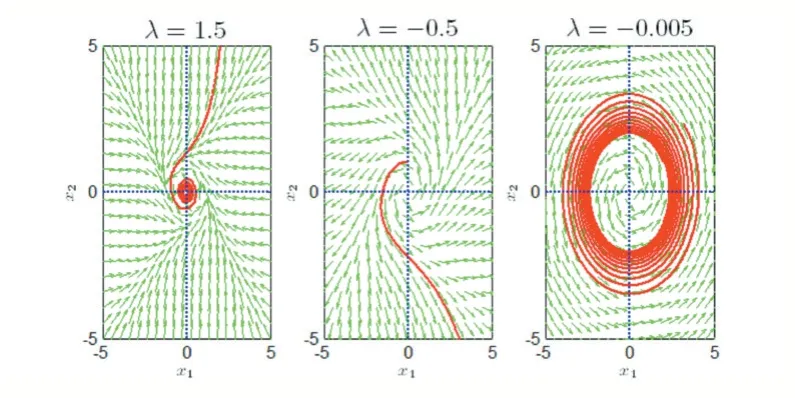
图6

通过观察可以发现λ＞0 时，原点是稳定的；λ＜0时，原点是不稳定的，但是当|λ|足够小时，系统存在极限环。

4 结语

借助MATLAB 软件不仅能进行符号计算求解特定类型的常微分方程的解析解，如常系数线性方程，变量分离型方程，而且能在解析解无法求出时，得到数值解，如非线性初值问题、边值问题、时滞方程等。更重要的是，MATLAB 软件能通过图形图像，直观地展示常微分方程解的性态，如稳定性、渐近性、极限环的存在性等。这些，我们通过MATLAB 的几个典型求解器都做了一一展示。此外，针对实际应用中可能遇到的误差问题，可以通过optimset 对求解器中参数option 进行设置，能够将误差控制在我们要求的范围之内。对于刚性的微分方程，也要注意求解器的选择，否则会造成计算机处理时间过长等问题。另外，在作微分系统定性分析时，数值仿真虽然可以起到直观、快速判断的效果，但是，要得到严格、完备的定性分析结果，我们还是需要回到理论计算上来。

通过MATLAB 的软件我们可以比较方便地实现微分方程的求解和相关仿真，为学生在学习掌握常微分方程的解法和理论时，提供必要的几何直观结果，能激发学生学习兴趣，对提高学生在微分方程的学习效果具有明显的促进作用。