跳出例题悟规律，高效复习提素养

复习课怎样上才能提高教学效率呢？这是所有高三学生和数学教师最关心的问题。有些课堂是以教师为主体的教学思维，教学都是完成任务，这样的教学方式学生永远都是被动学习者，表面上看成绩不错，实则毫无效率可言。其实，高三复习课要想有效率，不是以上课讲什么题，也不是上什么形式的课，而是教师通过课堂这一平台能从数学思想、解题方法、理解能力等方面引导学生，让学生领悟其中的规律，提高复习的效率。

一、反哺教材，加深理解

特别是高三数学第二轮复习，要开始反哺回归，要注重书本上的概念、定义、公式的深层次理解和应用。特别是公式的推导过程的思想方法，就是我们平时解的方法，值得学生“反哺”和深思。

例1.等比数列前n项和公式的推导(q≠1)。

Sn=a1+a2+a3+...+an-1+an

qSn=qa1+qa2+a3+…+qan-1+qan

∴(1-q)Sn=a1+qan

所以当q≠1 时Sn=

这是教材中推导等比数列前n项和的方法——错位相减法，此种方法在处理数列问题时比较常用，但学生却很难熟练掌握。所以通过公式的推导，让学生回归课本，这不是一种简单的重复，而是对数学思想、解题方法的一种重塑、唤醒。这样一方面能使知识得到复习，另一方面也不用通过大量的题目来实现，是真正意义上的“减负增效”的复习课。

二、反思过程，以“史”为鉴

反思往往容易被学生所忽视，它是学生数学思维发展的一个重要方面。课堂上，教师要引导学生检验解题的正确性，完善解题的过程，及时发现并纠正错误。教师还要引导学生反思解题过程，对解题过程进行再认识。为了使本环节对解题起到调节和提高作用，在得到答案之后在课堂上引导学生提出如下问题：推理过程是否严密？表达是否规范严格？有没有错误等等。

例2.已知3 sin2α+2 sin2β=2 sinα，求sin2α+sin2β的取值范围

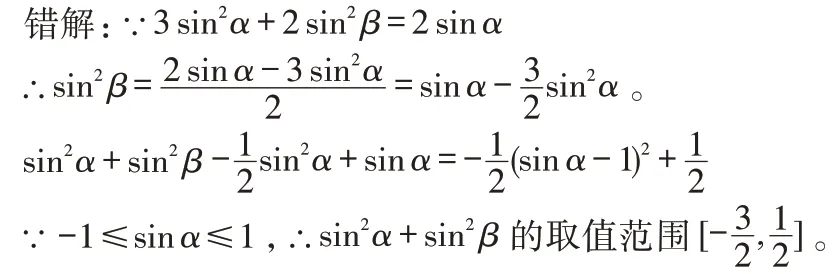
学生没有深挖题目中的隐含条件，而隐含条件显现之后就有助于学生发现并纠正前面的错误，提高准确性。事实上，由2 sin2β=2 sinα-3 sin2α≥0 得0≤sinα≤.

因此0≤sin2α+sin2β≤，即答案应为[0,]

三、辨析差别，一眼洞穿

在数学教学中经常会遇到一类“形相似而质不同”的题目，学生极易受到迷惑将它们混为一谈，在课堂上要将这一类问题放在一起复习，引导学生通过认真对比分析，充分暴露它们之间细微但又是本质的差异，这将大大提高学生分析问题的能力，提高课堂效率。

例3.(1)函数y=3x2-(2m+6)x+m+3 的值恒为非负数，求实数m的取值范围。

(2)函数y=3x2-(2m+6)x+m+3 的值域为非负数，求实数m的取值范围。

这两题很相似，但仔细一想，发现有本质差别，第(1)题中函数y=3x2-(2m+6)x+m+3 的值恒为非负数，是指当自变量x在定义域内取一切值时，所对应的函数y的每一个值都必须大于等于0，而第(2)小题中函数y=3x2-(2m+6)x+m+3 的值域为非负数，是指当自变量x在定义域内取一切值时所对应的函数值必须且只能取到一切大于等于0 的数，由此可见两者貌似相同却大不相同。

四、拓展思维，异中求同

在高三首轮复习中，如何在有限的时间发挥较大的功能？教学经验丰富的教师，可使例题纵横延伸，其中横向延伸主要是指对例题一题多解的探讨，纵向延伸主要是指改变例题的条件和结论，采取变式教学。

如对一些不等式恒成立、有解、无解等问题，学生往往会混淆。

例4.若不等式|x-4|+|x-3|

A.(0，1) B.(0，1]

C.(1，+∞) D.[1，+∞)

有以下两种观点：(1)a大于不等式左边的最小值；(2)a大于不等式左边的最大值。

不等式||x-4|+|x-3|

【拓展1】变式1：不等式|x-4|+|x-3|

不存在x使不等式左边的值小于a；不等式左边的值都不小于a；不等式左边的最小值大于或等于a。

变式2：不等式|x-4|+|x-3|>a在x∈R 上恒成立，则实数a的取值范围是_____。

无论x取何实数，不等式左边所有的值都大于a；不等式左边的最小值大于a。

通过以上两种变式及解答，学生可以体会到在不同的设问下，存在着解答上结构的相似性与表达上的细微细微差别，对题目的特点有一种感性的认识。

【拓展2】不等式|x-4|+|x-3|>a在x∈R 上恒成立，则实数a的取值范围是_____。

无论x取何实数，不等式左边所有的值都大于a；不等式左边的最小值大于a。

【拓展3】不等式x2+2x

无论x取[-2，2]中的任何实数，不等式左边所有的值都小于a2+a-1；不等式左边的最大值小于a2+a-1。

通过三个拓展题，可以帮助学生对题目本质的理解，从而对题目的理解从感性上升到理性，使其真正理解解题的思路和方法。

总之，面对高三数学复习课的繁杂和紧迫，很多学生陷入迷途或困惑，我们不妨试着站在一旁，创建一些精典的例题，引导学生走进去，跳出来，在提高解题能力的同时，审视自己的思考与行为，自我解困，从而走向成熟。从一道道典型例题，提升数学素养，这种教学的思想和教学理念的集中体现，应该是高三数学复习课追求的方向。