精准教学模式下课堂教学设计的探究
一、引言
义务教育数学课程标准指出:“学生获得知识,必须建立在自己思考的基础上,可以通过接受学习的方式,也可以通过自主探索等方式;学生引用知识并逐步形成技能,离不开自己的实践,同时学生在获得知识技能的过程中,只有亲身参与教师精心设计的教学活动,才能在数学思考、问题解决和情感态度方面得到发展。”
让学生能够有效的参与课堂教学中,一直是教师对教学设计的追求,高效的课堂也需要好的设计。笔者针对3.1 平方根这节内容,从两份课堂教学中修改的片段来谈谈自己的感触。首先,本课的重难点都是平方根的概念,而突破难点的关键是抓住平方根概念的本质特征,逐层深入,多角度展示。新课标明确提出,义务教育阶段的数学课程,要从数学本身的特点出发,从学生学习数学的心理规律和学生已有的知识经验出发,让学生经历实践、思考、探索、交流、解释、应用的学习过程,在获得对数学理解的同时,在思维能力、情感态度与价值观等多方面都得到进步与发展。
二、教学设计
1.平方根概念及其性质
(1)原教学设计
某个方队是一个占地约225 平方米的正方形,这个正方形的边长是多少米?
(15)2=225
这个正方形的边长为15 米
引出课题:3.1 平方根
设计:请在括号内填入合适的数字
∵( )2=16,∴16 的平方根是_____
∵( )2=0.49,∴0.49 的平方根是_____
∵( )2=0,∴0 的平方根是____
-4_______平方根.(填“有”或“没有”)
一般的,如果一个数的平方等于a,那么这个数叫做a的平方根(或二次方根)。
平方根的表示:
a(a≥0)的平方根表示为:
读作正负根号a
思考:一个正数有几个平方根?0 有几个平方根?负数呢?
平方根的性质:一个正数有______个平方根,它们________。0 的平方根是________。负数________平方根。
(2)修改后的教学设计
某个方队是一个占地约225 平方米的正方形,这个正方形的边长是多少米?
(15)2=225
这个正方形的边长为15 米
引出课题:3.1 平方根
请在括号内填入合适的数字
( )2=225
( )2=( )
让学生在括号内填入各种可能的答案,然后进行概括。
让学生总结概念:一般的,如果一个数的平方等于a,那么这个数叫做a的平方根(或二次方根)
教师给出:平方根的表示:a(a≥0)的平方根表示为:
学生总结性质:(1)一个正数有2 个平方根,它们互为相反数。(2)0 的平方根是0。(3)负数没有平方根。
设计意图:针对同一个问题简化设计,不用在PPT 中把所有的问题展示出来,把学生要完成的事情还给学生来完成,让学生能够融入课堂中来思考问题,可以提高学生的思维深度,不再停留在表面回答简单的问题,同时部分开放式的教学也有利于教师掌握学生已有的学习知识储备,为后续的教学服务。
2.平方根性质的应用
(1)原教学设计:
说一说:下列式子表示什么意思?

设置练习:
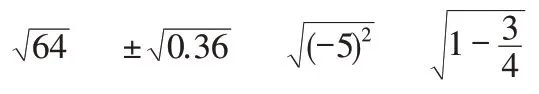
(2)修改后的教学设计:
说一说:下列式子表示什么意思?
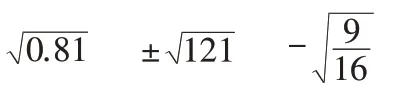
你能自己编写一道题并求出它的值吗?
设计意图:完成例题教学以后要观察一下学生对本次教学内容掌握的程度,设置练习继续去巩固学习的内容。学生的学习只是处在被动学习状态,让学生设计一道题能够观察学生对知识点的掌握程度,根据学生的掌握程度调整教学方法,能够达到高效的教学。
三、设计的感悟
1.提升学生课堂参与的主动性
发现新的知识点需要让学生吸收转化为自己的东西,学生在构建模型的同时是主动构建还是被动构建直接决定了最后的效果,也决定了构建成的模型是不是能够让学生用起来。教师的设计其实学生是一种被动的构建模型,而学生的主动参与是一种主动的构建模型,我们在教学中发现让学生构建的模型转化为自己的模型并能得到有效的应用往往就差过程中的主动性,好的设计能够让学生主动思考和参与教学过程,能够达到事半功倍的效果。
2.简约设计释放学生思维
对于教师的教学设计,我们也可以充分得到简化,我们不需要再繁琐地让我们的设计展示在PPT 上,而是让我们的PPT 得到充分的简化。我们发现一堂课的教学设计在PPT 中展示的只有几页甚至只有几个环节,但是却包含了课堂中学生充分的思维和活动,学生的思维活动是不可以预设的,再精细的课堂预设也不能包含学生的思维。我们的设计只能让学生的思维空间得到大幅度的扩充,设计的简约也包含了大量的学生的思维活动,留给学生大量的思考空间。
3.开放与精准的一次碰撞
很多课堂教学设计束缚了学生的思维能力,让学生随着教师的设计走,学生没有了自己的想法和思路,让课堂变成教师的课堂,看起来教师对课堂的把控性很高。其实,课堂中学生的思维能力培养是有限的。开放式教学中适度地开拓了学生的思维,让学生能够从教师的设计中释放出来,可以拥有自己的想法,充分地展示了学生学习的能力和学生对问题的理解程度,让教师可以随时调整自己的教学,使教学适合自己的学生,这样才能够在课堂上让教师知道学生需要什么,还有哪些是没有掌握的,在精准教学的道路上又迈进一步。

