某超高层钢管混凝土跃层柱计算长度系数分析

乐李辉

（广东省建筑设计研究院有限公司 广州510010）

0 引言

近年来，因城市发展和人们生活娱乐需求的增加，大型商业综合体与超高层等公共建筑项目在城市建设中日益增加。在这类大型公共建筑项目中，超高层建筑往往对竖向构件承载力等相关性能要求较高，钢管混凝土组合结构因其结合了混凝土和钢结构的优点，广泛运用于超高层建筑项目中［1］。同时为了追求大空间的效果，建筑往往要求在大厅或底层区域设置跃层柱［2，3］。相比于普通钢筋混凝土柱，钢管混凝土跃层柱的长细比对其承载力和稳定性都带来一定的影响。我国《高层建筑混凝土结构技术规程：JGJ 3-2010》［4］和《组合结构设计规范：JGJ 138-2016》［5］都提出了考虑长细比对钢管混凝土柱承载力的计算方法，并都规定计算长度系数按《钢结构设计标准：GB 50017-2017》［6］确定。

本文结合相关工程实例，针对钢管混凝土跃层柱长细比计算中计算长度系数相关问题进行探讨，通过对跃层柱的屈曲分析计算得出相应计算长度系数并与文献［6］方法进行对比，并提出跃层柱相应加强措施。

1 计算长度系数μ计算方法

1.1 规范方法

文献［6］附录E 中分别给出了有侧移和无侧移柱计算长度系数方法，其中有侧移框架柱计算长度系数μ按式⑴确定：

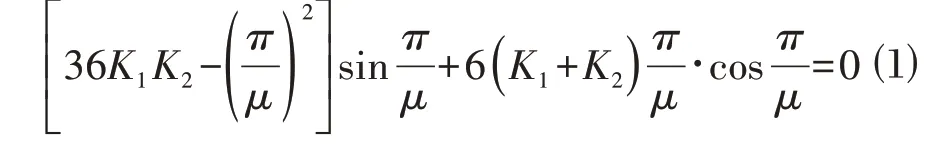
式中：K1、K2分别为相交于柱上端、柱下端的横梁线刚度之和与柱线刚度之和的比值。

通过计算梁线刚度和柱线刚度的比值，查表可得相应框架柱的计算长度系数μ。

1.2 屈曲分析确定

对于跨越多层的跃层柱的计算长度系数可通过对整体结构或局部构件进行屈曲分析的方法得到［7］，主要有整体法、独立杆系构件分析法以及有限元分析法等几种方法［8］。整体法主要是通过把构件放入整体模型中，通过对结构整体模型进行特征值屈曲分析从而得到相应构件的屈曲模态和临界荷载。独立杆系分析法主要通过对柱端实际约束情况进行计算，从而确定柱端支座约束情况，将这些约束施加于独立构件模型中进行构件屈曲分析。有限元分析法也可称为关联构件法，即通过有限元模型建立柱及柱相关联的构件的局部完整结构，将柱端约束情况真实的反映在模型中，再对局部完整结构进行屈曲分析。

由于整体法屈曲分析所得模态能较为真实地反映结构的实际模态，因此得到了广泛认可和运用［9］。本文以整体法为例对跃层柱屈曲分析，得出跃层柱的临界荷载Pcr，通过欧拉公式反推计算长度系数［9，10］：

在整体屈曲分析中，加载模式主要有2 种：①整体荷载加载，即直接采用整体分析时的恒载和活载；②单位力加载，即通过选择相应的跃层柱，在该跃层柱的柱顶端施加单位集中力。这2种方法各有其优缺点，如表1所示。

表1 2种加载方式的优缺点Tab.1 The Advantages and Disadvantages of Two Loading Methods

2 工程分析实例

2.1 工程概况

本文以广东省中山市某超高层为例，工程位于中山市翠亨新区，项目定位为商业办公综合体（分为A，B塔楼，两塔楼为对称关系），塔楼结构总高度为226 m，其中地下2 层，地上53 层。塔楼采用框架-核心筒结构体系，其中塔楼部分框架柱采用钢管混凝土柱，建筑效果如图1所示。

本项目为乙类建筑，抗震设防烈度为7度，基本加速度为0.1 gal，场地类别为Ⅲ类，设计地震分组为第一组。由于底部5 层为商业功能，建筑对部分区域存在净空要求，塔楼首层平面上侧为3层通高商业大厅，有8 根钢管混凝土外框柱在2 层和3 层楼面无楼板连接，仅有单向框架梁连接，且其中1 根柱无任何连接，跃层柱最大无支撑长度达到15 m。结构平面示意图如图2所示。

底部区域钢管混凝土跃层柱柱截面为D1 800 mm×50 mm（直径1 800 mm，钢管壁厚50 mm），混凝土等级为C80，跃层柱相连的上下梁截面均为500 mm×850 mm，混凝土等级为C35。

图1 建筑效果Fig.1 Rendering of Architectural

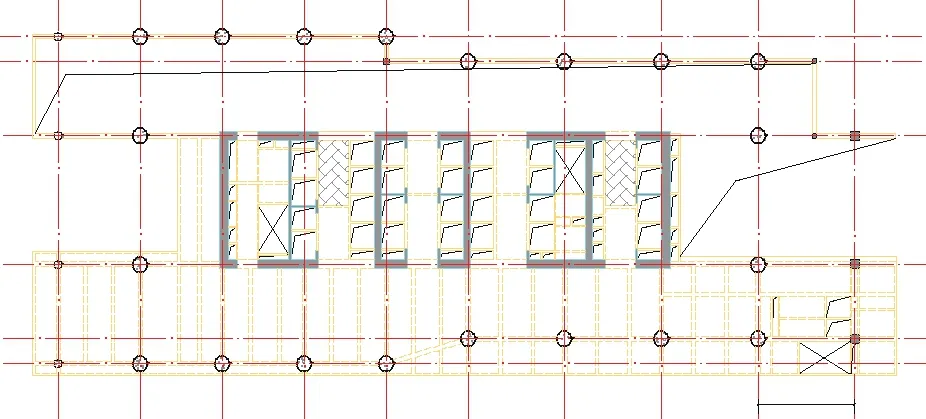
图2 结构平面示意图Fig.2 Schematic Diagram of Structure

2.2 跃层柱屈曲分析

本文采用通用有限元软件Midas Gen 对超高层塔楼底层双向无任何连接的跃层柱进行屈曲稳定分析。为直接得出相应屈曲模态和荷载，选用单位力加载模式，即在跃层柱顶部（4层楼面处）施加单位力，计算模型如图3所示。

图3 Midas Gen计算模型Fig.3 Calculation Model of Midas Gen

图4 为该跃层柱的第一阶屈曲模态，从图4 中可知，对应临界荷载Pcr=3.93×106kN。根据式⑵，计算得出跃层柱计算长度系数μ=0.63。

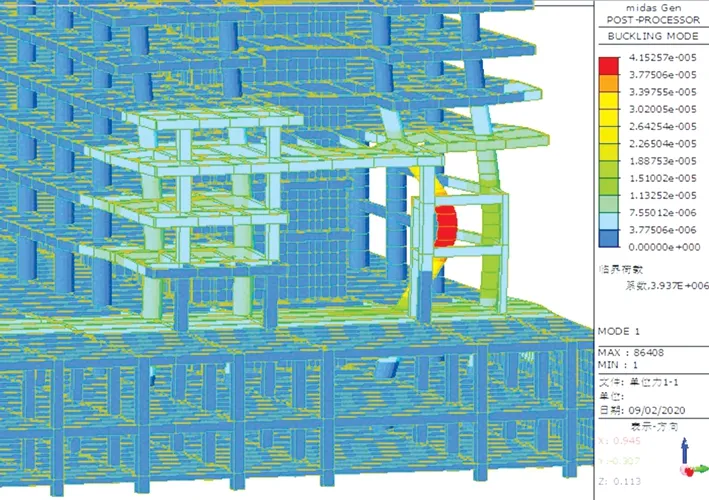
图4 第一阶屈曲模态Fig.4 First Buckling Mode

2.3 结果讨论

文献［4］第11.3.2 条给出了关于钢管混凝土柱的刚度计算：

式中：EcIc为混凝土部分的截面抗弯刚度；EaIa为钢管部分的截面抗弯刚度。

结合文献［6］附录E，计算可得跃层柱无支撑方向上端，柱下端横梁线刚度之和与柱线刚度之和的比值K1、K2均约为0.06，因此跃层柱的长度计算系数约5。由此可知文献［6］计算所得跃层柱的计算长度系数大于屈曲分析结果，这说明由于其算法偏于保守，同时本文的屈曲分析是线性分析结果，未考虑材料几何非线性及初始缺陷等，因此应对线性屈曲分析结果所得计算长度系数进行提高。综上可知，钢管混凝土跃层柱在满足相关文献［6］设计要求后，钢管混凝土跃层柱具有良好的稳定性。

同时结合文献［6］算法可知，可通过加大柱端梁截面方式加强跃层柱的约束作用，以提高跃层柱的稳定性及承载力。同样以本项目为例，将柱端梁截面统一增大到500 mm×2 000 mm，屈曲分析结果如图5 所示，从中可知此时临界荷载为Pcr已提高至4.77×106kN，对应计算长度系数μ提高到0.7。

图5 加大梁截面后第一阶屈曲模态Fig.5 First Buckling Mode after Increasing the Beam Section

3 结论

本文介绍了几种关于跃层柱计算长度系数的分析方法，并通过对中山某超高层项目中钢管混凝土跃层柱进行屈曲分析，得到相应临界荷载，并通过欧拉公式反推得出相应计算长度系数，分析结果表明通过屈曲分析所得钢管混凝土跃层柱的计算长度系数小于文献［6］方法计算所得，钢管混凝土跃层柱稳定性满足相关设计要求。同时提高钢管混凝土跃层柱上下柱端相连梁的截面能有效减小跃层柱的计算长度系数，从而提高跃层柱的稳定性及承载力。