基于整数规划和变换规则优化算法的手术室护士排班模型研究*

□ 杨凯 YANG Kai 曹淑卿 CAO Shu-qing

Objective To research the effect of nurse shift scheduling model based on optimization algorithm of integer programming and transformation rule on the satisfaction with clinical nursing scheduling and quality of work. Methods The nurses from October 2018 to September 2019 in the operating room of a tertiary specialist hospital were taken as the observation group, and nurse shift scheduling model based on optimization algorithm of integer programming and transformation rule was adopted. The nurses from October 2017 to September 2018 were taken as the control group, and the traditional manual shift scheduling mode was used. The two groups were compared for the satisfaction of nurses with nursing shift scheduling and doctors evaluation of nursing quality. Results The satisfaction degree (cooperation satisfaction, workload satisfaction, humanistic demand satisfaction) with the shift scheduling model of the nurses in the observation group was higher than that in the control group. The scores of nursing quality evaluated by the doctors were higher in the observation group (technical specifications, workflow, emergency addressing, equipment nurse cooperation, patrol nurse cooperation) were higher than those in the control group, and the differences were statistically significant (p＜0.05). Conclusion The nurse shift scheduling model based on optimization algorithm of integer programming and transformation rule can improve the satisfaction of nurses and nursing quality.

各级医疗机构中，手术室护士的工作强度及工作量相对较大，为了保证手术护士持续、高效、精准地配合医师手术工作，手术护士排班一直是管理者十分重视的问题。由于排班涉及的限制条件较多、情况复杂，因此建立合理的排班制度尤为重要。整数规划通常用于求解整数变量的最优化问题，通过建立目标函数，如最小化人员数量或工作时间等，设置不同约束条件，包括资源合理消耗、有效工作时间等，求解满足工作需要的最优解。将此模型运用到护士排班中，有利于制定合理的排班方案，减轻护士工作负荷，优化医疗资源配置[1]。变化规则优化算法则是在整数规划模型的基础上，添加排班调整规则，如调整约束条件的优先级规则、调整护士供需规则、班次重分配规则，来满足实际临床工作需要[2]。本研究建立基于整数规划和变换规则优化算法的手术室护士排班模型，使手术室在有限的临床护理资源、高周转率的工作强度下，提高护士的积极性，使医疗资源的利用效率最大化[3]。

Bartholdi将人员排班问题证明为NP-Complete[4]，即在合理周期内无法完整、精确地找到一个满足相应需求的最佳解决方案。关于人员排班的解决方案，大多是采用启发式求解或整数规划求解[5]，除此之外，根据线性或非线性规划、目标规划、混合整数规划模型等解决护理人员排班问题[6]。

资料和方法

1.基本资料。本研究以某三甲专科医院手术室护士为研究对象，构建基于整数规划和变换规则优化算法的手术室护士排班模型，研究和评价其价值。护理规范规定，床护比不得低于1∶0.5，为满足医疗质量控制要求，需设置护士长1名，负责管理日常工作，并相应减少其临床工作量，手术室涉及的护理人员均为女性。将2017年10月至2018年9月，按照传统人工排班模式管理设置为对照组，参与手术室工作的临床医师一并加入问卷调查，基本情况为医师147名，其中主任医师21名、副主任医师42名、主治医师63名、住院医师21名；男性55名，女性92名；年龄25～58岁，平均年龄(39.41±15.32)岁；博士69名、硕士58名、本科及以下20名。2018年10月至2019年9月，按照基于整数规划和变换规则优化算法排班模式管理设置为观察组，参与问卷调查的医师147名，其中主任医师23名、副主任医师43名、主治医师60名，住院医师21名；男性51名，女性96名；年龄27～59岁，平均年龄(41.1±14.72)岁；博士74名、硕士60名、本科及以下13名。两组护理人员及班次的基本情况见表1。

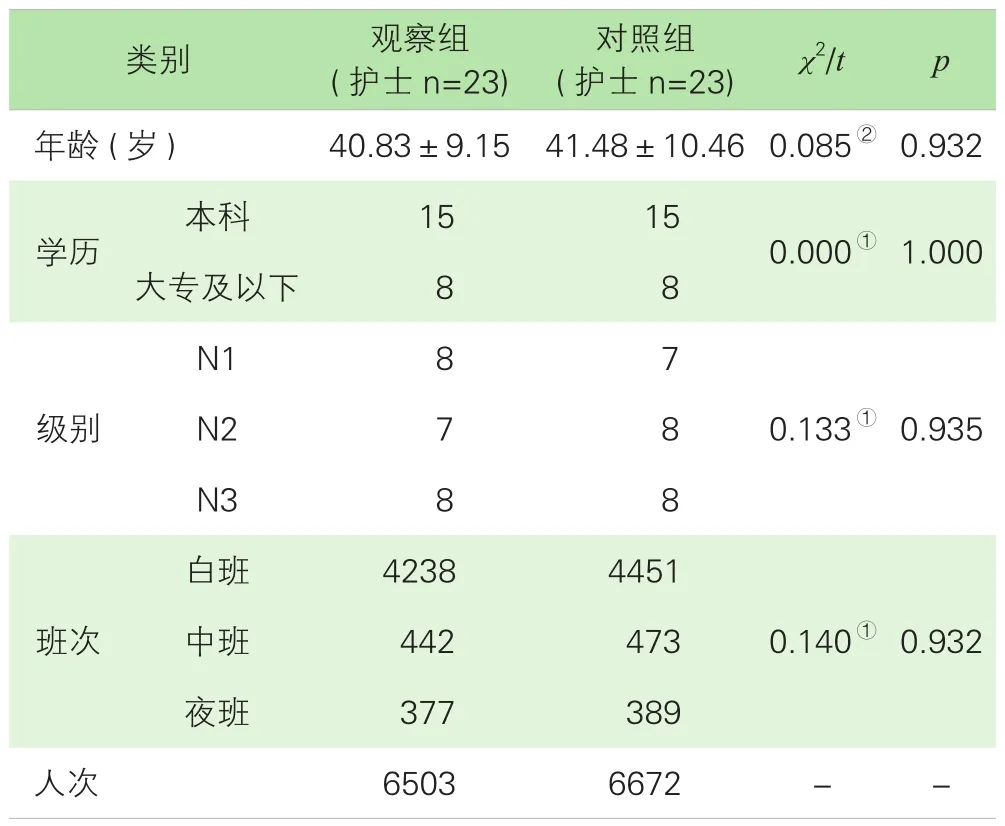
表1 护理人员及班次基本情况

2.建立基于整数规划和变换规则优化算法的排班模型

2.1 参数。模型参数详见表2。

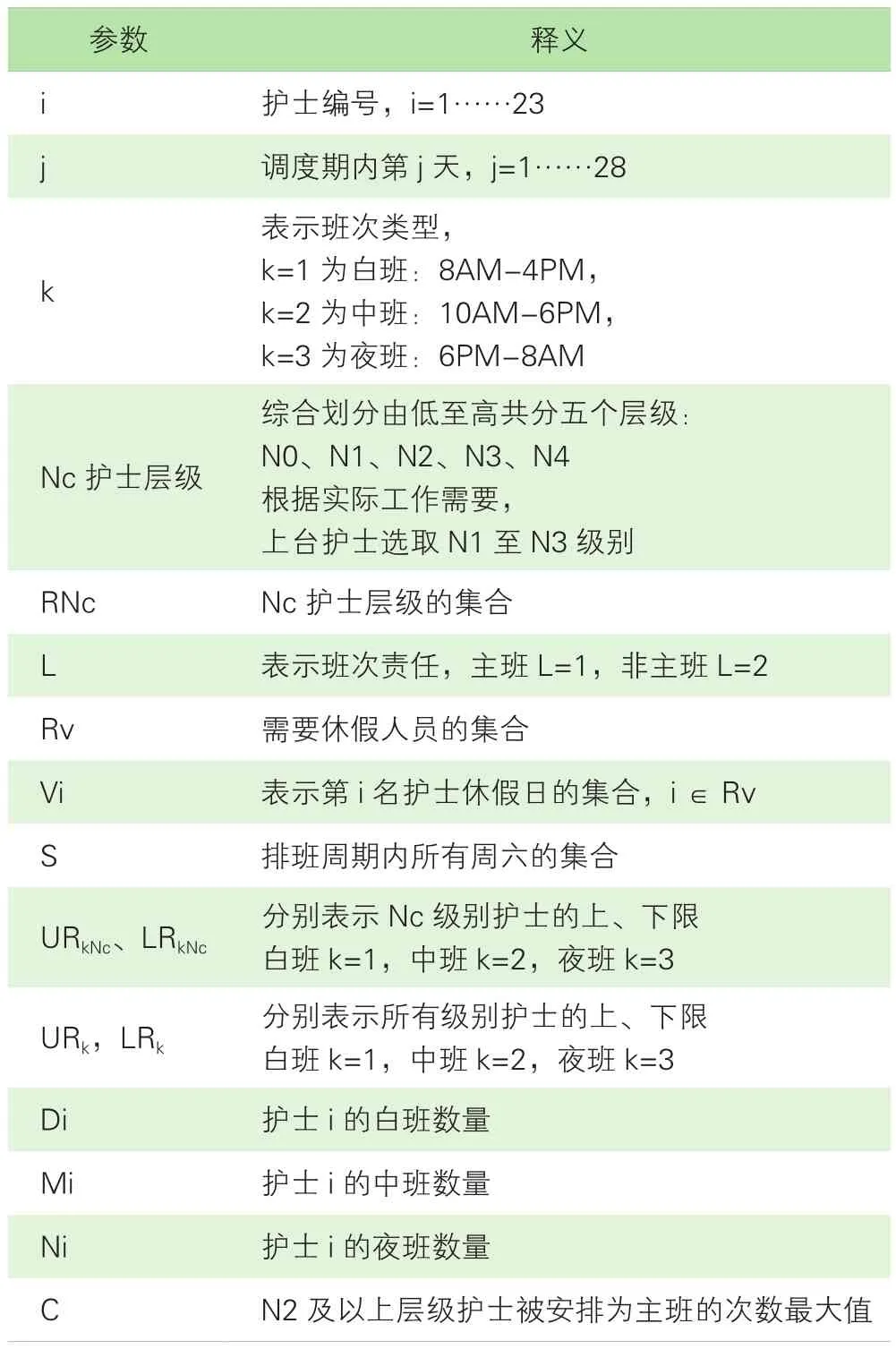
表2 参数释义表

2.2 变量。偏差变量及0～1变量的释义，详见表3。

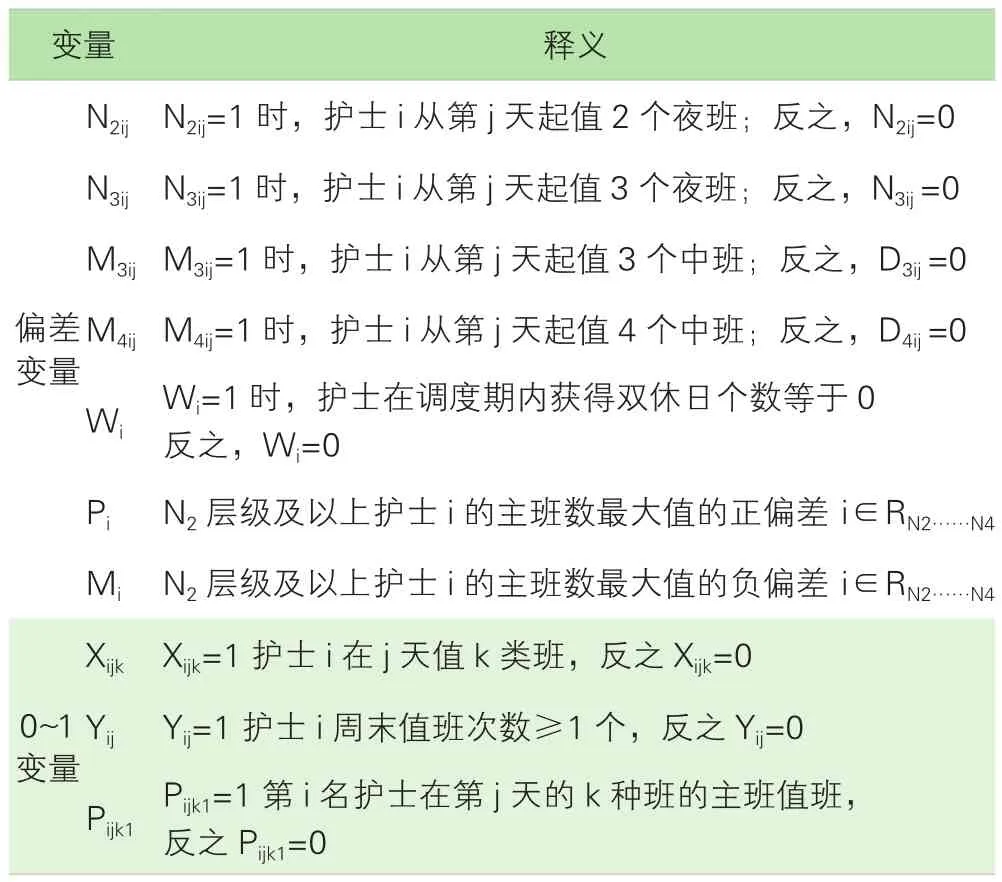
表3 变量释义表

2.3 硬性约束条件

(1)每名护士一个工作日只能值一种班次

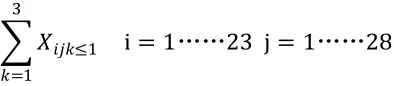
(2)每名护士值完夜班后不能上白班

Xij3+Xi(j+1)1+Xi(j+1)2≤1 i=1……23 j=1……27

(3)调度期内，每个护士的值班数量应该≥21.75

(4)每个班次的NC护士不超过上下限

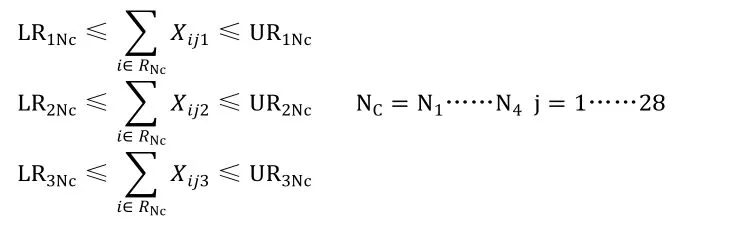
本案例中，根据历史数据总结归纳LR1N3=2，UR1N3=3，LR1N2=2，UR1N2=3，LR1N1=2，UR1N1=3；LR2N3=1，UR2N3=2，LR2N2=1，UR2N2=3，LR2N1=1，UR2N1=2；LR3N3=2，UR3N3=2，LR3N2=1，UR3N2=2，LR3N1=1，UR3N1=2。

(5)每个班次的所有护士不超过上下限

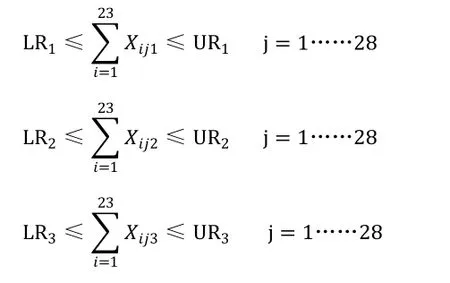
本案例中，每个白班护士总数至少为6名，最多为9名，每个中班护士至少为3名，最多为7名，每个夜班护士至少为3名，最多为6名。

(6)每个班次需要一个主班且该主班在同一班次值班

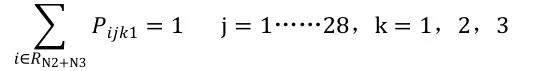
(7)在规定休息日不安排任何班次

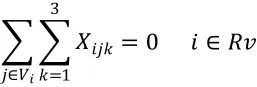
2.4 软性约束条件。软性约束针对护士工作偏好，制定较为灵活的约束条件。

(1)每个护士不应连续值2个夜班

Xij3+Xi(j+1)3-N2ij≤1 i=1……23 j=1……27

Xij3+Xi(j+1)3+Xi(j+2)3-N3ij≤2 i=1……23 j=1……26

(2)每个护士不应连续三天值中班

Xij2+Xi(j+1)2+Xi(j+2)2-M3ij≤2 i=1……23 j=1……26

Xij2+Xi(j+1)2+Xi(j+2)2+Xi(j+3)2-M4ij≤3 i=1……23 j=1……25

(3)每个护士在每个周末至少能休息一天

Xij1+Xi(j+1)1+Xij2+Xi(j+1)2+Xij3+Xi(j+1)3-2Yij≤0 i=1……23 j∈S

Xij1+Xi(j+1)1+Xij2+Xi(j+1)2+Xij3+Xi(j+1)3-Yij≥0 i=1……23 j∈S

(4)本文以28天，即4周为调度周期，为了满足在调度周期内护士至少有一个双休日，应

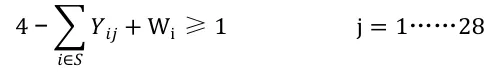
(5)护士层级高级别的人员应平均分配到每个班次的主班

本例中C=8

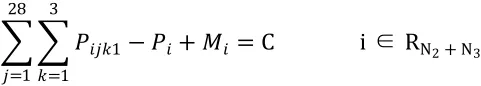
2.5 用层次分析法变换规则优化算法。由于专科医院的临床手术病种一般具有季节性和周期性，所以软约束条件中的偏差有不同的权重，而且权重随临床工作量的变化而变化，运用层次分析法比较约束条件的优先级，用变换规则来优化算法，以确定的变量系数，达到排班的效果具有临床适用性和资源优化性。采用yaahp12.1软件进行层次单排序及一致性检验，临床科室主任与手术室护士长以高发病种时临床需求为依据，测算相应的规则优先级。一致性检验，λmax=6.1960，C.R.=0.0311＜0.1，可以接受。判断矩阵和规则优先级，详见表4。

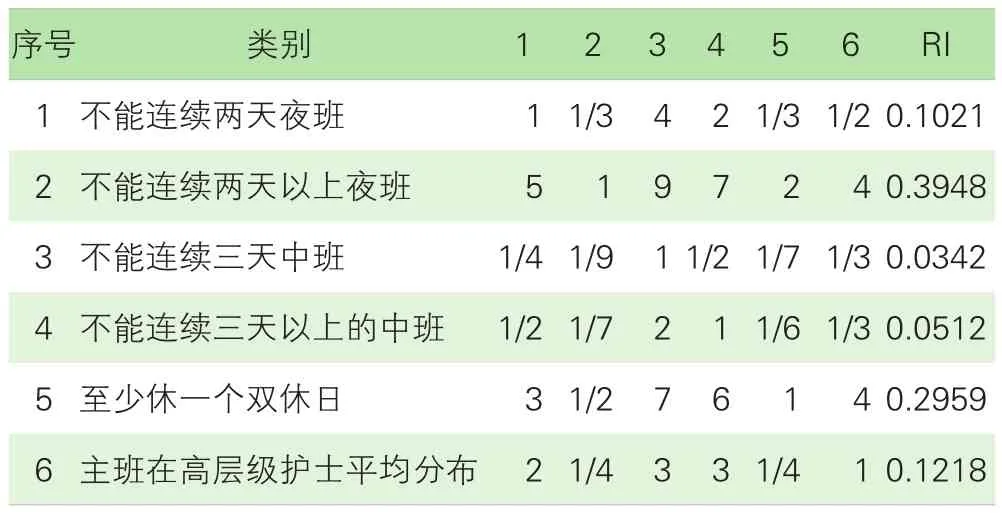
表4 判断矩阵和规则优先级

整数规划的目标函数

3.计算。这个调度模型共有4562个变量和3955个约束条件，用LINGO建模语言求解，运算结果函数的最小值为0.076，基于整数规划，除M3ij(6，17)=1外，其他的约束条件都能被满足，即i=6的护士在17、18、19三天连续值中班，违背了软约束条件3，需要这名护士做出让步，其余护士均满足了需求，是具有人性化的排班方案。

4.观察指标

4.1 护士对排班方案满意度，包括：合作满意度(3个条目)、工作量满意度(4个条目)、人性化需求满意度(3个条目)。以上三个维度的满意度评分按照Likert 10级评分法对每个条目分别进行评分后求和而得，每个条目计10分，得分范围是1～10分，1分为非常不满意，10分为非常满意。十点量表具有稳定的优越性，等级越多Likert评分法，鉴别力越高，所需样本量越少[7]。护士对排班方案满意度总评分计分方法为对上述三个维度的满意度评分进行求和。

4.2 医师对护理质量的评分，包括：技术规范(2个条目)、工作流程(4个条目)、应急处理(3个条目)、器械护士配合度(2个条目)、巡回护士配合度(2个条目)。以上五个维度的质量评分按照Likert 10级评分法对每个条目分别进行评分后求和而得，每个条目计10分，得分范围是1～10分，1分为非常不满意，10分为非常满意。采用匿名评分方式，医师对护理质量的评分总分计分方法为对上述五个维度的质量评分进行求和。

5.统计学方法。采用SPSS22.0软件对数据进行统计分析，计量资料用(均数±标准差)表示，采用t检验，以p＜0.05表示差异具有统计学意义。

结果

1.两组护士对排班方案满意度(合作满意度、工作量满意度、人性化需求满意度)，观察组高于对照组。见表5。注：p值为Sig.(双尾)检验

表5 护士对排班方案满意度(分，)

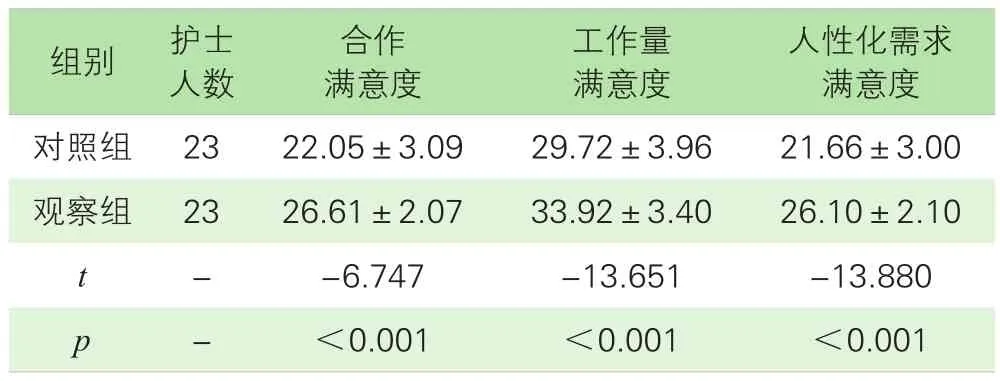
表5 护士对排班方案满意度(分，)

人性化需求满意度对照组 23 22.05±3.09 29.72±3.96 21.66±3.00观察组 23 26.61±2.07 33.92±3.40 26.10±2.10 t - -6.747 -13.651 -13.880 p - ＜0.001 ＜0.001 ＜0.001组别 护士人数合作满意度工作量满意度

表6 医生对护理质量评分(分，)

表6 医生对护理质量评分(分，)

注：p值为Sig.(双尾)检验

组别 医生人数 技术规范 工作流程 应急处理 器械护士配合度 巡回护士配合度对照组 147 13.80±1.80 28.80±2.68 20.91±2.49 14.06±1.68 13.98±1.68观察组 147 16.72±1.38 34.00±2.28 25.68±1.80 16.86±1.30 17.00±1.16 t--24.715 -17.462 -20.492 -18.194 -17.213 p-＜0.001 ＜0.001 ＜0.001 ＜0.001 ＜0.001

2.两组医生对护理质量评分(技术规范、工作流程、应急处理、器械护士配合度、巡回护士配合度)，观察组高于对照组。见表6。

讨论

手术室护士的工作压力和工作强度很大，在排班问题上有很多的限制条件，需要统筹权衡，才能有效地利用现有的人力资源，降低护士的职业倦怠感，保证手术质量，提高手术效率[8]。基于整数规划和变换规则优化算法的手术室护士排班模型能够显著提高护理服务质量，调整护士的精神状态，改进工作氛围、加强责任心和纪律性，具有重要的临床意义。

本研究结果显示，观察组护士对新的排班方案满意度(合作满意度、工作量满意度、人性化需求满意度)高于对照组，观察组医生对护理质量评分(技术规范、工作流程、应急处理、器械护士配合度、巡回护士配合度)高于对照组，说明基于整数规划和变换规则优化算法的手术室护士排班模型可以提高整体护理质量，提高工作效率和护士对排班方案满意度。

排班模型基于整数规划和变换规则优化算法，每个班次护理人数的需求是根据患者手术需求量预测得出，但是遇到急诊手术、外科会诊等临时手术需求，会加大工作负荷和人员需求，这时必须有后备的临床资源介入才能保证患者的突发病症得到及时治疗，排班模型的实施还需要修正变量以应对临时人员调配，这是此排班模型需要改进的地方。