基于核心素养下优化教学设计

唐红琳

【摘要】深入研究教材内容，从核心素养培养目标、GeoGebra的现场演示、学生分组合作研讨探究及课后阅读选做题等部分对《椭圆及其标准方程》这一课时的教学设计进行优化，设计课堂中问题解决的同时，把学生数学核心素养的培养作为重要内容。

【关键词】数学核心素养   GeoGebra   教学设计

【中图分类号】G633.6

【文献标识码】A

【文章编号】1992-7711（2020）31-160-02

在新教材新高考形势下，如何优化教学设计，怎样能够将学生数学核心素养的培养和教学实践结合在一起的相关问题越来越受到大家的关注。现在就如何优化人教A版选修2-1第二章中《椭圆及其标准方程》第一课时的教学设计，来展开我们的研究和思考。

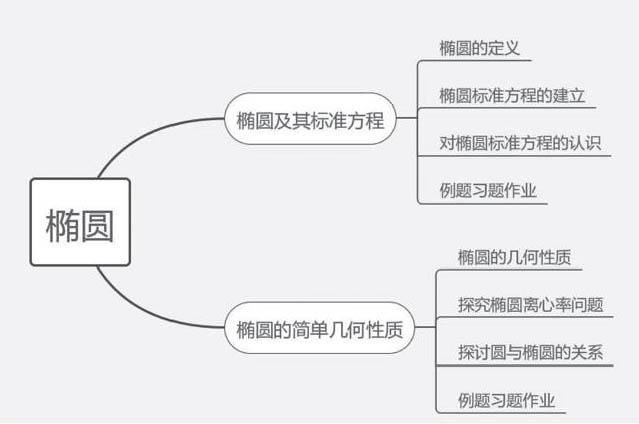
一、根据《2.2椭圆》本节知识结构思维导图（如下图），优化本节课的教学目标

（一）知识与技能

1.对椭圆的定义进行分析，理解椭圆的概念;

2.对关于椭圆的标准方程进行深入分析，对推导过程进行探索，对简单的问题进行解析的过程当中运用椭圆的定义。

（二）数学思考与问题解决

1.以天体运行截面与圆锥侧面的交线的演示，对抽象的数学印象以及数学思维方式进行培养;

2.在老师的引导下，让学生学会归纳椭圆定义，自行对标准方程进行推导，学会用数学的逻辑方式来解决问题;

3.在实践当中运用椭圆方程，学会数形结合，让学生学会分析和解决数学问题。

（三）情感与态度

1.在学习椭圆的画法的过程当中，提高学生的参与度，让学生能够通过实践运用更加深入的理解椭圆定义;

2.通过学习椭圆的相关知识，注重方法的传授，引导学生用数学的思维方式来解决问题，提高学生的数学学习兴趣，真正了解生活当中的数学应用。

二、针对教学活动实施的过程进行优化，体现于每部分的设计意图

（一）以学习内容为依据，进一步优化情境设置，让学生对所学内容更加感兴趣

在原有题材1和2的基础上，增加3，对圆锥曲线形成过程进行演示。

“1.神舟飞船在执行任务绕地球飞行时的轨道是什么图形：

2.太阳系内行星绕太阳转动时的轨道是什么图形：                     ”

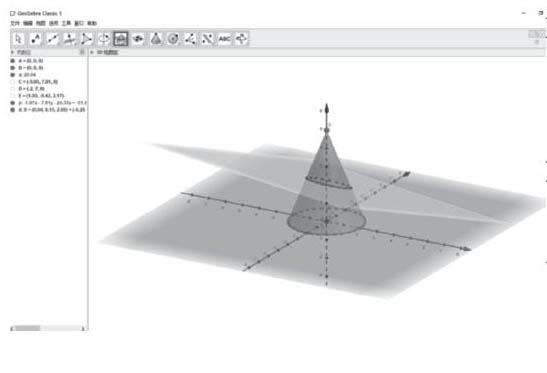
3.现场通过GGB演示用一个平面截取圆锥面，截口曲线的图形形状

设计意图：从熟悉的题材出发，引入问题，让学生能够体会到，在实践生活当中数学是如何进行应用的;通过实力的引入，导入主题，让学生初步认识圆锥曲线。（培养学生的数学思维能力和应用能力）

（二）针对课前探究、课上和课后思考進行优化

1.课前学生小组合作完成探究

准备一条无弹性细绳子和两个固定端.当套上自己的笔，拉紧绳子，移动笔尖，在本子上画出的图形是椭圆.

设计意图：通过小组内部的交流，对椭圆的一种画法进行认识，体会知识的形成过程，为上升到理论知识做准备。

2.优化课堂思考

思考1：观察在绘制椭圆时笔尖时怎样移动的？受到什么条件限制？

要想画出椭圆必须要满足什么条件呢？

思考2：观察以为焦点的椭圆上任意一点M，有什么性质？（引导出椭圆的定义）

课后思考3：回答以下两种情况下，M点的轨迹是什么？

（1）|MF1|+|MF2|=2a（2a=2c=|F1F2|）

（2）|MF1|+|MF2|=2a（2a<2c=|F1F2|）

设计意图：让学生自己独立思考，体会数学概念的严谨性，完善“常数”的必备条件（培养学生的数学抽象素养）

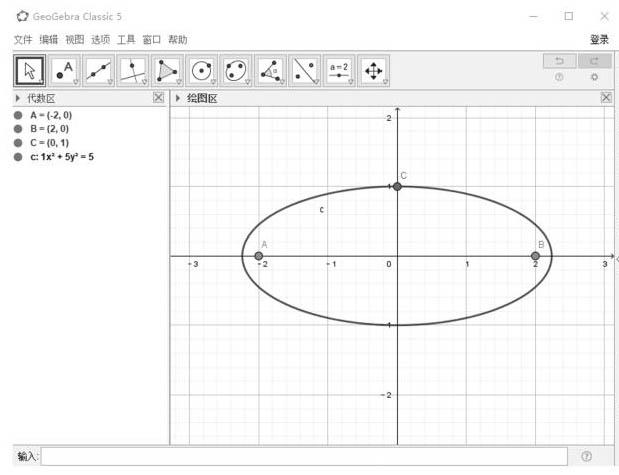
3.现场通过GGB演示绘制椭圆图形

设计意图：让学生积极参与、亲身经历椭圆的画法，加深对椭圆的理解（发展学                                   生数学抽象和直观想象素养）

（三）针对研讨探究过程进行优化，让学生全程参与，主动实践

1.探究1：针对椭圆图形，使用什么方法能求出其方程呢？怎样建系更方便呢？

2.探究2：以小组合作形式选定焦点在x轴和y轴上两种方案，由各组学生研讨完成推导过程（坐标法）。（对于在推导过程当中，学生遇到的困难进行关注并及时辅助解决）

3.探究3：在对标准方程进行解析的过程当中，你能总结出几条椭圆标准方程的特点呢？

设计意图：对于如何简化椭圆方程进行主动实践，获取知识。利用探究活动让学生学会合作解决数学问题，让学生全程参与数学坐标法的建立和方程推导的过程。（让学生拥有更强的逻辑推理能力）

（四）针对例题研讨进行优化，发展学生的数学建模素养

例1 求适合下列条件的椭圆的标准方程

（1）已知两个焦点F1、F2的坐标（-3，0）（下转第163页）（上接第160页），（3，0），椭圆上的点M到F1、F2距离和等于2  5 .

（2）已知椭圆经过点（  ，-  ）并且两个焦点的坐标分别是（0，-4），（0，4）。

例2 如图，圆心为（0，0），半径为1的圆O，过圆O上任意一点P向x轴作垂线段，求线段中点M的轨迹。

设计意图：让学生直接参与例题习题练习中，体会椭圆的标准方程特点及轨迹方程求解。（对学生的数学建模能力进行提升，发展学生的数学逻辑思维能力）

（五）针对评价小结及课后作业进行优化：

1.自我总结

（1）椭圆定义需要注意的条件是什么？

（2）经过哪几步能够完成椭圆标准方程的求解？

（3）是否掌握如何求动点的轨迹？

2.作业设置

必做题：课本第42页1、2、3、4。

阅读选做题：

流浪地球在上映以后，票房一直居高不下，深受大众的喜爱，假设木星是地球流浪轨迹的中心点，再不记地球半径的情况下，用质点P来表示地球，F表示木星。已知地球的近木星点A（轨道上到木星表面最近的点）离木星表面的距离为100万米，远木星点B（轨道上到木星表面最远的点）离木星表面的距离为2500万米。

要求同学们对该椭圆的标准方程进行求解，并尝试运用画图建立坐标系的方法来完成。

设计意图：及时让学生对本节课的所学进行总结，能优化学生的认知结构.课后作业的布置也以新高考的出题模式出现阅读选做题，让学生能够独立探索和解决问题（发展学生逻辑推理和数学建模、数据分析素养）

三、本节课课堂设计，从引入到作业布置，都设计了吸引学生的地方，比如用GGB绘制用一个平面截取圆锥面，截口曲线的图形形状;学生亲自画椭圆图形等，学生学习起来没那么枯燥，主要是为了提高学生的实践意识，通过亲自动手，主动学习，真正体现出学生在学习过程当中的主体地位，学会运用数学思想来思考问题，在推导和应用中，观察能力、运算能力、推理能力等得到训练，进一步提升学生的数学素养。

总之，教学要做到立德树人，必须要从数学核心素养的培养出发，教学中让数学知识的学习过程缓慢些，要有“三分教七分等”的心态，能够更好的帮助学生形成数学思维方式，我们在备课时一定要深入钻研教材内容，对数学学习的本质进行认识，根据每个学生不同的素质，因材施教，以学生为中心，开展教学活动，提高数学问题的合理性，对教学活动进行精心安排，让每一节课都能够体现出教师的用心，都能够起到对学生的数学核心素养进行提升的目的。

【参考文献】

[1]GeoGebra 5.0官网教程.https：//wiki.geogebra.org/zh/.

[2]中華人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018.

[3]顾广林.课堂教学中数学文化教育价值的挖掘[J].中国数学教育（初中版），2010（11）：2-5.