探讨中学物理求质心的方法

近年来，中学物理选拔赛或竞赛中常常出现求均匀物体的重心，严格来讲此处的重心是一种重力场平行且物体各个位置的引力大小g 相等的一种理想情况，此时物体的质量分布和物体的重力分布是一致的，物体的质心和重心位置重合，也就是求物体质心的问题。而中学阶段除非特别说明，都是基于这种理想状况下讨论物体的质心状况。

重心可以看着物体各部分所受重力的合力的作用点，重心是一个定点，一般物体可用悬挂法求的重心，但是悬挂法只适合实验性质的题解。规则物体可以采用诸如作图法以及加权平均法等多种方法求解。质心是物体(或物体系)的质量中心，在研究物体质心位置时，可将物体的质量看作集中于质心，某种意义上类似于重心的作用点。在理论上，质心是对物体的质量分布用“加权平均法”求出的平均中心。如图1 所示，三维空间中，物体系M 可等效划分为5 个质量各异或相同的小物体系mi。

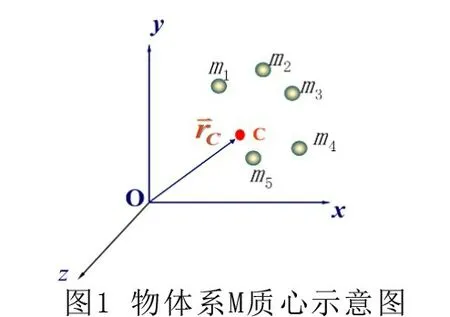
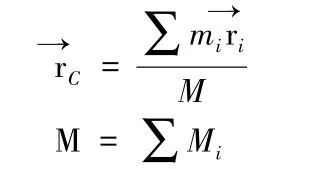
其中(1 ≤i≤5)

中学阶段尤其初中物理通常只需考虑平面坐标系中的(x c，yc)

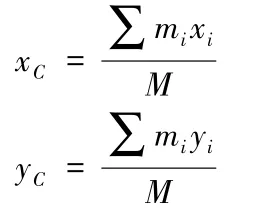
下面以实际质心(重心)问题例题解析提供多种解题方法。

一、用作图法求出均匀薄板的质心

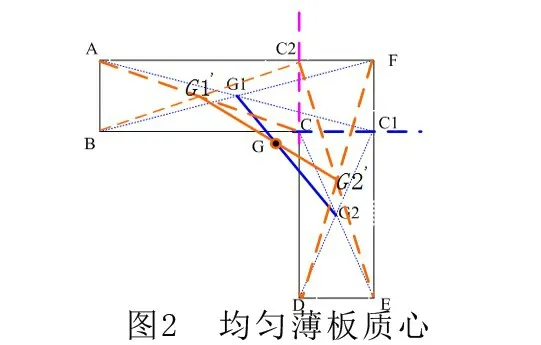
图2 中薄板可以看作ABC1F 和CDEC1 两块薄板拼接，因此可分别求二者质心分别为G1 和G2，同理也可以看作是ABCC2 和C2DEF 分别的质心G1'和G2'，则G1G2 与G1'G2'的交点G 即为该薄板的质心。该方法同样也适合更复杂的如Z 字形薄板的处理。此例也说明了物体的质心也可能不在物体上。

二、加权平均法求物体系质心

例 如图半径为R 的圆薄木板(厚度可忽略不计)，上面分别叠加了半径为R/2 以及R/4 的圆薄木板，求当前物体系的质心。

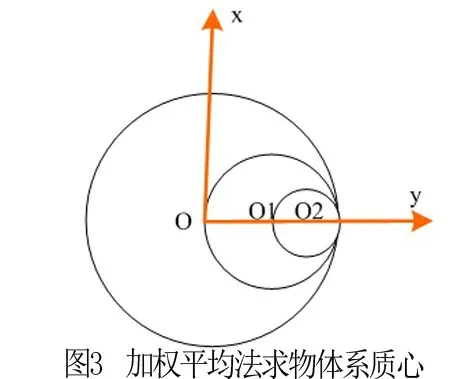
如图，以✍O 的圆心为原点建立坐标系，由于题中薄板厚度不计，因此只需考虑x，y 方向的质心坐标(x c，yc)，整个物体系基于y轴对称，所以yc=0

假设✍O 薄板的质量为M，则其余2 个分别为M/4 以及M/16

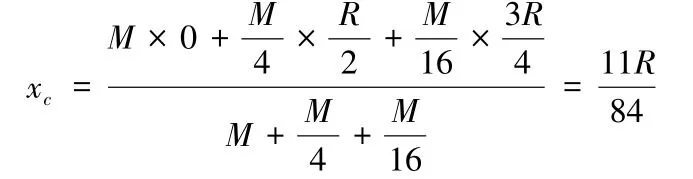
三、机械杠杆法求质心

例 如图4，半径R=30cm 的均匀圆板上挖出一个半径r=15cm的内切圆板，则剩余部分的重心离原来圆心的距离为多少?

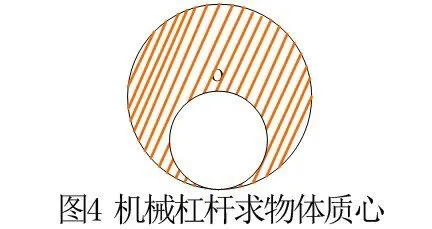
此题可假设没有挖孔时的状态，此时挖孔部分的重量和剩余部分的重量相对于大圆的圆心O 满足在Y 轴杠杆平衡，设完整的薄板重量为G，则剩余部分的重量为，那么杠杆平衡公式为

四、微元法积分方式求质心

对于质量连续分布的物体，可以采用微元法将物体分拆成多个规则形状，采用微积分方式处理，这块知识超越了中学范畴，可参考相关文献。