负压或真空条件下Ω形波纹管的强度计算公式研究

2020-11-18 10:55:50牛玉华吴建伏陈云飞

压力容器 2020年10期

关键词：弯曲应力波纹管计算公式

牛玉华，吴建伏，陈云飞，李扬

(1.南京晨光东螺波纹管有限公司，南京 211153；2.东南大学，南京 211189)

符号说明：

P——压力，MPa；

r——Ω型波纹管波纹的平均半径，mm;

n——多层波纹管中厚度为t的材料层数;

tp——波纹管中单层材料的实际厚度(即考虑到在成型过程中厚度减薄)，mm;

Dm——波纹管波纹的平均直径，mm;

Cp——在特定的设计计算中，使U型波纹管波纹段的性能相当于板条梁的修正系数;

rm——U型波纹管波纹的平均半径，mm;

w——Ω型波纹管波高，mm;

rit——Ω形波根部小圆弧内半径，mm。

0 引言

我国石化装备制造业经过多年的自行研制和引进吸收国外先进技术，已有了飞跃性的发展，大量原先需要进口的高温、高压及大口径的石化设备逐渐转为国产。为这些设备配套生产膨胀节的制造厂也需要设计、制造相应的高温、高压及大口径膨胀节。

膨胀节的结构形式较多，按其波纹管纵向截面内的波纹形状来分通常有U形、Ω形及S形等。在高温、高压及大口径条件下，Ω形波纹管通常是较好的选择，但这些石化设备常常需要按多工况设计，既要承受较高的内压，又要承受负压或真空。EJMA标准[1]提供了Ω形波纹管承受内压时的计算方法，但该标准明确说明受负压的Ω形波纹管不包含在标准中。目前国际上的其他波纹管膨胀节的设计标准和规范均未涉及受负压的Ω形波纹管的计算。

1 某国际项目Ω形波纹管失效案例

某国际项目的浮头式换热器采用了36 in(91.44 cm)Ω形波纹管膨胀节，按ASME规范[2]进行设计和制造。设计要求同时耐正压和负压5.0 MPa，按ASME规范内部和外部水压试验压力均为7.2 MPa。该产品按ASME规范设计和制造，出厂前按规范完成了内压试验，由于规范未规定Ω形波纹管的外压计算及压力试验要求，该产品出厂前未做外压试验。

产品交付用户之后，用户按换热器设计规定，分别进行了内压和外压试验，产品内压试验符合要求，但在进行外压试验时，打压到3.0 MPa时，Ω形波纹管膨胀节产品发生失效变形，如图1所示。通过对该产品的失效情况分析，判断为外压子午向弯曲应力过大引起的失效变形。因此，进行负压或真空条件下Ω形波纹管的强度和稳定性分析和验证，形成可靠的计算方法和公式，并纳入规范，已非常有必要。

图1 Ω形波纹管膨胀节失效变形情况

2 有关Ω形波纹管真空及负压下计算方法介绍

EJMA标准[1]提供的关于U形波纹管在负压下的计算方法，分两个部分的内容：U形波纹管在负压下的强度计算；U形波纹管在负压下的稳定性计算。EJMA标准提供了Ω形波纹管承受内压时的计算方法，但该标准明确说明受负压的Ω形波纹管不包含在标准中。目前国际上的其他波纹管膨胀节的设计标准和规范均未涉及受负压的Ω形波纹管的计算。

笔者已在文献[3]中对Ω形波纹管在负压或真空条件下的计算提供了计算方法。如图2，3所示，与U形波纹管的沿轴线对称形状不同，Ω形波纹管的形状沿轴线完全不对称，由Ω形波和直段组成。在进行负压计算时不能像U形波纹管可以直接用无增强型波纹管的计算公式直接进行强度计算，Ω形波纹管需要将Ω形波和直段分开进行考虑。文献[3]中分别对Ω形波纹管直边强度和稳定性计算[4]、Ω形波部分的强度计算进行分析及相关验证作了详细的描述。

图2 受负压的Ω形波纹管(外部加强环不起加强作用)结构示意

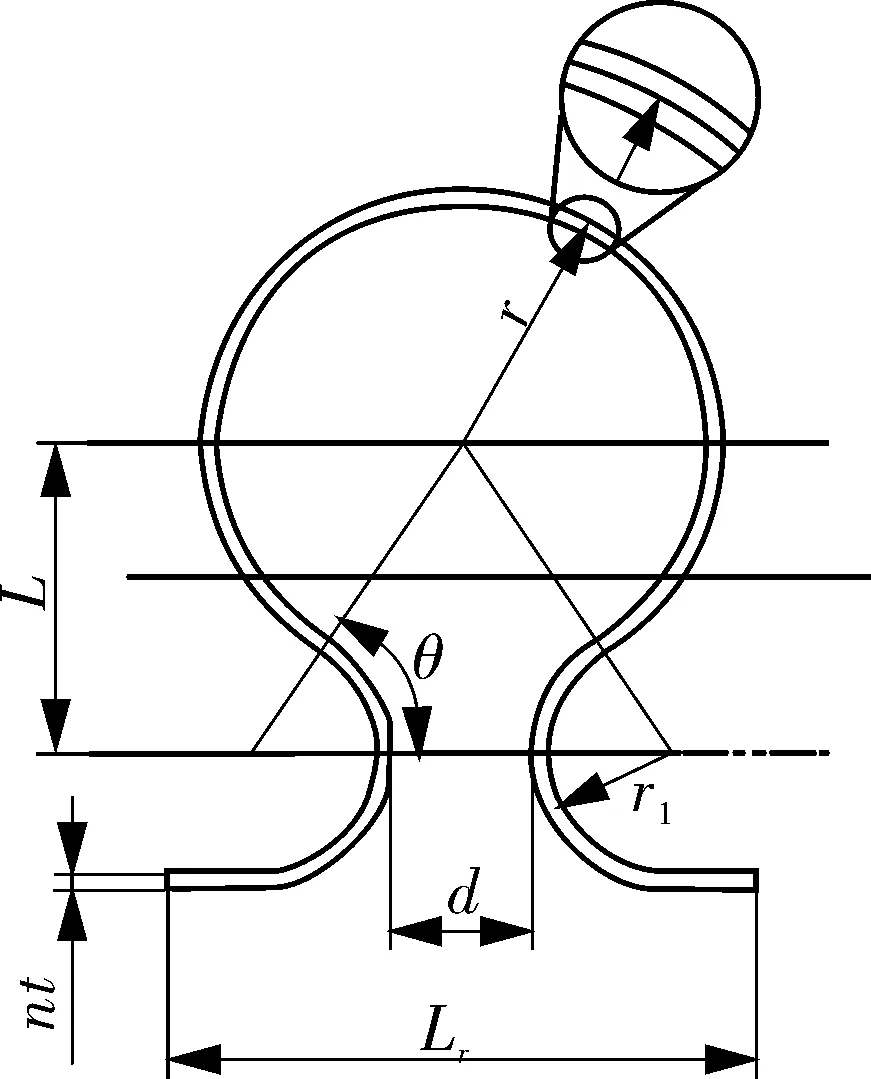
图3 受负压的Ω形波结构示意

关于Ω形波在负压或真空条件下的强度计算部分，文献[3]有如下计算公式。

(1)受负压时的Ω形波部分的周向薄膜应力的计算公式[5]。

(1)

(2)受负压时的Ω形波部分的子午向薄膜应力的计算公式[5]。

(2)

(3)受负压时的Ω形波部分的子午向弯曲应力的计算公式。

(3)

其中，决定系数Cp的两个相关参数C1和C2的计算公式如下：

(4)

(5)

考虑到Ω形波根部半径的影响，rm按下式计算：

(6)

关于Ω形波在负压或真空条件下的强度计算公式，由于Ω形波的周向薄膜应力和水平较低，该项应力不是影响Ω形波强度的主要因素，为了简化计算，文献[3]认为无需进行Ω形波的周向薄膜应力的校核。

文献[3]中参照无增强型U形波纹管的子午向弯曲应力的计算公式提出了Ω形波的子午向弯曲应力的计算公式，其中修正系数直接引用了U形波纹管的修正系数，对于较小口径的Ω形波计算结果有一定的精确度，基本可以参照使用；但随着Ω形波口径变大，精度降低，存在比较大的偏差。

3 Ω形波真空及负压下的强度计算公式

本文在文献[3]的研究基础上对Ω形波在负压或真空条件下的子午向薄膜应力和子午向弯曲应力的计算公式重新进行了推导，并通过有限元方法及试验验证相结合提出了以下的计算方法。

Ω形波在负压情况或真空条件下与内压情况下完全不同，外部加强环已失去加强的作用，按加强环作用下推导出来的内压情况下的Ω形波的计算公式已不能完全引用。负压或真空条件下时的Ω形波部分所受的应力与无增强型U形波纹管的应力情况有相似之处。

负压或真空条件下时的Ω形波中产生的子午向薄膜应力S3及子午向弯曲应力S4也可以根据平衡方程得出，简要的推导(以单层为例)如下。

将波峰、波谷分别视为两端固定的直梁(边界取为固定端是因为波峰与波谷处的位移和转角均为零)，A,B两点的距离为w(见图4)，单位宽度上的板厚为tp，其上有均布载荷P的作用，其最大弯矩Mmax发生在A,B两点，即：

RA=RB=pw/2

(7)

MA=MB=pw2/12

(8)

外压在Ω形波中产生的子午向薄膜应力S3：

(9)

图4 Ω形波纹管简化为直梁示意

外压在Ω形波中产生的子午向弯曲应力S4：

S4=Mmax/W

(10)

式中W——抗弯界面系数。

将截面看成是高为tp，宽为1的矩形，则：

(11)

所以得：

(12)

与U形波纹管类似，在推导Ω波的子午向弯曲应力时，将波纹管简化为一个直梁，这与实际情况有着很大的差别，需要加一个修正系数K。

(13)

4 Ω形波子午向弯曲应力S4公式中系数K的取值

由于篇幅所限，关于修正系数K的计算数据和试验数据的验证及修正系数K的确定，将在另文详细描述。本文主要引用该文修正系数K的计算结果，如图5所示。

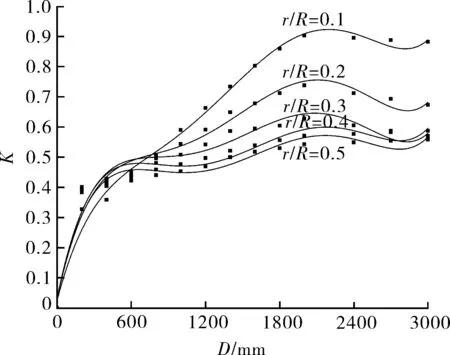
图5 修正系数K值的拟合曲线

5 Ω形波子午向弯曲应力强度计算结果与有限元分析结果对比

本文通过1种波形、3种口径Ω形波的有限元分析子午向应力结果[6]与采用式(2)和式(3)(采用Cp系数修正)及采用式(9)和式(13)(采用K系数修正)的子午向应力的计算结果进行对比。有限元分析对比的参数见表1。

表1 有限元分析对比的参数

从图6～8计算结果对比可以看出，采用式(9)和式(13)(采用K系数修正)的子午向应力的计算结果与有限元分析的结果一致性较好，但结果偏小一些;采用式(2)和式(3)(采用Cp系数修正)的子午向应力的计算结果与有限元分析的结果相比，在Ω形波口径较小的时候一致性较好且结果比较保守，但随着Ω形波口径加大，数据误差加大，出现较大的偏离[7-9]。