高温合金Inconel 617B的热变形及动态再结晶行为

罗 锐，陈乐利，程晓农，杨玉艳，袁 飞，崔树刚，张肖佩佩，曹 赟，刘 天，高 佩

(1.江苏大学 材料科学与工程学院，江苏镇江 212013；2.江苏银环精密钢管有限公司，江苏宜兴 214203)

0 引言

高温合金Inconel 617B是在Inconel 617基础上加入微量B元素而得到的Co-Mo固溶强化奥氏体合金[1]，具有优异的高温强度、高温抗氧化性能和高温耐腐蚀性能，在700 ℃时其高温蠕变强度约为Inconel 617的1.25倍[2]，因而被列为制造第四代核能系统高温气冷堆中热交换器的关键候选材料[3]。由于Inconel 617B没有固态相变，因而热变形成为控制其微观组织、优化其服役性能的关键手段。然而，国内外现阶段对该合金的研究集中在蠕变性能、抗氧化性能、析出行为等领域[4-8]，与热变形相关的研究却鲜有报道。

揭示材料在热加工过程中的变形特性及其本构关系是研究材料热变形行为的基础。因此，构建高温合金Inconel 617B的真应力-真应变曲线及高温本构模型具有重要意义。唯象型Arrhenius本构模型可有效描述变形参数与变形抗力之间的关系，被广泛用于构建高温合金[9]、不锈钢[10]、铝合金[11]等典型金属材料的本构关系。此外，动态再结晶(Dynamic Recrystallization,DRX)是高温合金热变形过程中细化晶粒、改善性能的有效手段[12]。确定材料发生DRX的临界变形条件具有重要的工程与学术价值。Jonas等[13]认为，材料发生DRX的临界应变可通过加工硬化率曲线的拐点获得，该理论已成功用于高温合金[14]、镁合金[15]等金属材料的临界再结晶预测。DRX发生后，不同变形参数对其动力学过程具有显著影响，构建Avrami动力学模型[16]有助于揭示金属材料的DRX演变规律[17-18]。朱怀沈等[19-20]研究了617合金的再结晶行为，并建立了动态再结晶方程，且杨康等[20]给出了合金的再结晶动力学曲线，这对研究617B合金的动态再结晶行为具有重要的参考价值。

本文基于先进的Gleeble热模拟技术系统，研究高温合金Inconel 617B的热变形及再结晶行为，绘制该合金的真应力-真应变曲线，建立Arrhenius高温本构模型，用以描述变形参数对流变应力的影响规律；基于Poliak-Jonas 理论，研究该合金的临界DRX条件，明确不同变形温度及速率下临界变形量的演变特点；构建高温合金Inconel 617B动态再结晶Avrami动力学模型，揭示其动态再结晶随应变的发展进程及形核机制，为其在第四代核电等领域的应用奠定理论基础。

1 试验材料与方法

本研究试验材料为Inconel 617B高温合金(热轧+固溶态)，其化学成分见表1。其原始组织如图1所示。

表1 高温合金Inconel 617B的化学成分 %

图1 Inconel 617B的原始金相组织

将合金加工为∅8 mm×12 mm的圆柱试样，利用Gleeble-3500型热力模拟试验机进行单道次等温压缩试验。试验参数为：变形温度950～1 200 ℃(以50 ℃为间隔)，应变速率0.01～5 s-1，真应变0.8。压缩前，在试样与夹头间加一层厚度0.05 mm的钽片，并将K型热电偶焊于试样表面以检测温度。以10 ℃/s的速率将试样升温至预设的热变形温度，保温30 s后进行恒温恒应变速率的热压缩变形。压缩完成后立即将试样进行气淬、水淬。基于计算机自动采集的压缩数据，绘制Inconel 617B合金的真应力-真应变曲线，构建Arrhenius本构模型以及动态再结晶动力学模型。

2 结果与讨论

2.1 流变应力特征

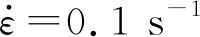
图2 Inconel 617B在不同变形参数下的真应力-真应变曲线

2.2 Arrhenius本构方程的构建

Sellars等[21]提出了一种Arrhenius型双曲正弦本构方程，以描述金属材料在热变形过程中的变形抗力与变形参数之间的关系，根据不同变形条件有3种表达式：

(1)

A1,n,α——材料常数；

σ——形变抗力，MPa；

Q——材料热变形激活能，kJ/mol；

R——理想气体常数，J/(mol·K)；

T——变形温度，K。

(2)

式中A2,β——材料常数。

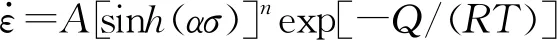
(3)

式中A——材料常数；

n——材料表观应力指数。

3种表达式中，通常选用式(3)来描述材料的热变形特性。

×exp(-56996.27/T)

(4)

(a)n1=6.891 3

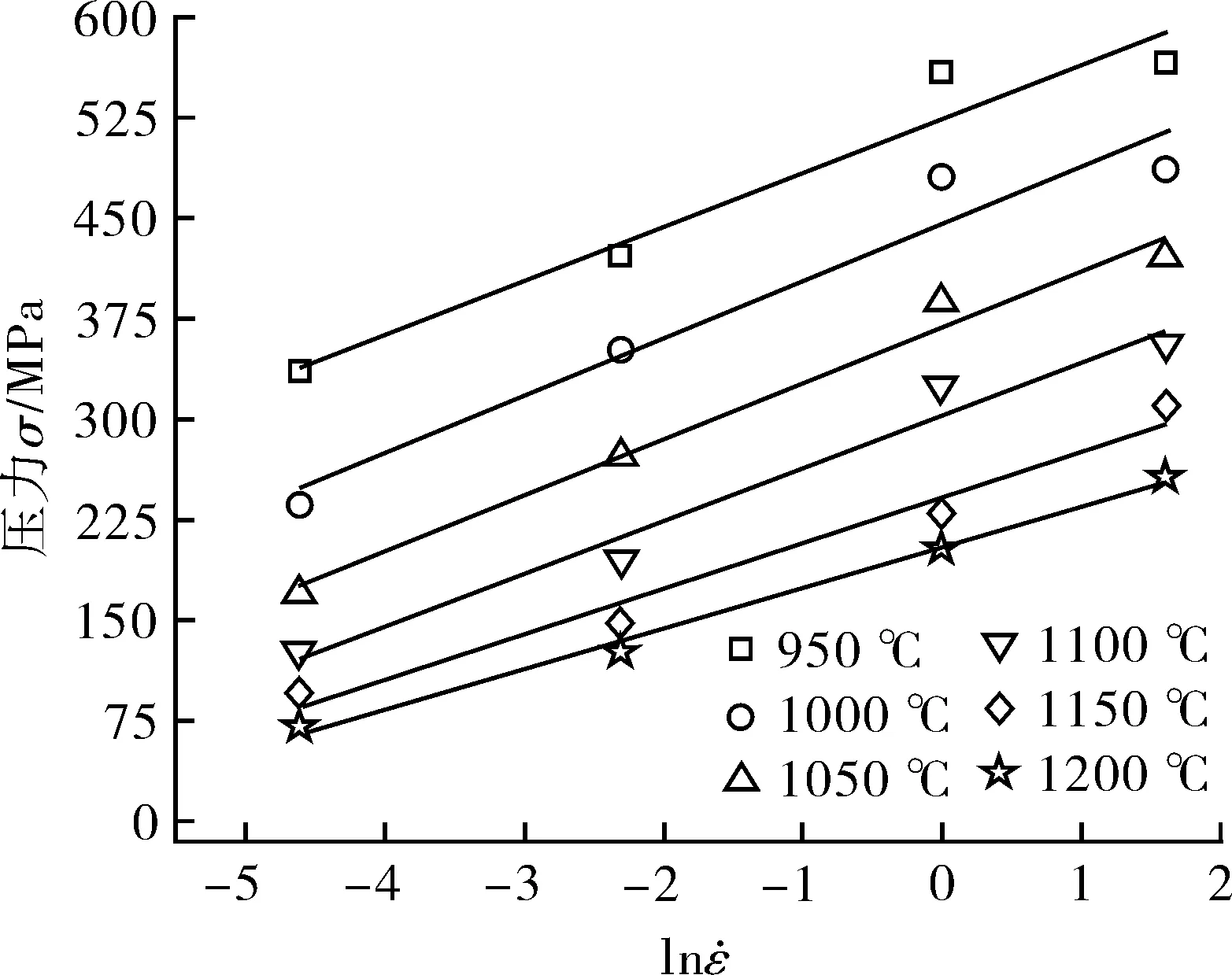
(b)β=0.026 6

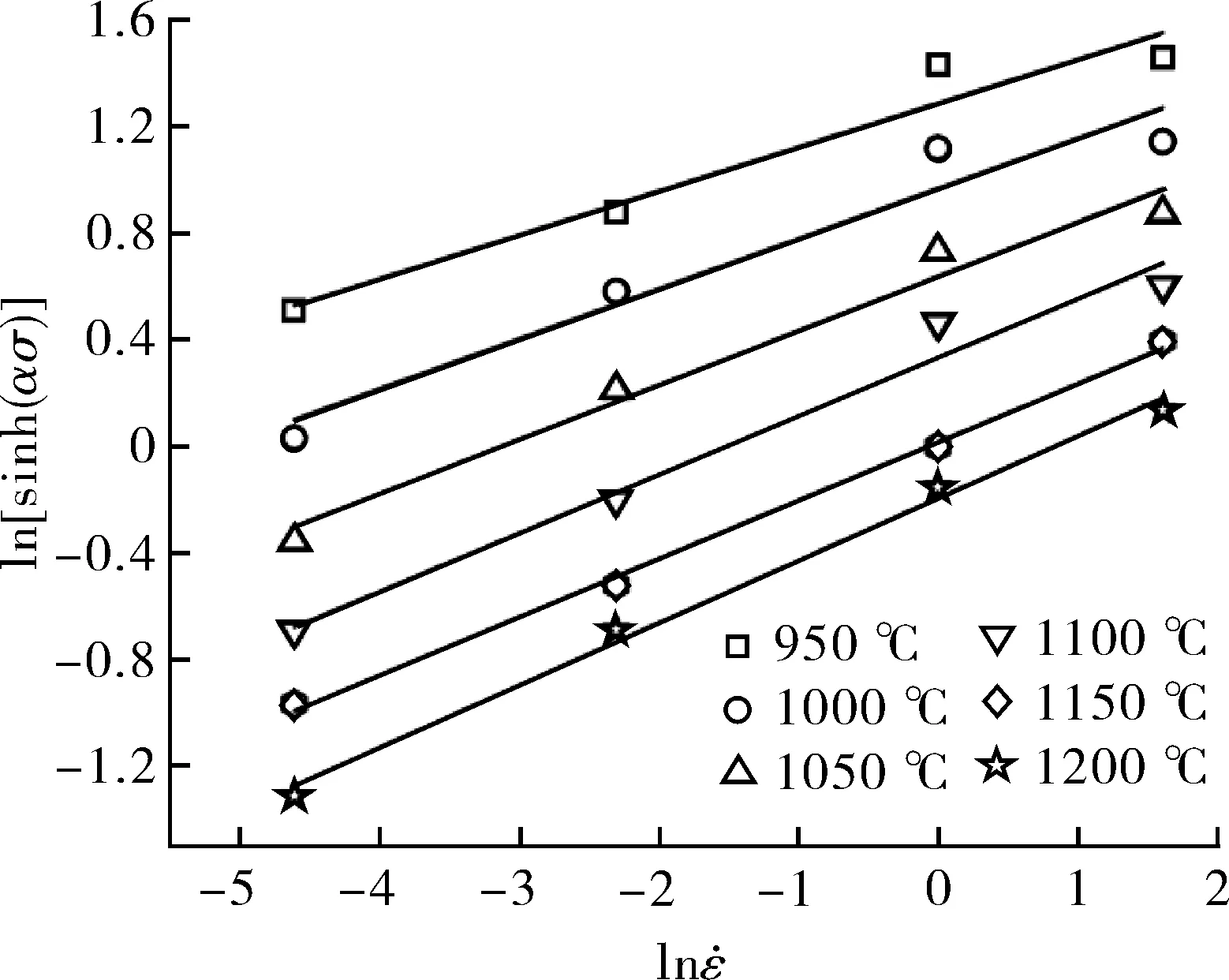
(c)n=4.948 8

(d)Q=473.867 kJ/mol

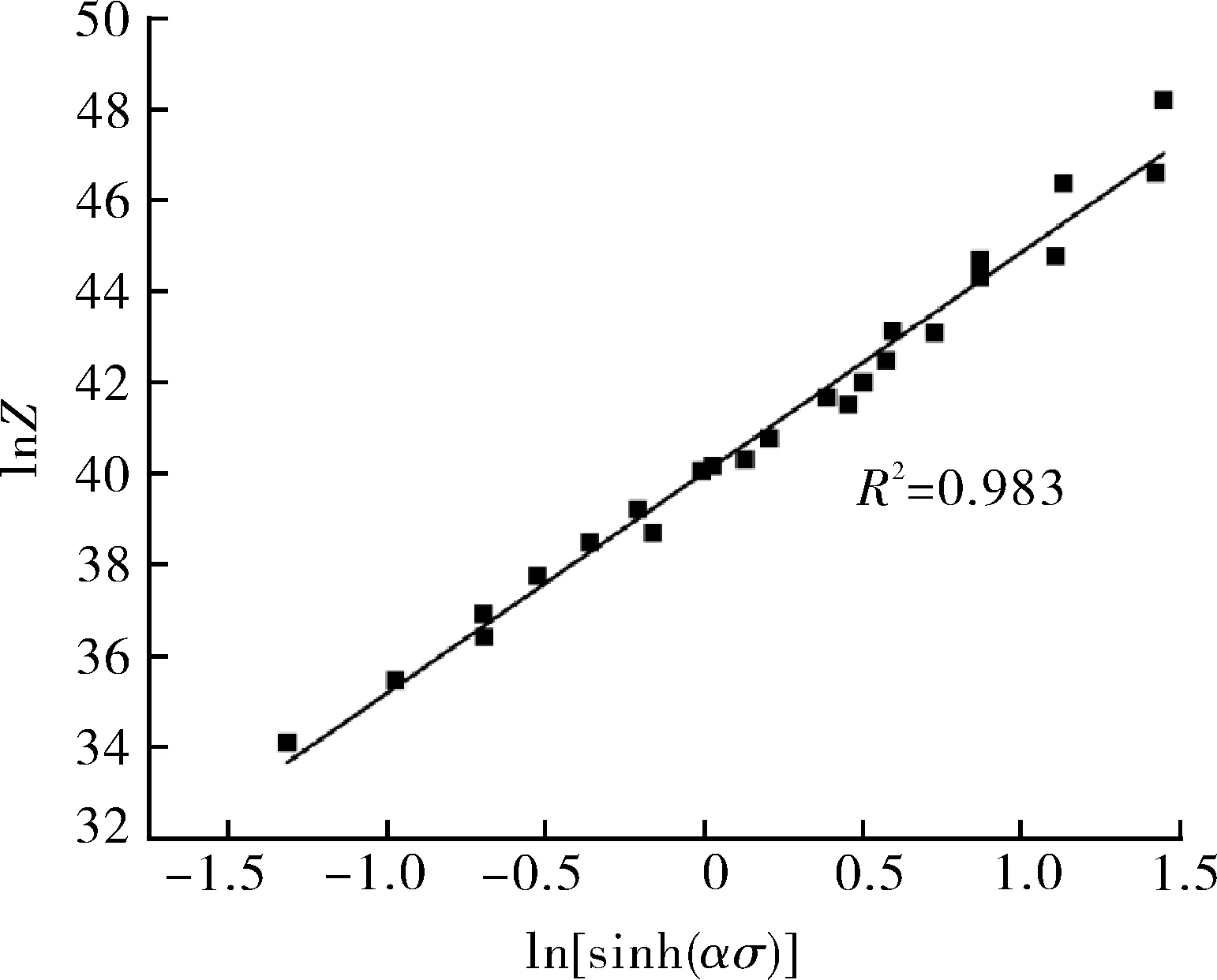
(e)lnA=39.992 1

2.3 动态再结晶动力学模型的构建

2.3.1 临界DRX模型的构建

材料在热加工过程中，变形导致位错增殖，引起加工硬化，同时材料内部的形变储存能增加。当变形量增大到某一临界点时，形变储存能达到阈值，会驱动DRX发生，产生动态软化效应，因而确定DRX的临界点对热加工工艺的制定具有重要的指导意义。Jonas等[13]认为，材料在峰值应力出现前，真应变(ε)与加工硬化率(θ，θ=dσ/dε)的三次多项式拟合曲线的拐点对应发生动态再结晶的临界条件，表达式如下：

θ=Aε3+Bε2+Cε+D

(5)

式中A,B,C,D——给定变形条件下的常数；

ε——真应变。

经试验发现，lnθ-ε和θ-ε的拐点意义相同，且前者绘图后拐点更为清晰。图4示出高温合金Inconel 617B在不同变形条件下的的lnθ-ε三次多项式拟合曲线，均呈现动态软化特征。在变形初期，动态回复出现，加工硬化率随真应变的增加线性递减；随后，曲线出现了明显的拐点，表明DRX开始出现，拐点横坐标即为材料的临界应变量；此后DRX迅速发展，软化效应大幅提升，引起加工硬化率的加速下降。

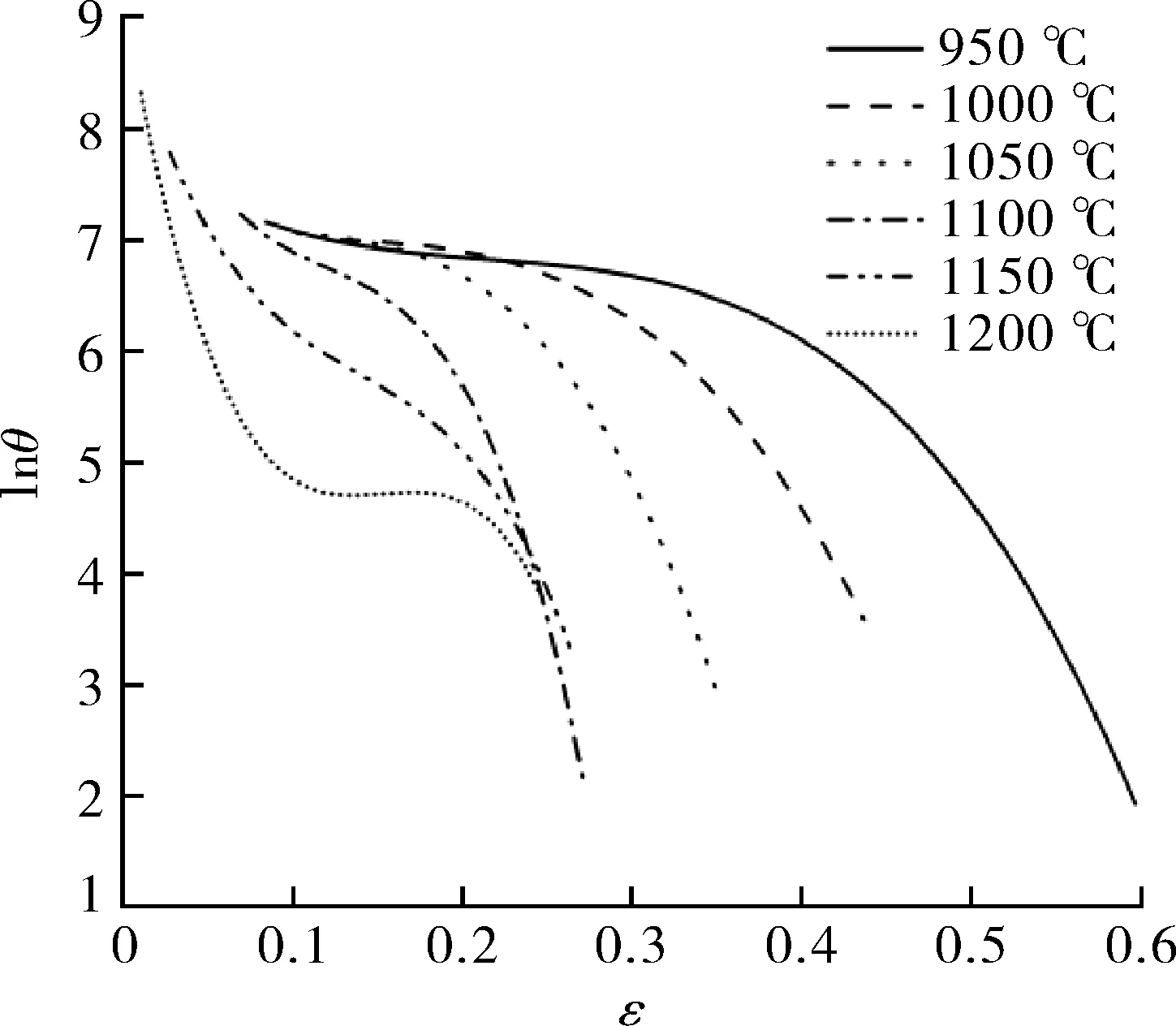
图5为Inconel 617B在不同变形条件下的(-dlnθ/dε)-ε关系曲线，曲线的最小值点对应lnθ-ε三次多项式拟合曲线的拐点，也即材料的临界应变点。通过(-dlnθ/dε)-ε关系曲线可更为准确地确定DRX临界条件，以便分析其变化规律。随着变形温度的降低和变形速率的增加，Inconel 617B的临界应变点呈现增大的趋势，这意味着在高温或低应变速率下更容易发生DRX。

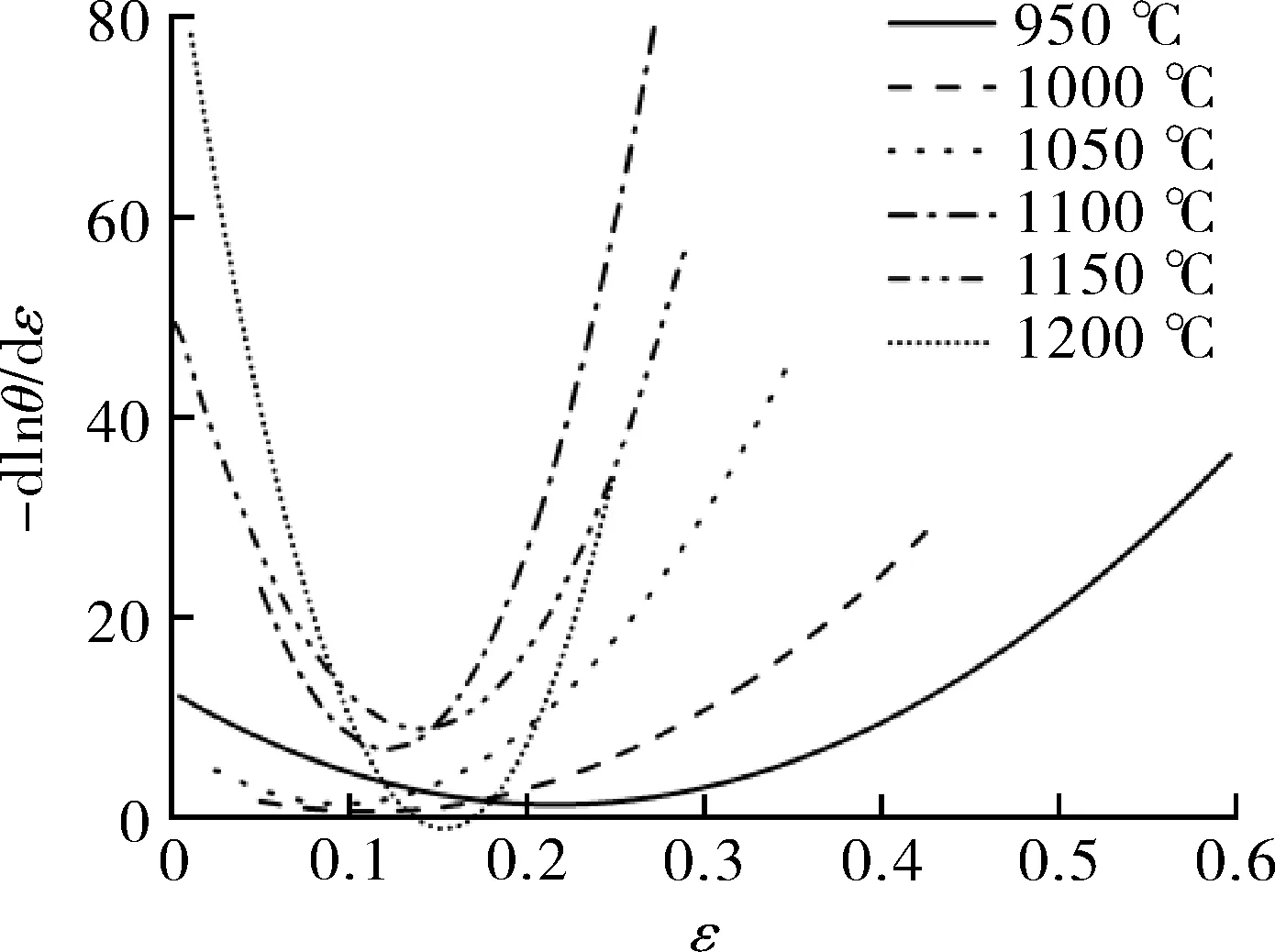
图5 Inconel 617B的(-dlnθ/dε)-ε关系曲线

有学者[14]证实金属材料DRX的临界应变与峰值应变呈线性关系。图6(a)为Inconel 617B的εc-εp线性拟合图，拟合相关性为97.8%，临界应变与峰值应变几乎呈正比例关系，其关系式如下：

εc=0.524εp

(6)

式中εc——临界应变；

εp——峰值应变。

Z参数可用于描述金属材料的临界DRX行为，Inconel 617B的Z参数在上文已确定：

(7)

图6(b)为Inconel 617B的εc-lnZ线性拟合图，拟合相关性达94.6%，临界应变与Z参数呈现较好的线性关系，如式(8)所示。通过式(6)和式(8)可有效预测不同变形参数下Inconel 617B的临界DRX条件。

εc=0.207lnZ-10.464

(8)

(a)εc - εp拟合 (b)εc- lnZ拟合

2.3.2 DRX动力学

构建Inconel 617B的动态再结晶动力学模型是揭示其DRX特性的有效手段，可预测该合金在不同变形量下发生DRX的程度以及DRX的形核特点[16]。一般来说，金属材料在热变形过程中的DRX行为遵循Avrami定律：

(9)

式中XDRX——材料发生DRX的程度；

k，m——Avrami参数，由材料成分及变形参数决定。

有研究[20]表明，当DRX作为材料热变形过程中的软化机制时，XDRX与变形抗力的变化直接相关：

(10)

式中σp——峰值应力，MPa；

σ——材料在热变形过程中的瞬时变形抗力，MPa；

σss——稳态应力，MPa。

以上数据均可通过热压缩试验获得。

将式(10)代入式(9)，并对所得方程的两侧取自然对数，可得：

(11)

将ln[-ln(1-XDRX)]与ln[(ε-εc)/εp]进行线性拟合，则lnk和m分别表示拟合直线的截距和斜率，得到k和m的值，进而确定材料的Avrami方程。

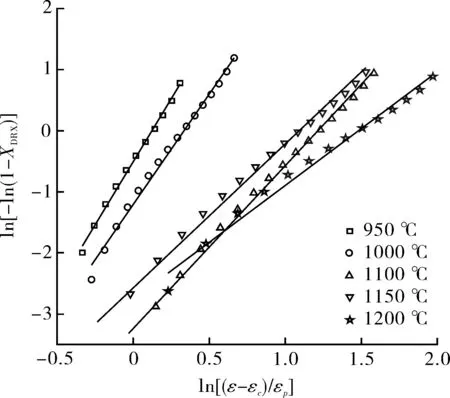
图7 不同变形条件下的ln[-ln(1-XDRX)]与ln[(ε-εc)/εp]拟合曲线

图7示出不同变形条件下的ln[-ln(1-XDRX)]与ln[(ε-εc)/εp]拟合曲线，将所有直线的截距和斜率取均值，即可得到k和m的值分别为0.185，2.91，则Inconel 617B的Avrami方程为：

(12)

文献[23]表明，当m的值介于1～3之间时，材料的主要DRX形核点是原始晶界，伴随链状组织的产生。Inconel 617B的m值为2.91，这意味

着在试验参数范围内，原始奥氏体晶界是其DRX的主要形核点，DDRX是该合金的主要DRX形核机制。

基于式(12)，计算出Inconel 617B在不同变形参数下的动态再结晶程度，并绘制Avrami曲线，如图8所示。随着应变的增加，DRX程度呈S形从0增加至1，且变形温度越高、变形速率越小，则DRX的孕育期越短，完成DRX所需的应变量也越小，因此，提高变形温度或减小变形速率有利于促进Inconel 617B的DRX行为。

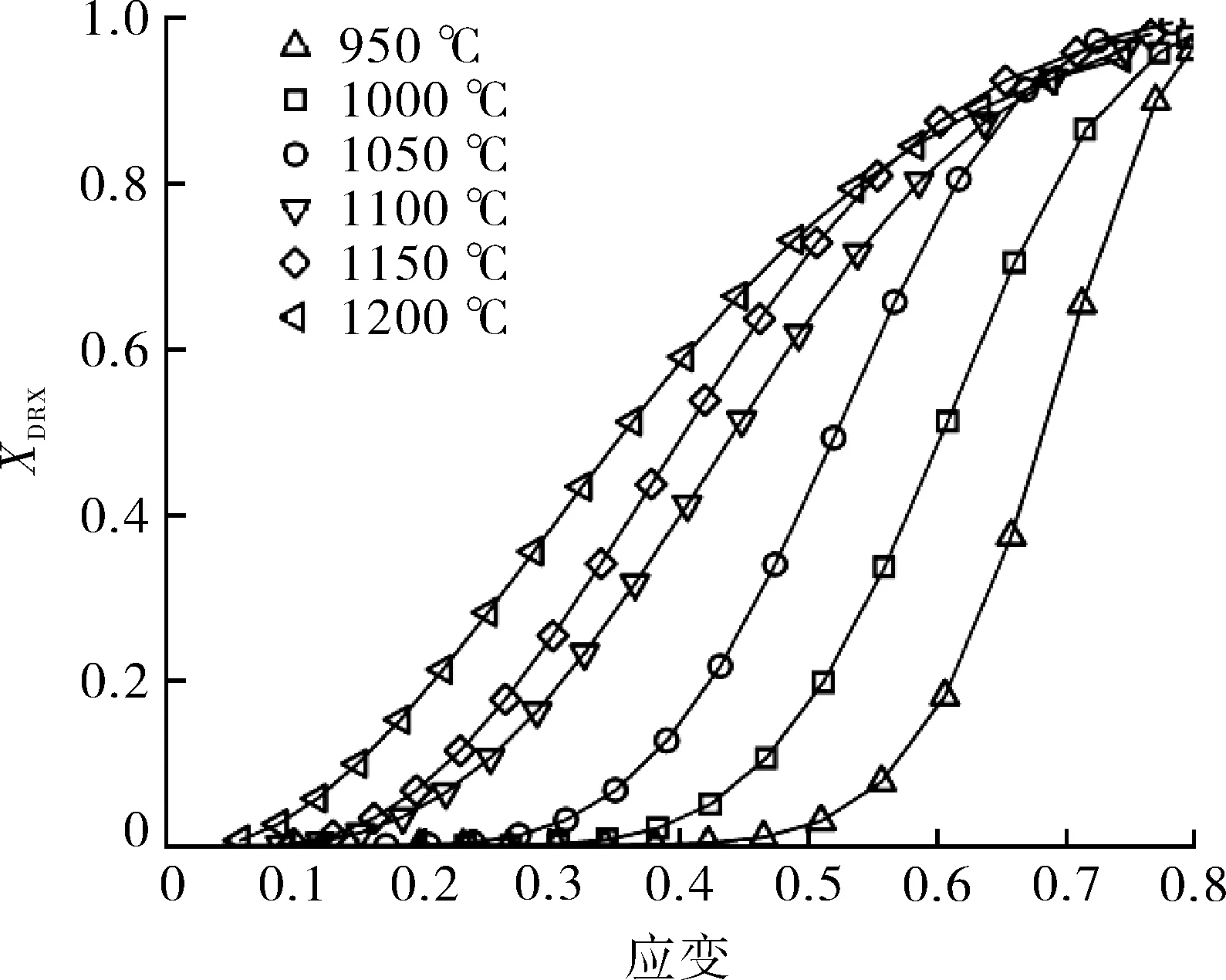
图8 不同变形条件下的Avrami曲线

3 结论

(1)通过Gleeble热压缩试验，研究了高温合金Inconel 617B在变形温度950～1 200 ℃，变形速率0.01～5 s-1条件下的热加工特性，真应力-真应变曲线表明，热变形抗力随变形温度的升高和应变速率的降低而显著减小，且曲线均呈现动态再结晶特征。

(2)构建了Inconel 617B基于峰值应力的Arrhenius本构模型，用以预测不同变形参数下的变形抗力，本构参数n表明在热变形过程中发生了位错攀移现象，热变形激活能Q确定为473.867 kJ/mol，进而确定Z参数(见式(7))。

(3)基于Avrami理论确定了Inconel 617B的临界DRX条件，DRX临界应变随变形温度的升高和变形速率的降低而减小，峰值应变与临界应变、Z参数与临界应变的线性拟合优度分别为97.8%和94.6%。

(4)建立了Inconel 617B的DRX动力学模型，变形温度越高、变形速率越小，则DRX的孕育期越短，完成DRX所需的应变量也越小。在试验参数范围内，原始奥氏体晶界是发生DRX的主要形核点，且以DDRX为主导。