压电执行器非对称磁滞动态建模和辨识
王 彭,宋克非,张佩杰,韩振伟,陈 波
(中国科学院长春光学精密机械与物理研究所,吉林长春 130033)
0 引言
压电执行器因其高分辨率、高致动力和高带宽而被广泛应用于精密定位系统,在扫描显微镜、自适应光学、半导体加工等领域有重要的应用[1]。这些应用领域大多需要较高的工作带宽和跟踪精度,然而受到压电材料固有的蠕变、迟滞特性[2]以及机电系统的动态特性影响,动态跟踪定位系统工作带宽和跟踪精度都受到了很大限制[3],同时由于蠕变和迟滞的非线性特征,还可能造成闭环控制系统的不稳定,对整个跟踪定位系统造成破坏性影响。
为了提高跟踪精度,补偿磁滞动态特性带来的影响,基于磁滞动态模型的前馈控制是一种常用的控制方法[4]。前馈控制器设计需要建立压电执行器的准确系统模型,然后基于系统的逆模型设计前馈控制器,从而线性化整个系统的响应。因此,在前馈控制器设计中,准确构建压电执行器系统模型是提高系统跟踪定位精度的关键。然而,压电执行器系统由线性动态特性、磁滞和蠕变等特性耦合而成,且线性动态特性既包含电路的动态特性,也包含机械系统的动态特性,这些部分的耦合造成了系统建模和辨识的困难,目前,对于动态特性和磁滞特性的耦合多采用分步辨识的方法[5]。磁滞模型是压电执行器系统模型的关键,主要分为两大类:一类是基于微分方程的磁滞模型,包括Duhem模型、Backlash-like 模型、Boue-Wen模型[6]等;另一类是基于算子的磁滞模型包括Preisach模型、Krasnosel’skii-Pokrovskii(KP)模型、Prandtl-Ishlinskii(PI)模型和Maxwell-Slip模型等[7]。基于算子的磁滞模型能精确描述大小滞环,且方便求解逆模型,在前馈控制中有较广泛应用。
本文根据压电执行器的组成,构建了系统各部分的模型结构,对系统的电路、机械和磁滞特性进行分离建模和辨识。首先利用方波小信号对系统电路和机械特性进行辨识,得到系统的线性动态特性,然后利用改进的PI磁滞模型对压电材料的磁滞特性进行建模,在线性动态模型的基础上对磁滞模型进行辨识。最后,以P841.1压电执行器为实验平台,对基于改进PI模型的磁滞动态模型进行了实验验证。
1 压电执行器系统模型
从物理结构上压电执行器系统可以分解为驱动电路、压电材料和机械结构。为了准确描述系统的动态特性,系统模型构成需要综合考虑各部分结构的特性。根据系统的物理组成构建了如图1所示的级联模型,其中,电路和机械结构部分采用线性传递函数表征,压电材料特性采用基于改进PI模型的磁滞模型表征。
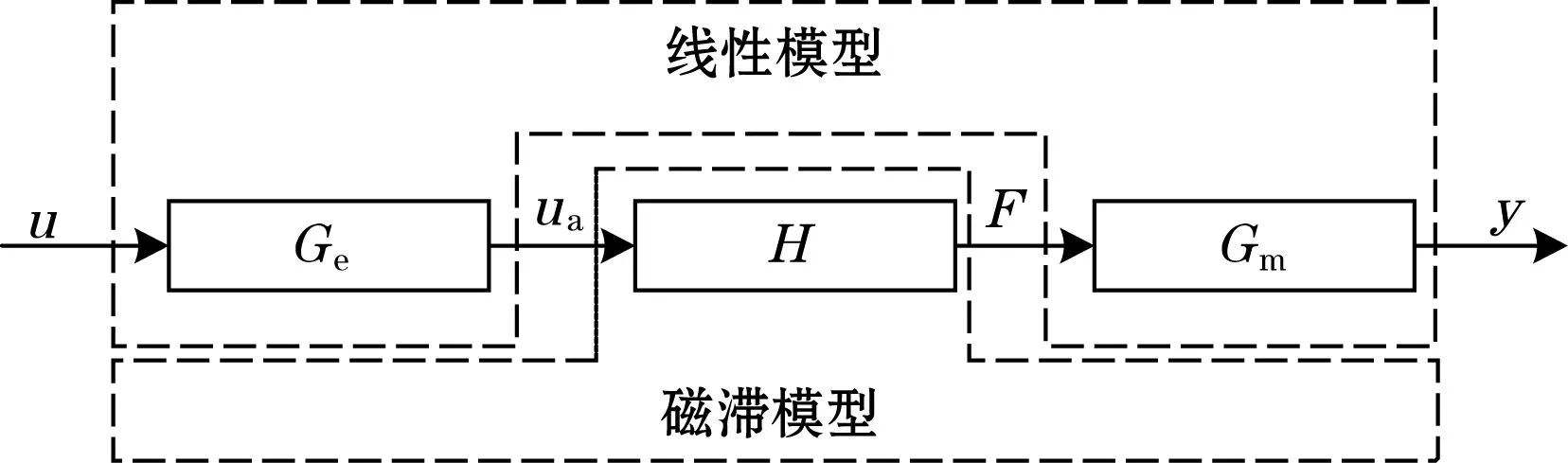
图1 级联系统模型
图1中Ge表示电路的传递函数;H表示压电陶瓷的磁滞模型;Gm表示机械结构的传递函数;u为驱动电路的输入电压;ua为驱动电路的放大输出电压;F为压电材料的输出力,同时为磁滞特性的输出;y为压电执行器的最终输出位移。上述变量中除F为不可测量外,其他量均为可测量。
1.1 驱动电路模型
压电材料在电路上可以近似表示为一个电容器,电荷型压电驱动电路可以部分克服磁滞和蠕变的影响,但是其电路较复杂且造价较高,所以现在较为常用的驱动电路为电压反馈型放大电路。由于驱动电路有一定的输出阻抗,并且压电负载为容性负载,因此,这两部分构成了一阶低通电路,如图 2所示,该模型忽视了直接压电效应。

图2 驱动电路及压电负载电特性
图2中R为驱动电路输出电阻;C为压电负载的等效电容;kamp为驱动电路放大倍数。该电路的传递函数形式如式(1)所示。

(1)
1.2 磁滞模型
传统PI模型是被广泛应用的基于算子的磁滞模型,PI模型利用算子的加权和以及输入信号的线性函数表征磁滞非线性,能够描述对称和率无关的磁滞特性。PI模型的算子主要有两种:Stop算子和Play算子,本文采用Play算子作为PI模型磁滞算子。Play算子为率无关算子,即算子的输出仅取决于当前输入和历史输入极值点,而与输入信号的频率无关,同时Play算子也是对称算子。假设输入函数v(t)在分段子区间[ti,ti+1]上单调连续,则Play算子[8]可以表示为
F[v](0)=fr(v(0),0)
F[v](t)=fr(v(t),Fr[v](ti))
(2)
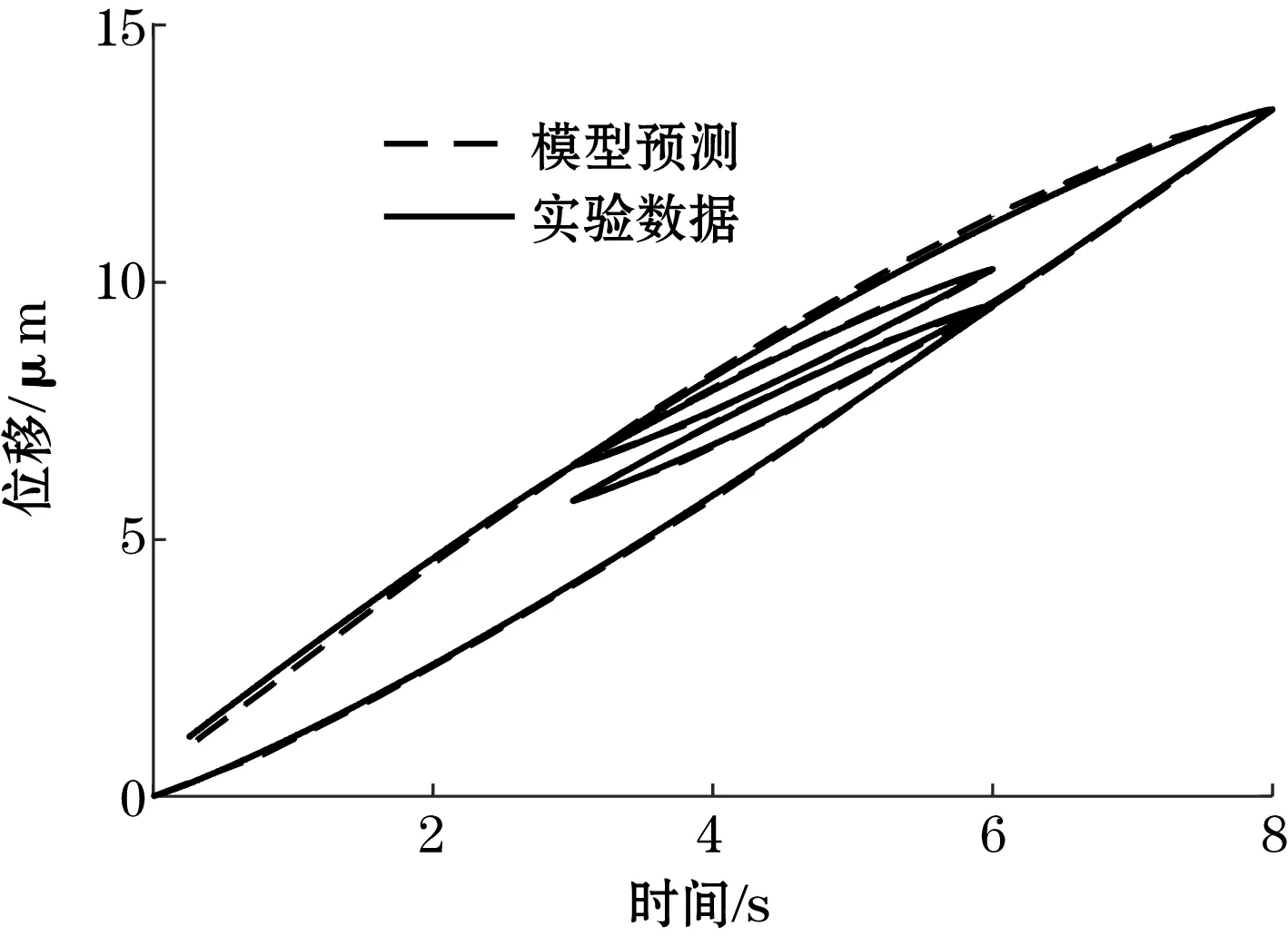
其中,ti fr(v,w)=max(v-r,min(v+r,w)) (3) 输出yp和输入v(t)的关系如下 (4) 式中:q为正常数;p(r)为算子的密度函数;R通常取到无穷大以保证积分的收敛性;密度函数可通过实验数据辨识得到。 因为传统PI算子的对称性,所以传统PI模型只能表征对称的磁滞模型,然而压电材料的磁滞特性是非对称的,因此,很多学者提出了改进的PI模型以表征压电材料的非对称特性[9-10]。在文献[4]的基础上提出了一种改进的PI模型,其基础算子如式(5)和式(6)所示,改进的PI基础算子增加了参数η,使基础算子拥有了非对称特性,可以表征非对称磁滞模型。 Fmr[v](0)=fmr(v(0),0) (5) 其中,ti fmr(v,w)=max(v-r,min(v+ηr,ω)) (6) (7) 改进PI模型的输出ym和输入v(t)的关系如式(7)所示,与传统PI模型相比,模型的第一项从输入函数的一次函数,修改为输入的多项式函数g(v(t)),为表征非对称磁滞现象提供了基础。多项式函数的选取不是唯一的,后文中采用了输入的三次多项式函数。改进PI模型可以表征非对称磁滞现象,考虑到压电材料磁滞现象的非对称性,改进PI模型可以更好地描述压电的磁滞特性。 压电执行器的机械结构部分可以简化为质量-弹簧-阻尼模型,如图3所示。根据压电磁滞特性和机械结构的动力学特性可以建立如下方程 (8) 式中:H为压电的磁滞特性模型;Fe为压电产生的致动力;me为压电执行器的有效负载质量;x为产生的位移量;ce和ke分别为机械系统的等效阻尼和刚度。 图3 机械系统模型 机械系统的传递函数可以表示为 (9) 式中:ξ为等效阻尼比;ω为机械系统的共振频率。 上述三部分共同构成了压电执行器系统模型,系统的电路特性、磁滞特性和机械特性分别由式(1)、式(7)和式(9)描述。 根据压电执行器系统的模型结构,电路和机械模型的未知参数都有其物理意义,存在理论值,但是,考虑到实际系统的差异,为了准确描述系统特性,这些参数需要根据实验数据辨识得到,而且压电的磁滞模型参数也需要通过辨识获得。 系统磁滞特性和动态特性的耦合给系统参数的辨识带来了一定困难,可以采用分步辨识的方法部分解决耦合问题。对于动态特性部分采用小幅值方波信号作为辨识信号,利用预测误差最小化方法进行参数辨识;对于磁滞非线性部分采用变幅值正弦信号作为辨识信号,利用非线性最小二乘法进行参数辨识。整个辨识过程分为三步进行。 首先对电路的动态特性进行辨识,电路部分的输入和输出都是可测项,通过施加方波小信号,在带有实际压电负载的情况下,测量电路输入和输出电压,即可辨识得到电路参数。第二步需要辨识机械结构的动态特性,同样使用方波小信号作为激励信号,直接测量压电两端电压和输出位移量,进而可以辨识出机械系统参数。最后需要辨识压电材料的磁滞特性参数,由于磁滞特性部分的输出量不可测,因此,磁滞特性的辨识需要建立在电路和机械特性已知的基础上,基于辨识得出的线性模型,采用非线性最小二乘法进行辨识,优化的目标函数为 (10) 满足 (11) 电路和机械系统的增益都归一化为1,使整个系统的增益统一到磁滞模型中。 验证实验平台包括了压电执行器、功率放大器、应变片式微位移传感器和NI PXIe平台,实验布置如图 4所示。 图4 实验平台示意图 压电执行器采用预紧的压电平台(P841.1),其内部集成了应变片式微位移传感器,可以用来测量输出位移。功率放大器[11]可以将输入电压放大到0~100 V,信号调理电路将应变片的电阻变化量转换为输出电压变化,通过NI PXIe平台的16位模数转换器采集该电压。 为了验证非对称磁滞动态模型,需要首先辨识模型参数,利用第三节所述辨识步骤和方法对系统参数进行辨识,其中基础算子的个数M=10,算子的阈值ri取输入区间的均匀分布值,电路参数τ=5.4×10-5,机械系统参数ξ=1.31,ω=26 846,表 1为辨识得到的磁滞模型参数。 表1 非对称磁滞模型辨识参数 利用辨识得到的磁滞动态模型,首先在输入是简单缓变信号的条件下,对建立的非对称磁滞动态模型进行验证。 缓变输入信号下模型预测结果和实验数据的比较如图5所示,描述了压电执行器的滞回曲线,预测结果和实验数据的最大误差约为1.6%(最大误差和最大位移量的百分比),误差均方根约为0.065 μm,验证了改进PI模型对压电材料磁滞非对称特性的描述效果。 图5 缓变输入下模型实验验证 采用复杂多频组合信号作为输入信号进行实验,从而更加全面地验证非对称磁滞动态模型的正确性。同时为了证明非对称磁滞动态模型的优势,对比了线性模型、纯动态模型、纯磁滞模型和磁滞动态模型的预测误差。 v(t)=32-8×[cos(10πt)+cos(20πt)+ (12) 当输入信号为式(12)时,模型预测结果和实验数据如图 6所示,可以看出在频率较高时磁滞动态模型依然可以较好地描述压电执行器的特性。 图6 复杂输入信号下模型验证结果 磁滞模型和压电执行器系统的吻合度可以表示为 (13) 该数值越高,则表明模型越准确。表 2列出了低频和高频输入信号时,不同模型的吻合度和最大误差。从表中可以看出磁滞模型和磁滞动态模型的吻合度远高于线性模型和动态模型,在低频时磁滞动态模型和磁滞模型的吻合度基本相同,而高频时磁滞动态模型的吻合度更好。 表2 不同模型吻合度和最大误差 % 为了在更宽的频带上准确描述压电执行器特性,提出了基于改进PI模型的非对称磁滞动态模型。对于构建的磁滞动态模型,首先辨识系统的线性部分,包括电路特性和机械特性,然后在已知线性系统的基础上,辨识非对称磁滞模型,构建出系统的磁滞动态模型,最后对模型进行了实验验证,在缓变输入时,模型预测均方根误差为0.065 μm,最大误差为0.2 μm,高频输入实验也表明磁滞动态模型能更好描述系统特性,为基于模型的控制器设计建立了基础。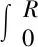
Fmr[v](t)=fmr(v(t),Fr[v](ti))
1.3 执行器动态模型

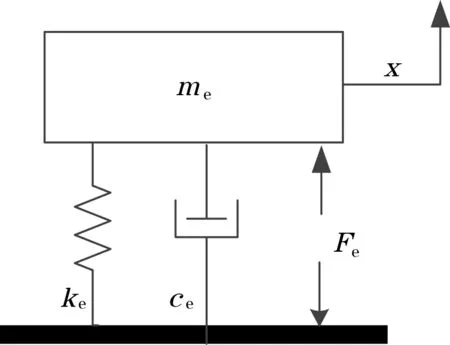
2 压电执行器系统辨识


3 实验验证


cos(60πt)+cos(100πt)]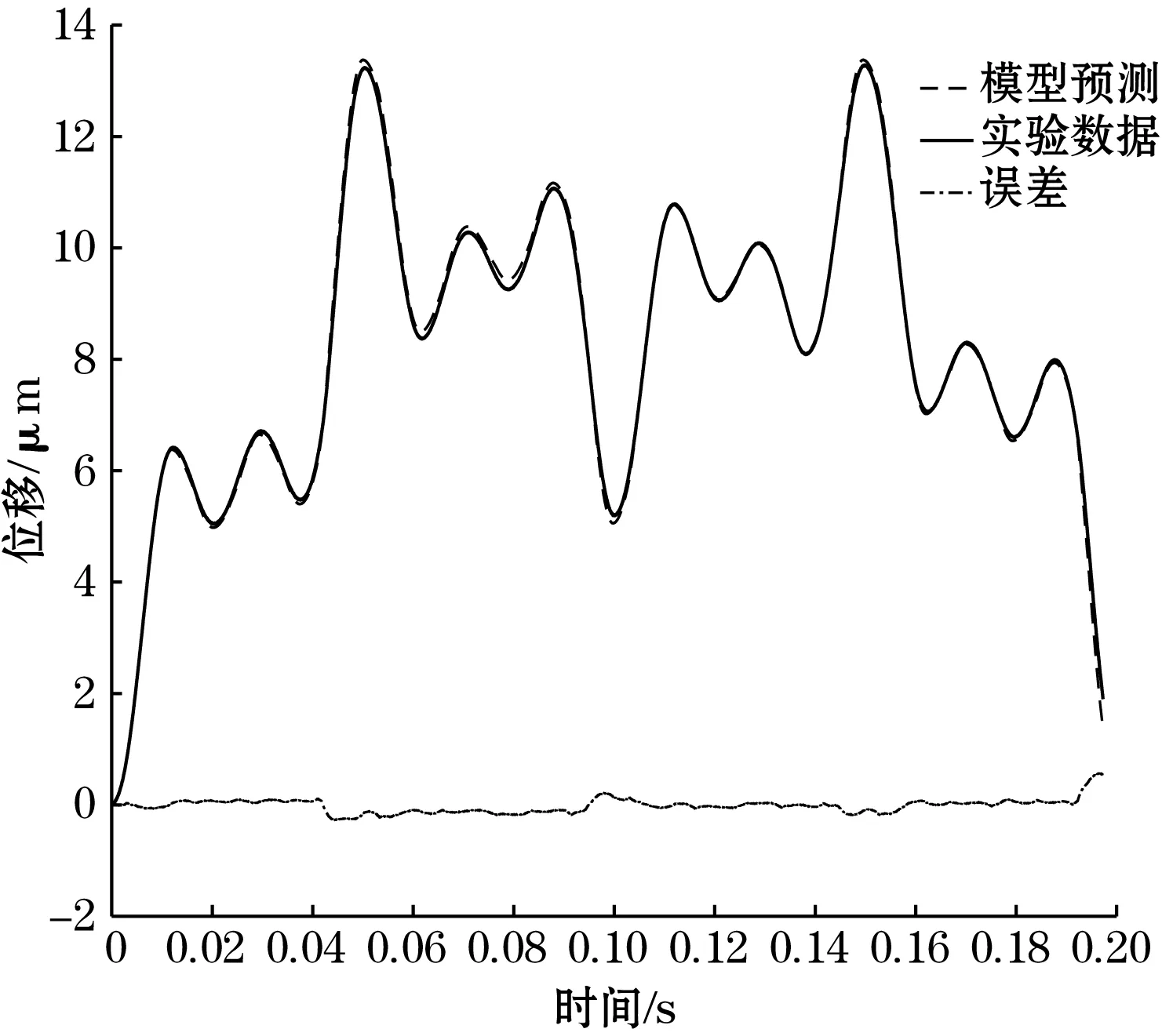


4 结论

