基于SURF算法和SLSH算法的图像定位方法
周 强,周 虎,徐利军,刘 涛,游 政,罗宾鸿
(1.东华大学机械工程学院,上海 201620;2.上海航天动力技术研究所,上海 201108)
0 引言
图像定位算法一般分为基于灰度信息和基于特征信息的算法。基于灰度信息的算法运算量小但不稳定[1];基于特征信息的算法则鲁棒性更强,效果更好,定位结果主要由特征提取和特征匹配两部分决定[2]。
特征匹配算法中SIFT算法具有较强的鲁棒性,能够保持很好的匹配稳定性。但是该算法生成的特征点数量多,消耗的匹配时间较长,且误匹配较多[3]。针对上述问题,Bay等人[4]提出改进后的SURF算法,该算法利用积分图像进行计算,由Hessian检测子来获取特征点。通过计算每个特征点的Harr小波变换确定特征点的主方向,进而确定特征点描述符,再根据特征描述向量之间的欧氏距离完成匹配[5]。SURF在理念上与SIFT类似,注重图像在不同尺度空间上的梯度信息,并在特征检测和描述向量的生成中充分利用积分图像和方框滤波器,减少了描述向量的维数,提高了特征匹配的速度[6]。但是当图像存在较大视角和噪声变化时,SURF算法提取的特征点比较不稳定[7]。因此,国内外一些学者基于SURF算法提出了一些改进:廉蔺[8]等人针对SURF算法中Harr描述符未能充分利用特征点的周围信息,提出加窗灰度直方图算法,实现特征点外围区域灰度差信息的利用;罗楠[9]等人通过在SURF描述符上增加领域采样点经过局部归一化后的灰度统计信息和二阶梯度值细节信息,得到扩展SURF描述符,同样实现特征点外围区域灰度差信息的利用;翟优[10]等人分析了在不同局部领域划分情况下SURF的性能,他们将SURF描述符的局部领域由原来的栅格状更改为三角形和扇形进行研究,发现分别采用栅格、三角形和扇形对SURF描述符的局部领域进行划分时,SURF算法的性能依次改善。
为了增加图像定位识别的效率,本文提出在使用SURF算法之前先通过双树复小波变换对图像进行分解,将图像分为高频和低频两部分,只将其中的低频部分作为SURF算法的输入图像得到特征描述子,再由SLSH算法实现特征降维得到最终的特征描述子;然后通过欧氏距离和最近邻次近邻比值法剔除部分错误匹配点对,完成粗匹配,再利用RANSAC算法构造仿射变换模型进一步剔除错误匹配点对,实现精确匹配,从而实现图像的精确定位。利用汽车线束上的接插件进行定位实验,给出实验结果,并与SURF算法、SIFT算法进行比较分析。
1 结合双树复小波变换和SURF算法生成特征描述子
1.1 双树复小波变换分解图像
为了提高SURF算法的运算速度和匹配精度,分别将目标图像与基准图像通过双树复小波变换分解成低频和高频两部分。其中,低频部分保留了原始图像的大部分信息,高频部分则携带有许多噪声。因此选择图像分解后的低频部分作为SURF的输入图像不仅能够减少运算量,还能提高图像配准精度[11]。双树复小波φ(t)用公式表示为
φ(t)=φh(t)+jφg(t)
(1)
式中φh、φg(t)为实数小波。
如图1所示,双树复小波包含树A和树B两个平行分解树,分别由两对不同的共轭正交滤波器构成,即h0(n)、h1(n)和g0(n)、g1(n)。输入信号A(j,1)经过双树复小波变换后将得到低频部分和高频部分,其中低频部分由A(j+1,1)和A(j+1,2)组成,依次代表了实部和虚部;高频部分则由6个高频子带D(j+1,n),n=1,2,…,6组成。
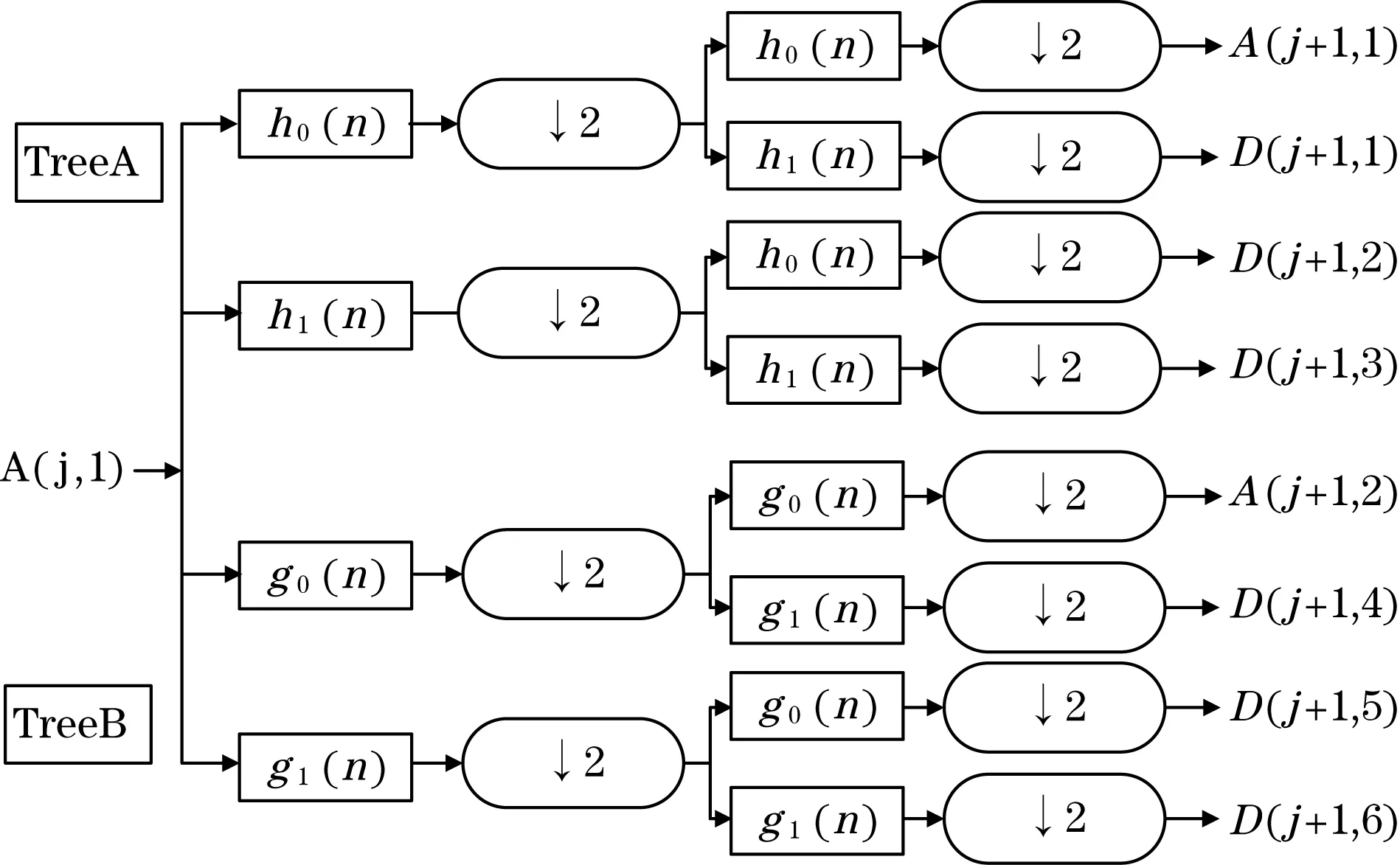
图1 双树复小波变换的分解结构图
1.2 特征点检测
特征点是图像精确配准的关键[11],SURF算法利用积分图像和方框滤波器来加快运算速度[6],并采用快速Hessian矩阵算法对特征点进行检测。积分图像的设定为[12]:设I=(x,y)表示图像I(x)的某一个像素,则点(x,y)的积分值可表示灰度区域,如图2所示。对I(x)进行积分,得到I(x)左上角到任意点(x,y)的灰度值总和,即
(2)

图2 积分图像
选取图像I(x)中的任意一点X=(x,y),该点在σ尺度上的Hessian矩阵定义为
(3)

(4)
实际应用是通过箱式滤波器代替二阶高斯滤波来提高速度。基本原理[3]为:使用箱式滤波器模板与输入图像的卷积Dxx、Dxy和Dyy来代替式(3)中的Lxx(X,σ)、Lxy(X,σ)、Lyy(X,σ),用9×9的箱式滤波器代替尺度σ=1.2的二阶高斯导数,Dxx、Dxy和Lxx、Lxy的关系为
(5)
式中:‖·‖F为Frobenius范数;ω为权重系数,取其近似值0.9。
则Hessian矩阵的行列式可近似表示为
det=DxxDyy-(0.9Dxy)2
(6)
点(x,y)经过式(6)的计算可得出该点的角点响应值。同理,对图像上所有的点进行计算将得到同一尺度下的角点响应图像。采用不同尺寸的模板进行计算,便可构造出图像金字塔。将所有角点响应值小于预设值的像素点舍弃之后,再将剩余的每个像素点与其同尺度点及其上下相邻尺度共26个像素点进行比较,通过非极大值抑制(non-maximum suppression,NMS)和插值运算得到特征点[13]。
1.3 特征描述子生成
首先确定特征点的主方向:以特征点为中心,在半径为6σ(σ为特征点所在尺度空间的尺度值)的圆形领域内,计算各点在x和y方向的Harr小波响应,并用特征点为中心的高斯函数对响应值进行加权计算;按每次5°的步长转动张角为60°的扇形窗口,累加不同窗口内的Harr小波响应值,将其作为局部方向矢量,其中矢量最长的方向为主方向。
然后构建描述子:将平面坐标系的y轴旋转到主方向上,以20σ为边长选取一正方形区域,并以特征点作为该正方形区域的中心。再将正方形区域根据特征点的主方向进行均等划分,分成4×4个大小相同的小正方形,再分别将这16个小正方形区域分成5×5个大小相同的子区域。计算每个子区域内所有像素点沿x和y方向的Harr小波响应值并高斯加权,得到∑dx和∑dy。为了表征图像灰度值变化的极性信息[1],同时计算∑|dx|和∑|dy|,由此生成4维描述向量:v=(∑dx,∑dy,∑|dx|,∑|dy|)。将所有子区域的描述向量串联便得到64维的特征向量,但由于特征维数太高增加了计算量,很难快速实现基于特征的图像相似度分析,需要通过降维的方法来简化特征和提高处理速度,采用类局部敏感哈希降维法(SLSH)实现这一目的[14]。
先随机生成L个投影矩阵W1,…,Wi,…,WL,每个投影矩阵都是D×K维,其中D是特征向量维度;K是单个矩阵投影之后的数据维数;再将高维特征X分别在L个投影矩阵上投影,并将投影之后的数据特征进行前后连接,形成低维数据特征H,从而得到最终的特征描述子[11],如式(7)所示
H(X)=[XW1,…,XWi,…,XWL]
(7)
式中投影矩阵Wi通过式(8)生成
(8)
式中:RDK(-1,1)是一个[-1,1]区间的D×K维的随机矩阵;c为固定参数。
2 结合RANSAC算法进行图像定位
利用提取的特征向量和特征点即可实现图像配准定位,但由于一些错误匹配特征点的存在,会降低匹配精度,原始SURF算法利用欧氏距离和最近邻次近邻比值法能够有效剔除部分错误匹配点对,但不能保证完全剔除,因此结合RANSAC算法能够进一步将错误匹配点对剔除,提高匹配精度[11]。
2.1 RANSAC
RANSAC 算法的主要思想[1]是:构造一个仿射数学模型,通过不断随机抽取样本中的点对,以求取该数学模型的仿射系数,根据仿射系数把经过粗配准后留下的点对分为内点和外点。其中,内点是满足仿射变换关系的配准点对,外点则是不满足该变换关系的配准点对。然后选择拥有最多内点的点集,通过最小二乘法利用这些内点重新计算仿射数学模型的系数,实现图像的精确配准。具体方法如下:
先假设两副图像满足仿射变换关系[11]
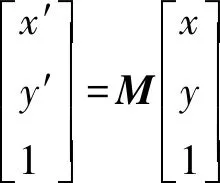
(9)
式中M为变换矩阵,
式中:a1、a2、a3、a4、a5、a6为仿射系数;(x,y)和(x′,y′)分别为基准图像和目标图像的特征点坐标。
然后进行以下操作:
操作1:随机从所有匹配点对中取出3组,通过计算得出变换矩阵M中6个仿射系数的值;
操作2:将计算出的6个仿射系数带入变换矩阵,并利用生成的变换矩阵对目标图像中的所有特征点进行变换;
操作3:计算出经过变换后的特征点与参考图像中的对应特征点之间的距离d,并将该距离与设定的距离阈值进行比较,若距离大于阈值则设为外点,反之则为内点;
操作4:多次随机选出不同的3组匹配点对,并重复操作1至操作3的步骤,然后从得到的所有内点集当中,选出点数最多的点集作为目标点集;
操作5:将目标点集内的点,通过最小二乘法重新计算仿射模型变换矩阵M的系数。
操作6:根据仿射变换模型实现图像的精确配准和定位。
2.2 基于改进SURF的精确定位算法流程
综上所述,基于改进SURF的精确定位算法流程可表述为如图3所示。
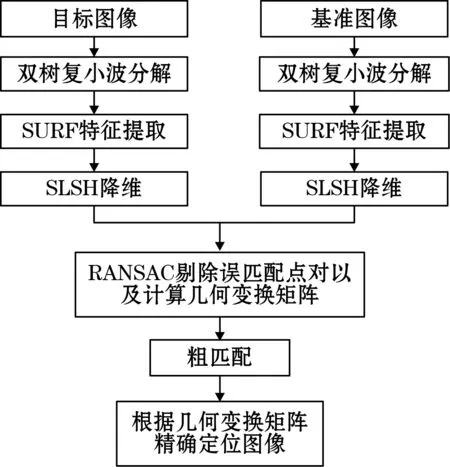
图3 基于改进SURF的图像精确定位算法流程图
3 实验及分析
利用汽车线束上接插件对本文提出的基于改进SURF算法的图像精确定位方法进行有效性验证,并通过实验将本文提出的方法与SIFT算法、SURF算法进行比较。实验的硬件环境是64位Windows 7系统,CPU为Intel core i3,2.40 GHz,内存为4 GB;软件开发平台是OpenCV 3.0和VS2013。
采用本文方法的实验过程如下:
首先利用双树复小波变换对输入的图像进行分解,需要分解的图像包括基准图像和目标图像,接着分别将分解后的图像低频部分输入SURF算法中生成各自的特征向量,再由SLSH算法实现降维;然后部分错误匹配的点对将先通过欧式距离和最近邻次近邻比值法进行删减,完成粗匹配;再将剩余的大部分错误匹配点对通过RANSAC算法进一步剔除,完成精确匹配,进而实现图像的精确定位。
图4是汽车线束的全景图,将其作为基准图像。图5是汽车线束上4个不同的接插件,将其作为目标图像。这4个接插件在基准图像上的对应位置由虚线圆指示,并分别标有a,b,c,d,如图4所示,实验需要达到的效果是依次输入接插件的4张目标图像之后,能通过本文方法在基准图像上找到该目标在基准图像上的对应位置。
图6是采用本文方法进行实验的结果图,表1为相应的实验数据。

图4 汽车线束全景图

(a)

(b)

(c)

(d)

(a)

(b)

(c)

(d)图6 实验的结果
从表1中可以发现,采用本文提出的方法对不同目标图像进行定位,其定位正确率一般都能维持在80%以上,而且所消耗的时间都在1 s之内,可见本文方法具有一定的时效性。
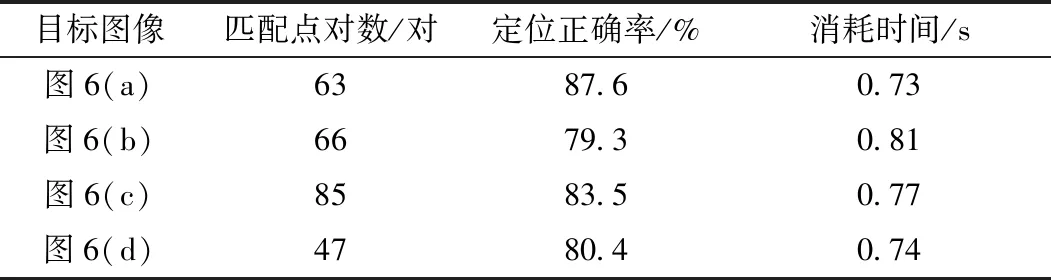
表1 采用本文方法的定位结果
为进一步验证算法的性能,将本文方法与SURF和SIFT进行了比较,比较结果如表2所示。
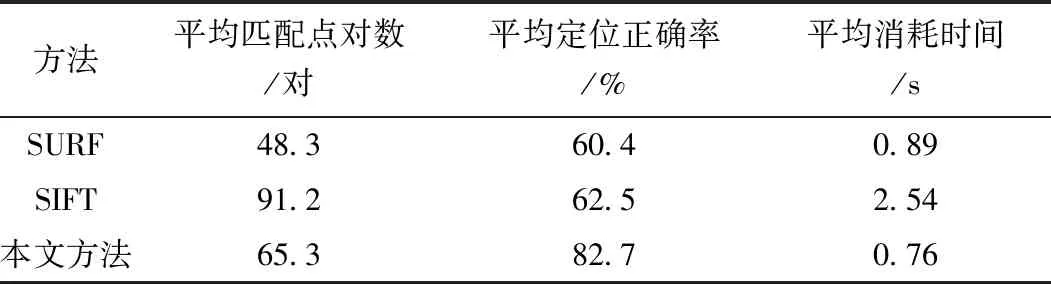
表2 本文方法与SURF、SIFT算法性能比较
从表2可以发现,SIFT算法得到的平均匹配对数最多,为91.2对,比SURF算法得到的匹配点数多了将近一半,也比本文方法多了将近三分之一。但SIFT算法消耗的时间也远多于其他两种方法,是SURF算法的3倍左右。本文方法则是3种方法中耗时最少的,而且定位的正确率也是最高的,平均定位正确率可以达到82.7%,比SIFT算法和SURF算法都要高出20%以上,可见本文方法与SIFT算法和SURF算法相比具有较大的性能提升。
4 结论
本文提出了一种基于改进SURF算法的图像精确定位方法。首先将目标图像与基准图像利用双树复小波变换分解为高频和低频两部分,再将其中的低频部分作为SURF算法的输入,得到特征向量后由SLSH算法进行降维;特征匹配时,先进行粗匹配剔除部分错误匹配点对,再通过RANSAC算法剔除其余错误匹配点对得到拥有最多内点的点集,并利用这些点集内的点求出仿射变换模型的系数,实现图像的精确定位。利用汽车线束上的接插件进行算法有效性验证实验,实验结果表明,本文算法相比SIFT算法和SURF算法拥有更高的定位精度和更快的运算速度。

