仿射跳扩散模型下权益指数年金定价

安顺学院 赵彩霞

权益指数年金（EIA）与市场股价指数相关，是一种利率变动型年金产品，股价指数也可能会有剧烈波动，不再遵循几何布朗运动。（Duffie（2000））等人指出将跳跃风险也加入基础资产的波动率模型中，提出了随机波动率跳扩散模型。本文主要研究仿射跳扩散模型下点对点法EIA的定价。

一、预备知识

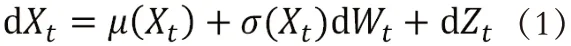
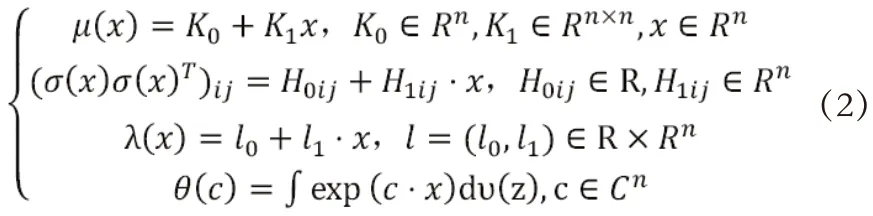
为了与Vasicek 利率模型保持一致，具有均值回复平方根过程特点。可以令，则利率模型为:

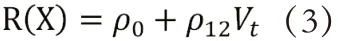
引理 若股价指数满足式（1）－（3），定义联合特征函数：

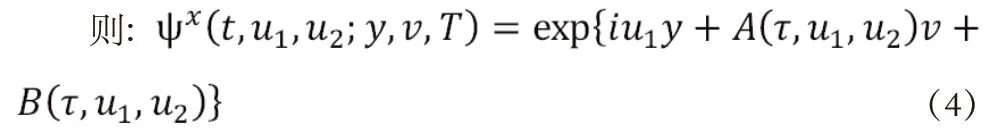
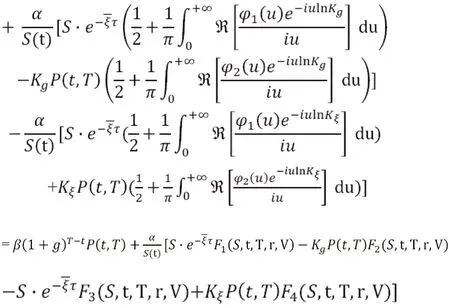
由引理的特征函数

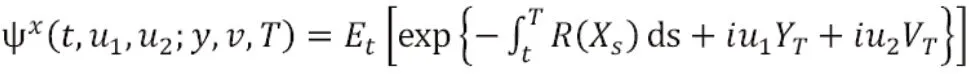
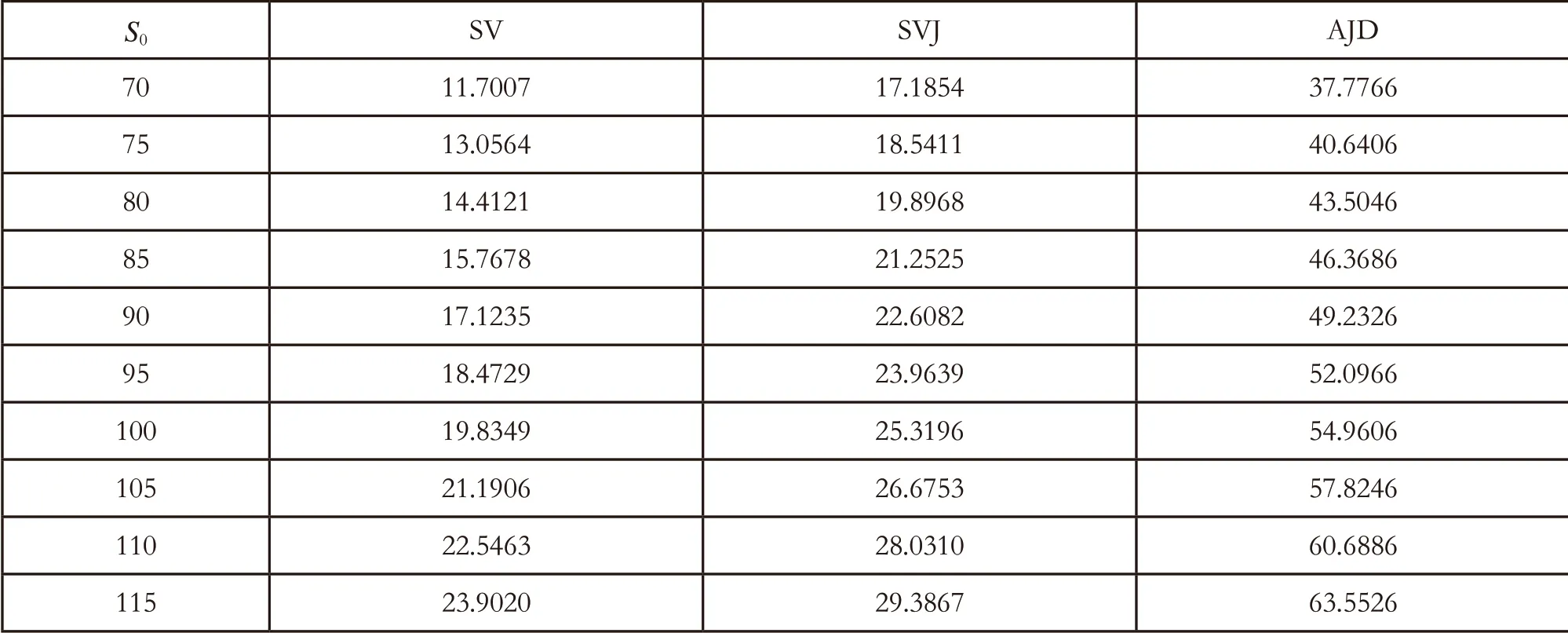
表1 不同模型下EIA 价格的比较

可得：

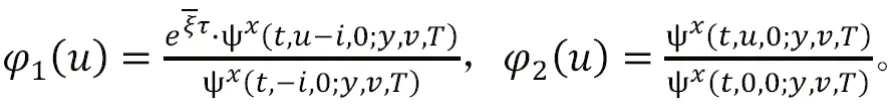
二、结果分析

比较经典模型与在仿射跳扩散模型下权益指数年金产品的价格的变化。从表1 可以看出，二维双跳仿射跳扩散模型对权益指数年金的价格的影响要比随机波动率模型以及跳跃扩散模型下其价格影响要大得多。首先跳跃风险存在于基础资产对权益指数年金价格有影响，并且股价与其波动率的共同跳跃比基础资产单独跳跃对权益指数年金的价格的影响要大很多。所以，市场中的跳跃风险对股价及其波动率的共同跳跃是我们以后研究的重点，对权益指数年金价格的影响比较大。

三、结论

本文应用随机波动率及跳跃均存在于股价指数和波动率的仿射跳扩散模型，假设市场利率依赖于市场随机波动率，对权益指数年金定价研究。应用二维特征函数和Fourier 变换法，给出了在简单点对点法下权益指数年金的期权定价公式。最后，运用matlab 软件编程比较了经典模型与本论文模型权益指数年金产品的价格的变化。本文对权益指数年金的定价研究将对我国保险市场的发展产生影响，同时对我国解决人口老龄化问题也有借鉴作用。