基于模态试验验证的赛车车架优化设计

（江西理工大学 机电工程学院，赣州 341000）

0 引言

方程式赛车车架的优化有助于实现整车动态特性的改善。针对车赛车车架动态特性的基础研究有以下几个方面：马芳武等[1]对FSC车架进行了轻量化，在满足频率、强度、刚度约束的前提下，对多种工况进行车架性能分析，以质量最小为优化目标，通过序列线性规划对非线性模型进行求解，达到尺寸优化质量减小的结果；李芳等[2]通过Hyperwork中的Optistruct模块在多种工况下对车架进行拓扑优化，并对优化后的车架进行对比分析，验证了设计的合理性；兰凤崇等[3]结合整车多工况多体动力学分析，对赛车车身结构进行综合目标拓扑优化，以设计经验和正交实验定义权重系数得出优化结果，提高了结构的动态特性，达到优化的要求；余海燕[4]等采用碳纤维复合材料铝蜂窝板为材料，对车身进行了单体壳设计，进行尺寸优化和铺层优化，对剪切强度和弯曲刚度进行校核；其中，利用有限元方法对车架进行动态特性分析和优化设计成为重要方式，刊出了大量的理论研究和应用成果。但是这些研究缺乏试验验证，特别是有限元模型的准确性无法保证。

通过结合计算模态和试验模态的方法，对赛车车架进行结构优化设计，利用模态验证证明有限元模型的准确性，通过Topology Optimization模块，以质量最小为优化目标对车架壳体进行拓扑优化分析，开展车架结构的优化设计。

1 车架的计算模态和试验模态分析

1.1 车架有限元建模分析

为提高有限元建模精度，有限元模型具有UG建立的三维模型相同的尺寸，对车架上的固定吊耳和钢管的焊接口进行简化处理。采用ANSYS Workbench中的Modal模块，开展几何模型的前处理和网格划分。经过简化后的三维模型以X_T格式导入ANSYS中，并选择材料为30CrMn的钢管，其弹性模量为E=2.11×1011Pa，泊松比为μ=0.279，密度为ρ=7850Kg/m3。为了提高计算精度，减少计算量，采用20mm的单元进行网格划分，图3所示，单元总数246568个，节点总数99237个。

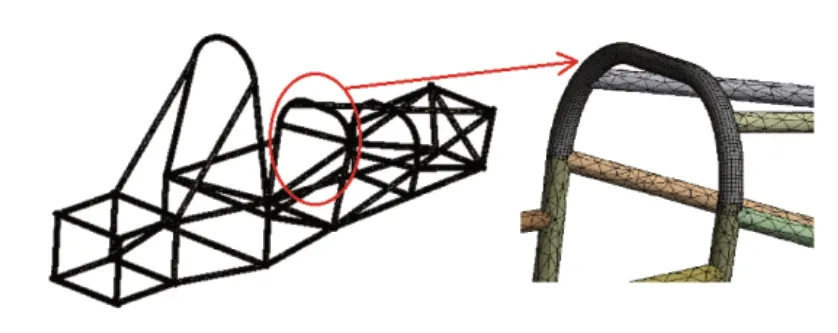
图1 车架有限元模型图

1.2 车架自由模态分析

在ANSYS的Modal求解器中进行车架的自由模态分析，采用自由边界条件，不施加任何约束和载荷。通过子空间法（Subspace）进行模态提取，该方法运用广义Jocobi迭代算法，对完整的刚度矩阵和质量矩阵进行分析，运算精度高[5]。提取得出车架的前12阶模态，由于前6阶固有频率较小，振型情况分别为三个轴向平动和绕三个轴转动，可判断前6阶属于刚体模态，所以应剔除前6阶计算模态，第7阶实际为车架的第一阶模态，得出车架前6阶真实的模态和振型如表1所示，第1阶和第2阶图2所示。

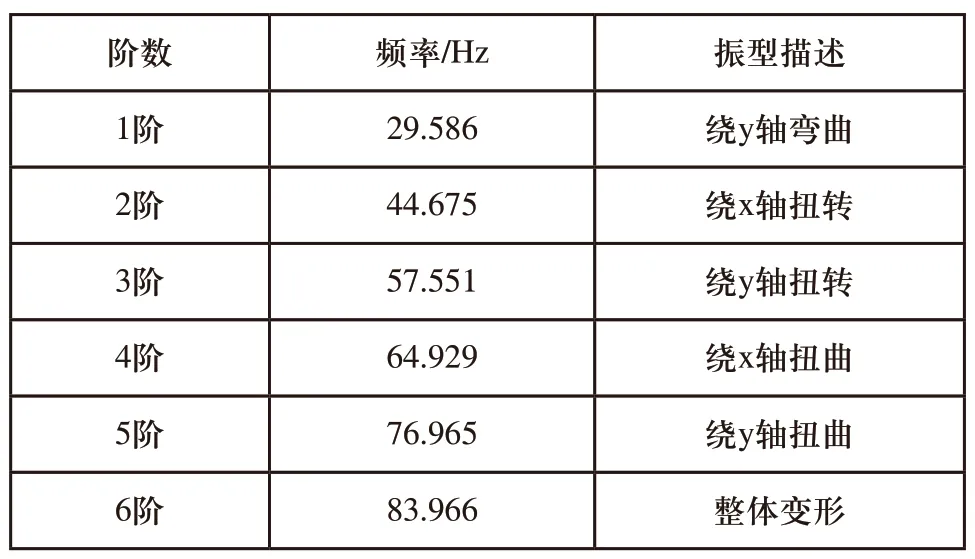
表1 前6阶模态和振型情况

图2 第1阶和第2阶振型图

2 车架的试验模态分析

2.1 试验测试系统分析

利用DHDAS模态测试系统，对车架进行试验模态分析如图3所示。考虑到现实条件无法让车架悬浮在空中，为保证计算模态和试验模态的自由边界条件一致，试验模态分析中可采用支撑或悬挂的方式进行模拟自由边界。本实验采用柔软的橡皮绳进行悬挂，满足支撑或悬挂的刚体频率小于被测结构的最低弹性模态的10%～20%，实现了自由边界的模拟[6]。

图3 模态试验现场和流程图

不同的结构对激励方式的选择不一样，一般激励方式有激振器激励和锤击激励，激振器激励优点有多种激励信号可供选，测试速度快，激励能量大。缺点位置固定安装，操作复杂有附加质量影响。锤击激励的优点设备简单、投资少、移动方便且适用于线性结构，缺点是信号采集容易过载或欠载[7]。车架属于钢架焊接结构，线性动态特性好，因此采用锤击激励。合理选取测试点的位置便于测量容易识别，再参考计算模态振型，对变形大的地方可多布置测试点。以下对车架进行了34个激振点和1个响应点，通过拓扑图对车架进行建模，如图4所示。

图4 拓扑图与测试点的分布

首先对车架进行预实验测试分析，找出合适的响应点和激励方向，能够使得最远端激励采集到高质量的响应信号，通过预实验分析能够节约实验时间，提高实验效率。在实验中，采用单输入单输出法（SISO）进行信号分析，选择20点为响应点，测试Z方向的模态，布置加速度传感器于竖直方向，传感器本身的重量相对于车架可忽略不计。每次锤击在同一个点（很小区域）并保持Z轴竖直方向激励，并多次锤击同一激励点，有利于消除结构动态非线性的影响和提高信噪比。在激励每个点的时候，要识别出相应的传递函数，并且检查该点的激励信号和响应信号的相关性，使得0～95Hz频率的相关系数在0.8以上[8]。图5所示为测试点13的相关性系数。

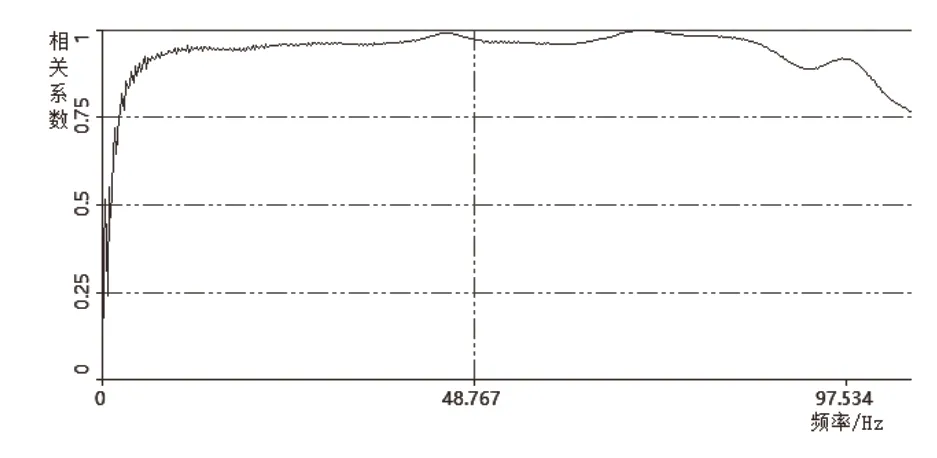
图5 激励信号和响应信号的相干函数图

经过多次测试，在DH5922N软件采集了34个点的信号，并通过PolyLSCF模态识别法对数据进行频域拟合分析，在SUM函数识别下，得到各阶模态参数，根据最小二乘频域法估计振型。

2.2 试验结果的验证分析

模态置信准则（MAC）是用来检验模态试验得出得模态参数是否准确的一种评判准则，也称为振型符合度，下列是模态置信准则（MAC）计算公式：

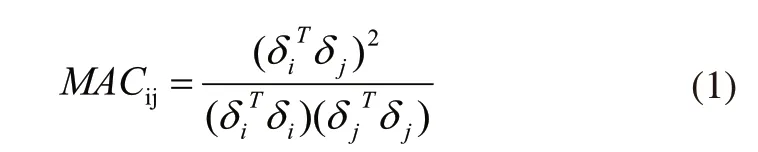
图6 模态置信准则（MAC）图

从图中可知，该试验得到的对角线的振型向量MAC值都为1，非对角的振型向量MAC值最大仅为0.26，在误差应许范围内，证明各振型向量相互独立互不影响，试验求得得模态参数比较可靠[10]，为计算模态的对比分析提供了有力的根据。

2.3 计算模态和试验模态相关性分析

计算模态结果与试验模态的结果进行固有频率相关性分析，相关性分析的公式为：

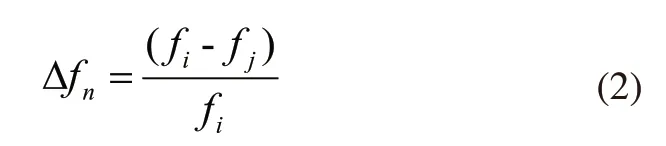
fi表示计算固有频率，fj表示试验固有频率，表示相对误差。由于试验受到环境、设备等因素的影响会产生相对误差，如表2所示最大仅为6.375%，其他的在5%以内，可见的都在5%左右，在误差的可接受范围，证明建立的计算模态具有准确性，为后面的优化奠定了基础。

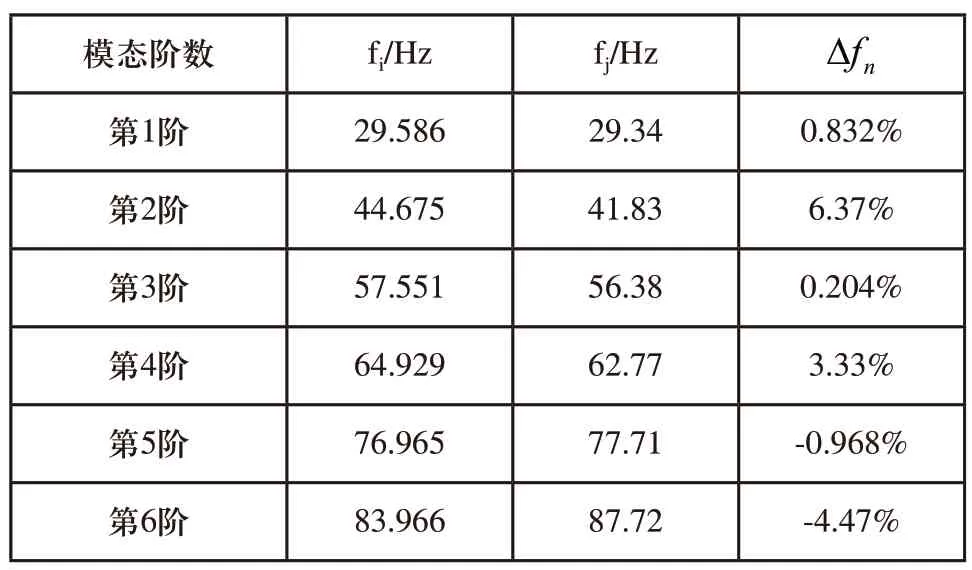
表2 计算固有频率和试验固有频率的相关性分析

3 结构设计改进

3.1 拓扑优化分析

为提高结构的动态特性，对车架的杆件空间进行设计。首先在原车架的基础上通过UG对外形进行壳体建模，利用ANSYS WORKBENCH的Topology Optimization模块，开展壳体模型的前处理和网格划分。材料属性为弹性模量E=2.11×1011Pa，泊松比μ=0.279，密度ρ=7850Kg/m3。为达到优化效果，壳体单元的厚度和管道外径相等。再定义网格单元为20mm，对壳体进行网格划分，建立了拓扑优化有限元模型[11]。车架吊耳的分布图中只标出了一侧，如图7所示。

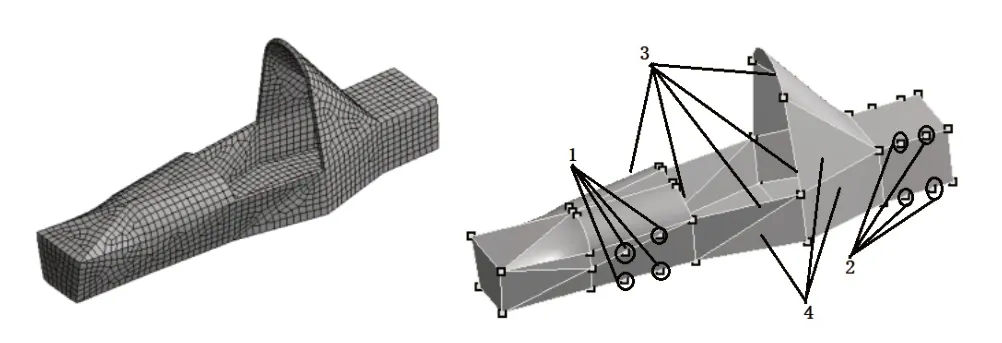
图7 车架壳体有限元模型

首先对车架的全部杆件轮廓线选定为非设计区图7所示，对剩下的区域进行壳体填充进行拓扑优化。然后对模型确定载荷和边界条件，由于典型的四种工况分为弯曲工况、转弯工况、两种扭转工况，本文采用扭转工况下的对车架进行拓扑优化，在吊耳处施加扭转工况，对前车架的吊耳z方向设定为1mm其他为零，后车架的吊耳，对x，y，z方向设为零，释放其余的自由的[12]。

图8 单工况下不同约束条件下的优化图

以上对壳体单元的网格划分和工况加载已经完成，还有对约束条件的定义，在response Constraint处分别设定保留质量35%和45%，对 Objective面板中定义mincomp，经过19次的优化迭代，得出如图8的优化结构。

3.2 优化车架模态对比分析

根据以上拓扑优化的结果，对车架进行二次设计，得到新车架图9所示。基于对初始车架计算模态分析的准确性，再次以相同的参数设定对优化模型进行模态分析。

图9 优化前后的车架图

如表3所示，由于低价模态更容易被外界振动所激励，提高第一阶频率有效的提高了车架的动态性，在表中第1阶频率改善了11.8%，并且车架的变形量得到改善，如图5所示第5阶优化前和优化后振型，可见拓扑优化结果明显。

表3 初始车架与优化后固有频率比较

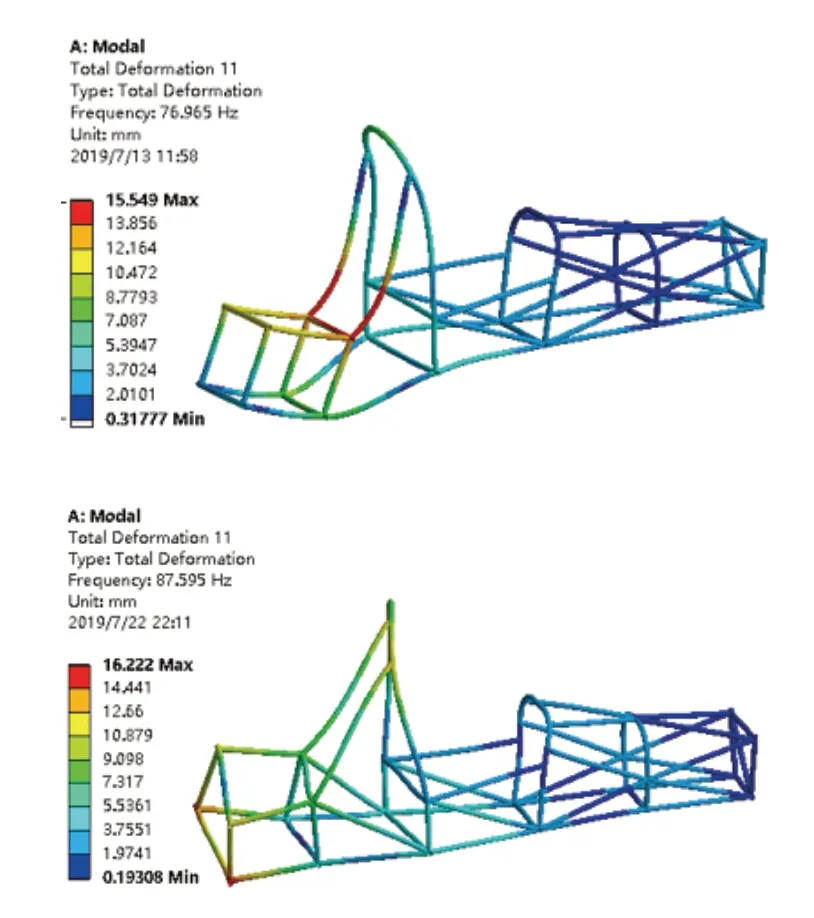
图10 第5阶优化前和优化后振型图

4 结语

通过UG三维软件建立赛车车架模型，在ANSYS Workbench的modal求解器中选取子空间法（Subspace）进行模态提取，得到车架前6阶的非刚体模态参数。

在MAC验证了试验模态准确性的基础上，通过计算模态和试验模态相关性分析，表明相对误差都在5%左右，该误差在合理的范围内，则计算模态和试验模态分析结果相吻合，验证了计算结果的准确性。

为提高赛车的性能，对赛车车架进行拓扑优化。结果表明：前6阶模态中都有很大的改善，第1阶提高了11.8%，第4、5、6阶都提高10%以上，降低车架的振型变形量，为赛车车架的设计提供了有价值的参考。