基于核极限学习机的快速主动学习方法及其软测量应用

代学志，熊伟丽

（江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122）

引 言

在复杂工业过程中，需要对一些决定产品质量的关键变量进行监测和控制，但由于现场环境以及技术条件的制约，使得这些变量难以在线测量。软测量[1-3]是工业过程中用于解决难测变量检测的常用技术，通过训练集构建数学模型，实现对新样本质量变量的实时估计。常见的软测量模型包括支持向量回归(support vector regression,SVR)[4]、人工神经网络(artificial neural network,ANN)[5]、高斯过程回归(Gaussian process regression,GPR)[6]和极限学习机(extreme learning machine,ELM)[7-8]等。

软测量技术通常需要大量标记数据才能完成模型训练，而在实际工业过程中常常是无标记样本数量多，有标记样本数量较少，而且获取成本高。在这种情况下，如何利用大量无标记数据和少量标记数据来提升模型性能成为软测量建模的关键问题。因此半监督学习[9]和主动学习[10]被提出并得到快速发展，并被广泛应用于图像检测[11]、故障诊断[12]、网络安全[13]和工业过程建模[14-15]等领域。

主动学习通过引入“人在回路”的环节提升模型性能，具体实施过程是利用样本选择策略挑选有价值的无标记样本进行标记，并将这些标记数据添加到训练集优化模型参数，当达到预设的终止条件时，迭代学习过程终止，从而实现以最小的标记代价实现模型性能的提升。在这种学习框架下，许多学者围绕样本选择策略[16-22]进行了大量研究。Norkus 等[20]将主动学习与高斯过程回归结合，通过减小方差有效解决了主动学习中的样本选择问题。Demir 等[21]提出一种支持向量回归的多准则主动学习方法，利用支持向量回归和核k 均值聚类进行信息评估，有效扩充了建模空间。Tang 等[22]通过分析核主成分分析和高斯过程回归的关系，引入不确定度和代表性指标对无标记样本进行信息评估。然而上述三种评估算法的训练时间较长，运行效率较低。

相比于支持向量回归等建模方法，ELM 的运算成本低，泛化能力强。Huang 等[23]将核函数引入ELM，提出核极限学习机(kernel extreme learning machine,KELM)算法，进一步提升了ELM的鲁棒性，并被广泛应用于软测量建模过程。杨锡运等[24]提出了一种基于粒子群优化的KELM 模型，并在风电功率区间预测中取得较好的效果。张雷等[25]将KELM与Gath-Geva 聚类算法相结合，有效解决了多阶段间歇过程的软测量建模问题。在主动学习方面，Qian 等[26]将KELM 引入主动学习，并根据softmax 模型构建无标记样本的评价机制，有效提升了信息评估的精度。然而上述方法在每次迭代过程中需要重新评估无标记样本信息，降低了迭代过程的运行效率，导致运算成本的增加。

综上所述，本文提出一种基于核极限学习机的快速主动学习方法，利用KELM 的预测输出与目标输出的误差进行无标记样本置信度的定义，同时考虑算法迭代过程的快速性，引入矩阵反演公式对样本选择策略进行优化，提升了迭代过程样本评估的运算效率；应用矩阵相似度理论对迭代过程的标记数据进行分析，并根据相似度指标度量已标记样本信息设计算法的终止条件。将所提方法应用于硫回收过程的SO2和H2S浓度的软测量，验证了所提方法的有效性和优越性。

1 核极限学习机

极限学习机是一种单隐层前馈神经网络模型[23]，可以通过KKT 理论计算网络输出权值。给定n 个训练样本{X ∈Rn×m,t ∈Rn}，m 为输入变量维数，ELM 的优化目标是最小化训练误差和输出权重的范数，ELM的优化函数可以表示为：

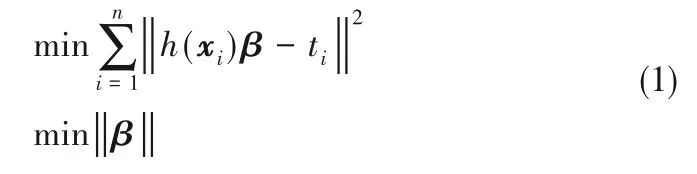
其中，β 是隐含层到输出层的输出权重向量，h(xi)为xi的隐层映射。

ELM的优化函数可以等价为：

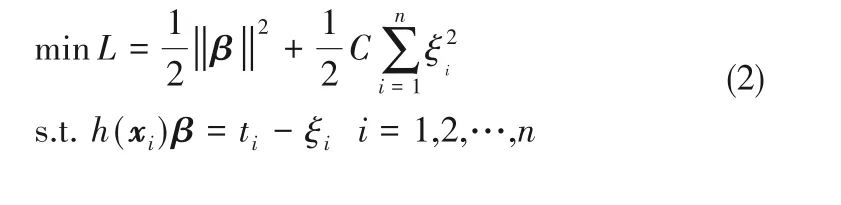
式中，ξi为训练误差，C 为惩罚系数，用来权衡模型的训练误差和输出权重。根据KKT 最优化条件解得：

其中，H 为隐层映射矩阵，T =[t1,…,tn]T为目标值矩阵，I为单位矩阵。

应用Mercer’s条件定义KELM的核矩阵为：

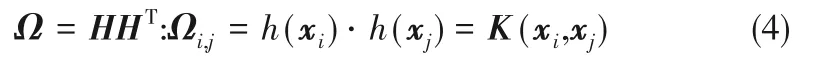
其中，K(xi,xj)为核矩阵Ω 的第i 行、第j 列的元素。

通常选择径向基核函数作为KELM 模型的核函数：

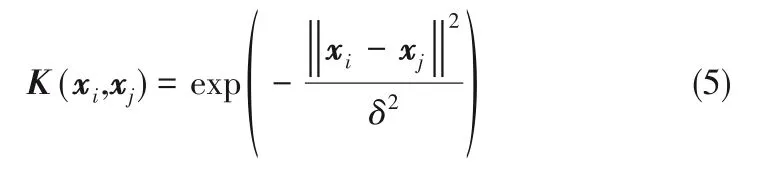
其中，δ为核函数参数。

则KELM的预测输出表达式为：

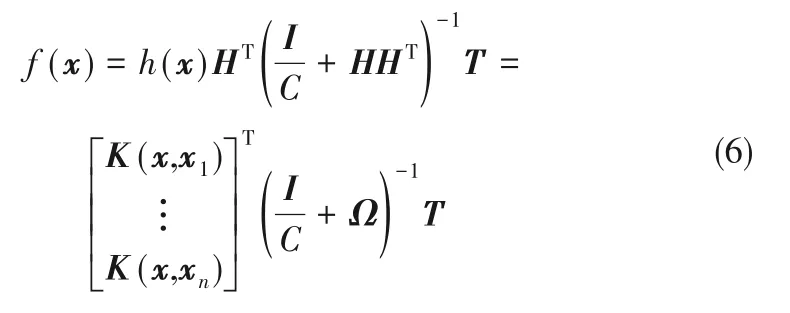
2 基于KELM的快速主动学习方法

所提的主动学习方法主要从样本选择、迭代更新和终止条件三个方面进行了改进。首先，为了更加准确地评估无标记样本，利用KELM 算法计算无标记样本的置信度，并以此作为样本选择依据。其次，充分考虑上一轮迭代信息，引入矩阵反演公式对评估算法进行优化，以加快主动学习的迭代更新过程。最后，为了使主动学习迭代过程及时终止，利用矩阵相似度理论对迭代过程的已标记样本数据进行信息度量，并将其作为终止依据，从而实现了以最小的标记代价获得模型性能的提升。

2.1 基于KELM的样本选择

主动学习主要是利用无标记样本信息改善模型性能，其核心思想是选取置信度较低的样本进行标记。所提主动学习方法是根据KELM 的预测输出与目标输出之间的误差来构建无标记样本的置信度指标，若样本的置信度较高，表明该样本对于已标记样本集是信息冗余的；反之则表明该样本包含了额外信息，若对该样本进行标记，则能有效扩充模型信息，提升KELM模型的预测性能。

其中，HL为标记样本的隐层核映射矩阵。将式(7)进行标准化，可以得到：

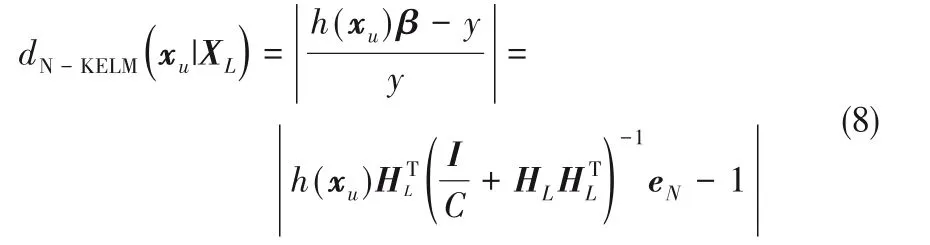
其 中，eN=[1,…,1]T∈Rnl。 根 据 误 差 指 标dN-KELM定义无标记样本的置信度：

其中，η ∈(0,1)，当η 趋近于1 时，说明该样本数据与现有的已标记样本集在本质上是相同的；反之，若η 趋于0 时，则说明对应的样本数据极有可能漂移出KELM 模型空间，标记该样本后能够为KELM模型提供更多额外信息。

2.2 快速迭代更新

主动学习过程中，每次标记新样本后都必须重新计算评估模型参数，随着迭代的进行，评估算法的运行效率将越来越低。为了进一步降低KELM 评估算法的运算成本，本文将样本评估过程分为初始化阶段和快速迭代学习阶段，根据给定训练集构建初始KELM 评估算法，同时保存本次评估过程的运算信息，在迭代学习阶段，充分利用已有的运算信息，减少不必要的迭代计算过程，同时引入矩阵反演公式对评估算法进行优化，以此提升评估算法的运行效率。

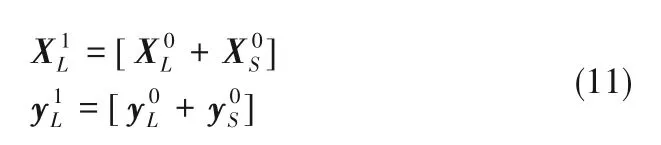
在无标记样本集中删除所选的样本：

Pk可以表示为：

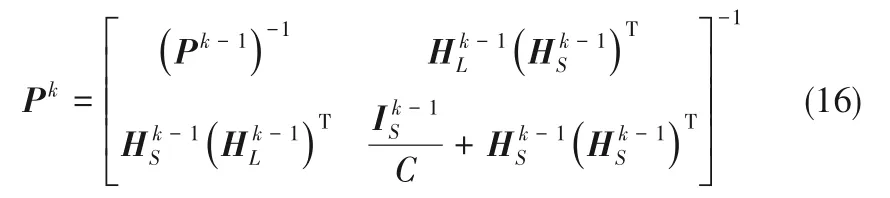
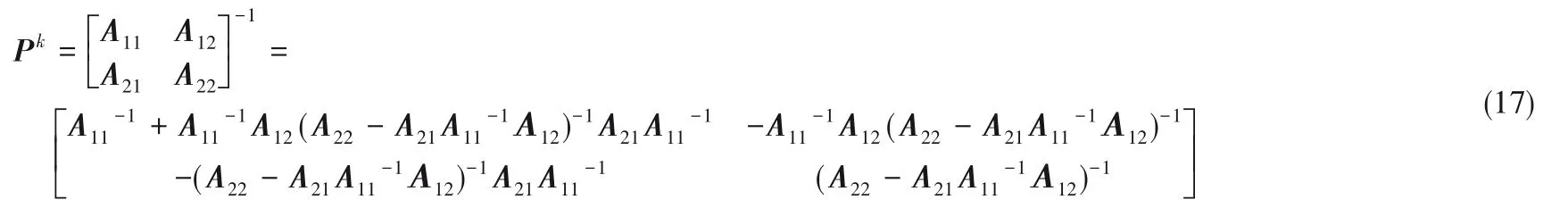
2.3 终止条件设计

主动学习的终止条件通常是标记代价达到一定指标，该指标根据实际情况预先设定，但无法表征标记样本集的信息量。本文为了使主动学习及时终止，进一步提升学习效率，引入矩阵相似度理论[28]对标记样本集建立信息评价机制，通过对迭代过程的标记数据进行分析，得到样本数据间的相似度，并根据相似度指标度量标记样本的信息量变化，其基本原理如下。

对Rmix进行特征值分解，得到一个正交矩阵P0：

则Yi的协方差矩阵Si为：

由式(22)可得：

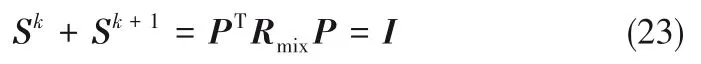
根据式(23)可以得到：

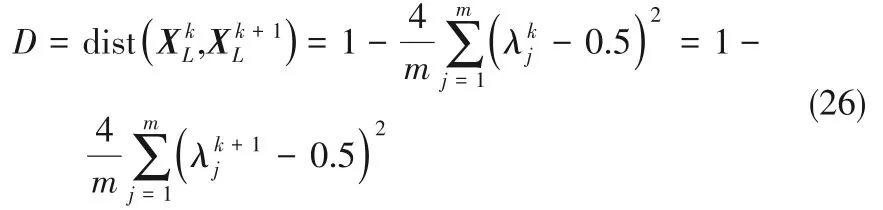
根据式(26)可知，相似度指标D 的取值范围为(0,1)，D 较小时，已标记样本集信息量较少，随着迭代过程的进行，已标记样本集的信息量逐渐增加，相似度D 逐渐趋近于1，当D 连续两次大于设定的终止阈值时，则认为已标记样本集的信息量已经达到要求，迭代过程终止。

2.4 基于KELM的快速主动学习算法流程

以上从样本选择策略、迭代更新过程和终止条件设计等方面描述了所提快速主动学习方法，建模流程如图1所示，具体建模步骤如下：

（1）将原始训练集分为有标记训练集和无标记训练集；

（2）在初始化阶段，利用KELM 算法进行样本选择，选取部分样本数据进行标记，建立KELM 模型，并保存初始过程的运算信息；

（3）在迭代学习阶段，利用迭代信息和矩阵反演公式优化KELM 评估算法，选择样本数据进行标记，建立KELM 模型，并保存迭代过程的运行信息；

（4）迭代终止检验，若标记样本集的相似度指标符合终止条件，输出KELM 软测量模型，主动学习终止，否则返回步骤（3）进入新一轮的迭代。

3 仿真实验

3.1 数值仿真实验

为了验证所提方法的有效性，以二维空间为例，生成60 个服从高斯分布的样本数据，高斯分布的均值向量分别为[0,0]T,[8,0]T,[0,0]T和[8,8]T，协方差矩阵为单位阵，利用KELM 对无标记样本进行信息评估，有标记样本与无标记样本的置信度关系如图2(a)所示，其中红色实心点为已标记样本，绿色实心点为无标记样本，色标值表示KELM 进行样本评估后所得到的置信度。从图2(a)可以看出，已标记样本的附近区域置信度较高，经过KELM 样本选择和人工标记后，有标记样本和无标记样本的置信度关系如图2(b)所示，可以看出，新标记的样本能够为KELM 模型空间提供更多信息，有效扩充了模型空间，说明了本文采用KELM 的置信度指标作为样本选择评价准则的合理性。

3.2 硫回收仿真实验

为了进一步验证本文方法的性能，选用硫回收过程作为仿真对象，其简化的工艺流程如图3所示。硫回收装置(sulfur revoery unit, SRU)主要对含硫气体进行硫的回收，以防止对大气造成污染。SRU 过程的输入为两种酸性气体，一种是含有硫化氢的气体，称为MEA，另一种是含有硫化氢和二氧化硫的气体，称为SWS。MEA 和SWS 首先被送入B106、B103中进行焚烧从而除去残留的氨气，然后依次送入冷凝器和催化转化器中，催化转化器通过H2S 和SO2的反应生成硫和水，从而达到清除硫化物的目的。详细的SRU 描述可以参考文献[29]。硫回收过程含有2 个主导变量，分别为H2S 和SO2浓度，SRU的过程变量描述如表1所示。

SRU 共收集2000 组数据，从中选择1000 组数据作为训练集，1000 组数据作为测试集，训练集中初始标记样本有10 个，未标记样本有990 个，标签率为1%，迭代过程中采用KELM 方法训练模型。实验环境为64 位Windows7 操作系统，Intel(R) Core(TM)i5-6500 CPU 3.2GHz处理器，8GB内存，编程语言使用python。

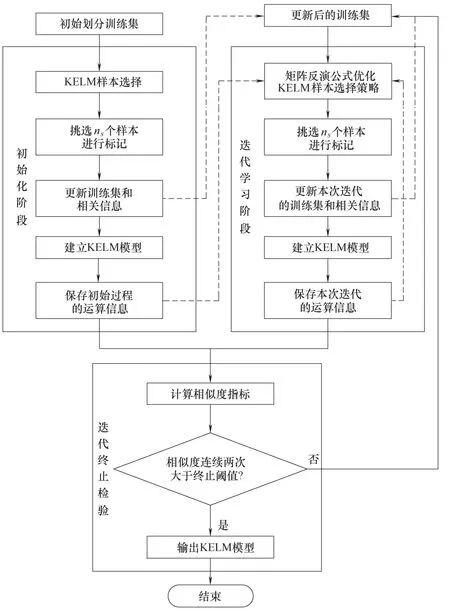
图1 基于KELM的快速主动学习算法流程Fig.1 The flow of quick active learning algorithm based on KELM

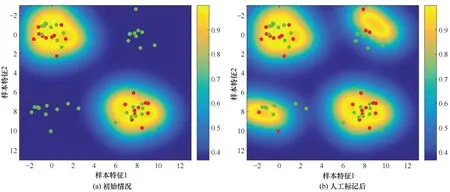
图2 已标记样本和无标记样本的置信度关系图（数值仿真实验）Fig.2 Confidence relationship between labeled samples and unlabeled samples(Numerical simulation experiment)

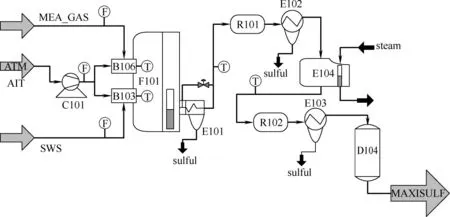
图3 SRU的简化工艺流程Fig.3 Simplified process flow of SRU

表1 SRU的过程变量描述Table 1 Process variable description of SRU

首先对所提方法的样本选择策略进行实验分析，有标记样本和无标记样本如图4(a)所示，横坐标为SRU 的u2变量，纵坐标为SRU 的u3变量，红色实心点为10 个已标记样本，蓝色实心点为无标记样本，且样本颜色随置信度的变化而变化，采用KELM算法对无标记样本进行信息评估，有标记样本与无标记样本的置信度关系如图4(b)所示，可以看出，新标记的样本与原始标记样本差异较大，能够为KELM 提供更多额外信息，有效扩充了KELM 建模空间，进一步验证了所提方法的合理性。

其次对迭代更新过程的学习步长(每次迭代标记样本个数)进行实验分析，图5 为所提方法学习步长对模型性能的影响。可以看出，随着学习步长num 的增加，更多的标记样本添加到训练集中优化KELM 模型，模型性能提升得越快，然而人工标记成本也随之增多。进一步在相同标记样本数量的情况下，重新进行仿真实验，从图6 可以看出，在迭代初期越小的学习步长对模型性能提升得越快，相应地迭代次数和运算成本也随之增多。

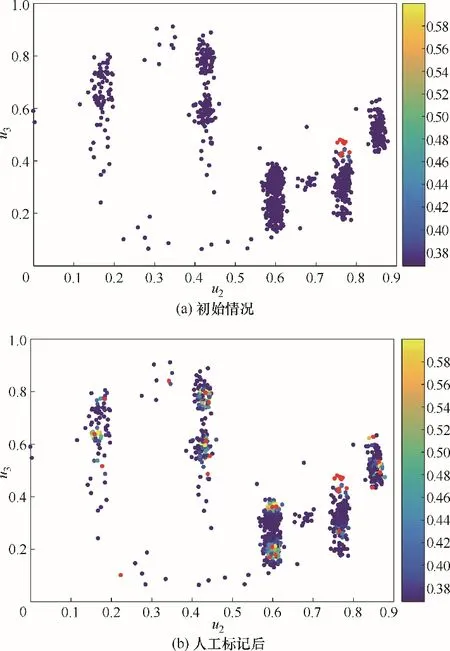
图4 已标记样本和无标记样本的置信度关系图（硫回收仿真实验）Fig.4 Confidence relationship between labeled samples and unlabeled samples(sulfur recovery simulation experiment)

图7 为无标记样本分别在第20 次、第40 次、第60 次和第80 次迭代后无标记样本置信度的变化情况，其中虚线为无标记样本置信度的平均值。可以看出，随着主动学习迭代过程的进行，无标记样本的置信度越来越大，并逐渐趋近于1。主要是因为软测量模型在迭代更新后，更多的标记样本参与到KELM 模型优化中，使得对无标记样本的信息评估更加精确。并且随着迭代过程的运行，无标记样本信息逐渐减少，KELM 模型性能不再有显著提升。

图5 在不同学习步长下模型性能随迭代次数的变化Fig.5 Change of model performance with the number of iterations under different learning steps

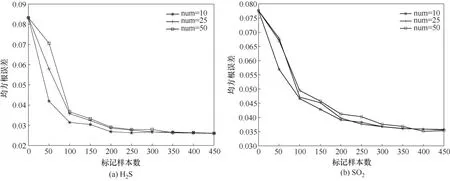
图6 在不同学习步长下模型性能随标记样本个数的变化Fig.6 Change of model performance with number of labeled samples under different learning steps

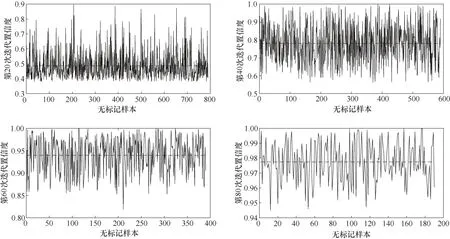
图7 无标记样本的置信度随迭代次数的变化Fig.7 Change of confidence of unlabeled samples with the number of iterations

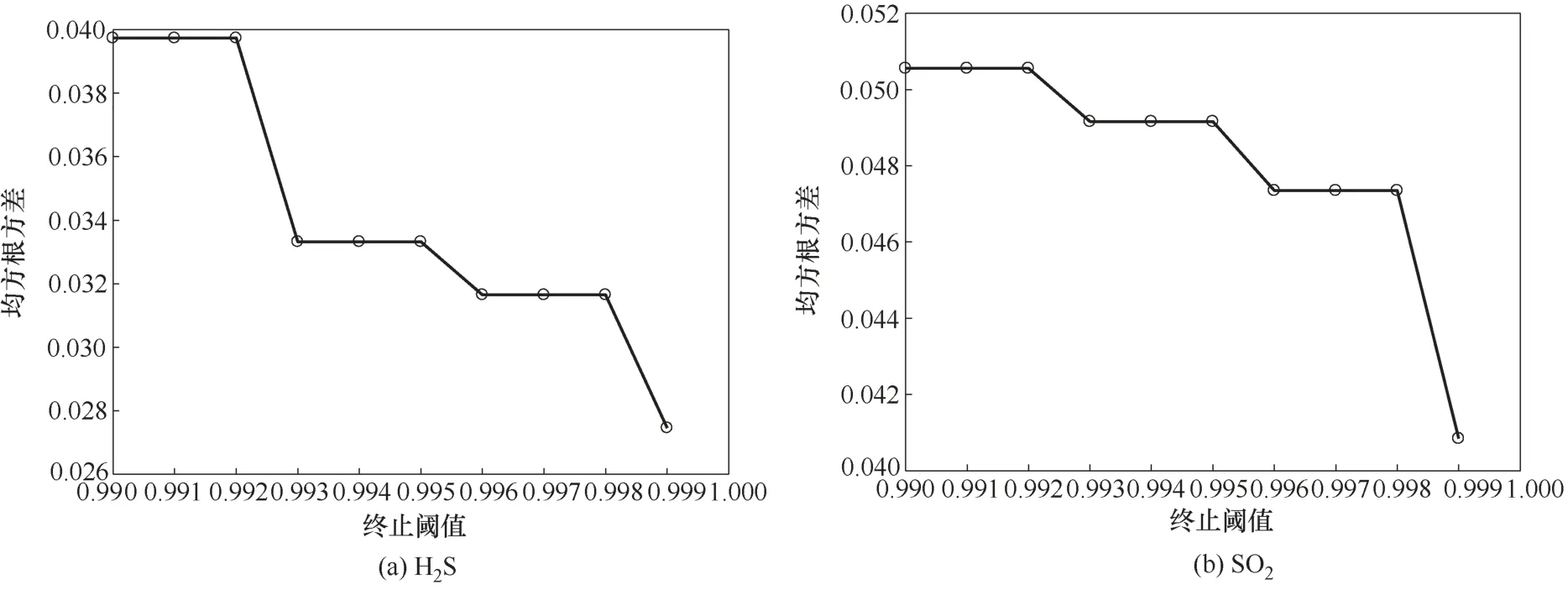
图8 不同终止阈值对模型性能的影响Fig.8 Effect of different termination thresholds on model performance

图8为终止条件中不同终止阈值对模型性能的影响，可以看出，随着终止阈值逐渐增大，模型性能逐渐提升。这是因为越大的阈值对终止条件要求越高，从而需要标记更多无标记样本来提升模型性能，同时人工标记成本和运算成本也随之增加，因此应在不影响KELM 模型性能的条件下设置尽可能高的终止阈值，本实验在预测H2S和SO2的浓度时将终止阈值设为0.999。

最后为了进一步验证所提方法的有效性，纵向比较了四种主动学习方法，对比方法包括Random、DAL[30]和RSAL[31]。

(1)Random 方法。利用随机选择的方式选取无标记样本进行标记。

(2)DAL 方法。通过计算无标记样本与有标记样本之间的欧式距离来度量无标记样本信息，从而挑选信息量较大的样本进行标记。

(3) RSAL 方法。利用已标记样本构建残差模型，并对无标记样本进行残差估计，以此挑选残差较大的样本进行标记。

将本文所提方法记为Proposed，迭代过程中的学习步长设置为10，分别进行5次仿真实验，四种主动学习方法的平均均方根误差(RMSE)随迭代次数的变化情况如图9 所示，四种主动学习方法在迭代过程中的性能指标如表2和表3所示。

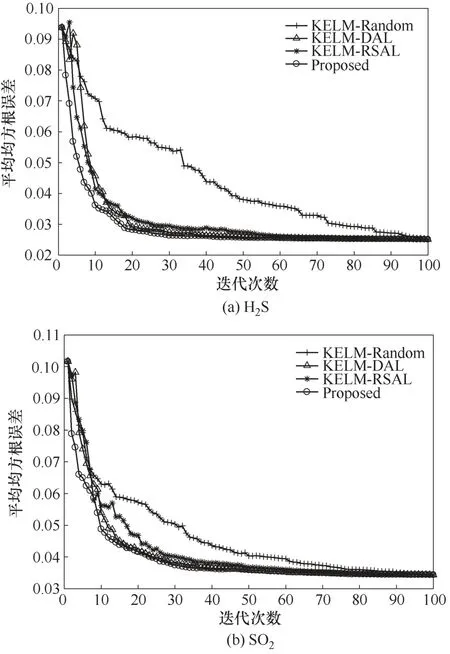
图9 平均RMSE随迭代次数的变化Fig.9 The change of mean RMSE with the number of iterations

从图9可以看出，随着标记数据的增加，四种主动学习的软测量模型性能均有所提升。其中，RSAL、DAL和本文方法均比Random方法的效果好，相比于RSAL 和DAL 方法，本文方法的收敛速度更快，这表明在相同的标记代价下，本文方法能够对软测量模型性能提升得更高，第30 次迭代后，软测量模型性能基本保持不变，为了达到相同的效果，随机选择需要标记接近3倍的无标记样本。

从表2和表3可以看出，RSAL、DAL和本文方法的RMSE的标准差均低于Random 方法，主动学习方法比Random 更加稳定，相比于RSAL 和DAL 方法，本文方法在大多情况下标准差最小，若以稳定性作为评价指标，所提方法的模型性能最好。最后，对主动学习迭代过程的运行时间进行分析，可以看出，与RSAL和DAL方法相比，所提方法的迭代更新时间最短，降低了迭代过程的运行成本，比较全面地提升了主动学习的性能。

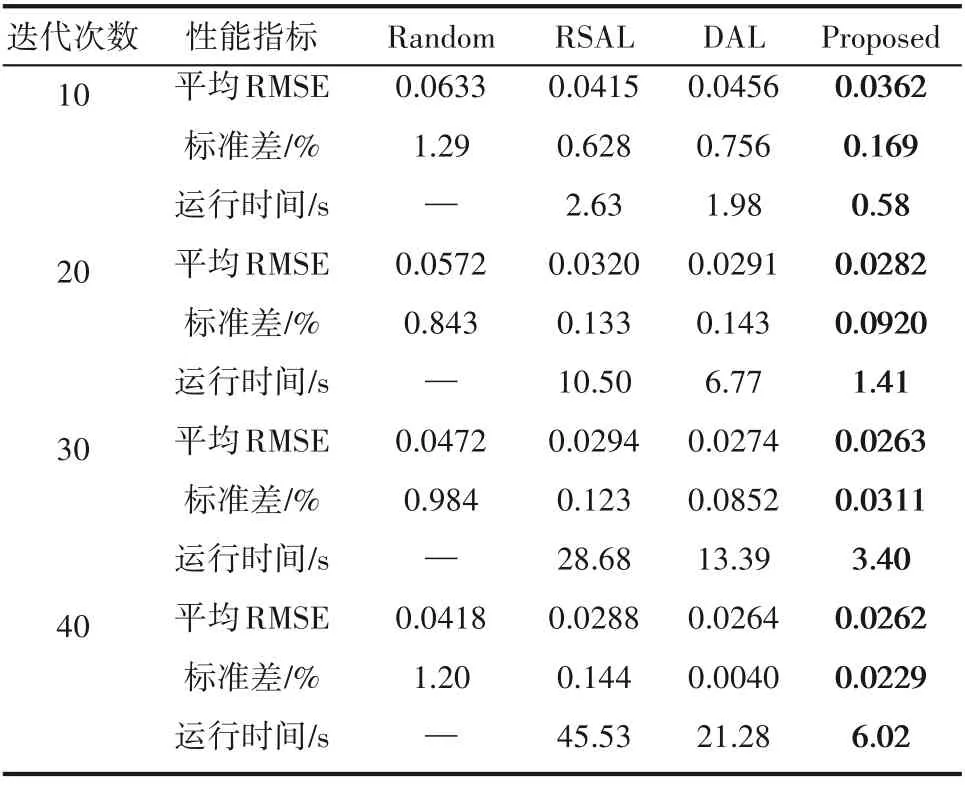
表2 四种主动学习方法在迭代过程中对H2S浓度预测的性能指标Table 2 Performance index of four active learning methods for H2S concentration prediction in iterative process

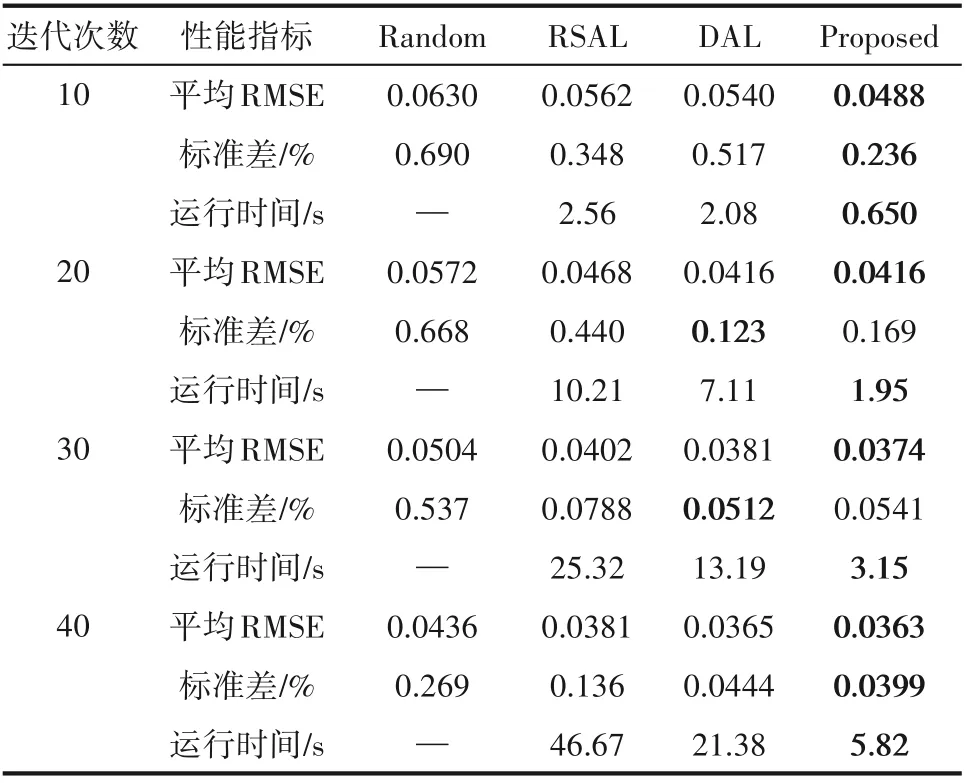
表3 四种主动学习方法在迭代过程中对SO2浓度预测的性能指标Table 3 Performance index of four active learning methods for SO2 concentration prediction in iterative process

4 结 论

针对工业过程中有标记样本少无标记样本多的情况，提出了一种基于核极限学习机的快速主动学习方法，该方法利用KELM 对无标记样本进行信息评估，根据每次迭代的运算信息优化样本选择策略，并引入矩阵相似度理论完成终止条件的设计。通过对硫回收过程H2S 和SO2浓度的测试，结果表明，所提方法不仅具有较强的样本选择能力，而且迭代更新速度较快，稳定性较高，应用于复杂化工过程建模，能够大大降低主动学习的运算成本，并减少人工标记代价，更加有效地实现过程质量变量的软测量。