好氧发酵过程微界面传质耦合模拟分析
冯尧成,任厉泰,张锋,张志炳
(南京大学化学化工学院,江苏南京210023)
引 言
2,3-丁二醇作为一种重要的化工原料和液体燃料,广泛应用于化工、能源及食品等领域[1-2],因此寻求经济、高效和低污染的2,3-丁二醇制备方式并最终将其产业化一直是科学研究的热点[3]。相较于传统化学法生产2,3-丁二醇,微生物发酵法因其工艺条件温和、操作简便、成本低廉的特点,优势明显[4]。虽然目前国内外的一系列研究都能达到相当高的糖转化率,但这些成果大多数都建立在消耗高葡萄糖含量的精细底物淀粉的基础上,不利于2,3-丁二醇的大规模发酵生产。如何利用廉价糖源达到较为良好的发酵效果是当今面临的难题[5]。微生物好氧发酵过程是一种典型的多相反应体系,该体系在化工、能源、环保等多个领域都有广泛的运用,但无论是传质分离过程还是化学反应过程,多相之间物质传输的速率都是制约反应速率和物质利用率的关键因素[6-9],其根本原因在于气液或气液固之间的相界面积太小[10]。而在微生物发酵生产2,3-丁二醇的菌种生长阶段,恰好需要较高的溶氧量来支持菌体的代谢[1]。微界面强化传质技术通过界面传质强化来实现过程强化。基于微界面强化理念,研究者开发了一系列新型高效的反应装置,并成功应用于工业过程[11-14]。
微生物发酵过程中,气泡是气液间物质传输的重要载体,其在液层中的运动与传质过程直接决定了微生物发酵工艺过程的效率[15-16]。而对于单气泡而言,其半径决定了它的运动速率[17],半径的变化受物质传输与气泡内压的控制,而传质速率又会受到运动速率与气泡尺寸的显著影响[18-19],显然,气泡的上升与传质是一个互相影响的耦合过程。因此,建立合适的数学模型,描述气泡在体系内上升与传质的过程,并与微界面强化技术相结合,对发酵罐的设计以及发酵工艺中的各种工况与参数的设定都有非常有意义的指导作用。本文在这一背景下,构建多组分气泡运动与传质耦合模型,并结合能量耗散理论,利用数值模拟的方式分析微界面体系对好氧发酵的强化过程,并选择预设工况下的优化参数。
1 模型介绍
1.1 气泡上升与传质耦合模型
田恒斗等[20-22]结合气泡瞬态加速度模型与气泡瞬态非平衡传质模型,以描述单组分气泡在液体中的上升和传质作用,其核心方程组如下:

其中第一个方程是描述气泡瞬态加速度的微分方程。第二个是描述气泡瞬态传质的微分方程,CA为液相中的气体浓度,CI为气液相界面处的气体浓度。第四个是利用非平衡传质理论求解CI的公式,C*为气液界面处气体的平衡浓度,H 为气体的溶解度系数,σ为液体的表面张力。
1.2 多组分气相在混合溶液中的上升与传质耦合模型
在工业过程中,多组分气体构成的反应体系较为常见,特别是以空气为反应物的,如好氧发酵、PX氧化、湿式氧化等过程。多组分气体传质与反应过程中存在组分间的竞争与协调关系,并影响传质与反应过程。因此,构建气泡运动传质耦合模型,以适用多组分气泡在液体中的运动和传质行为,具有更为重要的工业意义。
在含N 个组分的气泡和K 个组分的液相体系中,令yi为气相i 组分的摩尔分数,ρi为气相i 组分的密度,Mg,i为气相中i 组分的摩尔质量,yl,i为液相i 组分的摩尔分数,μi为液相i 组分的黏度,Ml,i为液相i组分的摩尔质量,可得到一系列数组:

因此,混合气体的密度可由式(8)计算:

混合液体的黏度μl[23]可表示为:
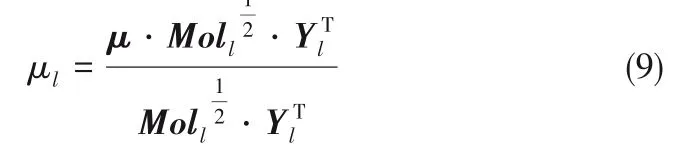
通过这一系列扩展过程,可以用式(10)取代式(1)中第一行的微分方程,使描述气泡瞬态加速度的方程适用于多组分。
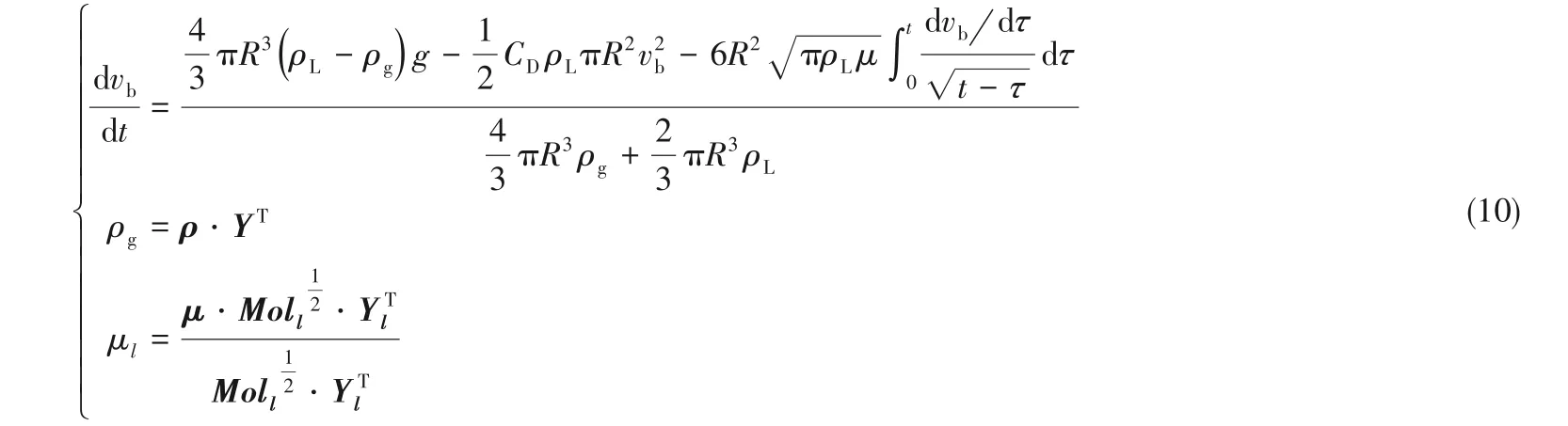
为了简化问题,假设气相各组分在边界层的传质是互不干涉的,则单个气泡的物质传输速率可表示为:

式中,DAB为气体在液相中的扩散系数,I =[1 1 … 1]。
任意时刻气泡内所含气体质量可表示为:

式(12)两边对时间t求导可得:

对于包含N个组分的气泡,代入式(8),则有:
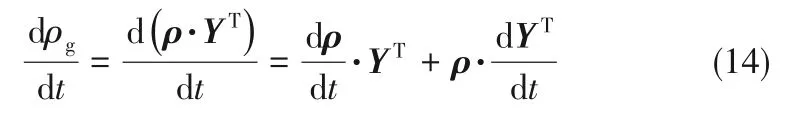


设mg,i为气泡中i 组分的质量,Mg为该参数的合集数组;再设Ng=[n1n2… nN],ni是气泡中i组分的物质的量;因为Ng= Mg/Molg,所以:

将式(10)、式(11)代入式(7)可得:



用式(19)取代式(1)中第二行的微分方程,同样使描述气泡瞬态非平衡传质的方程适用于多组分气泡。
1.3 能量耗散模型
能量耗散率(energy dissipation rate,ε),定义为单位质量流体耗散能量的速率,单位为W·kg-1。基于本课题组前期对于微界面强化技术的研究[24-25],在超细气泡控制塔中,气泡产生过程中的能量耗散速率与气泡体系的尺寸有很大的关系。可以用ε来表征微气泡体系的能量消耗情况,其与气泡尺寸的关系如下:
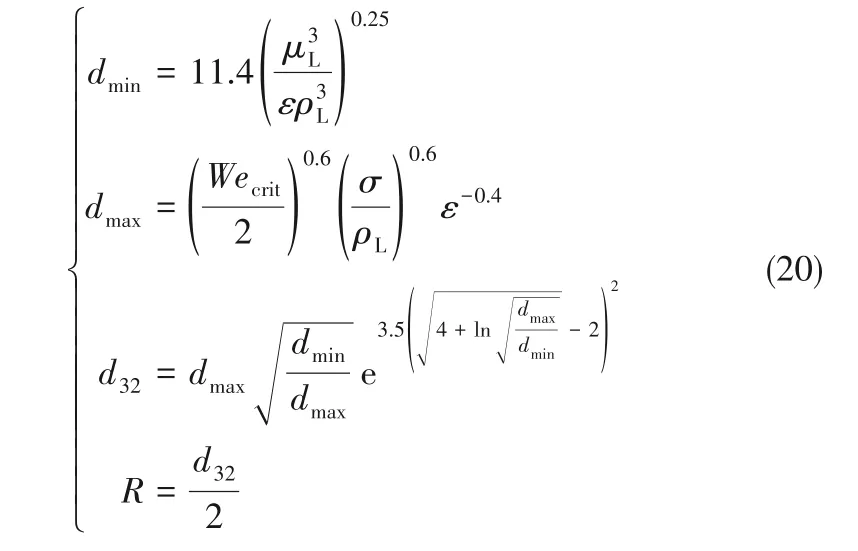
式中,dmin和dmax分别代表体系中最小和最大的气 泡 直 径;d32为 气 泡 的Satuer 直 径;Wecrit为 临 界Weber数,通常取1.24[26]。
2 模型计算方法
本文利用Runge-Kutta 变阶方法[27-28]进行上述模型(ODE 系统)数值模拟。Runge-Kutta 变阶方法是基于Runge-Kutta 定阶方法改进的数值积分方法。对改进后的式(1)使用该方法,引入初始条件,并输入所需参数,即可对任意t 时刻对应的气泡半径、上浮速度、所在位置以及瞬时传质速率等参数实现快速数值求解。
3 计算实例与结果分析
模拟好氧发酵体系中微气泡的上升运动及氧传质情况,并调节关键参数,分析体系的传质与能耗情况,从而获得较为理想的工况。空气主要由氧气和氮气两种气体组成,模拟计算中所用到的该两种物质的相关参数如表1所示。
计算过程中用到的其他条件包括:微生物发酵过程的操作压强为一个标准大气压(101325 Pa),温度为20℃。液相密度ρL为1000 kg·m-3,液体的表面张力σ 为0.0728 N·m-1,动力黏度系数μ 为1.021×10-3Pa·s,液相气体浓度CA=0,发酵罐液面高度为5 m。微界面强化的核心思想即利用微界面取代传统的宏界面,从而成倍地提高传质速率,根据微界面的定义[8]选择一系列初始气泡半径R0(0.1,0.3,0.5,0.8,1.0,1.5,2.0 mm)来考察微界面体系对传质效果的提升。初值条件设为气泡高度h0=0,气泡初始速度vb0=0。预设的运动时间为50 s。

表1 体系中主要物质的各项参数Table 1 Parameters of main substances in the system
3.1 气泡运动状态
气泡半径是决定其运动与传质状态的关键参数[29],气泡上升过程中,其大小会受到气体传输和气泡内压的制约。
如图1 所示,气泡上升过程中,其半径逐渐减小,这种气泡尺寸的变化主要是气液两相间传质造成的,且初始半径越大的气泡尺寸变化越显著。另外大气泡由于运动速度较大,能够在短时间内迅速离开液层。气泡上升高度以及上升速率的变化情况分别如图2、图3所示。

图1 气泡半径随时间的变化情况Fig.1 Change of bubble radius with time

图2 气泡高度随时间的变化情况Fig.2 Change of bubble height with time

图3 气泡速率随时间的变化情况Fig.3 Change of bubble velocity with time
在图2 中,实心点所代表的气泡在设定的上升时间内会离开液面,而空心点表示的气泡在预设时间内将一直停留在液层内,由此可知,较小的气泡所构成的微界面体系可充分利用罐体高度,长时间停留在液层中,实现了充分传质,而较大的气泡极可能未达到充分传质前已从液体中逸出,导致物料的浪费。气泡半径是决定气泡运动速率的关键因素,因此,气泡上升速率变化的趋势应当与气泡半径变化的趋势相吻合,结合图1 与图3 来看,这二者之间变化的趋势是符合预期的。
3.2 气泡传质情况
气泡内的主要组分为N2与O2。由于气泡大小对于气液传质界面有较大的影响,为了评价各不同尺寸气泡的传质效果,引入传质通量(mass transfer flux,J),定义为单个气泡中的某组分在单位时间内的质量变化量与该时刻气泡表面积的比值。此外,氧气利用率(O2utilization,η),即传输至液相中的氧气质量占气泡中原有氧气质量的比值,也是衡量传质效果的重要指标。两种指标的具体计算公式如下:
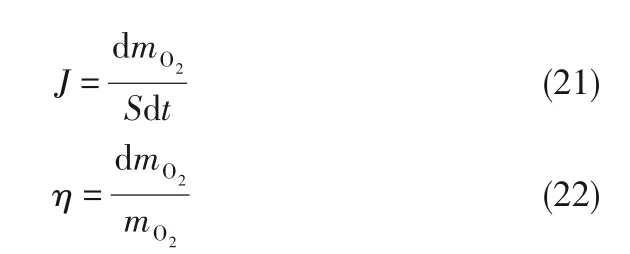
式中,S为t时刻气泡的表面积。
以初始半径为0.5 mm 的气泡为例,表2 展示了气泡内两种气体的组成变化,图4 为其传质通量的变化。
由表2 可知,气泡内的气体组成随气泡的运动与传质而改变,N2所占的摩尔分数略有上升,O2的摩尔分数下降,这是由于两者扩散差异所致。但O2在液相中的扩散系数也仅是略高于N2,因此在传质速率上不会存在过大的差异。这在图4 也有所反映,从整体趋势上来看,两种气体的传质通量变化趋势几乎一致,但N2的传质通量要明显高于O2。这是因为在空气中,N2的物质的量几乎是O2的四倍,其在界面处存在更高的相界面浓度,从而导致更高的传质通量。但在实际的好氧发酵过程中,液相溶解的N2不被消耗,故存在传质平衡,而氧气会被不断消耗。

表2 气泡内气体摩尔分数的变化Table 2 Changes of gas mole fraction in bubbles

图4 两种气体传质通量随时间变化的情况Fig.4 Change of mass transfer flux of two gases with time
对比不同大小气泡中O2的传输效率是选择合适初始气泡半径的关键步骤。

图5 初始半径对O2传质通量的影响Fig.5 Effect of initial radius on mass transfer flux of O2

图6 初始半径对O2利用率的影响Fig.6 Effect of initial radius on O2 utilization
由图5 可知,气泡中氧的传质速率会迅速上升达到一个极值,而后缓慢下降。对于小气泡,这种降低越慢,而且气泡越小,能达到的传质通量极值就越高,这充分体现了微界面体系对气液传质的强化特性。这得益于小气泡较小的上升速率和较薄的传质边界层。而对于整个体系而言,较小的气泡群会拥有更大的相界面积[30],从而提高体系的气含率和氧传质速率,对发酵过程同样也能起到促进作用。
就物料成本考虑,大气泡的携带氧气能力强,处理量大,但传质通量较小。如图6所示,其传输到液体内的O2占其原携带O2量的百分比明显小于小气泡;另外大气泡上升速度快,停留时间短,也制约了O2在气液间的传输。
溶解氧(dissolved oxygen,DO)在发酵工艺中一般以相对含量表示,称为DO 值,是发酵过程中的一项重要指标。一般认为N2吹扫后体系中的DO 值为0,而将氧气充分溶解之后的DO 值视为100%。由于好氧发酵过程的各个阶段存在不同的DO 值,研究DO 值对O2传输的影响也是必要的,根据非平衡理论计算所得的液相浓度CA与传质推动力CA-CI的关系如图7所示。显然,随着CA的增大,传质推动力先增后减,存在最大值。
为了便于表达,设XA为液相中的气体浓度与该条件下液相饱和浓度的比值,称为液相饱和度,XI为界面浓度与饱和浓度的比值,称为界面饱和度,两者之差即为该条件下的传质推动力,从图8 中可以看出,当液相饱和度在0.2~0.3 时,传质推动力有最大值。以初始半径为0.3 mm 的气泡为例计算,考察不同DO 值下的传质通量与氧气利用率,得到的图9、图10可以表明,计算结果与预测结果一致,当DO值为20%时,有最好的传质效果; 当DO 值达到100%之后,传质即停止,甚至会出现“倒吸”现象。
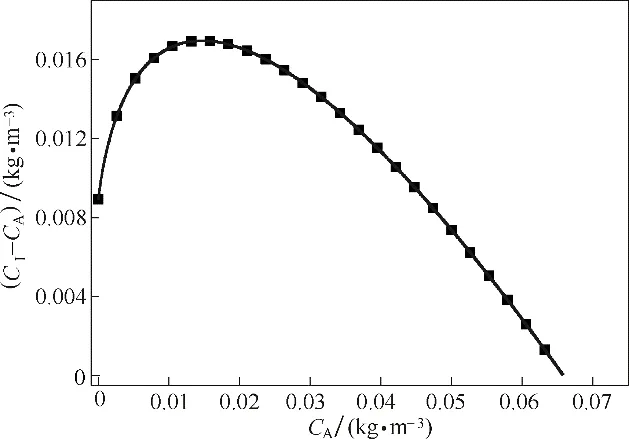
图7 不同液相浓度下的传质推动力Fig.7 Mass transfer driving force under different CA

图8 液相饱和度对传质推动力的影响Fig.8 Effect of XA on the mass transfer driving force

图9 DO值对O2利用率的影响Fig.9 Effect of DO value on O2 utilization
3.3 微气泡体系的能耗
如前文所述,微气泡在促进气液传质方面的作用显著,但要形成小气泡往往需要较高的能量消耗[31]。实际生产过程中不仅需要考虑物料成本,能量的损耗同样也需要计算。
图11展示了O2传质效率、能量耗散系数与初始气泡半径之间的关系。由图可知,较高的传质速率与较低的能耗难以兼得,但一定存在某个区间,在能耗适中的情况下,获得较为理想的传质效果。在图11中,这个区间应该在250 ~500 μm之间。
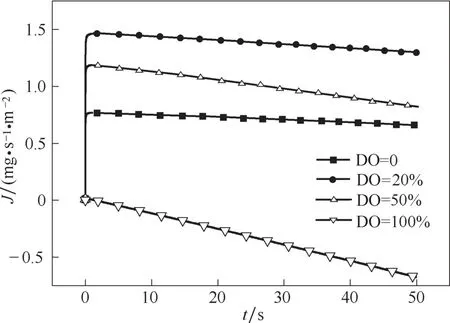
图10 DO值对O2传质通量的影响Fig.10 Effect of DO value on mass transfer flux of O2

图11 不同的初始半径对传质以及能量耗散系数的影响Fig.11 Effect of different R0 on mass transfer and energy dissipation coefficient
但是,本文的研究还是在一个高度理想化的情况下进行的,气泡在水平方向上是否会有运动,多气泡之间的互相作用等一系列的问题都需要进一步的研究,现有的理论成果是否可靠也有待实验的论证。
4 结 论
针对好氧发酵过程,本文将原有单组分气泡上升与传质模型扩展到多组分气泡传质过程,考察气泡的不同初始半径对不同组分传质的影响,结合能量耗散系数这一指标,评估体系的能耗情况,选择出理论条件下较为合适的工况条件。
计算结果表明,当在20℃,1 个标准大气压(101325 Pa)的标准状况下操作时,对于一个液面高度为5 m的发酵罐,当气泡初始半径超过0.5 mm时,其将在较短时间内逸出体系,造成物料浪费;较小的气泡则拥有更好的传质效果,当气泡初始半径小于0.1 mm 时,其对携带的O2的利用率可以接近50%,显示了微界面体系对于气液传质的强化特性。
DO 值是好氧发酵工艺中的一项重要指标,通过模型的预测,在预设工况下,将体系内的DO 值维持在20%~30%之间时,会取得较为良好的传质效果。
由于产生微气泡的能耗需要较高的能耗,因此一味地追求小气泡并不能保证经济效益。在不同工况下,综合考虑物料成本和能耗成本,选择合适的分散尺寸才能带来最佳的优化效果。
符 号 说 明
C——气体溶解于液相中的浓度,kg·m-3
C*——气液界面处的平衡浓度,kg·m-3
CA——液相主体中的气体浓度,kg·m-3
CD——黏性阻力系数
CI——气液界面处的气体浓度,kg·m-3
DAB——气体分子在液体中扩散速率,m2·s-1
dmax——气泡群中气泡的最大直径,m
dmin——气泡群中气泡的最小直径,m
d32——气泡群的Sauter直径,m
E——亨利系数,kPa
g——重力加速度,N·kg-1
H——溶解度系数,kg·m-3·Pa-1
h——气泡上升高度,m
J——传质通量,kg·s-1·m-2
M——摩尔质量,g·mol-1
Mg——组分质量合集数组,kg
Mol——摩尔质量的合集数组,g·mol-1
mg——气泡质量,kg
mO2——气泡内氧气质量,kg
N——物质的量合集数组,mol
patm——体系外界压强,Pa
pg——气泡内部压强,Pa
R——气泡半径,m
S——气泡表面积,m2
t——气泡上升运动时间,s
Vg——气泡体积,m3
vb——气泡上升速率,m·s-1
Wecrit——临界Weber数
XA——液相饱和度
XI——界面饱和度
Y——组分摩尔分率的合集数组
y——组分摩尔分数
ε——能量耗散率,W·kg-1
η——氧气利用率,%
μ——动力黏度系数,Pa·s
ρg——气泡内气体密度,kg·m-3
ρL——液体密度,kg·m-3
ρ0——外界压强下对应气体的密度,kg·m-3
σ——表面张力,N·m-1
下角标
g——气相
l——液相
0——初始值

