湿气管道积液临界气速预测的新模型

李国豪，邓道明，宫敬

（中国石油大学（北京）油气管道输送安全国家工程实验室，石油工程教育部重点实验室，城市油气输配技术北京市重点实验室，北京102249）

引 言

国内外天然气集输经常采用湿气集输的方式。Meng[1]指出标况（101.3 kPa, 15℃）下液相体积流量与气相体积流量之比小于1100 m3/106m3时为低液相负荷流动。湿气管道一般为低液相负荷流动，例如，我国某页岩气田湿气管道气液分离之前的平均液相负荷一般为200 m3/106m3左右，最大的平均液相负荷为1000 m3/106m3。但是即便液相负荷如此低和井场集气站进行了气液分离，该页岩气田的一些气井和早期集输管线仍存在较严重积液问题。

早期的一些学者认为，低液相负荷下天然气两相管流为弥散雾状流，即认为低液相负荷流动不会产生严重积液现象。例如Adewumi 等[2]在美国国家自然科学基金、工程基金和气体研究所(GRI)的资助下，对低液相负荷天然气-凝析液管流进行了一系列研究，其模拟计算理论主要基于漂移的弥散雾状流模型。但是其模型计算结果没有得到实验或生产数据的广泛支持。显然湿气管道的弥散雾状流模型难以解释经过分离器分离的湿气在下游集输管道里仍然积液严重的原因。

正常情况下，湿气管道内低液相负荷的流动为气液两相分层流。当气田开发初期开井数较少或气田开发后期气井产量较低时，集输管内气体流速较低，如果气相对液相的拖曳力不足以拖动液相向前流动，气液分层流便开始变得不稳定，最终液体会在上倾管道低洼处积集，积液现象因此产生。另外过大的集输管道直径也会引起积液。本文将上倾管道液膜不稳定的最大气相表观速度（或者说液膜稳定的最小气相表观速度）作为临界气速。工程实践表明，起伏的湿气集输管道积液是普遍现象。

湿气集输管道积液的存在会导致诸多风险：（1）诱使管内产生内腐蚀，进而影响生产运行[3]；（2）集输管道积液意味着存在更大的相间滑脱损失，这会导致井口回压增加，从而降低气井产量，甚至可能造成气井积液；（3）集输管道积液还伴随着管道集输效率降低、超压安全风险、下游处理量不稳定等问题。因此，研究湿气管道的积液对集输管道的设计和运行都具有重要的指导意义。

1 积液预测模型评述

一些学者采用商业多相流软件OLGA 对湿气管道进行积液研究。例如刘建武等[4]、张爱娟等[5]建立起伏的集输管道的OLGA 计算模型，经过OLGA 计算获得了管道全线的积液量等相对宏观的参数。但是，OLGA 软件作为一个黑箱，使用者并不知晓其具体的计算模型和方法，难以利用OLGA 建立积液机理计算模型。

目前主流的积液机理模型有最小压降模型、持液率突变模型、零液壁剪切应力模型和最小界面剪切应力模型4种。

1.1 最小压降模型

最小压降模型是指：逐渐减小气相流量，当气液两相管流的总压降最小时，管内由摩阻压降主导转换为重力压降主导，管内发生积液。Belt[6]、Yuan等[7]均支持该模型。Fan 等[8]的实验也表明，当水平倾角大于5°时，最小压降与临界气速相对应。

但是，最小压降并不能完全解释积液的机理。尽管临界气速测量方法相同，Alsaadi 等[9]和Wang等[10]的实验结果却截然不同：Alsaadi等[9]的实验管径是76.2 mm，在实验中观察到最小压降对应的气速要小于临界气速；Wang 等[10]的实验管径是30 mm 和40 mm，实验结果却显示最小压降对应的气速要略微大于临界气速。这表明最小压降可能与临界气速并不完全对应。Skopich 等[11]也观察到最小压降有时存在于稳定流中，有时又存在于不稳定流中。

1.2 持液率突变模型

对于近水平气液两相流流动，仅改变气相流量，由动量方程计算出的持液率可能会如图1所示。图1 中阴影区域对应的持液率有多个，学术上将该区域称为持液率多解区。许多学者从持液率解稳定性的角度对多解区进行研究：Landman[12]利用KH 波理论对界面波稳定性进行分析，得出持液率的高解是不存在的，中间解可能存在，低解是始终存在的；Barnea 等[13]在Landman[12]的基础上考虑了分层流的结构稳定性，指出中间解不满足结构稳定性，只有最低解是稳定的。这表明在图1多解区的左边界处，持液率由A点突变到B点。

Espedal[14]、Langsholt 等[15]、Kjolaas 等[16]、Fan[17]均在实验中观察到了持液率突变现象。Biberg 等[18]将分层流持液率突变点作为临界积液点。沈伟伟[19]综合采用“最小滑脱”准则和分层流多解方法判断持液率突变，从而计算相应的临界气速。该模型的缺点是适用范围可能较窄，因为当管道倾角和液相负荷较大时，持液率可能不突变。

图1 持液率多解区Fig.1 Regional schematic diagram for multiple liquid holdup solutions

1.3 零液壁剪切应力模型

零液壁剪切应力模型最早由Turner 等[20]提出，其认为环状流液膜转向的临界状态是液壁剪切应力为零，将液壁剪切应力为零的状态作为气井积液的临界点；然而他们认为零液壁剪切应力模型的预测值与现场数据不符，采用液滴模型预测临界气速。

Fan[17]将该模型引入近水平管的分层流模型，将液膜最底部的壁面剪切应力为零作为积液的临界判据。Alsaadi[21]在Fan[17]的基础上进行简化，将液膜的平均壁面剪切应力为零作为积液的临界判据，进而把混合动量方程中的气速和持液率解耦，节约了计算时间。若将分层流的液膜单独作为分析对象，气液界面剪切应力是主动力，液壁剪切应力是被动力，液壁剪切应力为零是液膜转向的现象，其转向的本质原因是气体携带能力不足，从界面剪切应力的角度出发能够进一步揭示积液的原因。

1.4 最小界面剪切应力模型

Barnea[22]提出了垂直管环状流的最小界面剪切应力模型，其假设环状流液膜沿管道周向均匀分布，得出对于一定的液相表观速度，界面剪切应力仅为液膜厚度/持液率的函数，如图2 所示。图2 中界面剪切应力曲线存在最小值，Barnea[22]认为在最小界面剪切应力左侧的环状流是稳定的，其右侧的环状流是不稳定的。Luo 等[23]和Shekhar 等[24]均认为液膜沿管道周向均匀分布的假设并不合理，并做了相应修正：Luo等[23]用管道底部的最大液膜厚度进行计算；Shekhar 等[24]根据Paz 等[25]的实验数据，考虑了最大液膜厚度与平均液膜厚度的关系，最终通过平均液膜厚度求出临界气速。沈伟伟等[26]在Shekhar等[24]的研究基础上考虑了液滴夹带的影响。

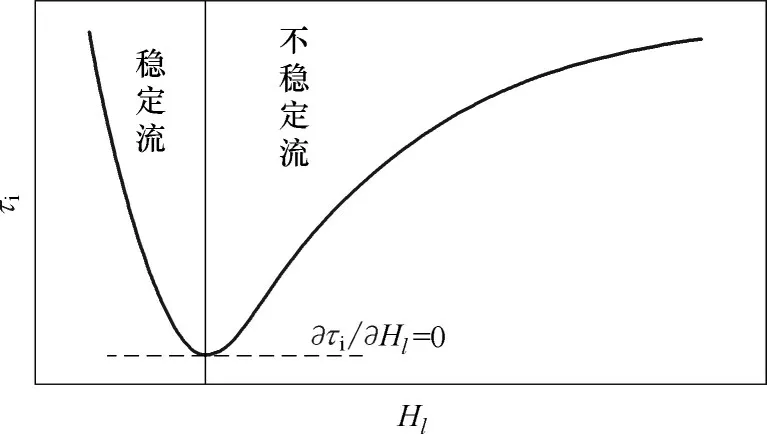
图2 最小界面剪切应力示意图Fig.2 Schematic diagram of minimum interfacial shear stress

Brito[27]将最小界面剪切应力模型从环状流扩展到了分层流，并认同最小界面剪切应力左侧对应稳定流，右侧对应不稳定流的观点。本文对稳定区与不稳定区的划分也是如此。Brito[27]通过穷举的算法寻找最小界面剪切应力对应的临界气速。 Brito 模型的不足是通过Blasius 经验关系式来计算液壁剪切应力，因为Kowalski[28]测量气液两相分层流壁面剪切应力的实验显示：气壁剪切应力与Blasius 关系式吻合得较好，但液壁剪切应力与Blasius 关系式明显不符。

2 模型建立

Langsholt 等[15]气液两相流的实验显示：气液界面波在高气速下是3D小尺度波（滚波），随着气速减小，界面波的波幅逐渐变大，依次出现2D 短波和2D长波，最终流型由分层流变为假段塞流。Fan 等[8]将实验中出现的分层流流型分为孤波（光滑分层流）和滚波两种，孤波在高气速下出现，滚波在接近流型转变时出现。Alsaadi[21]的实验中所有的分层流均是滚波分层流和长波分层流，长波分层流在接近流型转变时出现。以上实验现象均表明分层流在失稳过程中，界面波的波幅会变大。

可以推测，积液和界面波的变化有关，界面波的变化又直接与界面摩擦因子和界面剪切应力相联系。可以认为积液是由于气相给予液相的拖曳力不够，即认为气液界面剪切应力为最小值时为积液临界状态。

石油工业湿气管道的管径一般在2"以上，例如我国某页岩气开发采气管线公称直径为DN65，湿气集输管道的最大管径为DN550。Fan[29]在3"管道的低液相负荷气液两相流动的实验中观察到气液界面是接近水平的。邓道明等[30]曾建立高压大管径天然气两相流动计算模型，通过将模型计算结果与生产数据比较，认为平界面分层流模型与高压大直径天然气管道工艺计算更为贴合。这里假设分层流的界面为水平界面，即管道横截面液膜分布如图3 所示。利用Biberg[31]基于双极坐标系导出的液相速度分布解析式，将分层流界面剪切应力最小作为积液判据，建立新的湿气管道积液预测模型。

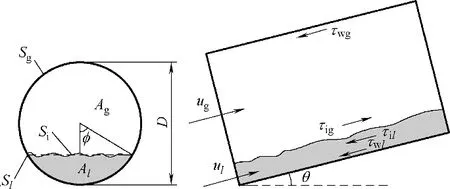
图3 湿气管道内分层流液膜分布Fig.3 Film distribution of stratified flow in wet gas pipeline

2.1 动量方程

由于分层流流型是典型的分离流，故采用经典的双流体模型；该模型的主要特点是考虑了相间的相互作用力。气、液相的动量方程为：

式中，下角标g 和l分别代表气相和液相，i表示界面；几何参数A 代表各相所占管道的横截面积，S代表各相的湿周；剪切应力τw表示各相壁面剪切应力，τi表示界面剪切应力；dp/dz表示各相沿流动方向（管道轴向）压力梯度；ρgsinθ 表示各相重力沿轴向的分力。

2.2 分层流液膜区液相流量公式化

由于湿气管道气液两相流动是低液相负荷的流动，其液相Reynolds 数一般要比转捩Reynolds 数（Re=2000）低，因此其液膜流动可认为是层流。Biberg[31]曾基于双极坐标系，假设气液两相分层流的气相为湍流、液相为层流、气液界面为平界面，并且假设气液界面上的剪切应力均匀分布，利用N-S 方程推导出了双极坐标系下液膜区的速度分布。对液膜区的液相速度求面积分，可以得到液相流量：

φB(φ)和φi(φ)是液面角φ 的函数。如图4 所示，当φ∈[0,π/2]时，φB(φ)和φi(φ)均单调递增，且当φ→0时，φB(φ)和φi(φ)→0。

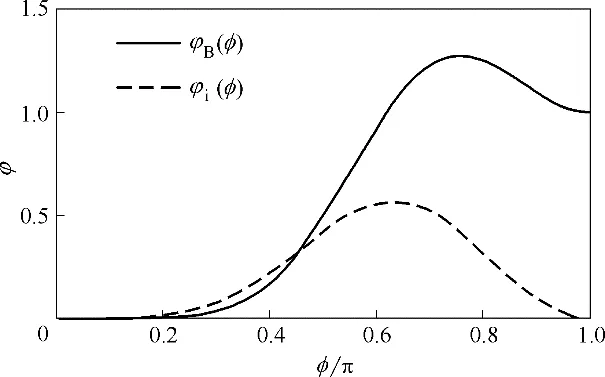
图4 权函数φB(φ)和φi(φ)Fig.4 Weight functions φB(φ)and φi(φ)

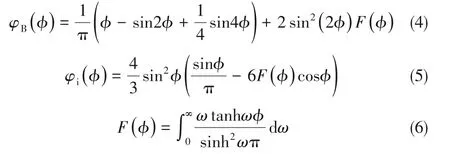
2.3 界面剪切应力

忽略液相断面上由位置高度的变化而引起的压力梯度，则气、液两相的压力梯度dp/dz应相等，将式(3)代入气相动量方程式(1)，可以得到界面剪切应力τi与液面角φ和气壁剪切应力τwg之间的关系：

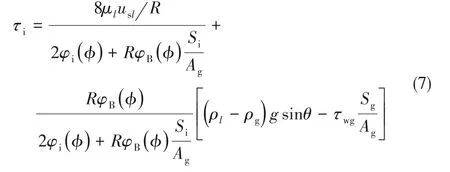
式中，气壁剪切应力τwg的计算式为式(8)，其中气壁摩擦因子fg的计算采用Blasius关系式[32]。

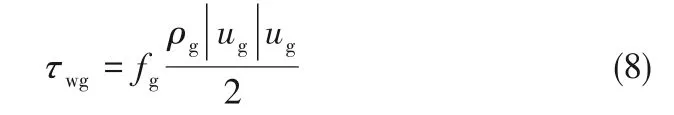
将式(8)代入式(7)，并利用Biberg[31]推出的液面角φ与持液率Hl的显式表达式，得式(9)

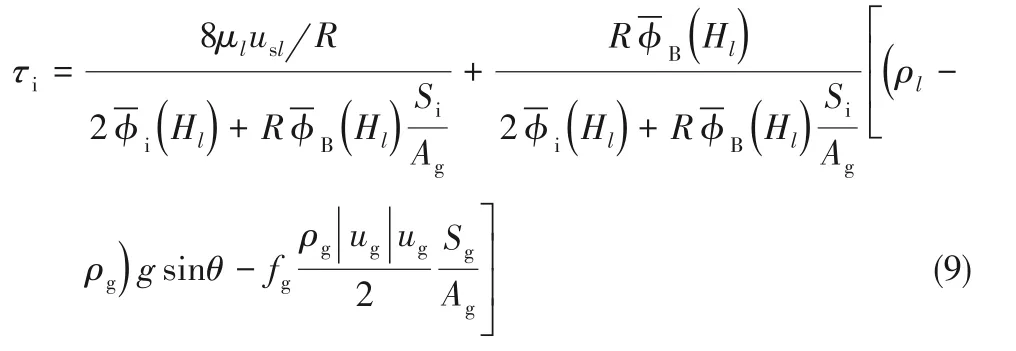
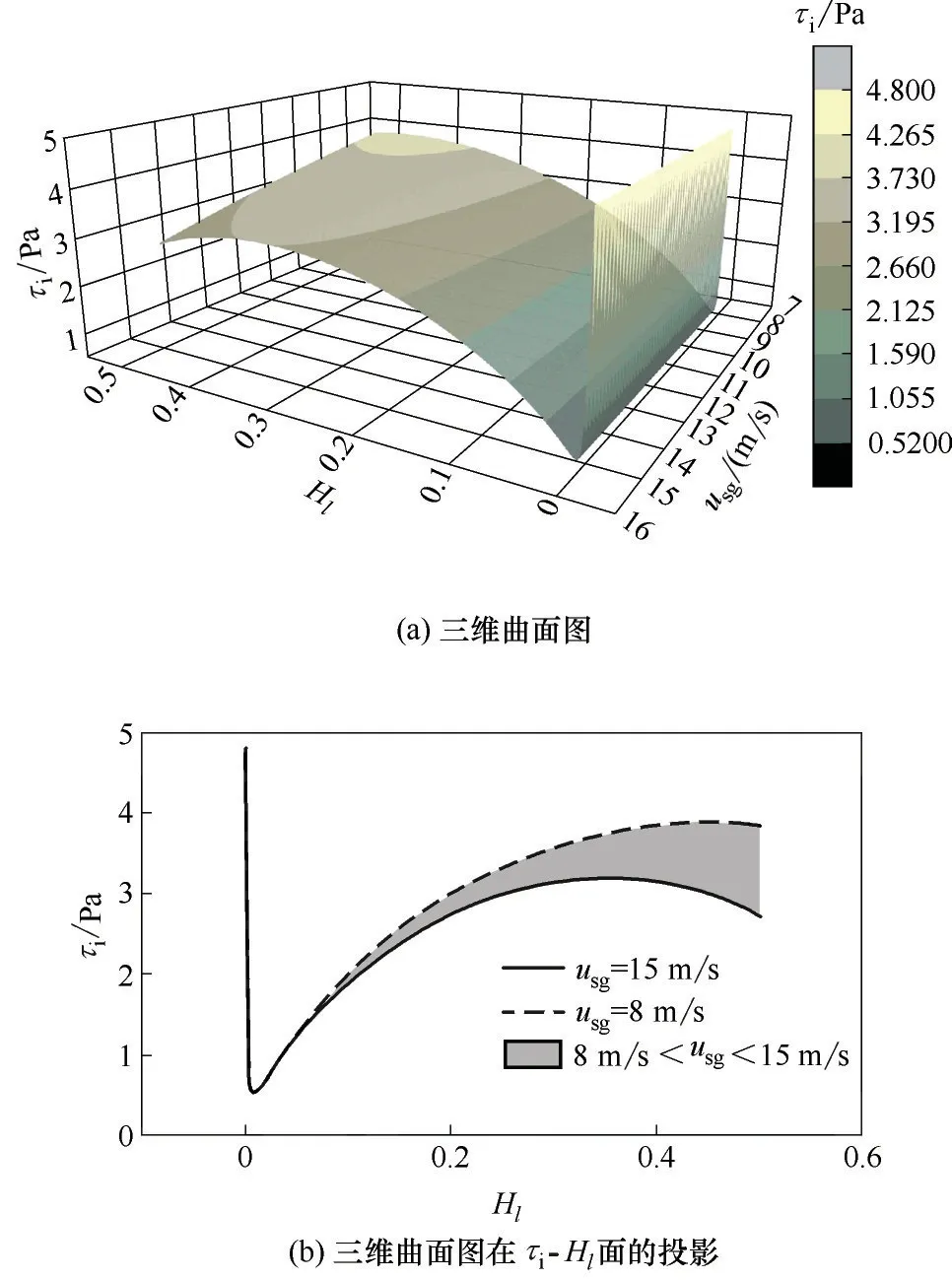
图5 τi与Hl和usg的关系[式(9)]Fig.5 Interfacial shear stress τivs holdup Hl and superficial gas velocity usg[Eq.(9)]

表1 3″上倾空气-水管道积液实验基本参数Table 1 Air-water experimental parameters in 3″upwardly inclined pipeline

由式(9)可知，当D、θ、ρg、ρl、usl已知时，τi仅是Hl和usg的函数；图5 为在表1 参数下τi与Hl和usg关系的曲面图，工程上湿气集输管道因其较低的液相负荷，气液界面剪切应力与持液率和气相折算速度关系也基本如图5 所示。由图5 可知，当usg不变、Hl∈[0,0.5]（即φ∈[0,π/2]）时，由于式(9)等号右边第一项随Hl的减小而递增，第二项随Hl的减小而递减，使得图5 呈现下凹的特性，在极值点∂τi(Hl)/∂Hl=0 处取得最小界面剪切应力τi_min，对应的持液率称为临界持液率Hl_c。另外，从图5 中可知，Hl_c对usg的变化不敏感（图中与usg轴基本平行的深色带区域），这为后续快速求解临界气速创造了条件。

τi还可通过封闭关系式(10)得出，式中的界面剪切因子fi计算值对临界气速的预测至关重要；但是目前的实验手段并不能直接测出τi的大小，fi的作用机理仍然是一个未完全解决的问题，目前似乎还没有一种普适性的fi经验关系式。本文模型中的fi采用Alsaadi[21]提出的关系式(11)。

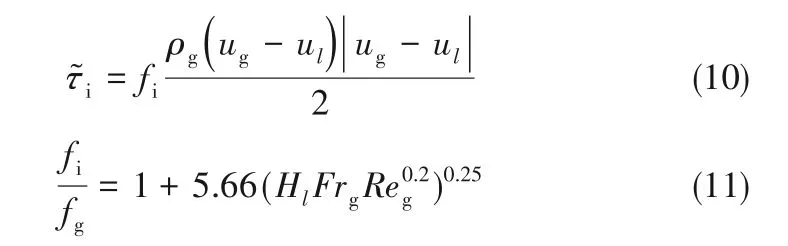
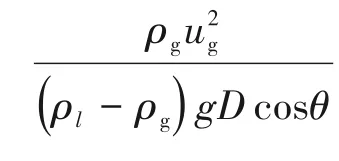
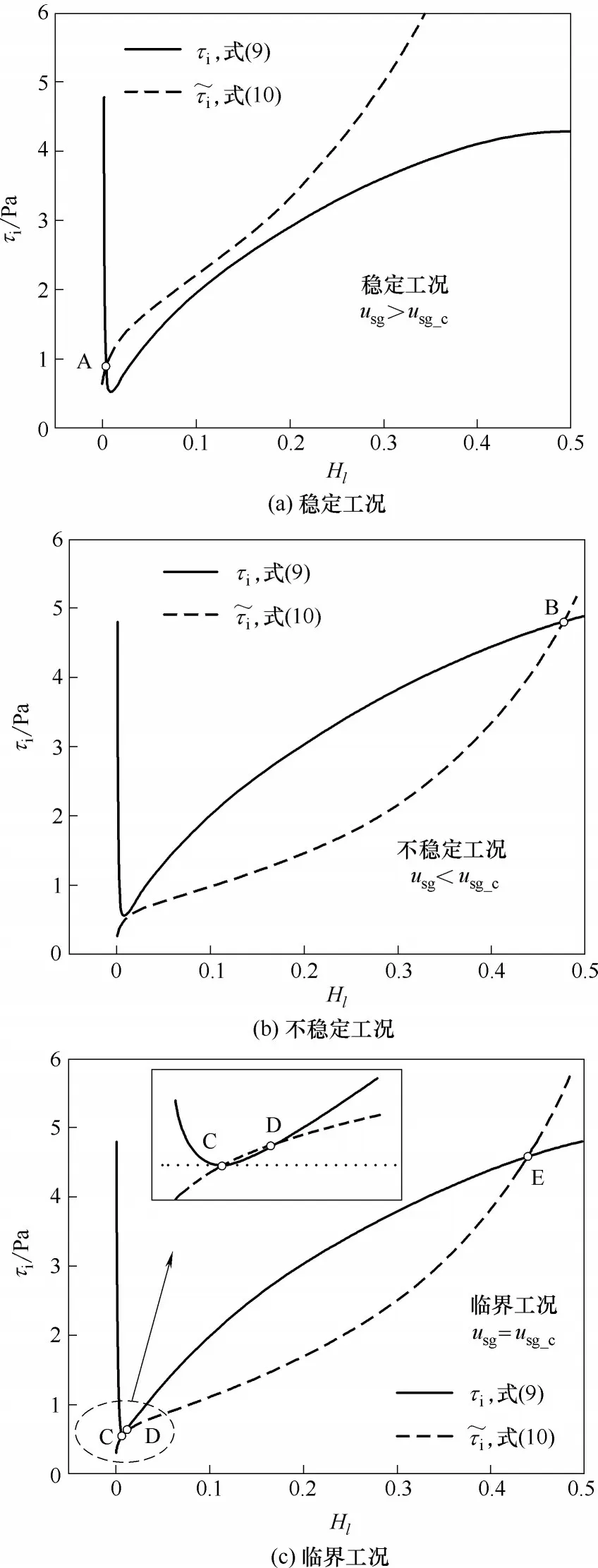
图6 与τi的交点Fig.6 Intersection of τi from Eq.(9)and from Eq.(10))。

2.4 临界气速预测

3 模型评估

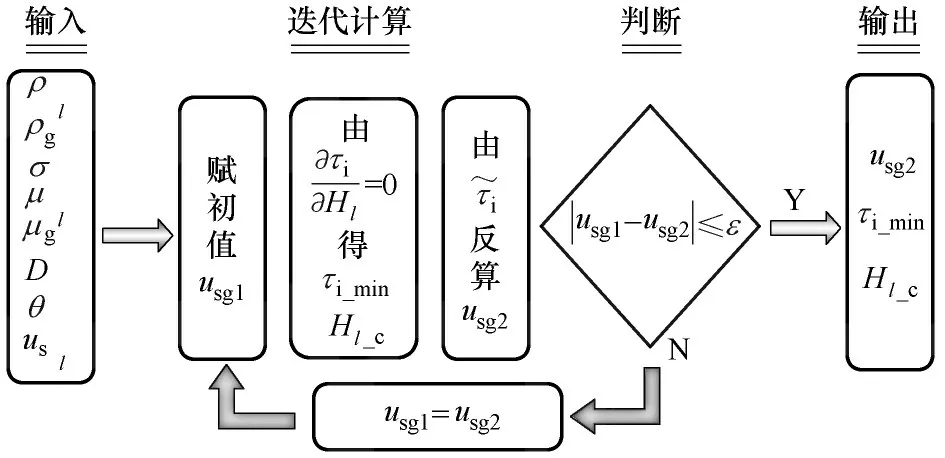
图7 临界气速计算流程Fig.7 Flow chart for calculating critical gas velocity

为了对新模型进行评估，本文收集了现有文献中可以获得的88 组实验数据用于评估模型。数据来源于表2 中的文献，其中Alsaadi[21]和Rodrigues[33]提供了分层流向假段塞流转变的数据，其余文献给出了临界气速的实验数据。但是各研究者对于临界气速的识别方法有所不同。Langsholt 等[15]将持液率突变对应的气速作为临界气速；Brito[27]、Fan[17]、Nair[34]、Alsaadi等[9]将液膜回流对应的气速作为临界气速。上述几位研究者对液膜回流的检测方法又有所不同，Brito[27]和Nair[34]往液膜中注入盐水，然后通过探针来感知液膜有无回流；Fan[17]则是往液膜注入颜料，通过注入点上游颜色变化来判断液膜有无回流；Alsaadi 等[9]仅通过高速摄像机对液膜回流进行感知，由于摄像机只能捕捉到相对宏观的现象，因此其探测液膜回流对应的气速精度可能比前两种方法低。

如图8所示，对于接近水平管道来说，不论是实验数据还是模型预测值都存在如下趋势：随着倾角和液相负荷的增加，临界气速也随之增加。

就临界气速而言，新模型预测值普遍高于Alsaadi 等[9]的实验值，但略微低于Fan[17]的实验值；整体而言新模型预测值更接近Fan[17]的实验结果。对此有以下解释。

（1）Alsaadi 等[9]与Fan[17]实验的管径均为3″，压力为常压，流体介质均为空气/水，当液相表观流速为0.01 m/s 时，两者的实验条件一致，但是两者的临界气速实验结果有差异。这可能是由于检测液膜回流的方法不同所致，前者仅采用高速摄像机，后者注入了颜料，前者感知力要弱于后者，故前者的临界气速实验值要小于后者的实验值。

表2 积液实验条件参数汇总Table 2 Parameters of liquid accumulation experiments

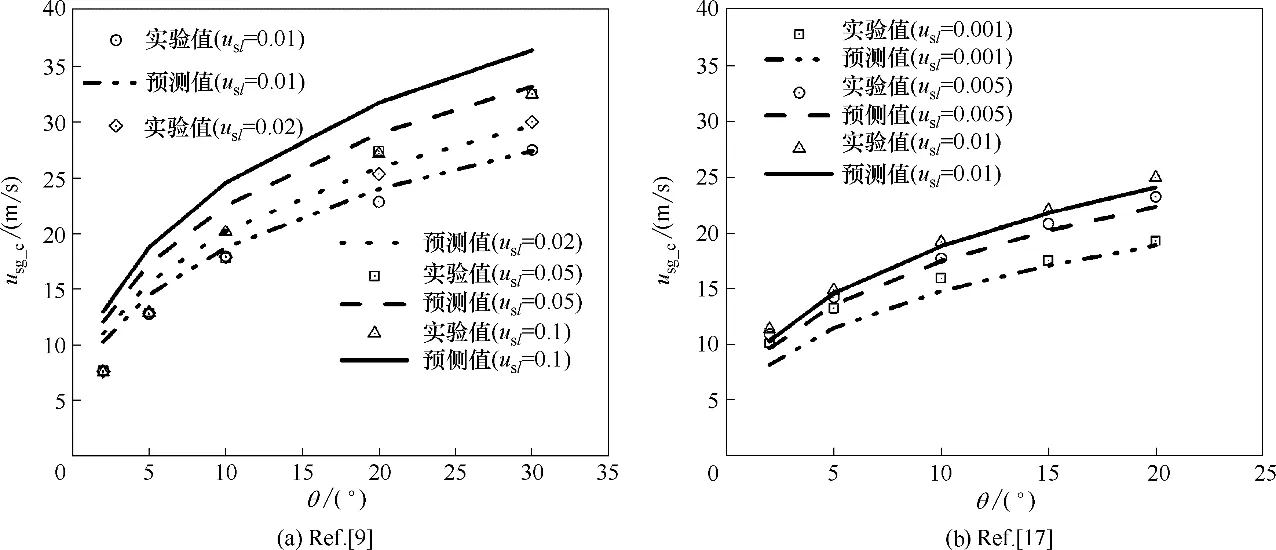
图8 新模型与文献[9,17]的实验数据对比Fig.8 Comparison of predictions from new model with experimental data Ref.[9,17]studies

（2）界面摩擦因子对于临界气速的预测至关重要，但目前没有一种界面摩擦因子的经验关系式能够适用所有工况。所以模型的预测值与实验值的偏差也可能是由于界面摩擦因子的不准确所致。

图9展示了各模型预测的临界气速与来源于表2 中88 个相应实验数据点之间的偏差。其中Alsaadi[21]和Rodrigues[33]的实验临界气速取的是分层流最小气速和假段塞流最大气速的平均值。所选取的模型为各判据中最具有代表性的模型，其中新模型和Brito[27]模型均是以分层流的最小界面剪切应力为积液判据，Alsaadi[21]模型以分层流的零液壁剪切应力为积液判据，而沈伟伟[19]模型基于持液率突变准则。图9的主图表示各模型预测值与全部实验数据的偏差。整体上看，图9(b)Brito[27]模型的预测效果最差，Brito[27]模型的预测值较多位于±25%相对偏差线之外；另外3 组模型的预测值则大部分在±25%偏差线之内。图9的缩略图为各模型预测值与来源于Rodrigues[33]、Langsholt 等[15]、Espedal[14]的比较接近高压力、大管径实验值的对比；其中Langsholt 等、Espedal 用较重的SF6 代替空气，用于模拟高压力下气相。从缩略图中可明显看出只有新模型的预测值基本在±10%相对偏差线之内。

表3所示，与全部实验数据点相比，新模型预测值的平均相对偏差为5%，标准差为16%；而与接近高压力、大管径的数据对比，新模型的平均相对偏差为-1%，标准差为8%。综合来说，本文模型最优，文献[19]模型次之，文献[27]模型的预测结果与实验数据偏差最大。

表3 各模型预测偏差Table 3 Prediction deviations for new and other models

4 结 论

积液现象发生的本质是气相对液相的携带能力不足。基于最小界面剪切应力的积液判据，引入平气液界面分层流液膜区的速度场描述，建立了近水平湿气管道积液临界气速预测新模型，提出了求解临界气速的简捷算法。本研究结论如下。

（1）对于近水平管道，模型预测的临界气速随着倾角和液相负荷的增加而增加，这与实验的变化趋势一致。

图9 各模型预测的临界气速与表2中实验值的偏差Fig.9 Comparison of predicted critical gas velocities from new and other typical models with experimental data

（2）利用已有的实验测量临界气速数据，对新模型和Brito、Alsaadi、沈伟伟三种近水平管积液模型进行评估，结果显示新模型预测的临界气速与已有的实验数据最为吻合，沈伟伟的模型次之，Brito模型的预测结果与实验数据偏差最大。新模型与全部实验数据的整体平均相对偏差为5%，标准差为16%。

（3）与其中的接近高压力、大管径数据相比，新模型预测精度更加优于其他模型，此时新模型平均相对偏差为-1%，标准差为8%。

符 号 说 明

A——面积，m2

d——管内径，m

Fr——Froude数

f——摩擦因子

g——重力加速度，m/s2

Hl——持液率

hl——液膜厚度，m

p——压力，Pa

dp/dz——压降梯度，Pa/m

Ql——液相体积流量，m3/s

R——管道半径，m

Re——Reynolds数

S——湿周，m

s——标准差

ug——气相实际流速，m/s

ul——液相实际流速，m/s

usg——气相表观流速，m/s

usg_c——临界气相表观流速，m/s

usl——液相表观流速，m/s

ε——绝对偏差

θ——管道轴向与水平方向的夹角，rad

μ——动力黏度，Pa·s

ρ——密度，kg/m3

τi——界面剪切应力，Pa

τw——壁面剪切应力，Pa

φ——液面角，即气液界面周长对应的半圆心角，rad

下角标

g——气相

i——界面

l——液相

w——壁面