基于SAPF 无源控制补偿的电力弹簧控制研究

方 乐， 周建萍， 茅大钧， 张 健， 葛祥一， 叶剑桥， 周钰婷

（上海电力大学 自动化工程学院， 上海 200090）

0 引言

配电网中电力电子装置不断增加，非线性负荷的接入使电力系统产生大量的谐波和无功，同时电网不稳定使得电网电压和电流发生畸变，严重影响了电网电能质量。 有源电力滤波器（Shunt Active Power Filter，SAPF）不易受到电网阻抗的影响， 且电网频率变化对其补偿性能影响较小，因此，SAPF 已成为谐波补偿的重要设备。

2012 年，电力弹簧（Electric Spring，ES）概念被提出[1]。 ES 通过调节非关键负载的电压来实现功率缓冲，稳定了关键负载（Critical Load，CL）的电压，使得负载侧用电量主动跟随供电侧发电量变化。ES 可以将电网电压失衡对关键负载两端电压产生的波动转移到与之串联的非关键负载（Non-Critical Load，NCL）上，自适应调节发电侧与用电侧的能量平衡。 为提高CL 两端电能质量，文献 [2]，[3] 提出了鲁棒扩展复卡尔曼滤波器（Robust Extended Complex Kalman Filter，RECKF）与模型预测控制相结合（RECKF-MPC）的控制策略，该策略需要更少的电压传感器，并解决了比例积分（PI）控制器增益调整的难题，在参考跟踪误差、 功率因数失真和总谐波失真百分比方面，所提出的RECKF-MPC 控制策略优于PI 控制器。文献[4]基于实时经验模式分解的控制技术有效缓解了理想和非理想电源电压条件下的系统谐波。 该控制算法将负载电流样本的有效分量和正序电压分量用于生成所需参考， 将失真的非线性样本分解为有限数量的本征模式函数的微尺度信号，从而降低了计算复杂性。 文献[5]，[6]采用APF控制数字参考电流， 改善了并联有源电力滤波器性能， 该控制策略以整体或选择性方式进行谐波电流补偿， 能够快速地动态抑制及其与线路电压波形的干扰，但该控制策略实现较难。文献[7]提出了一种针对三相四线制并联有源电力滤波器的离散重复控制技术， 重复控制器以其对周期信号的跟踪能力而闻名，并在所有频率下均提供高增益。在稳定CL 电压方面，文献[8]提出了ES 作为一种参与工作电压和频率响应控制的综合控制策略。通过适当的设置减轻因微电网中负载波动和发电机跳闸而引起的电压和频率波动问题， 但该控制方案较为繁琐，可行性较低。 文献[9]～[11]提出了一种用于多个ES 的分布式电压控制的一致性控制方法，实现了多个ES 的控制策略。 与传统的下垂控制相比，该方案不仅没有降低电压控制精度，还维持临界负载的电压水平，但要单独对每个ES进行控制。 文献[12]，[13]利用ES 来解决微电网中分布式电源和负载变化引起的系统电压、 频率波动问题，保证微电网的正常运行。 文献[14]提出将变论域模糊PI 控制策略应用到电力弹簧中，电力弹簧的自适应调节电压的能力得到了提高，但PI参数整定较为繁琐。

本文将采用SAPF 无源控制与电力弹簧相结合，其中无源控制策略采用注入阻尼法，该方法既可以使无源控制律具有较高的动态性能，又可以使每个控制变量快速达到期望值，具有补偿谐波电流的目的。 利用PSO 算法在线优化负载侧电压偏差，实时提高负载侧电能质量，消除了因其他控制策略而产生的通信延时问题。 在仿真软件中，该策略在电流谐波与稳定关键负载电压方面都具有有效性。

1 基于SAPF 无源控制策略补偿

1.1 SAPF 一般数学模型

基于SAPF 无源控制的ES 主电路结构如图1 所示。

图1 基于无源控制补偿下的ES 控制结构Fig.1 ES control structure based on passive control compensation

式中：D 为正定对角阵；B 为反应系统内部关系的反对称矩阵；R 为与系统储能原件有关的能量耗散正定矩阵；u 为网侧输入量。

1.2 SAPF 无源性分析及其控制律推导

无源控制（PBC）是从控制系统的结构特性出发， 从能量角度寻找与被控量相关且能收敛到控制目的的能量存储函数， 使得该能量存储函数收敛到目标值。 对于m 输入系统、m 输出系统，对∀t≥0，系统无源的表达式为

由式（10）可知，调节注入阻尼r1，r2，r3，可使负载侧的电流谐波分量收敛，达到无源控制。图2 为SAPF 无源控制策略结构图。

图2 SAPF 无源控制策略结构图Fig.2 SAPF passive control strategy structure diagram

2 基于PSO 算法的电力弹簧稳压控制

2.1 引入粒子群算法

电网电压不平衡， 会对关键负载端电压造成一定的影响， 电力弹簧将关键负载的电压波动部分转移到非关键负载处， 保证了关键敏感性负载的电压稳定。 控制策略采用PSO 算法，凭借粒子群算法处理非线性问题和快速寻优特性， 将系统运行的各项偏差在线实时优化， 使关键负载的电压稳定，同时还能保证NCL 电压运行在可靠范围内，其控制结构图如图3 所示。

图3 基于改进PSO 算法的CL 电压平衡控制图Fig.3 CL voltage balance control diagram based on improved PSO algorithm

PSO 算法具有个体进化和个体间信息共享的特点，其N 维速度和位置更新为

式中： V，X 分别为粒子的速度和位置； Yik， Xpgk分别为个体最优和群体最优； ω 为惯性权重因子，取为0.5；c1，c2为1.5；rd1，rd2为0～1 的随机数。

为稳定CL 处电压，设计PSO 算法中适应度函数fitness 为动态加权平衡度函数（Dynamic Weighted Balance Function，DWBF）：F（t）=W（t）|R（t）|。 其中：W（t）为动态权重矩阵，W（t）=（α，β，χ，γ）T分别对应的平衡度函数的系数；R（t）为平衡度函数， 其各项依次为A，B，C 三相实时电压、三相参考电压差ΔUACL， ΔUBCL， ΔUCCL，PCC 点的实时频率、参考频率的差值ΔfPCC；其表达式为

2.2 非理想条件对CL 电压影响

电网在非理想条件下对CL 各相电压影响如图4 所示。

图4 CL 电压实时误差图Fig.4 Real time error diagram of CL voltage

由图4 可知， 各相电压误差在同一水平变化且变化幅度较小，0.1 s 后趋于稳定。

为使适应度函数保证CL 处电压稳定， 对平衡度函数R（t）进行动态加权，其表达式为

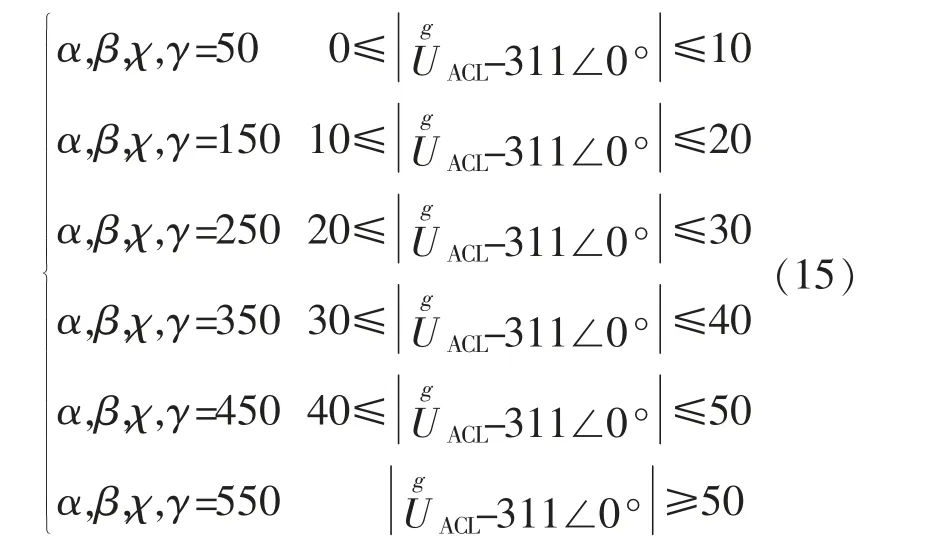
具体流程：PSO 算法模块每隔0.000 1 s 对ES所连的负载系统进行信息采集， 包括CL 各相电压、PCC 点处频率， 采样值与参考值作差形成平衡度函数R（t），同时将其输入PSO 模块。 PSO 模块作为控制中枢按照所遇工况动态设置矩阵W（t）=（α，β，χ，γ）T，然后计算出与电压不平衡度有关的适应度函数fitness， 通过算法迭代不断更新，从而协调优化CL 各相电压，使之收敛到各自的参考值，优化后的结果实时反馈到控制环中，并产生PWM 触发信号。

3 仿真实例

在Matlab/Simulink 平台下对本文提出的控制策略进行仿真验证，并与传统PI 控制策略进行对比。CL 支路分为线性负载和非线性负载两种类型， 考虑到无源控制适用于非线性负载控制，故CL 支路采取非线性负载（鼠笼式异步电机为例）；NCL 支路通常为电加热器、热水器等非敏感性负载，设为阻感性。 参数设置：电网线电压为380 V，系统频率为50 Hz， 负载侧线路阻抗为1.2 Ω，0.5 mH，NCL 线路阻抗为5 kW，3 kVar，直流母线电容为1 mF，SAPF 所连线路阻抗为40 Ω，20 mH。

3.1 基于无源控制策略的SAPF 补偿

负载侧采取非线性负载异步电机， 电网平衡时采用无源控制进行谐波补偿。 图5，6 为补偿前后的电网电流。 SAPF 补偿后电流为标准正弦波。

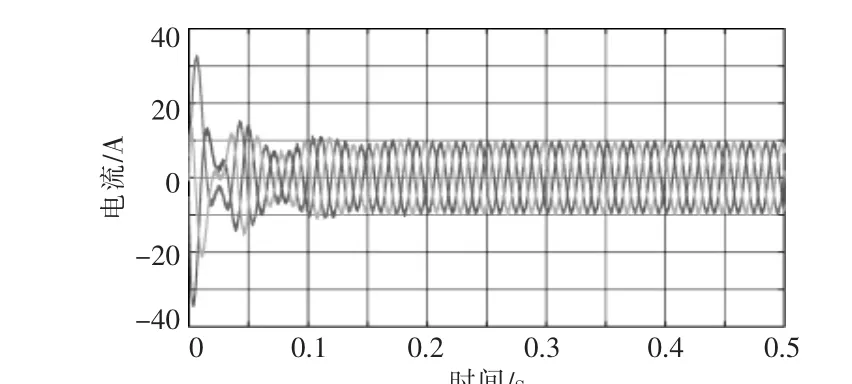
图5 SAPF 补偿前电流Fig.5 Passive control SAPF compensation

图6 SAPF 补偿电流Fig.6 SAPF compensation under passive control

图7，8 为补偿前后的电流谐波含量。 采用基于无源控制策略的SAPF 补偿后， 电网谐波含量由6.37%降到0.2%。

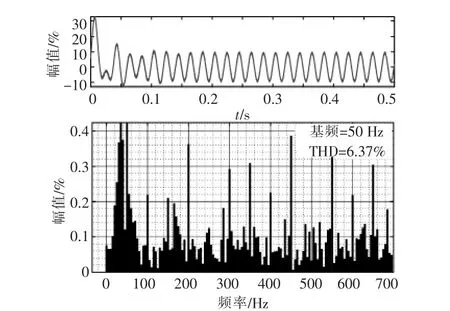
图7 补偿前负载电流谐波Fig.7 Load current harmonic before compensation

图8 补偿后电网电流谐波含量Fig.8 Grid current harmonic content after compensation

3.2 非理想工况研究

本文非理想电网工况分两种： 一是电网幅值不平衡（以A，B 两相短路）；二是电网电压相角不平衡，设置电网电压A，B，C 三相相角为-10 °，-120°，120°。 非线性负载异步电机作为关键负载，负载转矩为15 N·m，空载转速为1 500 r/min，仿真时长为0.5 s，仿真结果如图9～13 所示。

图9 幅值不平衡条件下PI 控制Fig.9 PI control under the condition of amplitude imbalance

图10 无源控制SAPF 电力弹簧稳压控制Fig.10 Passive control SAPF electric spring regulator control

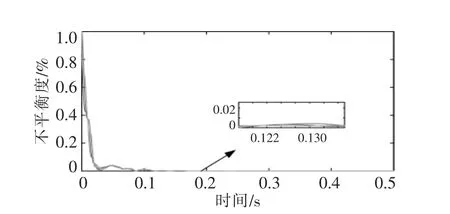
图11 改进PSO 算法的CL 电压不平衡度Fig.11 CL voltage imbalance diagram of improved PSO algorithm

图12 相角不平衡SAPF 补偿Fig.12 Phase angle unbalance SAPF compensation

图13 无源控制SAPF 补偿Fig.13 Passive control SAPF compensation

当电网电压出现幅值不平衡时， 由图9 可以看出，传统PI 控制已经不能对CL 两端电压进行有效控制， 负载侧仍出现电压不平衡现象，ES 无法实现其稳压功能。 由图10 可知，基于无源控制的SAPF 电力弹簧稳压控制，PSO 算法实时监测各相电压偏差， 并作为优化算法模块的输入量之一，在0.001 s 加入本文所提控制策略，能够有效滤除因电网电压相角不平衡而对CL 端电压造成的电压不稳定性， 使CL 各相电压快速的收敛到各自的参考值，0.1 s 后CL 各相电压分别稳定在310.6，310.8 V 和311 V。 各相电压不平衡度均低于0.01。当电网电压出现相角不平衡时，补偿前负载侧电流受到非线性负载影响， 电流幅值出现明显波动，各相相角也产生不平衡现象，补偿后的电源电流为标准正弦波。

当电网电压不平衡时，NCL 以及各线路参数均保持不变，电机负载各相关指标如图14 所示。

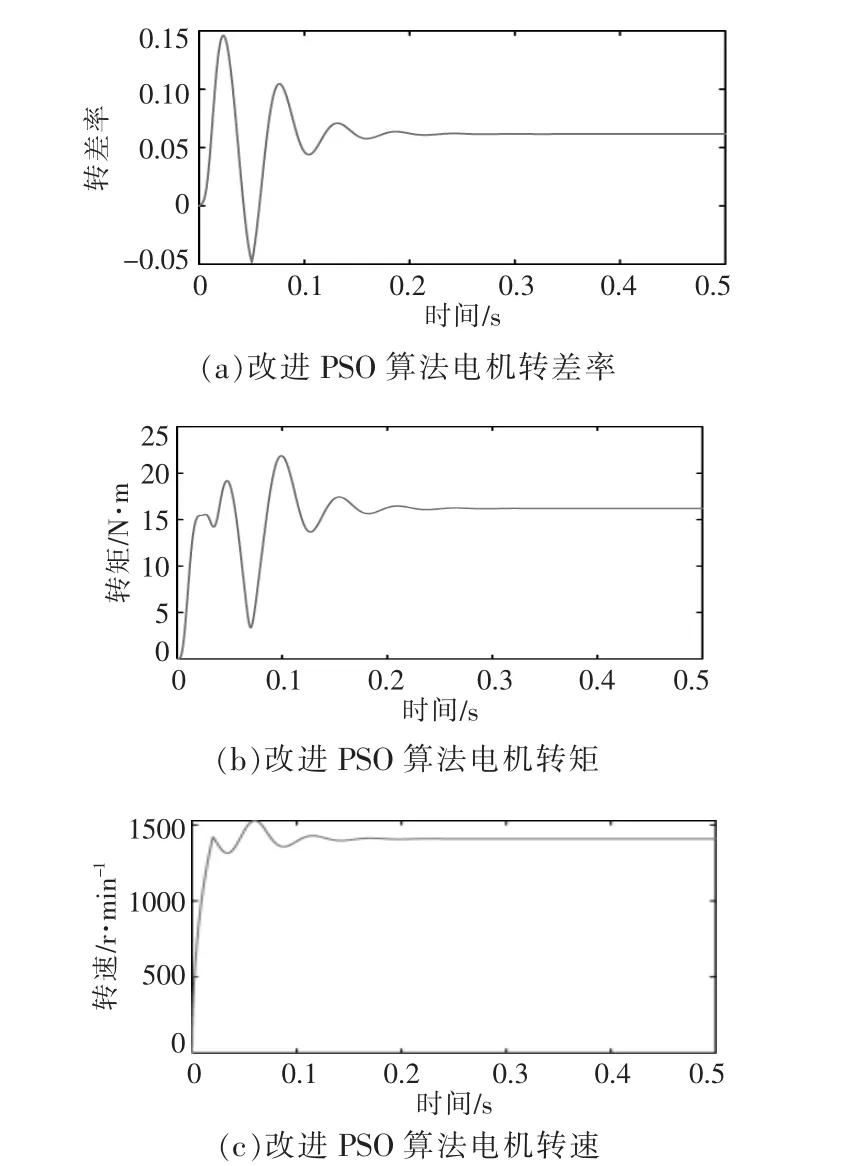
图14 改进算法后电机参数Fig.14 Motor parameters after improved algorithm

由图14 可知，电机启动0.1 s 后，电机的转速稳定在1 480 r/min， 在0.2 s 电机转矩保持在16 N·m，转差率为0.06 左右，电机正常运行。 同时基于无源控制的SAPF 电力弹簧控制可以稳定电机负载两端电压。

4 结论

本文将SAPF 无源控制策略与ES 结构相结合， 通过仿真实验得出以下结论。 ①结合SAPF系统的无源性，通过推导出的无源控制律完全解耦内环电流，注入合理的阻尼，使补充电流快速收敛到谐波参考电流，达到补充的目的。 ②与传统PI 控制方法相比， 本文无源控制方法无需处理谐波的正、负序分离环节，结构简单。③当电网出现不平衡时，可以有效补偿谐波电流。 非理想电网工况下，对于非线性负载，本文利用PSO 算法对偏差信息进行优化，保证CL 电能质量。