可再生能源双边电力市场迭代机制研究

刘 伟， 傅 磊， 刘宇明， 郭 亮

（国网山东电力交易中心有限公司， 山东 济南 250000）

0 引言

可变可再生能源（VRE）一般是指有波动特性且不可调度的能源，例如太阳能和风能。随着可再生能源发电份额的上升和成本的下降，整合VRE的成本， 尤其是与转型相关的成本收益分析计算显得尤为重要。 此外，随着电力体制改革、发电侧竞争市场的建立以及引入需求方竞争， 完全开放的双边电力市场将被建立[1]～[3]。如何建立新市场环境下的需求侧和供给侧的有效报价策略成为面临的一大问题。现阶段，对于发电量和负荷均不确定的双边市场的竞价机制研究更是甚少[2]～[4]。

为了在电力市场中容纳更多的VRE，独立的电力系统运营商（ISO）与发电厂协同工作，每个发电厂协调一套VRE 的操作。需求侧和供给侧都涉及ISO 实现的市场机制。从数学上讲，这种情况可以用最优潮流（OPF）问题的不同形式来描述[5]。在经济学中， 市场机制的研究旨在分析竞争博弈中纳什均衡的存在性和有效性， 并利用各种技术来计算纳什均衡[6]，[7]。 在电力市场背景下，文献[8]证明了电力市场非弹性需求有效纳什均衡的存在性和唯一性， 并开发了一种迭代竞价调整算法来计算市场结算价格。

本文在直流最优潮流模型的基础上， 将该模型推广到发电量和负荷均不确定的双边市场，改进了有效纳什均衡解的收敛性， 并进一步研究了该机制在不同的交易时间计划下的动态行为。 最后探讨了该机制在不同情境下的表现。

1 双边电力市场迭代机制理论基础

对于一个具有固定数量总线的电网， 在每个总线上，都有一组已知的发电/负载聚合器；每台发电机的运行发电成本由发电量的二次函数计算；每个负荷的效用由购买电量的二次函数计算。DC-OPF 问题的目标是使电力市场各参与者的经济效益最大化。在双边电力市场的竞价机制中，通常有两种类型的优化问题， 其中， 一种由ISO 解决，另一种由发电/负载聚合器解决。

优化问题在ISO 处的目标函数用数学形式表示为

式中：k 为发电/负载组数；Bk（GPk）和GPk分别为第k 个发电机的支付函数和发电功率；Ok（LPk）为负载等级LPk的负载收费。

给定发电机{bk，k=1，…，Ng}的报价和负载{ok，k=1，…，Nl}的报价与支付/收费函数的表达式是线性的，即Bk（GPk）=bk×GPk和Ok（LPk）=ok×LPk。

式（1）中的线性目标函数在所有可能的组合中最小化，并受以下约束。

①各总线j 的功率流方程

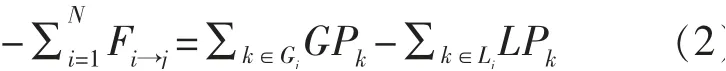
式中：Fi→j为总线i～j 的功率流 （系统中总线的总数为N）；Gj和Lj分别为总线j 上的发电机组和负载。

式（8），（9）的优化是在所有非负的GPk’s 和LPk’s 上进行的。尽管它们都取决于发电机的投标价格和负荷的报价，但式（8），（9）的GPk’s 和LPk’s的最佳组合不一定与式（1）～（5）的组合相同。 市场机制的有效纳什均衡要求两者收敛。因此，为了找到市场清算价格和相应的调度功率， 可使用如下列出的迭代算法。

1.令i=1，对于每组发电机和负载聚合器，初始化使bk（i）≥hk，ok（i）≥mk。 对于发电机，执行步骤4；对于负载聚合器，执行步骤8；对于ISO，执行步骤11。

如果在迭代结束时，发电商（负荷）的调度功率低于收益最大化时的调度功率， 则意味着其投标（报价）价格过高（过低）。 因此，在下一次迭代中，发电机（负载）需要将其投标（报价）价格降低（提高）一小部分，这与功率失配成正比。当功率失配接近0（定义了误差界）且市场清算价格收敛到均衡时，上述迭代过程可以停止。 在该算法中，价格调整的步长用δ 表示， 其值可以从0.001～0.01内选取。较高的δ 数值能够加速收敛，但也可能导致平衡点附近的波动。

2 仿真场景与数据来源

在数值仿真中，本文使用了一个改进的IEEE 9-bus 系统，该系统由6 个发电聚合器（4 个太阳能和2 个常规类型）和6 个负载聚合器组成。为了对发电数据进行建模， 本文使用了同一地区的4个太阳能发电厂和2 台天然气涡轮发电机在30 d内间隔15 min 的数据，将在同一地区的6 条线路的实际电力消耗数据作为负载聚合器的数据。 采用所选发电机的历史买价和卖价（1 h 间隔）以及各种分配功率下的负荷估计成本/效用函数中的系数。

图1 为仿真所用的电力网。 2 台天然气涡轮发电机的发电限制直接来自于调研发电资源数据， 而4 个太阳能发电厂的发电限制以及负荷则需要根据实际来估算。 负荷和太阳能发电厂的功率分布分别如图2 和图3 所示。 图1～3 中：L1～L6为6条线路；G1～G6 为4 个太阳能发电厂和2 台天然气涡轮发电机；除3 号线为30 MW 外，各线路的潮流限值为25.5 MW。在图3 中，将2 台常规发电机的数据取为输出功率与太阳能功率之和，满足实时总负荷。 发电机和负载的真实成本根据发电机和负载聚合器的历史标价和报价来假定。

图1 改进的IEEE 9-bus 系统Fig.1 Modified IEEE 9-bus network

图2 历史数据平均每小时负荷Fig.2 Hourly profiles of loads in history data

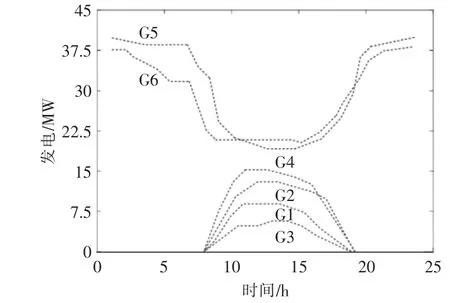
图3 历史数据平均每小时发电Fig.3 Hourly profiles of generations in history data

3 仿真计算结果

本节给出了应用于上述模拟场景的迭代市场机制的结果， 具体如下： ①为了验证本文迭代方法，将仿真扩展到具有不同水平载荷弹性的情况；②为了进一步验证模型，分别研究了VRE 条件下和不同太阳能发定价情景下的情况； ③对日前交易计划和小时前交易计划进行了比较。 通过对这些方面的研究， 本文不仅将工作扩展到具有弹性负载的双边市场， 还对不确定性和规则下的机制性能提供了见解。

3.1 荷载弹性案例

在15%，25%和50%的基础负载范围内，可以观察到灵活负载迭代机制的行为。在这些情况下，总是可以收敛。从图4 中可以看出，负荷弹性略微降低了价格。 但在图5 中，随着负荷弹性的增大，总发电量降低，对发电调度的影响显著。

图4 具有负荷弹性的发电机组在某点的均衡投标价格Fig.4 The equilibrium bid prices of generators with load elasticity

图5 具有负荷弹性的发电机组在某点的指定发电量Fig.5 The assigned generations of generators with load elasticity

3.2 具有不确定性VRE 案例

本文验证了具有不确定太阳能发电能力的迭代机制的行为。设所有发电机的下界都为零，对于太阳能电站，利用图3 所示数据的±50%均匀采样的随机数代替发电机的上界。之后，模拟运行200次。 太阳能发电机（G1，G2，G3，G4）的均衡价格统计如图6 所示。从图中可以看出，迭代机制收敛到相对稳健的纳什均衡。 即使太阳能发电能力随机变化高达50%（例如天气原因），市场结算价格也不会出现大的偏差。

图6 太阳能发电机的均衡价格频数分布图Fig.6 Distribution of equilibrium price frequency of solar generator

3.3 交易时间的影响

本文将迭代机制扩展到日前市场。 常规和太阳能发电机组的平均投标价格结果如图7 所示。虽然提前1 d 和提前1 h 之间的差异非常小，但是由于更高的负载确定性，后者应更准确。

图7 提前1 d 和提前1 h 的市场比较Fig.7 Comparison between day ahead and hour ahead markets for 24 hours

4 结论

本文研究了可变可再生能源双边电力市场迭代机制，并在改进的IEEE 9-bus 系统上进行了实验验证。 结果表明，该算法具有良好的收敛性，即使存在较大的负载弹性和较高的生存不确定性，也能达到有效的纳什均衡。此外，通过研究在不同交易时间表（日前或小时前）下的机制动态行为发现，提前1 d 和提前1 h 之间的差异非常小，由于更高的负载确定性，后者应更准确。