基于改进深度信念网络的风电场短期风速预测

王硕禾， 张嘉姗， 陈祖成， 张国驹， 郭 威

（1.石家庄铁道大学， 河北 石家庄 050043； 2.天津市市政工程设计研究院， 天津 300380； 3.天津天诚智慧能源科技有限公司， 天津 300450）

0 引言

风能是一种可再生能源。 近年来随着风力发电技术相对成熟、可靠，风能在各国能源战略中的地位不断提高。 由于滨海地区环境位置特殊，风速、温度、气压等气象因素随机性较大，对电网的安全稳定可靠运行带来了较大的影响[1]。 因此，准确地预测风速对电力系统可靠运行以及提高滨海地区分散式风电的并网能力发挥重要的作用。

当前主流的风电场风速预测方法是组合预测，将不同的模型组合在一起，使预测结果更加准确[2]。 程启明[3]提出了一种基于最小二乘支持向量机LSSVM 和集合经验模态分解EEMD 算法的组合预测方法， 得到的风速数据与实际相比较，具有较理想的效果。 都晨[4]通过模糊聚类技术处理历史数据并输入到GA 优化BP 神经网络模型中，提高了预测精度。 杨剑南[5]建立了径向基函数（Radial-Basis Function，RBF） 与BP 组合的神经网络预测模型，预测精度更高，时变特性更强。 以上的方法都可视为浅层预测模型，尽管具有很强的适应性，但不能完全提取风速数据的深层特征和内在规律。

深度学习网络是指多种类型的机器学习和各种层次结构结合在一起的网络， 使用多层非线性信息处理方法来进行识别特征、 分类数据并生成数据[6]。 文献[7]将深度信念网络（Deep Belief Network，DBN） 与k-means 聚类算法相结合，所提出的模型更加稳定，更加顺应风电的发展趋势。 本文提出了一种改进的深度信念网络（SA-ALS-DBN） 的深度神经网络风速预测模型，一方面利用模拟退火（Simulated Annealing，SA）算法优化DBN 模型初始参数，提高了提取该网络特征的效果，另一方面，利用自适应学习步长（Self-adaptive Learning Step，ALS）算法来调整DBN 训练的学习速率，解决了训练时间过长的问题， 进而准确地进行滨海地区风电场的风速预测。

1 DBN 模型

DBN 是由多个限制玻尔兹曼机（Restricted Boltzmann Machine，RBM）堆叠成的多隐含层的深度学习网络[8]。 DBN 模型是无监督和有监督的神经网络模型的组合， 无监督部分完成输入数据特征的提取，有监督部分完成分类或预测。

1.1 RBM 网络

RBM 神经网络是DBN 网络的基本组成元件。图1 为RBM 的结构。RBM 由下到上为输入可视层ν 和输出隐藏层h 组成， 层内的神经元是无连接的，但ν 和h 之间是有连接的。

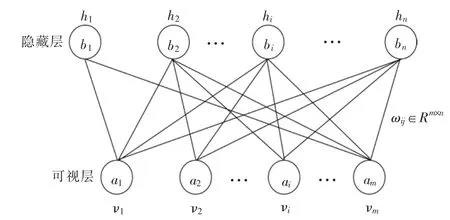
图1 RBM 结构图Fig.1 RBM structure

RBM 是一种基于能量的特殊神经网络模型，即网络模型的理想状态是能量达到最小化。 RBM对可视层到隐藏层的概率分布进行学习，其联合能量函数为

1.2 RBM 的训练

训练RBM 求解更新参数θ={ωij，ai，bj}。 为了解决计算Z（θ）用时较长的问题，采用k 步对比散度（Contrastive Divergence，CD-k） 学习算法训练RBM 参数。其主要思想是用训练数据初始化可视层，然后执行Gibbs 采样。

RBM 的训练步骤如下：

①给定训练样本集合S、训练周期J、学习率η、CD-k 算法参数k 和可视层及隐藏层的单元数目m，n；

②初始化偏置向量a，b 和不同层之间的连接权重ω；

③对样本中的ν，h 交替采样，利用P（h│ν（t-1））采样出h（t-1），利用P（ν│h（t-1））采样出ν（t），满足迭代k 次结束；

④利用下式更新参数。

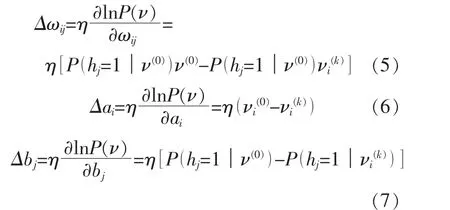
1.3 深度信念网络

DBN 的训练过程包括一个分层的预训练过程和一个微调过程，完整的DBN 的结构如图2 所示。

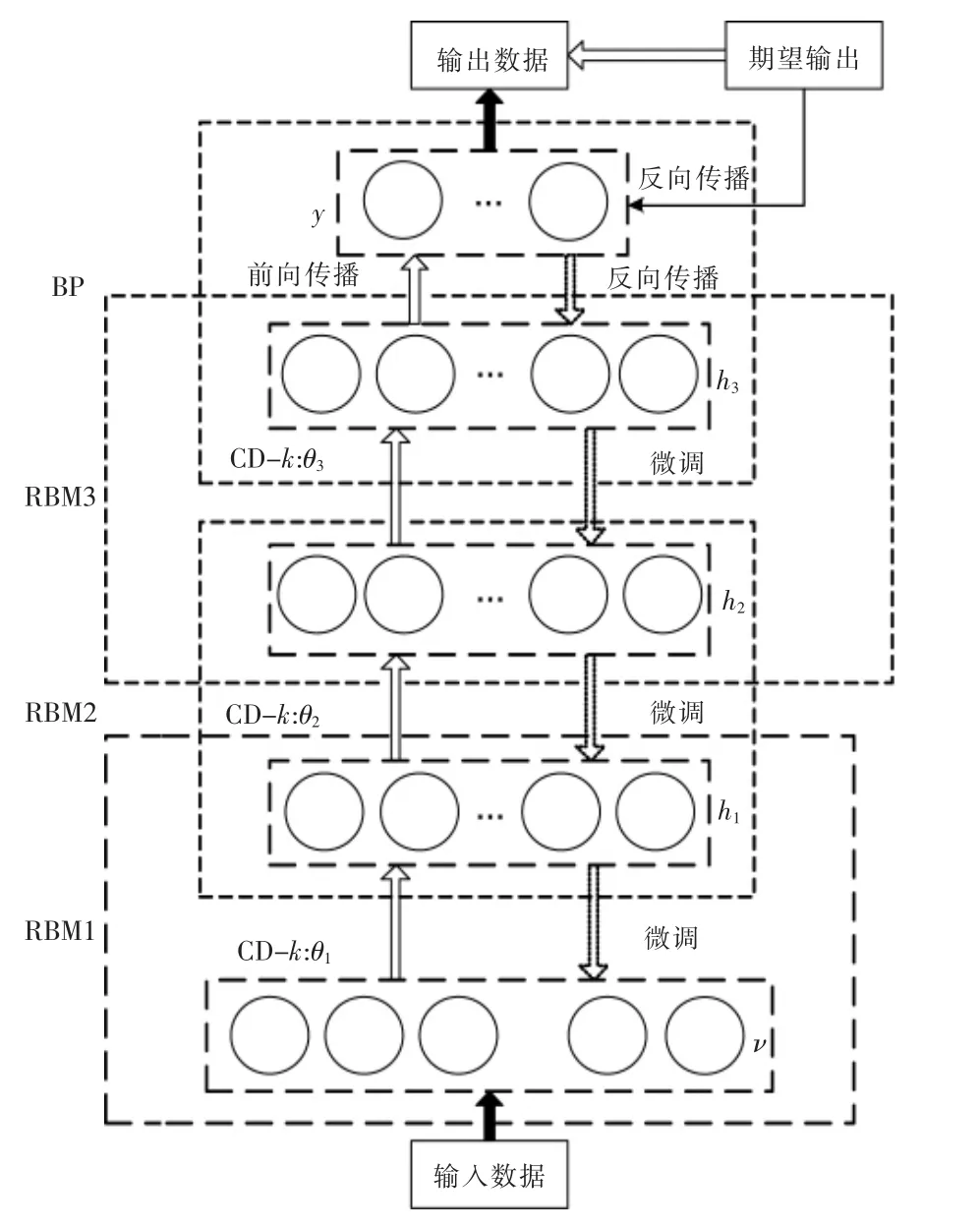
图2 DBN 结构图Fig.2 DBN structure

RBM 的具体训练步骤如下：

①分层预训练过程。 网络以无监督的方式逐层由低到高训练；

②微调过程。 网络采用BP 神经网络以有监督的方式对预训练获得的参数由高到低进行微调。

2 基于模拟退火的DBN 参数选择

滨海地区风速波动较大，导致风能特征较大。在DBN 模型分层预训练过程中，鉴于模型参数被随机初始化而导致提取的风速特征精度不高的现象，提出了利用模拟退火（SA）算法对RBM 网络参数进行寻优，解决了特征提取能力弱的问题。

2.1 SA 算法

SA 算法是一种基于Monte Carlo 迭代求解策略的随机概率寻优算法， 在一个大的搜寻空间内以一定的概率找寻命题的最优解， 克服了其他优化算法容易陷入局部极小的缺陷和对初值的依赖性[9]。

SA 算法大致分为Metropolis 准则抽样和退火两部分。

SA 算法实现步骤如下：

①给定初始温度T0，初始状态S0；

②令T=Ti，根据Metropolis 进行抽样，返回其当前状态；

③退火，令T=Ti+1；

④检查是否满足迭代次数， 满足则以当前状态输出，反之转回②。

该算法实现的流程如图3 所示。

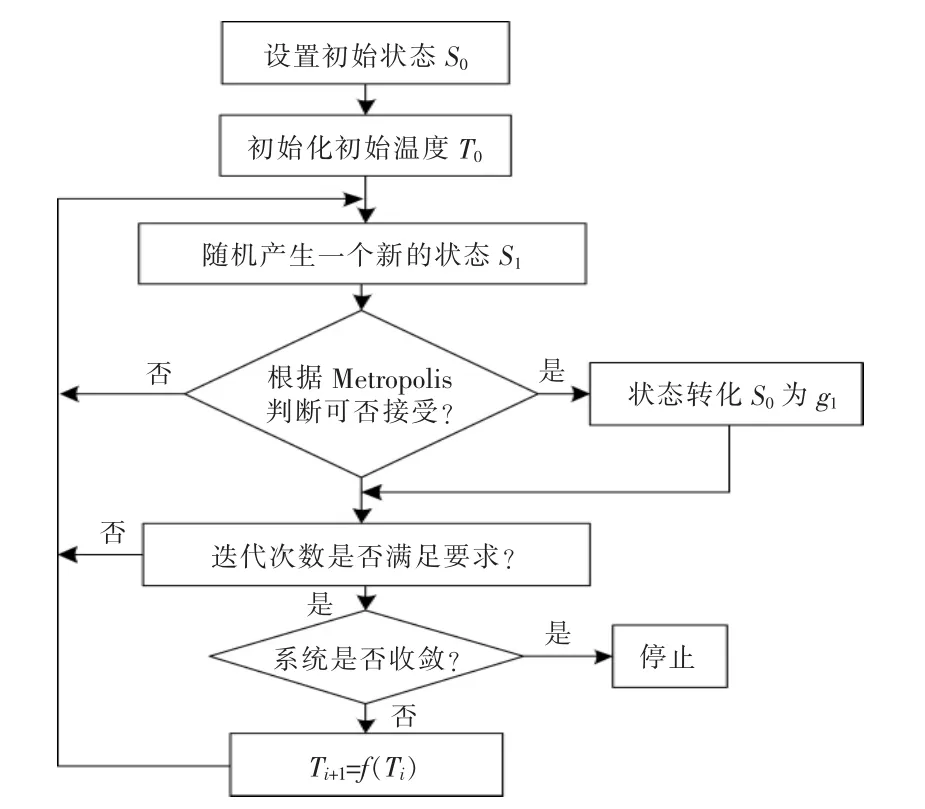
图3 SA 算法流程图Fig.3 Flow chart of SA algorithm

2.2 DBN 模型参数优化

利用SA 算法对初始DBN 参数进行寻优，目标函数是相对误差，过程如图4 所示。寻优的参数包括节点个数、训练次数和学习速率。

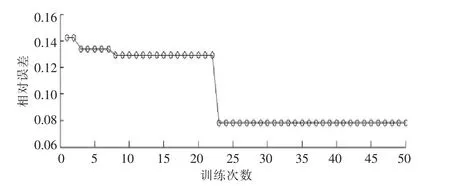
图4 模拟退火算法寻优过程Fig.4 Optimization process of SAA

由图4 可知，SA 寻优DBN 参数的过程训练了50 次，当训练次数达到23 次时，相对误差大幅度下降，降到0.077 8 后不再变化，系统达到收敛。SA 算法优化的初始DBN 参数见表1。

表1 模拟退火优化的DBN 参数Table 1 Simulated annealing optimized DBN parameters

3 自适应学习步长算法

图5 所示为学习速率对梯度下降的影响。

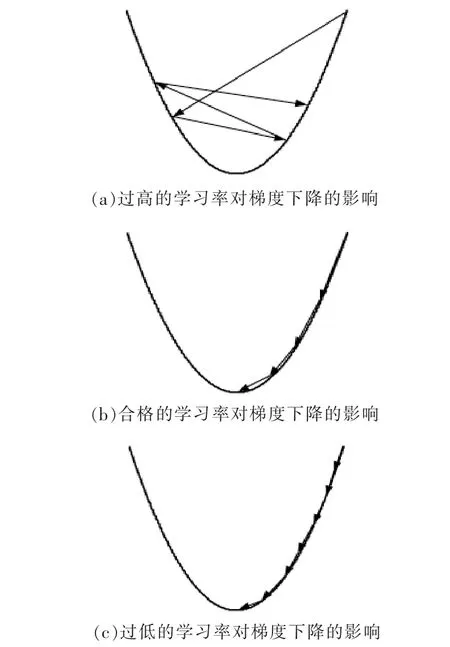
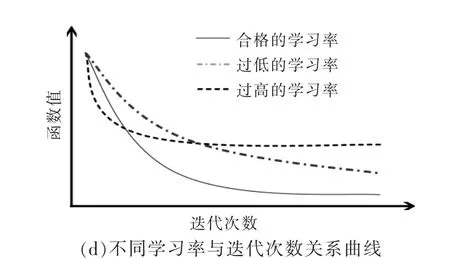
图5 不同学习率对梯度下降的影响Fig.5 Effect of different learning rates on gradient descent

由图5 可知：学习速率将会影响DBN 网络训练时的迭代次数[图5（d）]；如果学习率太大[图5（a）]， 迭代过程中很容易因为估算值可能会超出所需的最小值，从而导致不收敛；如果学习率太小[图5（c）]，一方面会因为迭代步数较多而花费时间较长，导致训练效率低下，另一方面会使序列收敛到一些局部最小值，其泛化性能很差[10]；选择正确的学习率对于训练具有良好性能的神经网络非常重要，既可以保证收敛，又可以保证效率[图5（b）]。

尽管有一些很好的指南可以手动设置学习率，但这仍然是一个非常麻烦的过程。近几年相关学者提出了几种自适应学习率方法， 例如引入自适应学习步长算法可以选择合适的学习速率，能够有效地提高训练效率和加快收敛速度。

ALS 算法将全局的学习速率η 用每个ωij，ai，bj的学习速率ηω，ηa，ηb来替换。 在k 步对比散度学习过程中，Δωij，Δai，Δbj为

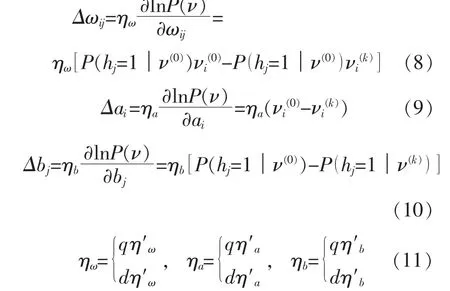
式中：q，d 分别为学习步长的增量因子、 减量因子，q＞1，d＜1。

4 改进DBN 网络的风速预测模型

滨海地区的风电场风速数据波动幅度大，对预测精度的提高有很大的影响。 本文搭建的风电短期风速预测模型基于SA-ALS 算法， 采用预处理后的数值天气预报数据与前1 时刻风电场风速数据作为模型的输入数据，风速预测值作为输出。

具体的建模步骤：①采集数据，对数据进行预处理；②利用SA 选择DBN 的始参数；③把训练集输入到DBN 模型中， 训练时利用ALS 方法自适应地调整对RBM 的学习速率； ④当目标与实际误差达到允许范围内时，结束训练，生成改进的风速预测模型， 否则返回步骤③； ⑤进行风速预测，并进行结果分析。

该预测模型的整体框架如图6 所示。

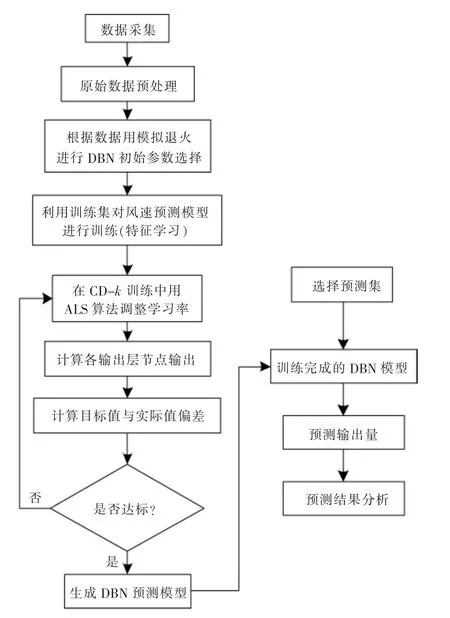
图6 改进的DBN 算法流程图Fig.6 Improved DBN algorithm flowchart

5 算例分析

5.1 数据集和数据预处理

以天津滨海地区某风电场风电机组的2017年5 月1 日-10 月31 日的数值天气预报数据与风电场历史风速数据为例进行建模分析， 数据采样时间间隔为15 min。 选取2017 年5 月1 日-10月29 日的17 472 个数据作为训练SA-ALS-DBN模型的训练集，2017 年10 月30-31 日的192 个数据作为模型的测试集进行试验， 预测未来48 h的风速。

5.2 SA-ALS-DBN 模型预测误差评价指标

本文采用平均绝对误差（MAE）与均方根误差（RMSE） 对模型的预测效果进行评价，R-平方（R2）作为衡量模型的准确性。

式中：N 为预测集的数据点数；xi为风速实际值；yi为经过SA-ALS-DBN 模型得出的风速预测值；为实际值的平均值。

5.3 SA-ALS-DBN 模型预测的实验结果

将SA-ALS-DBN 模型与其他风速预测模型进行比较， 分别采用BP 神经网络及传统的DBN网络模型进行风速预测， 并对预测结果进行误差评价。3 种模型的预测结果如图7 所示。不同预测模型对风速预测结果的MAE，RMSE 和R2值见表2。

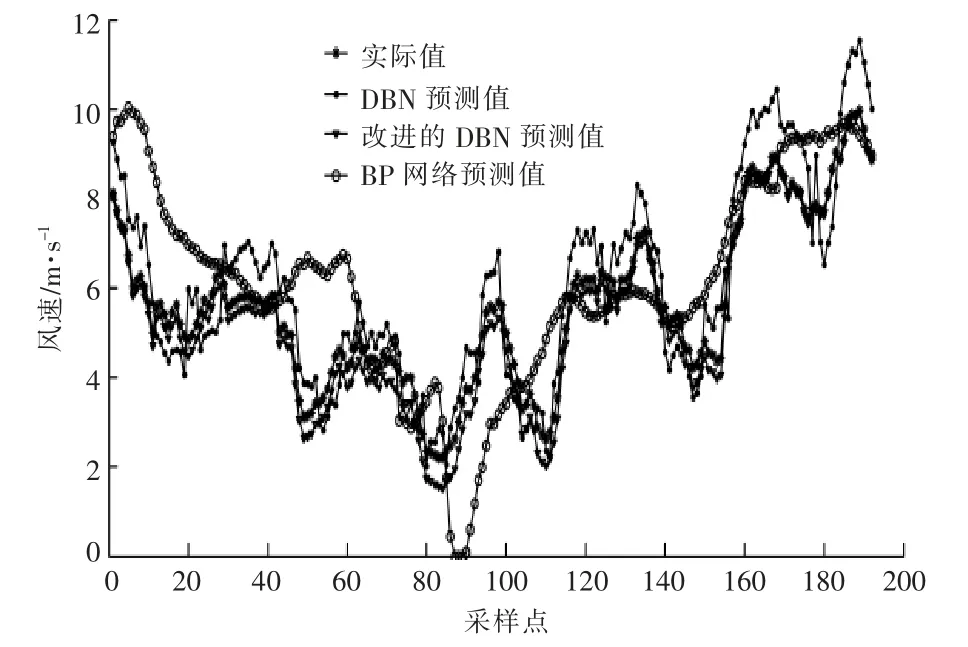
图7 3 种预测模型风速预测结果Fig.7 Three prediction models for wind speed prediction

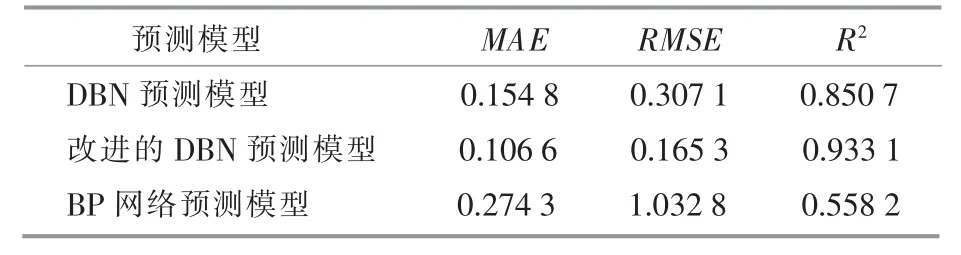
表2 误差结果比较Table 2 Comparison of error results

由图7 和表2 可知： 在误差指标方面，SAALS-DBN 拥有最小的MAE 值和RMSE 值；与DBN 网络模型的比较发现， 改进的DBN 模型的预测准确度最高，这说明改进的DBN 网络模型具有很好的特征提取能力， 更适用于滨海地区风电场的风速预测。 在利用多隐含层网络结构时，BP神经网络的训练能力弱于深度学习网络，BP 神经网络模型预测的误差及精确度相对另外两种方法较差， 说明传统的BP 神经网络方法在滨海地区不能很好的应用。

6 结论

针对滨海风电场地理位置的特殊性以及风速的随机性和不稳定性问题， 本文提出了一种新型的SA-ALS-DBN 风速预测模型。采用模拟退火算法确定了DBN 的参数，采用自适应学习步长的算法调整了DBN 的学习率，有效提高了预测精度。

经实例分析验证表明，SA-ALS-DBN 模型相比于传统DBN 模型和BP 神经网络模型，其预测效果更好。 除此之外，在与DBN 网络模型的比较中发现，改进的DBN 网络模型的预测精度显著高于另外两种方法，适应于滨海地区分散式风电场。