一种改进的压缩感知图像融合算法
汪佳瑞
(安徽师范大学物理与电子信息学院,芜湖241000)
0 引言
图像融合技术是一门集合了传感器技术、图像处理、信号处理、计算机视觉和人工智能等众多理论的现代高新技术,是将多个不同的成像传感器得到的两幅或以上的图像按照特定的规则融合成一幅图像的过程[1-2]。其中,红外图像与可见光图像融合一直是图像融合领域研究的重点与热点。红外图像是由红外传感器根据物体的热辐射差异成像的,成像过程不易受气候和环境影响,但得到的红外图像往往存在对比度和清晰度较低、细节表现不明显以及可视性较差的缺点。而可见光图像是由可见光成像传感器通过可见光的反射获取的,具有分辨率和对比度高,光谱信息丰富,可视性好等优点,但是对光照条件要求很高,在夜间、有雾或有遮挡的情况下则很难获取场景中的有效信息。基于以上两种图像的优缺点,将二者进行融合,可以实现优势互补,得到目标特征突出,背景信息丰富,视觉效果较好的融合图像,更能精确地描述出图像场景中的客观事实,有利于后续的操作和处理。因此,红外与可见光图像的融合技术可以进行目标的分类识别、军事侦察和目标跟踪等,在安防监控、军事作战等领域起到至关重要的作用[3-4]。
2006 年,Tao、Candes 和Donoho[5-7]等学者首次提出了压缩感知(Compressive Sensing,CS)理论,有别于传统的信号处理理论,信号的采样速率不再取决于信号的带宽,而是取决于信号的结构和内容。压缩感知利用信号的稀疏性,在对信号采样的同时就对其进行适宜地压缩,采样和压缩的同时进行,能在保证信息完整的情况下,使用远少于奈奎斯特采样定理[8]要求的速率来采样信息,最终获取近乎完美的重构信息。作为一种新颖的信号获取和处理理论,压缩感知不仅降低信号采样频率,明显地减少了数据的存储和传输的成本,还提高了信号处理的整体效率,避免了资源浪费的问题,为信号处理模式注入了新的思想,广泛应用于光学成像[9]、无线传感网络[10]和图像处理[11]等领域。
基于压缩感知的图像融合方法不需要知道源图像的全部采样,这无疑能减轻图像信息传输和存储的负担。但基于压缩感知的图像融合算法在压缩感知域进行测量值融合时有可能会存在一些问题,如文献[12]中对图像观测值进行融合时采用了绝对值取最大的规则,这种规则虽较为简单方便,但具有一定的偶然性和不合理性,因为随机观测下观测值系数越大,不一定就代表着信息量越大。文献[13]设计的加权融合的规则对红外和可见光图像观测值进行处理时,融合权值是根据实际的融合图像和经验进行调节,权值精确性有待提升。
基于以上原因,本文提出的红外与可见光图像融合算法在压缩感知域中进行融合时,分别采用了局部均值加权的融合规则。其原理如下:由压缩感知理论可知,通过压缩观测值重构原始图像时,是把压缩观测值的每一列看作一个整体,用来匹配获取最佳的传感矩阵原子位置[6]。因此,在对图像的压缩观测值进行加权融合时,不要破坏观测值每一列的完整性,可以将观测值的数据列当作整体进行处理,以减小重构时的额外误差。在同一种稀疏变换矩阵和测量矩阵作用下,单个压缩观测值的大小已经不能准确代表源图像灰度值的大小,以单个的观测值系数进行权值计算会影响最终的融合效果,但是测量观测值每一列的总体特性如均值、方差等却不易改变,以观测值每一列作为整体考虑,通过计算每一列的特性来衡量源图像的压缩观测值的权值,能使得融合后的观测值更加的准确和合理,从而提高图像融合效果。
1 压缩感知的基本框架
与奈奎斯特采样定理不同,压缩感知作为一种新颖的信号获取和处理理论,其理论框架主要分为三个部分:信号的稀疏表示、测量矩阵的构造和设计重构算法。
数学模型表述为:对于一个长度为N的实信号x∈RN,若信号x中只存在少量的非零分量,则表明x本身是稀疏信号。若信号x本身非稀疏,可给定一个长度为N的标准正交基,使信号x在Ψ 上是稀疏的,信号x可以表示为:
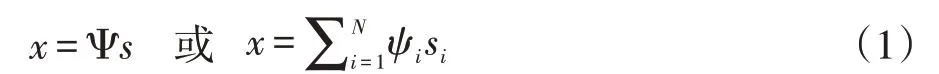
其中,s为信号x在Ψ 域的稀疏系数,当s中非零元素个数为K,且满足K≪N时,则可称信号x在稀疏基Ψ 下为K-稀疏的。在压缩感知理论中,待测信号的稀疏性是该信号能进行压缩感知的前提,也影响着信号的最终重构效果。目前常用的稀疏表示方法为正交变换法,主要包括傅里叶变换、离散余弦变换、小波变换[14]等,其中小波变换法因具有良好的时频特性,能够克服块效应,对于图像信号还能有效表示信号中各向同性点状结构,表现出了很好的逼近特性,因此常被用作图像的稀疏表示中。
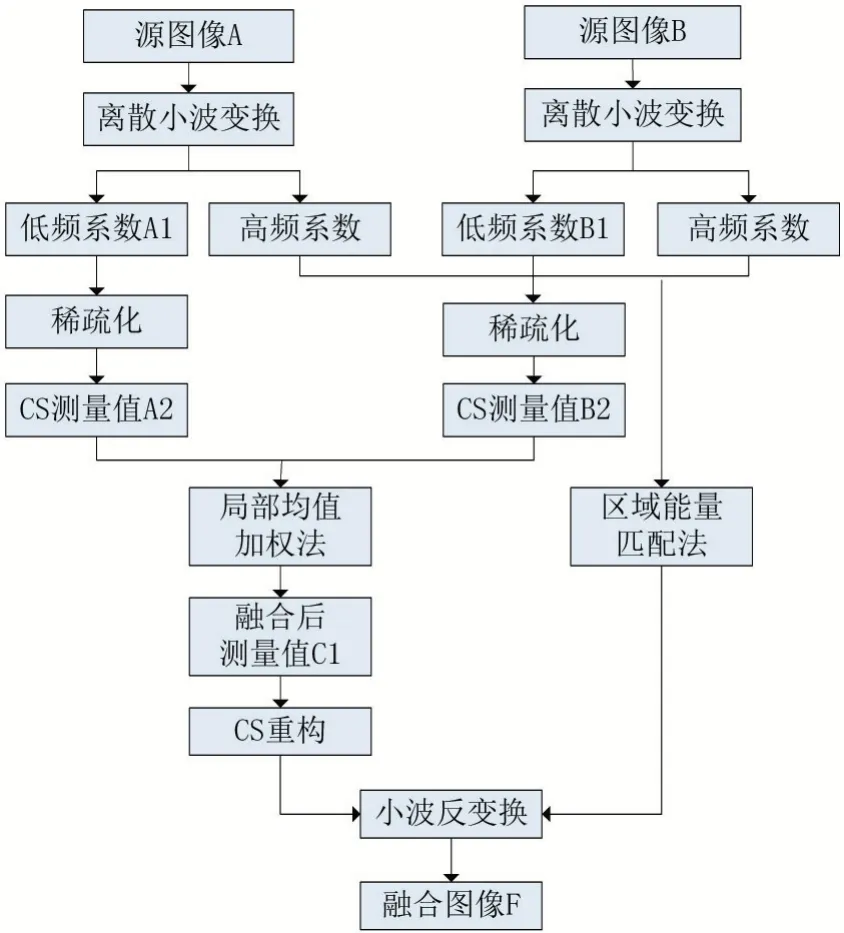
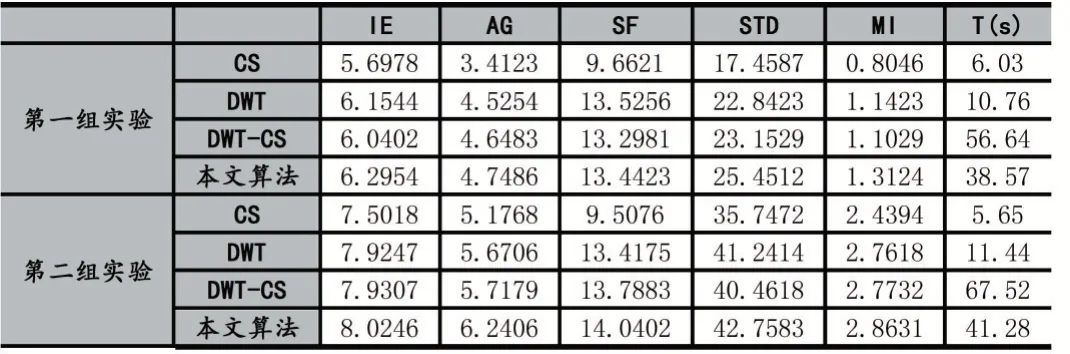
测量矩阵又可称为观测矩阵,在CS 理论中,将测量矩阵与原始信号相乘,能够实现信号的降维。具体表示为采用与Ψ 不具有相关性的观测矩阵Φ(M×N,M< 测量值y是一个M维向量,式(2)实现了测量对象N→M的降维。根据式(1),式(2)可以变换为: 其中A∈RM×N称为感知矩阵。测量矩阵需满足RIP 条件或与稀疏表示矩阵之间不相关,这是设计有效的测量矩阵的前提。目前应用较多的测量矩阵有高斯随机矩阵[5-6]、伯努利随机矩阵、多项式矩阵等,其中文献[6]已经证明了高斯随机矩阵与大多数的稀疏基不相关,同时其还具有重构过程所需的观测数量少,重构效果较好的优点而被广泛采用 信号的重构是实现压缩感知的最后一个步骤,是指从数据量远远小于原始信号的观测值y中正确地恢复原始信号。这是一个求解欠定方程组的问题,最直接方法是通过l0范数求解最优化问题来解决: l0范数指的是向量中非0 元素的个数,因此式(4)的计算结果就表示信号x在正交基Ψ 下的最稀疏解。但上式的求解是个NP-Hard 问题,在计算上很难实现。后来有研究者发现l1最小范数下在一定条件下和l0最小范数是等价的,可得到相同的解。那么式(4)就可以转换为求解l1最小范数下的最优化问题: 这也是凸优化算法的计算原理。除此之外,还可以使用贪婪追踪算法来重构信号,正交匹配追踪算法(Orthogonal MP,OMP)[15]就是一种典型的贪婪算法。在压缩感知信号重构算法中,贪婪追踪算法的计算复杂度较低、计算速度较快且重构效果较好。其基本思想是先将选用的原子先进行了正交化处理,在通过迭代从过完备原子库中选择与信号最匹配的原子来达到稀疏逼近,这种方式使得同一原子在迭代时不会被重复选择,从而减少了算法迭代次数,加快了算法收敛速度。 对于图像融合,小波变换优点表现为:将图像进行小波分解,会将其分解成低频信息和高频信息,二者包含了源图像的不同特征,可以依据它们的特征灵活地选用不同的融合规则来提升融合效果;小波变换的分解和重构过程都是非冗余的,既不会产生多余信息,也不会造成信息的丢失,整个过程中数据总量保持不变;小波分解具有方向性和多分辨率的特点,更符合人眼的视觉特性。 在本节中,我们将压缩感知理论和小波变换相结合,提出了一种基于小波变换的压缩感知图像融合算法。基于小波变换的压缩感知图像融合流程如图1 所示。具体步骤为: (1)将两幅预处理过的源图像A、B进行2 层小波分解,获得分解后的低频系数A1、B1 和三个方向上的多个高频系数。 (2)对低频系数A1、B1 进行稀疏化,然后分别通过同一观测矩阵进行观测,得到压缩域上的低频系数观测图像A2 和B2。 (3)采用基于局部均值加权的方法对低频系数压缩测量值A2 和B2 进行融合处理,得到融合后的低频系数观测值C1,最后通过重构算法得到融合后的低频系数图像。 (4)采用区域能量匹配的规则来对源图像的各高频系数进行融合处理,得到融合后的高频系数图像。 (5)对融合处理后的各个小波系数进行小波逆变换,获得最终的融合后的图像F。 图像由小波变换得到的低频系数表示的是源图像的近似,包含了源图像大部分信息,通常不具有稀疏性,要先通过本节融合算法的步骤(2)中来获得相应的压缩测量值,再采用基于局部均值加权的规则对压缩测量值进行融合,得到的融合后的压缩测量值。基于局部均值加权的规则依据的是压缩感知测量值的列的完整性,可先计算出压缩测量值每一列系数的均值,以均值大小来衡量最终的权值占比。与以单个测量系数大小来衡量权值的方法相比,由该方法得到的权值更加的合理,得到的融合后的压缩测量值更能准确反映出两幅低频图像的特征。 图1 基于小波变换的压缩感知图像融合框图 具体步骤如下: (1)首先计算两幅低频图像的压缩测量值A2和B2的列数值a2和b2,即: 式(6-7)中:i=1,2,…,N,M、N为测量值的行数和列数。 (2)分别求解压缩测量值A2和B2的列权值w1和w2: 式(8)和(9)中:i=1,2,…,N。 (3)计算得到低频系数的压缩测量值进行加权融合的局部权值w1和w2之后,需要对A2和B2进行加权,得到融合压缩测量值C1,并采用OMP 算法重建出融合后的低频系数图像。融合压缩测量值C1的计算公式为: 式(10)中:m=1,2,…,M;n=1,2,…,N。 源图像的高频系数主要包含了源图像中边缘、纹理等细节信息,将高频系数进行融合能尽可能多的保留这些有用的细节信息,补充融合图像的完整性和丰富性。而传统的高频子带融合规则如绝对值取大法只考虑到了高频图像中“像素”本身,在融合时易出现细节信息丢失和增加人为“噪声”的现象。因此本章对高频系数进行融合时采用基于区域能量匹配的规则,它不仅考虑到了高频图像中单个像素,还强调了以像素点为中心的局部区域内图像的能量特性,更能体现区域内的边缘和纹理等高频特征,使得融合效果更加突出。 为了方便区分和介绍,这里把两幅源图像离散小波变换得到的各个层次各方向相对应的高频图像统称为M1和M2,融合后的高频系数图像为M3。基于区域能量匹配的融合规则的具体步骤如下: (1)首先定义区域能量,并以此计算两幅高频图像M1、M2在像素点(m,n)处的区域能量EM1(m,n) 和EM2(m,n)。若有任意图像M,对于其上任意一个像素点(m,n),其区域能量E(m,n)可表示为: 其中,L×K定义了区域的大小为3×3,W是权系数矩阵,W=1/16[121;242;121] 。 (2)然后计算两幅高频图像M1、M2的区域能量匹配度S1(m,n),大小在(0,1]之内。 (3)获得融合后的高频系数。先设置能量匹配度阈值T1,通常取0.5 ≤T1≤1,本文中T1选择为0.6。当S1(m,n)≥T1时,表明两幅图像的高频信息比较相似,可以使用加权平均法计算融合后的高频系数M3(m,n),计算方式如(13)所示: 式(13)中,ωmax(m,n)和ωmin(m,n)是权值,分别表示两幅高频图像占比的差异性,表达式为: 当S1(m,n) 为了验证提出的基于DWT 和CS 的红外与可见光图像融合算法的有效性和正确性,选用了其他三种算法与本节提出的算法进行对比分析,分别采用了两组不同的可见光与红外图像进行试验,采用的客观评价参数有信息熵IE、平均梯度AG、空间频率SF、标准差STD、互信息MI 和耗时T。这三种算法分别为:算法1—传统的基于DWT 的图像融合算法;算法2—基于CS 的图像融合算法,图像观测值融合取极大值;算法3—也是基于DWT-CS 的融合算法,但低频系数观测值采用加权融合法,高频系数采用取最大值法。四种算法的参数设置如下:算法1 中DWT 设置为2 层分解,采用“sym8”小波函数;算法2 中CS 采用小波稀疏基进行图像稀疏化,选用服从标准正态分布且常用的高斯随机矩阵进行观测,重构算法为OMP,M/N设置为0.7;本章算法和算法3 中DWT 的参数设置与算法1一致,CS 的参数设定与算法2 一致。 两组可见光与红外源图像分别如图3(a)(b)和图4(a)(b)所示,且均已完成配准,第一组源图像大小为256×256,第二组源图像大小为320×320。图2 和图3 中的(c),(d),(e),(f)分 别 为CS 算法、DWT 算 法、DWT-CS 算法和本文算法的融合结果图。 图2 第一组图像融合实验结果图 图3 第二组图像融合实验结果示意图 从视觉效果来看,第一组实验中,CS 算法的融合图像视觉效果为最差,整幅图像失真明显,充斥着大量噪声。DWT 算法得到的融合图像整体的亮度偏暗,虽然广告牌上的信息也能识别,但人物、路灯等目标表示不够显著。DWT-CS 算法的结果图像中人物、轿车和路灯等目标的表示较为显著,但广告牌信息的描述较差。本文提出的算法视觉效果最好,广告牌上的信息能明显分辨,轿车、行人和路灯等目标突出,图像细节丰富。第二组实验中,CS 算法的融合图像视觉效果也是最差的,虽然也实现了两幅图像的融合,但融合图像明显失真,除了人物轮廓比较清晰外其他事物显示模糊。基于DWT 算法的融合图像亮度偏低,人物目标不够突出,但背景区域表现清晰。基于DWT-CS 算法的融合图像中人物比DWT 算法中的更为显著,但是细节信息不够丰富,图像中草丛、门等景物纹理不清楚。经过本文算法得到的融合图像整体视觉效果较好,保留了DWT-CS 算法中目标人物显著性的同时也保留了DWT 算法较好的细节表现能力。图像中人物轮廓突出易辨,草丛、门和左上角建筑描述得较好,背景信息丰富。 表1 为两次实验中客观参数,由此可知本文算法在两次实验中所耗的时间虽然比CS 算法和DWT 算法要长,但也明显小于DWT-CS 算法的耗时。同时,信息熵IE、平均梯度AG、标准差STD 和互信息MI 的数值均要高于其他三种算法,平均比第二名分别提高了0.12、0.31、1.90 和0.13,表明基于本文算法得到的融合图像包含的信息最为丰富,细节表达能力最强。另外第一组实验中空间频率SF 要略低于DWT 算法,又高于DWT-CS 和CS 算法,说明本文算法在清晰度的方面还有待提高。因此,从客观参数的整体观察,本文提出的基于压缩感知的可见光与红外图像融合算法的融合效果是四种融合算法中最好的。 表1 不同算法融合效果的客观评价 将压缩感知算法应用于图像融合领域,并结合小波变换,提出了一种基于压缩感知的红外与可见光图像融合算法,对低频系数和高频系数分别采用不同融合规则进行融合。对低频系数先进行压缩感知测量,根据压缩感知观测值列的完整性,提出了一种局部均值加权的方式进行融合处理,对高频系数采用的是区域能量匹配的规则进行融合,最后将融合后的低、高频分量进行小波逆变换得到融合图像。仿真实验表明,文章算法与传统算法相比提高了融合质量,得到的融合图像不仅红外目标突出,其背景和细节信息也更加丰富,图像的对比度更高。同时,该算法也存在一些需要改善的地方,如融合图像的清晰度需要进一步提高,运算速率也要加快。

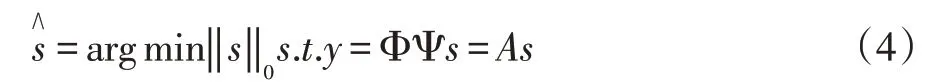
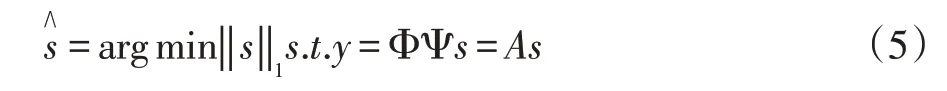
2 基于小波变换的压缩感知图像融合算法
2.1 低频系数融合规则

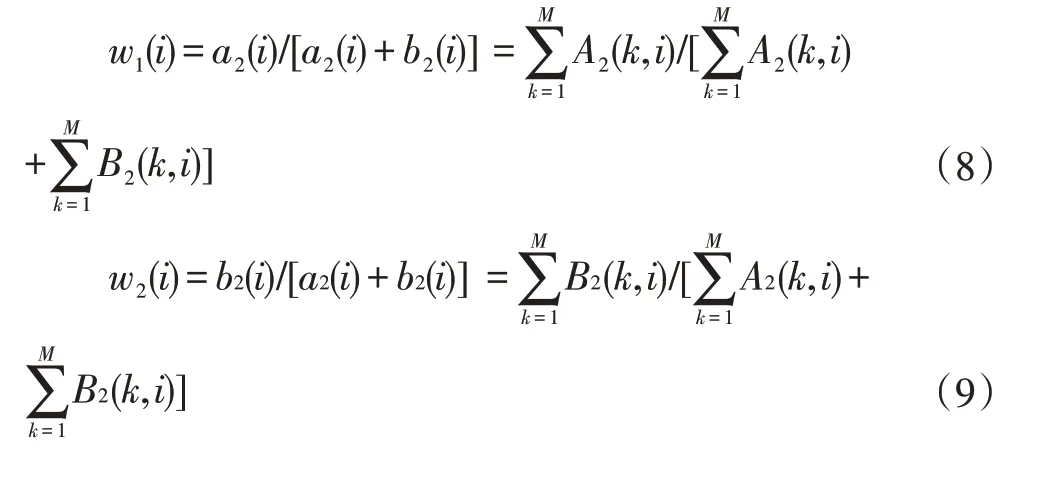
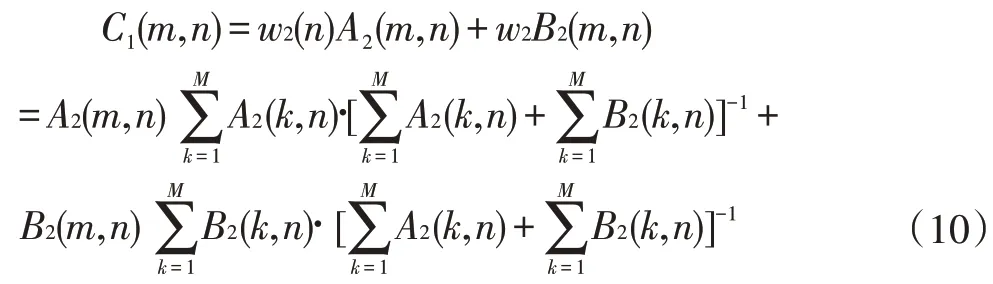
2.2 高频系数融合规则
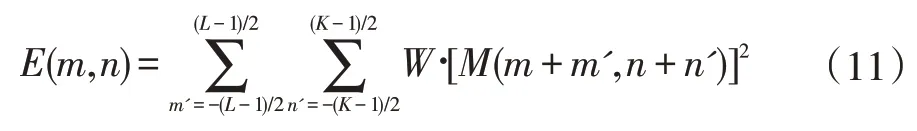
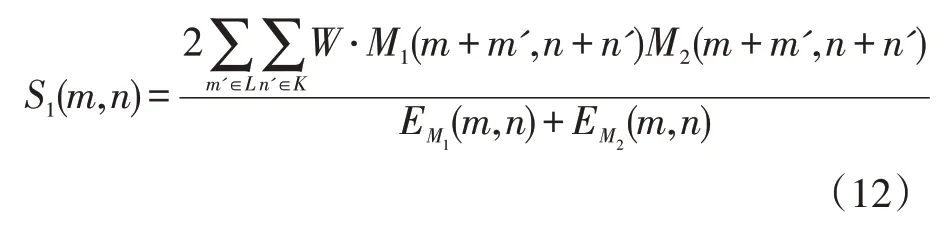

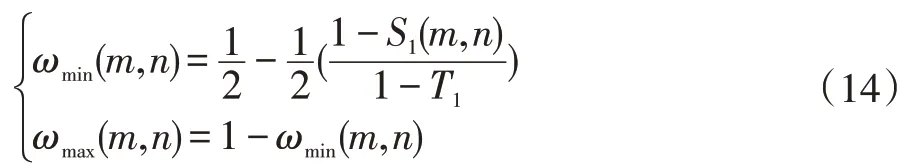
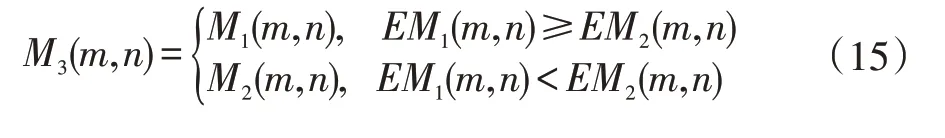
3 实验结果与分析


4 结语

