基于蚁群优化K均值聚类算法的滚轴故障预测
陈湘中,万烂军+,李泓洋,李长云
(1.湖南工业大学 计算机学院,湖南 株洲 412007;2.湖南工业大学 智能感知与网络化控制湖南省高校重点实验室,湖南 株洲 412007)
0 引 言
滚轴是机器中的易损部件,是否能够准确地诊断出其发生了何种故障及故障程度,对于滚轴的健康维护和安全运行是非常重要的,目前已经研发了多种滚轴故障诊断方法[1-5]。经验模态分解[1,2]是常用的轴承故障诊断方法之一,该方法是直观和后验的,但在使用过程中易产生过包络、欠包络以及端点效应等问题。
聚类算法是一种非监督学习方法,而K均值聚类算法[3,6,7]是最为经典的基于划分的聚类方法,采用距离作为相似性的评价依据,距离越近,则相似度就越大。孟凡磊等[3]结合局部特征尺度分解与K均值聚类分析对滚轴进行故障诊断,该方法是经验模态分解的改进,解决了过(欠)包络的问题。但K均值聚类算法通常随机选择K个初始的聚类中心来确定一个初始划分,一旦初始聚类中心选取不合理,就容易陷入局部最优解。蚁群优化(ant colony optimization,ACO)算法具有强大的全局寻优性和适应能力强等优点,该算法已广泛应用在多个研究领域[8-11]。蚁群优化算法的全局寻优性可弥补传统K均值聚类算法随机选择初始聚类中心的缺陷,从而使得聚类效果更佳。
鉴于此,在传统K均值聚类算法的基础上,提出一种基于蚁群优化K均值聚类算法的滚轴故障预测方法,针对西储大学的滚轴数据集进行测试,结果表明所提方法能有效提高滚轴故障预测的准确率和稳定性。
1 基本理论
1.1 蚁群优化算法概述
ACO算法的灵感来自对真实蚁群觅食行为的观察,蚂蚁常常可以找到食物源头与蚂蚁巢穴之间的最短距离,这是通过蚂蚁摄入食物所沉淀的称为信息素的化学物质来实现的[8]。蚂蚁利用自己对食物气味来源的知识(启发素)和对食物路径的决定(信息素)来搜索路径。蚂蚁在路径搜索过程中,通过存放自己的信息素来确定路径,这会使得信息素踪迹越来越密集,更有可能被其它蚂蚁选择。这是一种学习机制,蚂蚁根据自己对路径的认识,最佳路径将从巢穴向食物标记。
如图1所示,假设蚂蚁想从A点移动到B点,若无障碍物,它们将沿直线路径(AB)移动(图1(a))。若存在障碍物,蚂蚁将随机地转向左(ACB)或转向右(ADB)(图1(b))。由于ADB路径比ACB路径短,沉积在ADB路径上的信息素的强度大于ACB路径,故吸引了更多的蚂蚁来到此路径(图1(c))。

图1 蚂蚁寻找最短路径示例
1.2 K均值聚类算法概述
K均值聚类起源于信号处理,是最经典的聚类分析方法,K均值聚类的核心目标是将给定的样本集D={x1,x2,…,xm} 划分成k个簇,并给出每个样本对应的簇中心点[7]。该算法的步骤如下:
步骤1 数据预处理,如归一化等。

步骤3 定义代价函数,如式(1)所示
(1)
步骤4 令t=0,1,2,…为迭代次数,重复步骤5和步骤6,直到J收敛。
步骤5 对于每一个样本xi,根据式(2)将其分配到距离最近的簇
(2)
步骤6 根据式(3)重新计算每个类簇的聚类中心
(3)
K均值聚类算法在迭代时,若当前J还不是最小值,先固定簇中心 {μk},通过调整每个样本xi所在的类簇ci来让J变小;然后固定 {ci},通过调整簇中心 {μk} 使J变小。交替循环这两个过程,J单调递减:当J达到最小值时,{μk} 和 {ci} 均将收敛。
2 基于蚁群优化K均值聚类算法的故障预测方法
本文提出的滚轴故障预测方法主要由基于小波包分解的数据预处理、特征向量归一化和基于蚁群优化K均值聚类算法的故障预测模型训练这3部分组成,滚轴故障预测流程如图2所示。
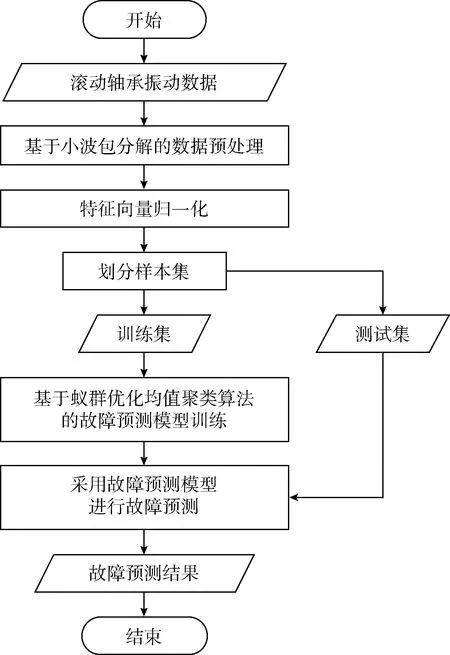
图2 滚轴故障预测流程
在滚轴故障预测中,首先对滚轴原始振动数据进行小波包分解,得到特征向量;接着对特征向量进行归一化,得到样本集;然后将样本集划分为训练集和测试集。针对训练集中的数据,采用蚁群优化K均值聚类算法进行滚轴故障预测模型的训练,得到滚轴故障预测模型;然后采用滚轴故障预测模型对测试集中的数据进行测试,根据得到故障预测结果验证故障预测模型的有效性。
2.1 基于小波包分解的数据预处理
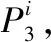
(4)
滚轴原始振动信号经小波包分解后,得到多个由8个频段能量值构成的特征向量,这些特征向量可作为K均值聚类算法的输入。
2.2 特征向量归一化
为了提高滚轴预测模型的训练速度,将滚轴振动数据经三层小波包分解后得到的特征向量按式(5)进行归一化
(5)
式中:xi(i=1,…,8) 是特征向量中第i个频段的能量值,xmax是特征向量中的最大值,xmin是特征向量中的最小值,x′i是第i个频段归一化后的结果。
2.3 故障预测模型训练
故障预测模型训练流程如图3所示,首先初始化蚂蚁数量、集群数量和信息素值;其次为每个集群随机初始化集群中心;然后根据振动数据的特征向量和聚类中心之间的距离(相似性)成反比的概率以及表示信息素水平的变量τ,将每个滚轴特征向量分配给集群。接下来,不断更新聚类中心,当迭代次数大于1000或者迭代次数大于50且收敛方案重复次数大于20的时候,终止算法得出最佳解决方案。

图3 故障预测模型训练流程
在基于蚁群优化的K均值聚类算法中,聚类工作由众多蚂蚁协同执行,对于每只蚂蚁,让每个特征向量Xn都属于一个簇。根据信息素τ和启发信息η,每只蚂蚁将每个特征向量分配给簇i的概率为P,其计算公式如式(6)所示
(6)
式中:P(i,Xn)是在簇i中选择特征向量Xn的概率,τ(i,Xn)是分配给簇i中特征向量Xn的信息素,α是控制τ(i,Xn)的影响的参数;η(i,Xn)是分配给簇i中特征向量Xn的启发信息,β是控制η(i,Xn)的影响的参数。启发信息η(i,Xn)来自式(7)
(7)
式中:Ci是簇i的聚类中心,其中d(Xn,Ci) 是滚轴特征向量Xn和聚类中心Ci的欧氏距离。通过计算每个集群中滚轴振动数据的特征向量的平均值来获取新的聚类中心,这将重复进行,并保存迭代次数a的值。再判断新的聚类中心是否收敛于旧的聚类中心,不收敛则将收敛方案重复次数b的值置为0。若收敛则在找到的m个方案中选择几率最大的解决方案作为最佳解决方案,并根据式(8)更新信息素值
τ(i,Xn)=(1-ρ)τ(i,Xn)+∑iΔτ(i,Xn)
(8)
式中:ρ是信息素挥发因子 (0<ρ≤1),这表示早期的信息素将在迭代中消失。随着更好的解决方案不断被发现,相应的信息素也不断被实时更新,其信息素对下一个解决方案具有更大影响。Δτ(i,Xn)在式(8)中是由成功的蚂蚁添加到先前信息素的信息素量,其计算公式如式(9)所示
(9)
式中:Q是一个常数,它与蚂蚁添加的信息素的数量有关;Min(k′) 是蚂蚁k′得到的每两个簇中心之间最小距离的和;Avgd(k′,i) 是蚂蚁k′得到的每个特征向量与其簇心之间距离的平均和。
3 实 验
3.1 实验数据集及实验平台
为验证本文提出的基于蚁群优化K均值聚类算法的滚轴故障预测方法的有效性,对西储大学的滚轴数据集[12]进行了测试。本实验使用了40个测试数据集,其中正常数据集4个、滚动体故障数据集12个、内圈故障数据集12个和外圈故障数据集12个。每个数据集包含10多万条滚轴振动数据,这些数据是在电机转速为每分钟1720转至1797转以及采样频率为12 kHz的工况下采集的原始振动数据。
实验平台:一台搭配了四核Intel Xeon E3-1225 v5 CPU和32 GB内存的HP Z240 SSF工作站,Win 7系统和Matlab 2014a。
3.2 振动数据特征提取
使用小波包分解对滚轴振动数据进行特征提取,每种运行状态分别得到由8个频段能量值组成的特征向量,特征提取部分数据见表1。

表1 特征提取部分数据
图4-图7是滚轴原始振动信号经小波包分解后得到的能量谱,显而易见,对于滚轴的不同运行状态,其能量分布有所不同。在滚轴正常运行状态下,其能量分布主要集中在第1频段,滚轴正常信号能量谱如图4所示。在滚轴滚动体故障下,其能量分布主要集中在第1、3、7频段,滚轴滚动体故障信号能量谱如图5所示。在滚轴内圈故障下,其能量分布主要集中在第3、7频段,在第1、2、4、8频段也有少部分能量分布,滚轴内圈故障信号能量谱如图6所示。在滚轴外圈故障下,其能量分布主要集中在第3、7频段,滚轴外圈故障信号能量谱如图7所示。

图4 滚轴正常信号能量谱

图5 滚轴滚动体故障信号能量谱

图6 滚轴内圈故障信号能量谱
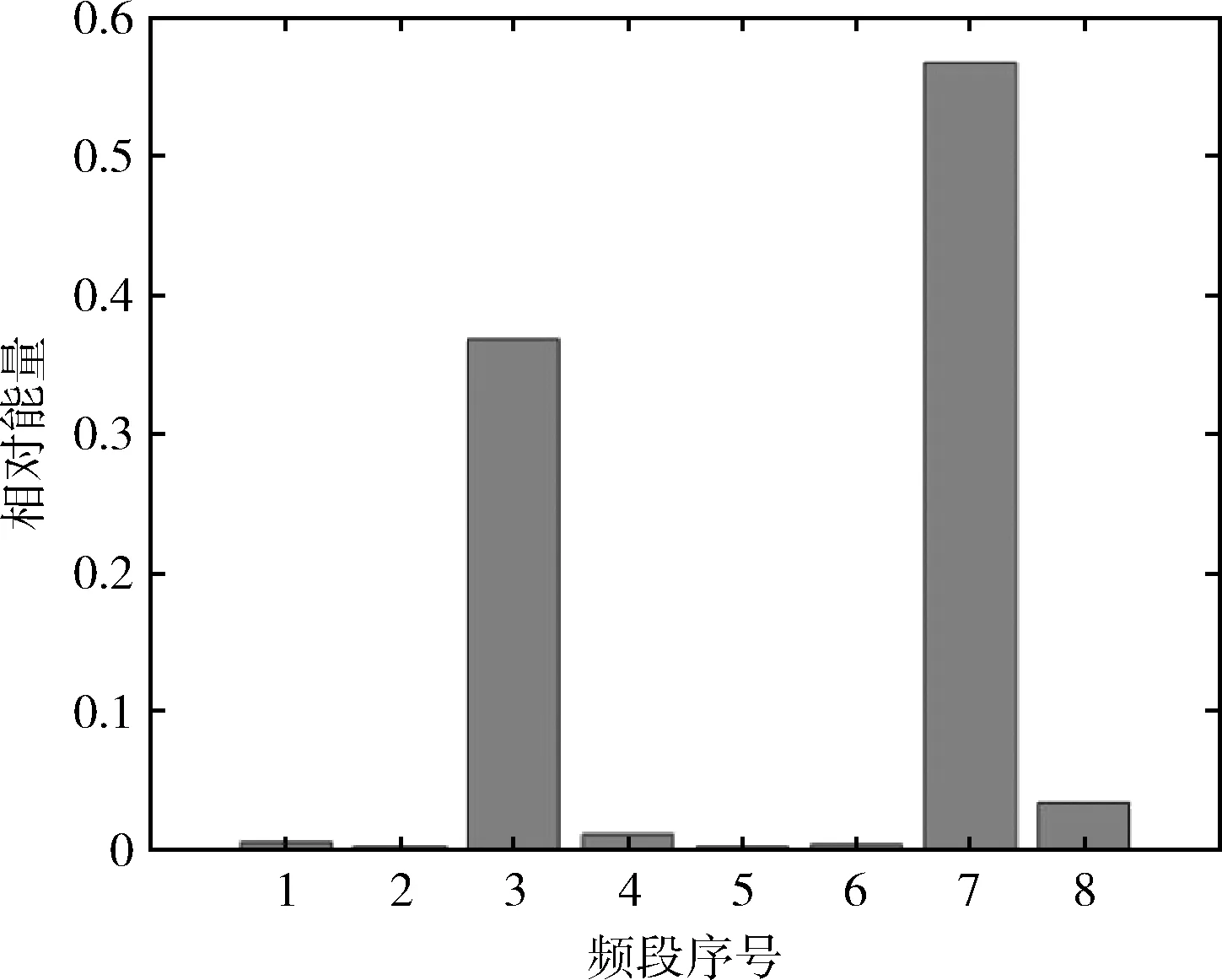
图7 滚轴外圈故障信号能量谱
3.3 实验结果分析
本实验选择了两种不同的算法:传统的K均值聚类算法(K-Means)以及蚁群优化K均值聚类算法(ACO-K-Means),使用滚轴故障预测模型对测试集进行实验,计算两种算法各自100次实验的平均故障预测准确率。实验参数设置见表2。

表2 实验参数设置
两种算法对应的滚轴故障预测准确率如图8所示,采用传统K均值聚类算法得到的故障预测准确率为91.87%,而采用ACO-K-Means得到的故障预测准确率达到了97.76%。采用传统K均值聚类算法可能得到局部优化,而采用蚁群优化K均值聚类算法更可能得到全局优化。

图8 两种算法对应的滚轴故障预测准确率
使用传统K均值聚类算法得到的4个聚类中心和它们分别对应的8个特征向量见表3,使用蚁群优化K均值聚类算法得到的4个聚类中心和它们对应的8个特征向量见表4。表3和表4中“1”是滚动轴正常运行状态的聚类中心,“2”是滚轴滚动体故障的聚类中心,“3”是滚轴内圈故障的聚类中心,“4”是滚轴外圈故障的聚类中心。与表3比较,表4的聚类中心“2、3、4”均有变化。此外,也可通过更加直观的聚类效果图来进行对比,如图9和图10所示。
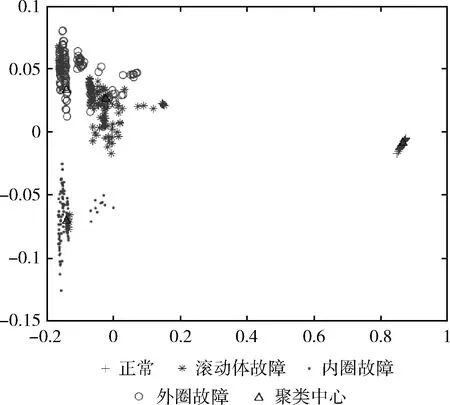
图9 使用K-Means得到的聚类效果
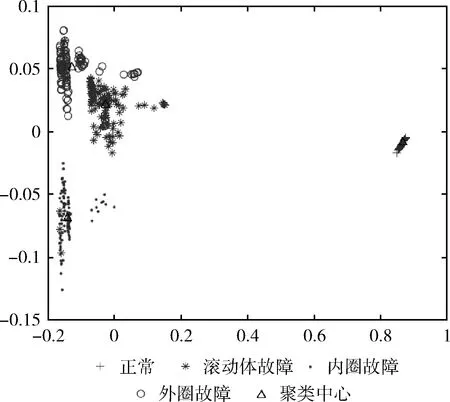
图10 使用ACO-K-Means得到的聚类效果

表3 使用K-Means得到的聚类中心对应的特征向量

表4 使用ACO-K-Means得到的聚类中心对应的特征向量
使用传统K均值聚类算法得到的聚类效果如图9所示,可以看出滚轴正常状态和内圈故障的聚类效果较明显,但滚动体故障和外圈故障的聚类效果却不是很理想,这是因为这两类故障的特征向量比较相似,聚类中心距离较近,反应出的样本整体效果很可能是局部最优,导致故障预测效果不佳。
使用本文提出的蚁群优化K均值聚类算法得到的聚类效果如图10所示,与图9相比,可以看出滚轴外圈故障和滚动体故障的聚类中心有较明显的变化,使用蚁群优化K均值聚类算法能得到更优的聚类中心,从而获得更稳定和更高的故障预测准确率。
4 结束语
本文基于蚁群优化K均值聚类算法,提出了一种滚轴故障预测方法。通过三层小波包分解得到了滚轴原始振动数据的特征向量,对特征向量进行归一化,提高了故障预测模型的训练速度。为避免陷入局部最优解,引入蚁群优化算法对传统的K均值聚类算法进行了改进,在该算法中每只蚂蚁根据先前蚂蚁留下的信息素来寻找最佳解决方案,得到了最优的初始聚类中心。在西储大学滚轴数据集上的实验结果表明,相比基于传统K均值聚类算法的滚轴故障预测,得到了更稳定和更准确的预测结果,准确率达到了97.76%。
面对实际生产中快速增长的海量滚轴振动数据,下一步将基于Spark平台对蚁群优化K均值聚类算法进行并行化,以提高故障预测效率。

