基于卷积神经网络的铁氧体零件裂缝检测

李子豪，魏东辰，严小军

(北京航天控制仪器研究所 工艺技术研究室，北京 100854)

0 引 言

铁氧体是一种常见于惯性仪表[1]中的材料，如磁悬浮陀螺轴向定子磁芯、加速度计轴向定子磁芯等零件均由铁氧体制成。在铁氧体零件的生产、加工过程中，由于各种原因，其表面可能会出现裂缝。在载体的震动颠簸下，存在裂缝逐渐加深的风险，从而导致零件失效，引起惯性仪表的卡滞，影响导航系统的正常工作。目前通过人工检测的方式在显微镜下检测铁氧体零件是否存在裂缝时，存在检测时间长、精度低等问题。在待检零件的批次较多、批量较大时，会耗费检测人员大量的时间与精力，且长时间的检测会造成检测人员眼睛疲劳，导致误检概率提高。因此，机器自动检测零件裂缝十分重要。

随着计算机算力的不断提升，卷积神经网络在图像分类、定位和检测等领域[2-6]得到了广泛的应用。深度学习的方法逐渐应用到裂缝检测领域，铁路轨道的裂缝检测[7]、建筑物混凝土的裂缝检测[8]和人行横道的裂缝检测[9]等大型物体利用卷积神经网络进行裂缝检测得到了研究人员的广泛关注，而对于小型、微型物体的裂缝检测的研究较少。且目前常见的基于卷积神经网络的裂缝检测方法[7-9]，只适用于整张图像全是待测物体的情况，不能适用于图像中包含其它区域信息的圆环形物体。

本文针对以铁氧体为材质的小型圆环形零件，开展了基于卷积神经网络的零件裂缝自动检测研究，实现了小型圆环形物体的裂缝检测，具有以下几点优势：①基于卷积神经网络，通过对图像进行四分类，实现了小型圆环形零件的裂缝检测，在验证集上达到了97%的准确率；②提出了一种滑动子区域计分方法，可有效地剔除错检区域，提升检测区域的精细程度，最小能够检测宽为0.1 mm、长度超过0.2 mm的裂缝。

图1为铁氧体裂缝检测的整体流程图，包括训练步骤、测试步骤和标注步骤。

图1 铁氧体裂缝检测流程

1 数据集制作

1.1 数据准备

选用Nikon SMZ745T显微成像系统，设置放大倍数为4倍，采集了20张分辨率为4088×3072带有裂缝区域的零件图像。去除图像中多余的背景部分，仅保留大小为3000×3000的零件最小外接矩形区域，如图1中Training下方的图所示。以步长为64像素对其进行裁剪，共得到15K张分辨率为128×128的图像组成原始数据集，有效地增加了数据集的样本数量，可以防止模型过拟合，并提高了模型对裂缝在各个位置的适应性。

将原始数据集中的图像人工分类为(a)背景区域、(b)零件边缘区域、(c)零件完好区域和(d)零件裂缝区域4个类别，如图2所示。在原始数据集中，由于属于背景区域类别的图像远远多于属于零件裂缝区域类别的图像，为了保证样本数量均衡，在各个类别中分别挑选出质量最好的2355张图像组成训练集，即训练集的图像数量为2355×4=9420。在训练的过程中，采用训练集中20%的图像作为验证集，用于检验模型是否过拟合。

图2 训练集图像的4种类别

选用不同类型的25张分辨率同样为4088×3072的铁氧体零件图像，仅保留大小为3000×3000的零件最小外接矩形区域作为原始测试集，如图1 Testing下方图片所示。具体测试方法将在第4章中进行介绍。

1.2 图像增广

为提高模型性能，解决神经网络的过拟合问题，采用镜像翻转、加入随机噪声、随机变化亮度、对比度和饱和度等方式对训练集进行图像增广。其中，加入的随机噪声为高斯噪声，它的概率密度函数服从高斯分布。

最后对图像进行标准化，将原始图像中RGB三通道的像素值从[0,255]标准化到[0,1]之间，标准化的公式为

output=(input-mi)/si

(1)

其中，mi表示第i通道的平均值，si表示第i通道的标准差(i=3)。文中的m=(0.485,0.456,0.406)，s=(0.229,0.224,0.225)。该步骤的目的是消除奇异样本数据导致的不良影响，提高分类精度并加速神经网络的收敛速度。

2 裂缝检测神经网络

本章主要介绍了用于裂缝检测的深层卷积神经网络的完整框架和训练方法。

2.1 网络框架

本次研究使用了包含残差网络结构的深层卷积神经网络，以ResNet-18[10]为基础，根据实验图像尺寸、各层输出的特征图尺寸以及分类数对网络进行了修改。该神经网络主要由输入层、卷积层、池化层、激活函数和输出层组成，其中卷积层和池化层用于进行卷积运算和池化运算，dropout[11]、批量归一化层[12]、残差块，用于防止深层神经网络性能退化和过拟合的问题。

图3展示了本研究设计的网络框架。表1给出了网络每一层的结构以及输出特征图大小。网络的输入为128×128×3的图像，通过卷积层和4个残差块，到达平均池化层，将特征图尺寸变为1×1×512，最后通过全连接层和Softmax层，输出一个4×1的向量，向量中的4个元素分别对应该输入图像属于背景区域、零件边缘区域、零件完好区域和零件裂缝区域4个类别的概率大小，其中概率最大的元素即对应神经网络输出的类别。

表1 各层网络与输出

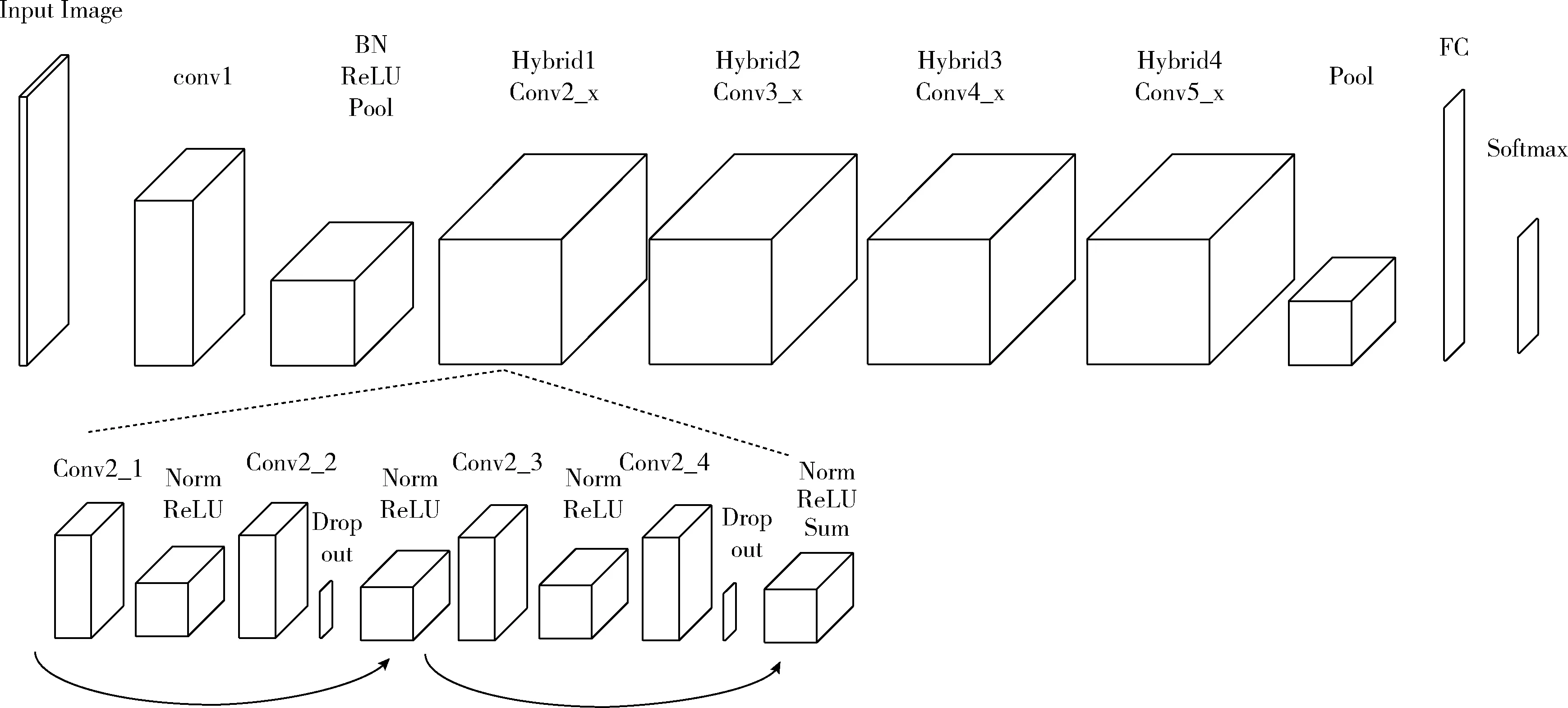
图3 卷积神经网络框架

2.1.1 卷积层

卷积层用于提取图像特征，远离输出的卷积层，对应原图像的感受野小，可以提取出细节特征；靠近输出层的卷积层，对应原图像的感受野大，反映图像的整体特征。相较于全连接层，卷积层可以保留像素点与其上下左右像素点的关系，学习到更多特征信息。卷积层局部感知和参数共享的特点大大降低了网络参数量，保证了网络的稀疏性，有效地防止了过拟合的问题。

2.1.2 池化层

池化层的作用是对特征图降采样。池化层的特征不变性使得模型更关注图像是否存在某些特征而不是特征的具体位置。池化层相当于对特征降维，特征图每个元素对应原输入数据的一个子区域，使模型可以抽取更广范围的特征。池化层还降低了输入大小，进而减小参数个数和计算量。

2.1.3 ReLU

本次研究均使用ReLU作为卷积神经网络的激活函数。ReLU的表达式为

f(x)=max(0,x)

(2)

当输入大于0，输出等于输入；当输入小于0时，输出等于0。相比于sigmoid激活函数，ReLU很好地解决了sigmoid函数在深层神经网络中出现的梯度消失问题，同时ReLU保持了sigmoid函数非线性的特点。因此，ReLU在提高神经网络性能的同时，减小了网络的训练难度。

2.1.4 Dropout

Dropout以一个设定的概率p丢弃神经元，在训练模型时可以起到正则化的作用，有效地防止模型过拟合。在本次设计的神经网络中，靠近输入层的Dropout设置p为0.1或0.2，位于网络中间的Dropout设置p为0.5。

2.1.5 Softmax

在神经网络做分类任务时，往往选择Softmax作为最后的分类层，其作用是使得所有类别得分归一化到0和1之间，正样本的结果趋近于1，负样本的结果趋近于0。神经网络输出部分的全连接层输出一个K维向量z(K为类别个数)，向量的元素代表每一个类别的得分。Softmax再将向量z“压缩”到另一个K维实向量σ中，使得每一个元素的范围在(0,1)之间且所有元素的和为1，计算公式如式(3)所示

(3)

2.1.6 残差块

由于铁氧体零件表面纹理在显微成像系统下较为复杂，导致裂缝识别难度大，并且要求裂缝检测的准确率高，需要使用较深的神经网络模型。然而，深层神经网络会出现梯度消失的问题，本次研究在网络中加入残差块解决这一问题。残差学习相比原始特征直接学习更容易：当残差为0时，堆积层仅仅做了恒等映射，网络性能不会下降；当残差不为0时，堆积层会在输入特征基础上学习到新的特征，从而拥有更好的性能。残差块结构如图4所示。

图4 残差块结构

2.2 训练方法

2.2.1 损失函数

训练采用多分类交叉熵损失函数，用来判定实际输出与期望输出的接近程度，如式(4)所示

(4)

其中，K表示类别数量，对应2.1.5节中Softmax的类别数量；yc为指示变量，如果该类别和样本的类别相同则为1，否则为0；pc为观测样本属于类别c的预测概率。全卷积层输出每个类别的得分，该得分经过Softmax层获得概率输出，模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。

2.2.2 优化算法

常用的优化算法有很多，例如随机梯度下降法、动量法[13]、RMSprop、Adam[14]等。通过对各种不同优化算法进行对比(见第3章节)，本次研究采用了Adam优化算法。Adam是一种自适应学习率的方法。它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有确定范围，使得参数比较平稳。

2.2.3 网络参数初始化

在开始训练前对神经网络参数进行初始化，采用了Xavier的方法。此初始化方法旨在使所有层中的梯度比例保持大致相同，将神经网络中的参数初始化为[-c，c]范围内的随机数，且该随机数服从高斯分布，c的计算方法如式(5)所示

(5)

其中，nin和nout分别是输入的神经元数量和输出的神经元数量。

3 实验结果评估

3.1 实验环境

本文使用的卷积神经网络在Mxnet和Pytorch框架下实现。文中出现的实验数据以Mxnet或Pytorch框架下的较好结果为准。所有的实验在Intel Core i7-5920K CPU和NVIDIA Geforce RTX 2080Ti(×2) GPU上运行。

3.2 优化算法评估

为了使损失函数更快收敛且收敛效果更好，本文分别对不同优化算法进行测试，分别选择随机梯度下降法(学习率为0.001，权重衰减5×10-4)、随机梯度下降+动量法(学习率为0.001，动量0.9，权重衰减5×10-4)、RMSProp(学习率为0.001)和Adam(学习率为0.001)作为优化算法，其损失函数收敛曲线如图5所示。由于优化算法只对训练时的损失函数起到优化的作用，因此训练时的损失函数收敛曲线可以反映算法性能。从图5中可以看出，使用Adam算法，损失函数收敛最快、收敛效果最好，在第49代时，损失函数低至0.5，且低于其它方法，因此选择性能最好的Adam算法作为优化算法。

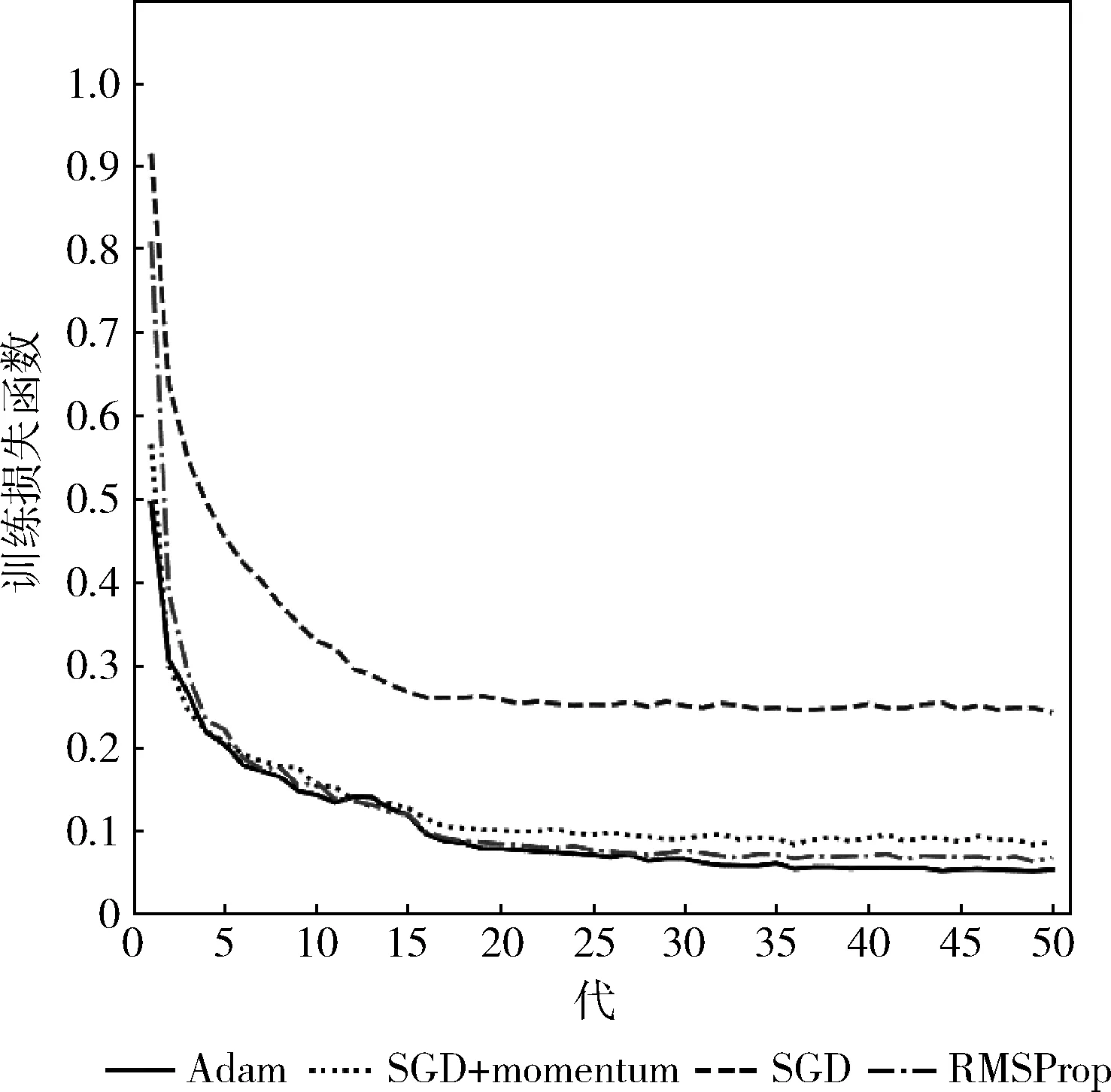
图5 不同优化算法下模型损失函数收敛曲线

3.3 神经网络性能评估

本文主要使用两个评价指标——损失函数和准确率来评估神经网络的性能。在给定的测试数据集上，正确分类的样本数与总样本数之比为准确率，如式(6)所示

(6)

按照上述数据集和训练方法对基于AlexNet[15]、VGG-16[16]、ResNet-18、ResNet-34、ResNet-50的卷积神经网络进行训练。由于验证集结果比训练集结果更能说明模型的性能，图6给出了各网络在验证集上的损失函数及准确率的对比。

从图6可以看出，相比于AlexNet和VGG-16，ResNet模型收敛更快、结果更好。ResNet模型在第5代就达到了90%以上的验证集正确率，在第50代时可以将损失函数降低到0.09以下，将验证集准确率提高到97%以上。表2给出了各网络可达到的最小损失函数值、最高准确率以及网络参数个数。可以看出，ResNet模型参数个数明显少于AlexNet和VGG-16，而性能却更优。原因主要有两个：①在相同参数的情况下，神经网络越深，训练后的神经网络性能越好，浅层神经网络的性能远远弱于深层神经网络；②ResNet在网络中使用了残差块，残差块使得深层神经网络性能更好、收敛更快。

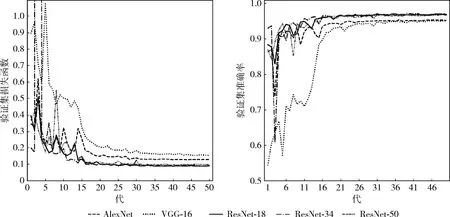
图6 不同优化器下模型准确率和损失函数

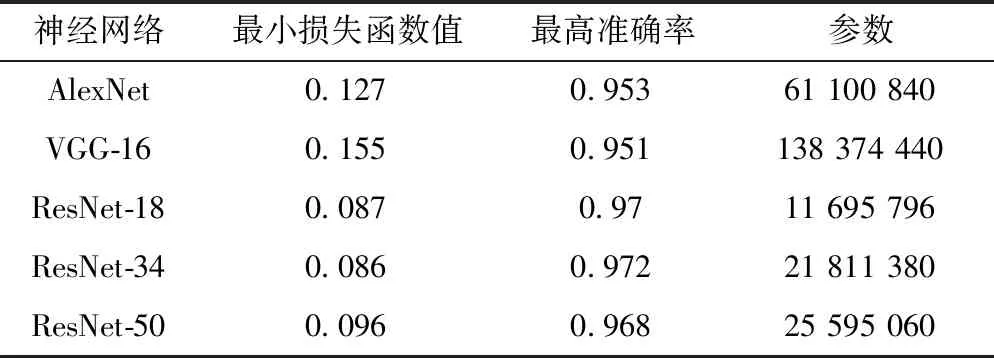
表2 各网络参数和结果对比

从图6和表2中可以看出，ResNet-18、ResNet-34和ResNet-50的性能相差不大，原因如下：在神经网络中，多次使用卷积层对图像进行特征提取，越接近输出层对应的感受野越大，远离输出的层对应的感受野越小，实验中很多长裂缝在图像中跨度很大，加入更多的卷积层才能够使得神经网络学到裂缝完整的特征信息，而图像的尺寸大小仅为128×128，更深的卷积神经网络接近输出的层的感受野重叠面积太多，学到的裂缝特征信息出现冗余，因此导致ResNet-18比AlexNet和VGG-16得到的结果更好，而ResNet-18、ResNet-32和ResNet-50得到的结果接近。

ResNet-18参数少，训练时间相对较短，批量大小设置为64的情况下，每一代训练时间大约在20 s左右，少于其它各网络训练时长。同时，ResNet-18框架在本实验中的性能相对较好，更适合裂缝检测特征提取。因此，本实验采用了基于ResNet-18的卷积神经网络，并且在该网络中加入了ReLU层、Dropout层和残差块等用于防止过拟合。图7展示了本实验设计的模型在训练集和验证集上的损失函数和准确率，模型训练集准确率最高可达到98.3%，损失函数减小至0.05；验证集准确率最高可达到97%，损失函数降低至0.087。从训练结果可以看出，训练集和验证集的准确率随着每一代稳步提升，未出现过拟合现象。

3.4 对四分类的解释

以上的裂缝检测神经网络可将目标图像分为背景区域、零件边缘区域、零件完整区域和零件裂缝区域4个类别，图7为其实验结果图。然而，在过去的一些裂缝检测研究[8,9]中，设计的卷积神经网络多采用二分类的方法寻找裂缝，神经网络模型只区分图像中有无裂缝，即背景区域、零件边缘区域和零件完好区域均属于无裂缝区域，但是类似的方法并不适用于本次研究的铁氧体零件裂缝检测。图8展示了本文设计的卷积神经网络进行二分类(将Softmax层改为2层)的损失函数及准确率。模型在训练集中可以达到90%以上的准确率；而在验证集中，准确率不到25%。

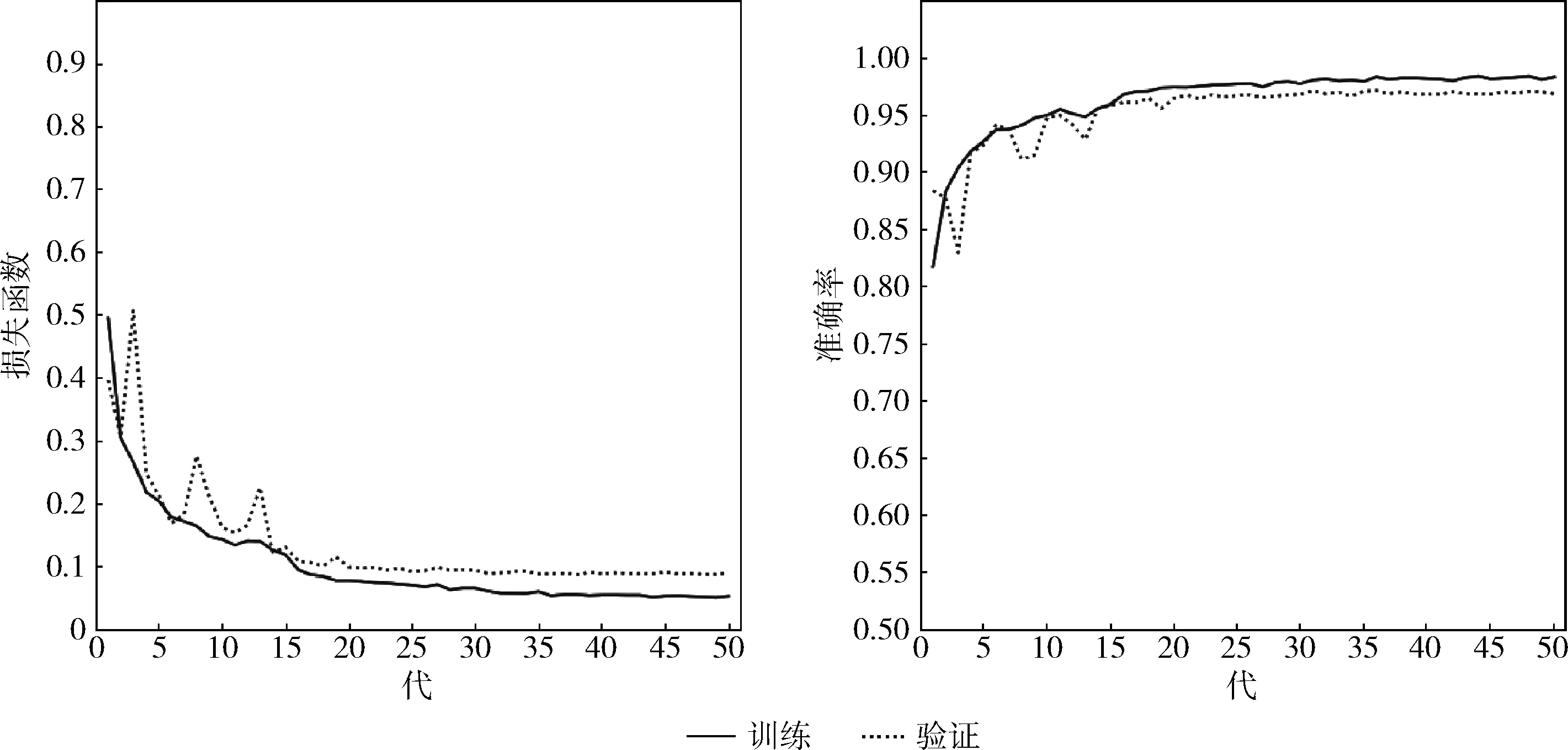
图7 实验模型在训练集和验证集的损失函数和准确率

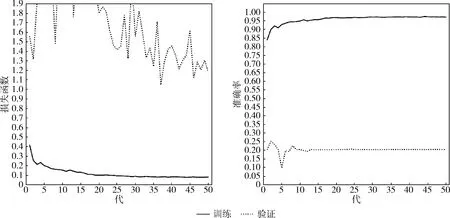
图8 铁氧体裂缝检测二分类实验

相较于图7所示的四分类实验结果，二分类神经网络并不能很好地识别裂缝特征，分析原因如下：背景区域、零件边缘区域和零件完好区域的特征相差巨大、没有显著的共同点，模型不能找到同时适应3种特征的模型参数。因此，将有无裂缝的二分类改变为背景区域、零件边缘区域、零件完好区域和零件裂缝区域的四分类可以解决二分类存在的问题，图7的实验结果验证了此结论。

4 测 试

4.1 粗检测

测试集中原始图像的分辨率是3000×3000像素，神经网络的输入是128×128像素的图像，需要以大小为128×128的采样窗口，对原始图像进行等间隔滑动采样，图9显示了当滑动步长设置为128像素时的采样示意图，此时可得到529个128×128的采样区域。

图9 步长为128像素的等间隔滑动采样

对采样区域分别进行标准化后，依次将其作为神经网络的输入，神经网络的输出即为该采样区域所属的类别。将每个采样结果的类别标注在原图中，如图10(a)、图10(b)所示，其中深灰色区域表示背景区域，浅灰色区域表示零件边缘区域，白色区域表示零件完整区域，黑色区域表示零件裂缝区域。图10(a)、图10(b)各有14和16个区域检测错误。测试集的零件和训练集的零件有明显区别，但仍有97%以上的分类结果是正确的，说明本次设计的神经网络对铁氧体零件各类型区域的分类性能好、泛化能力强。

图10 粗检测结果

4.2 滑动子区域计分

虽然粗检测可以达到较高的分类准确率，但由图10可以看出，粗检测得出的结果中错检区域较多，且检测出的裂缝区域的精细程度不高。本文提出了一种滑动子区域计分方法，可以使检测出的裂缝更加精确，同时剔除错误检测。首先将滑动步长由128像素减小为128/2N像素，其中N为缩小倍数，取值为[1,7]，本文以N=2为例，即滑动步长为32像素，采样如图11所示。

图11 步长为32像素的等间隔滑动采样

每一个128×128的采样区域可以看作是16个32×32的子区域，采用如下方式对子区域进行计分：

(1)若采样区域被分类为零件裂缝区域，给予它的所有子区域一个较大的信心分数；

(2)若采样区域被分类为零件完好区域或背景区域，给予它的所有子区域一个惩罚分数；

(3)为了保证当裂缝出现在零件边缘部分时仍能将其检测为裂缝(裂缝出现在零件边缘区域时，神经网络往往将这种情况判断为零件的边缘)，被检测为零件边缘区域的采样区域给予它的所有子区域一个较小的信心分数。

由于采样区域之间相互重叠，大部分子区域会得到多次赋值，子区域的最终分数p如式(7)所示

p=Oc+Pe-Qn

(7)

其中，O代表零件裂缝区域的信心分数，c代表该子区域被检测为零件裂缝区域的次数；P代表零件边缘区域的信心分数，e代表被检测为零件边缘区域的次数；Q代表零件完好区域和背景区域的惩罚分数，n代表被检测为这些区域的次数。设定一个阈值Tp，若子区域的最终分数p大于等于Tp，则认为该子区域是裂缝区域。

经过多次实验，在滑动步长为32像素的情况下，建议设定裂缝的信心分数O为1，边缘的信心分数P为0.5，其它区域的惩罚分数Q为2，阈值Tp为5。以该组参数，采用滑动子区域计分方法得出的裂缝检测结果如图12所示，经计算，该方法可将宽度在0.1 mm左右、长度在0.2 mm以上的裂缝检测出来。

图12 滑动子区域计分结果

此外，还可以将缩小倍数N设置为更大的值，从而将原采样区域分割为更精细的子区域，使用类似的计分方式，能够得到更精确的裂缝检测结果。

4.3 结果评估

本文使用了3种评估系数精确率Pr、召回率Re和F1分数，来测试裂缝检测方法在测试图像中的性能，式(8)、式(9)、式(10)分别是这3种评估系数的表达式

(8)

(9)

(10)

其中，TP、FP和FN分别是实际有裂缝检测为有裂缝，实际有裂缝检测为无裂缝和实际无裂缝检测为有裂缝的区域个数。对25张测试集图片进行测试。将步长为128像素(粗检测)与步长为64像素、32像素的检测结果进行对比，对比结果见表3，可以明显看出，步长为32时的精确率、召回率和F1分数更高，效果更好。

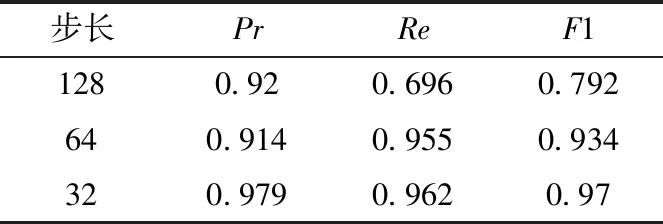
表3 不同步长的Pr、Re和F1对比

将滑动子区域计分方法的步长设置为128、64和32的裂缝检测结果对比如图13所示，其中从左到右依次是步长设置为128、64和32的裂缝检测结果图。从图中可以明显看出，在步长逐渐减小时，检测出的裂缝区域更加精细、准确，在步长为32像素时的检测结果最优。

图13 裂缝检测结果对比

在采用传统图像处理方法检测该类圆环形零件的裂缝时，无法将零件裂缝区域与零件边缘区域区分开，因此无论是精确率、召回率和F1分数，或是检测的精细程度、准确程度，都比本文提出的神经网络分类器结合滑动子区域计分的方法效果差。

5 结束语

本文针对小型圆环形铁氧体零件的裂缝检测难题，开展了一系列研究。在第一章建立了一个包含9K张大小为128×128的图像的铁氧体零件数据集。在第二章设计了一种基于卷积神经网络的裂缝检测网络，该网络可实现铁氧体零件图像的四分类。在第三章对裂缝检测网络的性能进行了评估，在验证集上的准确率可以达到97%。在第四章提出了一种滑动子区域计分方法，通过缩小滑动步长、对子区域计分、设定阈值Tp，筛选出最终分数较高的子区域作为检测结果，得出更精确的裂缝区域，并有效地剔除了错检区域，在测试集可达到97.9%的检测精度。实验数据和实验结果表明本文设计的基于卷积神经网络的铁氧体零件裂缝检测网络，结合滑动子区域计分方法，可以有效、精准地检测出铁氧体零件中宽度在0.1 mm左右、长度超过0.2 mm的裂缝，达到了小型圆环形物体裂缝检测的最优水平，具有较高的工程应用价值。