架空输电线路采用异种导线时水平相间距离影响研究

梁盼望，李 辉，杨 力，唐春林

(中国能源建设集团湖南省电力设计院有限公司，长沙 410007)

随着社会经济的飞速发展，输电线路走廊日益紧张，同塔双回、同塔多回输电线路是最常见的提高单位走廊输送能力的技术方案[1]。然而同塔双回、同塔多回线路常因回路不同期建设、回路输送容量差异，需采用异种导线，而异种导线的风摆幅值、周期差异较大，会出现导线档中水平相间距离不足的问题。

本文特针对同塔多回架空输电线路采用异种导线时的水平相间距离建模、计算等展开研究工作。

1 计算模型

本文研究以垂直排列双回220 kV输电线路为例，三相导线呈垂直“伞”型布置，塔头三相导线最小水平相间距离10.8 m，设计基准风速33 m/s，覆冰厚度0 mm，一侧回路导线拟采用2×JL/G1A-400/35钢芯铝绞线，垂直分裂间距500 mm，另一侧回路导线拟采用2×JL/G1A-300/25钢芯铝绞线，垂直分裂间距500 mm，导线悬垂串长度3 600 mm。垂直排列220 kV双回路直线塔模型见图1，图中单位为mm。

图1 垂直排列220kV双回路直线塔

2 摆动模型

输电线路导线设置在两杆塔悬挂点的线呈悬链线状态，为抽象模型，将一档导线简化为垂直悬挂的球体考虑(单摆)，导线在恒定的风荷载作用下，摆动到平衡位置，此时外力风荷载撤销后，导线呈自由阻尼摆动。悬挂在档中的导线等效为单摆后，其摆动周期如下：

(1)

式中：T为摆动周期；L为摆长，在本模型中摆长L=λ+f,λ为悬垂串长，f为弧垂；g为重力加速度，取9.806 65 m/s2。

摆动振幅公式为：

A=Lsinθ

(2)

式中：A为摆动振幅；θ为摆角。

摆角简化为导线受恒定的横向风荷载作用下的平衡位置下的角度：

θ=arctan (F/G)=arctan(W/γ)

(3)

式中：F为导线横向风荷载；G为导线垂直荷重；W为导线单位长度横向风荷载；γ为导线单位长度垂直荷重。

从上述3个公式可以看出，若同塔双回线路采用异种导线，则导线在同一横向风作用下，初始摆动幅值、摆动周期均不同，在摆动的过程中可能发生相对摆动的情况，对线路安全运行极为不利，不同档距下各线型的摆动周期见表1。

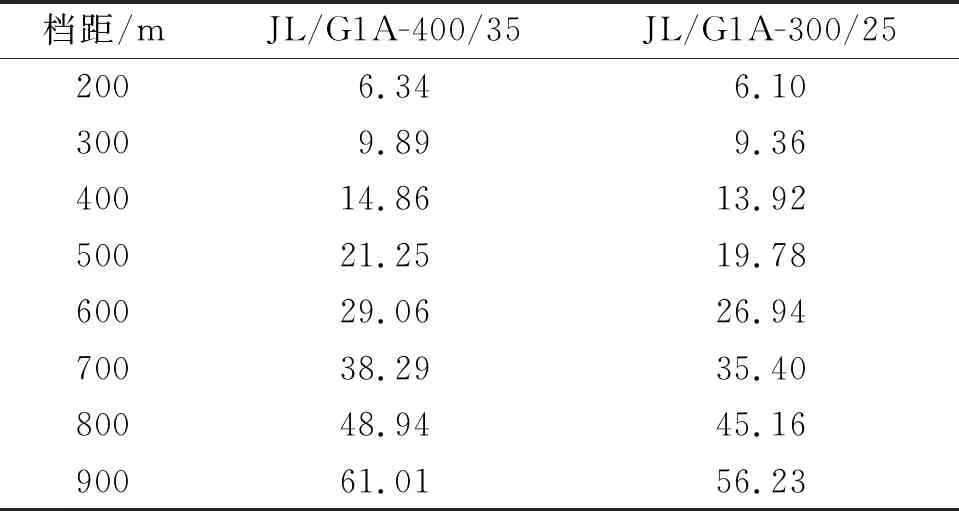
表1 不同档距下各线型的摆动周期 s

3 摆动幅值衰减模型

上述水平布置的两相导线因摆动初始振幅、摆动周期的差异，在摆动过程的某一时刻，可能出现相对摆动的情况，但摆动过程是一个阻尼衰减的过程，经过若干周期后，虽然导线相对摆动，但导线衰减反而增大了导线的水平相间距离，因此需对导线摆动振幅随摆动周期的变化趋势梳理出来，导线摆动过程遵从能量守恒定律，在摆动过程中受风阻产生能量损失，摆动幅值随之衰减。

以第n次摆动为起始，经过一个周期的摆动后，为第n+1次，则第n次摆动到最低点时的速度是由第n次摆动最高点处的势能转成的动能决定的，为：

(4)

式中：vn为第n次摆动到最低点时的水平速度；An为第n次摆动的振幅。

第n次摆动一个周期消耗的能量En为：

En=Fn×4An

(5)

式中Fn为第n次摆动所受的风阻力，风速暂取最低点风速，一般为0.5vn。

根据能量守恒定律，第n+1次摆动高度hn+1为：

hn+1=(mghn-En)/(mg)

(6)

第n+1次摆动的振幅An+1为：

(7)

4 相对运动周期数量及水平距离

因同塔多回线路悬挂异种导线，存在弧垂差异及摆动初始振幅的差异，在若干个周期后，两相导线发生相对摆动。

悬挂在同塔多回杆塔的水平两相导线均在初设振幅处开始摆动，摆动的速度与时间呈正弦函数分布，两回导线的摆动周期分别T1和T2，因异种导线的摆动周期的差异致使其摆动周期T1和T2的差异，摆动的步调不一致，当摆动若干次后，两相导线的摆动相位互差半周期后，完全相对摆动。则出现相对摆动的周期数量N为：

N=0.5T1/(T1-T2)

(8)

第N次摆动后，两相导线相向摆动，导线间水平距离d为：

d=D-AN1-AN2

(9)

式中：d为第N次摆动导线相向摆动时的水平间距；D为塔头两相导线的水平距离；AN1、AN2分别两相导线第N次摆动的振幅。

5 计算结果

5.1 摆动周期及相向摆动的周期数量

本文计算档距从200～900 m不同档距下两种导线的摆动周期，JL/G1A-400/35导线的弧垂大于JL/G1A-300/25导线，其摆长也相应较大，其摆动周期也略大，随着档距的增大，摆动周期的差异越来越大，两种导线的不同步性越发凸显。两种导线的摆动周期见图2。

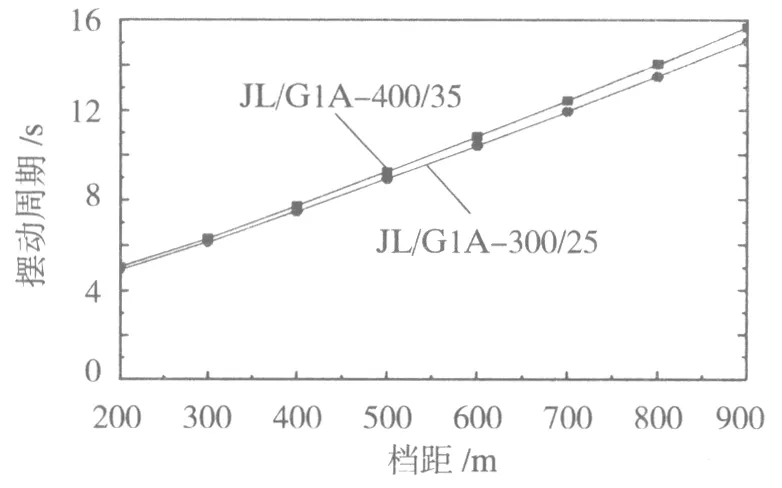
图2 两种导线的摆动周期

两种导线随档距增加，摆动周期的差异越大，两种导线发生相对摆动所需的周期数就越少，且呈现饱和趋势，当档距超过600 m后，相向摆动周期数趋于稳定，固定在13个周期，见图3。

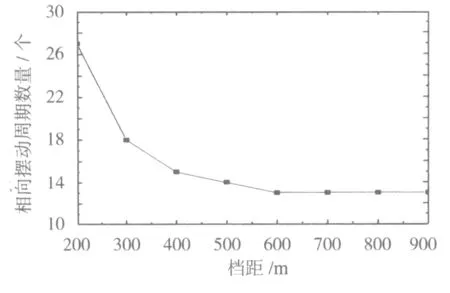
图3 两种导线的相对摆动周期数量

5.2 摆动振幅及相间水平距离

本文计算档距从200～900 m不同档距下两种导线的摆动幅值衰减曲线。

两种导线初始摆动振幅随档距变化曲线见图4。从图4可见，随着档距的增加，线路弧垂呈指数增加，初始摆动幅值亦随之增加。JL/G1A-300/25导线的初始摆动振幅略大于JL/G1A-400/35导线。两种导线摆动幅值衰减曲线见图5。

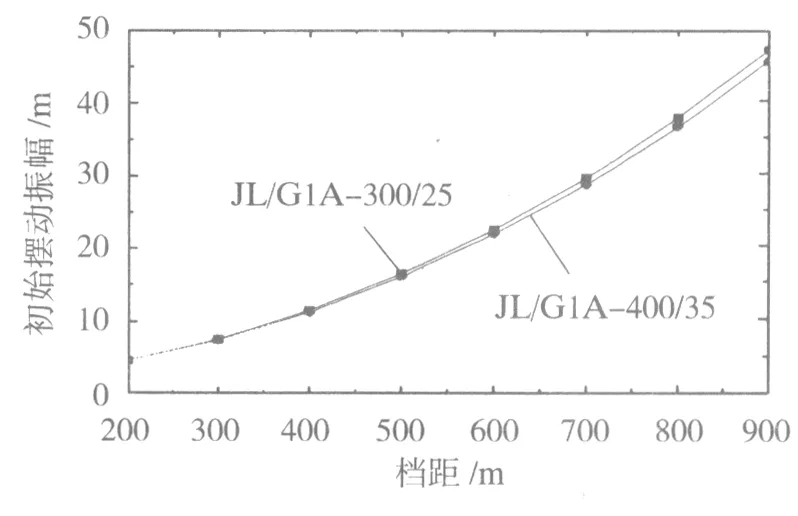
图4 两种导线初始摆动振幅随档距变化曲线

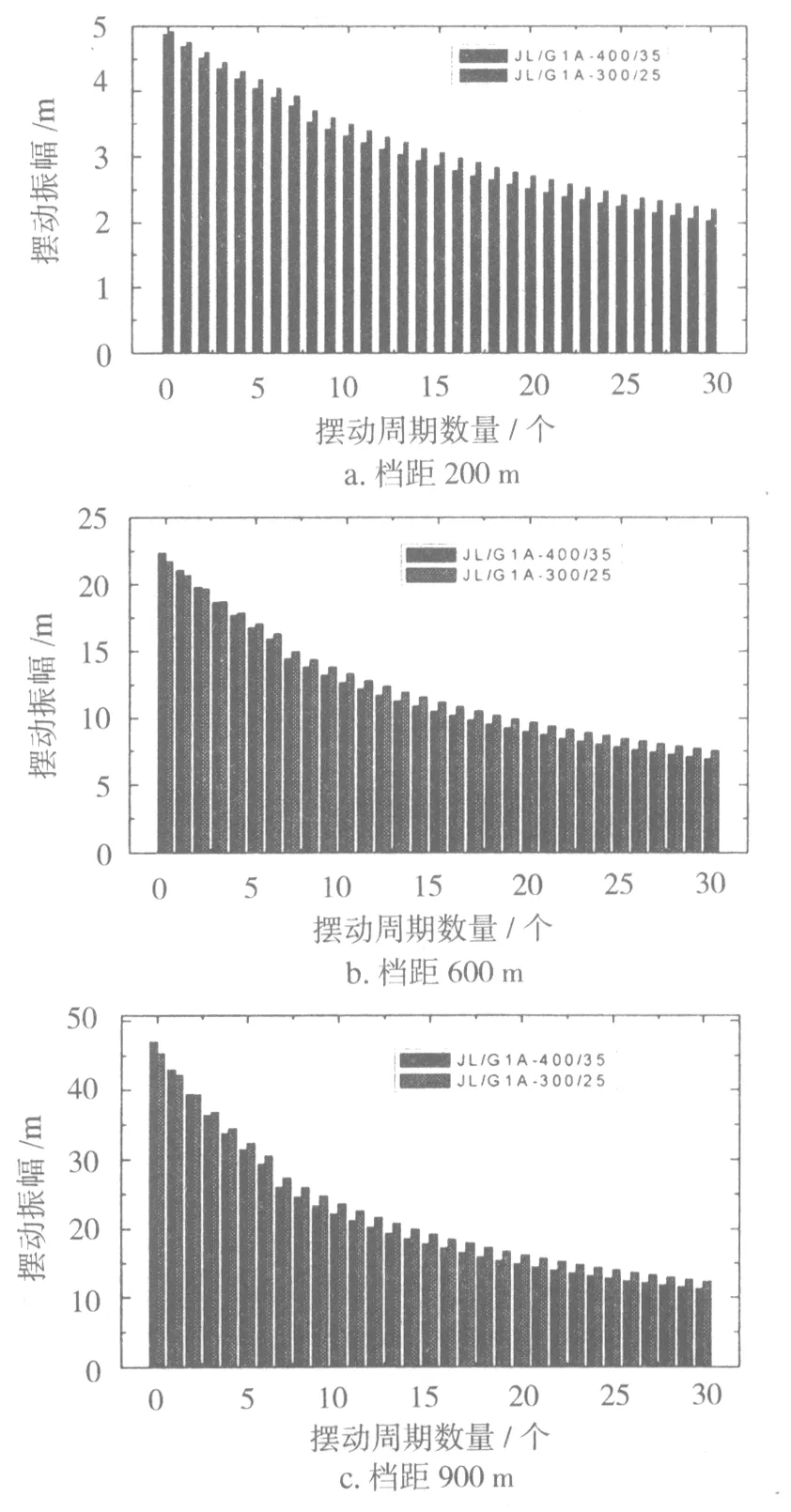
图5 两种导线摆动幅值衰减曲线

图5分别给出了档距为200 m、600 m和900 m时随着摆动周期数量的增加，摆动振幅的变化曲线，从图5可以看出，无论档距大小，随着摆动周期数量的增加，能量的诸次衰减，摆动的振幅呈现衰减趋势，且逐渐趋于饱和。档距为200 m时，摆动振幅衰减一半所需摆动周期为21个，档距为600 m时，振幅衰减一半所需周期为14个，档距为900 m时，振幅衰减一半所需周期为9个，可见，随着档距的增大，摆动振幅呈现快速衰减的趋势。

不同档距不同步摆动后相间距离见表2。

表2给出了档距从200～900 m变化时，JL/G1A-400/35导线与JL/G1A-300/25导线发生相对摆动后的相间距离。GB 50545—2010《110 kV～750 kV架空输电线路设计规范》 规定，档中操作过电压间隙为2.1 m。当档距为200 m、300 m时，两种导线发生不同步摆动时，相间距离满足规范要求2.1 m的要求；当档距超过300 m时，发生不同步摆动时相间距离不满足间隙要求，通过增加铁塔上横担长度的方式在小档距的情况可以解决间隙不足的问题；当档距过大时，该方式不再经济合理，不可采用异种导线架设方案。

表2 不同档距不同步摆动后相间距离

6 结论

本文通过建立架空线路导线摆动物理模型及摆动幅值衰减迭代算法，分别计算了2×JL/G1A-400/35、2×JL/G1A-300/25导线在不同档距下摆动周期、摆动振幅、相向摆动周期数量、不同步摆动相间距离等，结果表明：导线弧垂差异引起摆动周期差异，随着摆动的持续，摆动步调差异越来越大，在经过若干周期后发生相对摆动。

当档距为200 m、300 m时，两种导线发生不同步摆动时，相间距离满足规范要求，当档距超过300 m时，发生不同步摆动时相间距离不满足间隙要求，通过增加铁塔上横担长度的方式在小档距的情况可以解决间隙不足的问题；当档距过大时，该方式不再经济合理，不可采用异种导线架设方案。