基于Walker模型的新型钛合金疲劳裂纹扩展参数分布特征分析
白 旭,王 珂,赵春阳,屠本阳
(江苏科技大学 船舶与海洋工程学院, 镇江 212100)
耐压球壳作为载人潜水器的重要组件,一方面为潜器提供浮力,另一方面保证技术人员以及仪器设备的水下安全,在整个系统中起到了决定性的作用.基于工作环境等因素的考虑,耐压壳体的制作材质大多选用了钛合金,在潜水器的下潜过程中承受的循环载荷将引起其疲劳破坏.大多情况下,结构疲劳分析采用确定性的方法进行,然而不论是材料特性、载荷本身等都具有不确定性的特征,而这些特征正是影响疲劳寿命的不确定性因素.针对这些疲劳裂纹扩展过程中存在的不确定性,已有大量的学者采用可靠性理论对裂纹扩展过程进行了分析,但其裂纹扩展过程中的不确定材料参数特征的研究还很缺乏,而这极大地影响了可靠性分析的精确性.
为了解决不确定材料参数对于裂纹扩展中的可靠性的影响.一些学者提出了可靠性理论与裂纹扩展理论相结合的办法并开展了疲劳裂纹扩展模型的研究.文献[1]通过改进的McEvily模型给出了钛合金耐压球壳的疲劳可靠性模型,在模型中对随机变量的统计特征进行分析的基础上,采用重要样本法得到了耐压球壳的可靠性指标及失效概率.文献[2]研究了结构系统可靠性分析方法,建立了结构可靠性分析模型,得到了求取结构系统疲劳主要失效模式的方法,并讨论了系统失效概率的计算问题.而在可靠性极限状态方程的建立时,必须考虑裂纹扩展模型对于其失效概率的影响.文献[3]针对金属材料疲劳小裂纹扩展特点,在改进疲劳寿命预报统一方法的基础上对裂纹长度及小裂纹门槛值进行了进一步修正.文献[4]进行了3种应力水平下2024-T62铝合金的疲劳裂纹扩展试验,利用试验数据对疲劳裂纹扩展的分散性进行了统计分析,认为其疲劳裂纹扩展试验数据服从对数正态分布.文献[5]将裂纹扩展率分子项的幂指数由固定值改为变量,使得该模型具备对不同材料的裂纹扩展进行预报的能力.文献[6]通过对不同温度下6151-T6合金的研究,获得了一种基于可靠性理论的裂纹扩展速率表达式,为预测6151-T6铝合金构件的安全寿命提供依据.文献[7]对新的裂纹扩展速率模型中确定参数的工程方法进行了研究,并与多种合金的实验结果进行了比较.文献[8]进行了应力比对Ti-6Al-4V小裂纹疲劳扩展影响的系统研究,认为根据裂纹尺寸绘制应力比对小裂纹扩展速率有适度的影响.
概率分布模型的确定是对不确定材料参数进行分布特性研究的基础,其分布特性可以体现载荷与材料存在的分散性.文献[9]通过对16MnR压力容器热轧钢三点弯曲带缺口试样的低周疲劳实验得到了低周疲劳裂纹萌生寿命服从对数正态分布.文献[10]研究了疲劳裂纹损伤对结构极限强度的影响,认为裂纹分布位置的差异会导致不同程度的极限强度退化.文献[11]提出了在恒定振幅和可变振幅载荷下疲劳裂纹扩展分析中不确定性概率方法,采取降维技术分析疲劳裂纹扩展中的不确定性.文献[12]利用概率统计理论建立了p-da/dN-K成组法,并与a-N统计法作了对比研究,认为其与试验结果符合较好.文献[13]在传统威布尔可靠性分析和基于支持向量机的图估计法的基础上,开发了带有可视化界面的威布尔分布参数确定程序.
与Paris模型相比,Walker模型能很好地对裂纹稳定扩展阶段进行预报,其形式简单、参数较少.因此,文中将疲劳裂纹扩展理论作为基础,基于Walker裂纹扩展模型得到不确定性材料参数n、m、C,应用概率统计中的正态分布及两参数威布尔分布描述其分散性和分布特性,为钛合金疲劳裂纹扩展可靠性研究提供依据.
1 疲劳裂纹扩展模型参数的确定
1.1 钛合金疲劳裂纹扩展速率试验
裂纹扩展速率试验是高循环低载荷的一种试验,属于线弹性范围内的疲劳裂纹扩展速率试验.目前主要基于线弹性断裂力学理论,使用应力强度因子来描述疲劳裂纹扩展速率,并认为裂纹扩展速率由应力强度因子范围唯一确定.在室温环境下进行,得到钛合金在不同应力比下的疲劳裂纹扩展速率(ΔK-da/dN)曲线.
试样根据GB/T 6398-2000《金属材料疲劳裂纹扩展速率试验方法》进行CT(compact tensile)试样加工制备,试样宽度W=60 mm,试样厚度B=25 mm,两孔跨距S=75 mm,加力孔直径D=12.5 mm.新型钛合金分为5个不同载荷比进行试验,试样如图1.

图1 CT试样Fig.1 CT specimen
钛合金疲劳裂纹扩展速率试验在江苏科技大学结构力学实验室进行,试验机和引伸计的精度均满足国标GB/T 6398-2000《金属材料疲劳裂纹扩展速率试验办法》和美国标准ASTME649《Standard Test Method for Measurement of Fatigue Crack Growth Rates》的要求,试验机型号为INSTRON,试验过程如图2,CT试件断口外貌如图3.

图2 INSTRON试验平台

图3 CT试件断口外貌


图4 不同载荷比裂纹扩展试验数据Fig.4 Test data of crack growth under different load ratios
1.2 Walker模型参数的确定
Walker模型[14]是工程应用中常用的一种描述裂纹扩展速率的数学模型,它可以对不同应力比的裂纹扩展数据进行适用,其公式为:
da/dN=C(ΔK(1-R)m-1)nR≥0
(1)
式中,m、n、C为材料常数.
Walker公式中da/dN=C(ΔK(1-R)m-1)n的对数线性化表达式为:
Y=a0+a1x1+a2x2
(2)
式中:Y=lg(da/dN),X=lg(ΔK),a0=lgC,a1=n,a2=n(m-1)
Walker模型对裂纹扩展速率是关于应力比R的修正模型,根据疲劳裂纹扩展速率da/dN和应力强度因子幅值ΔK的试验数据,可作不同应力比下的裂纹扩展关系拟合曲线,进而得到C、n、m的取值,结果见表1.
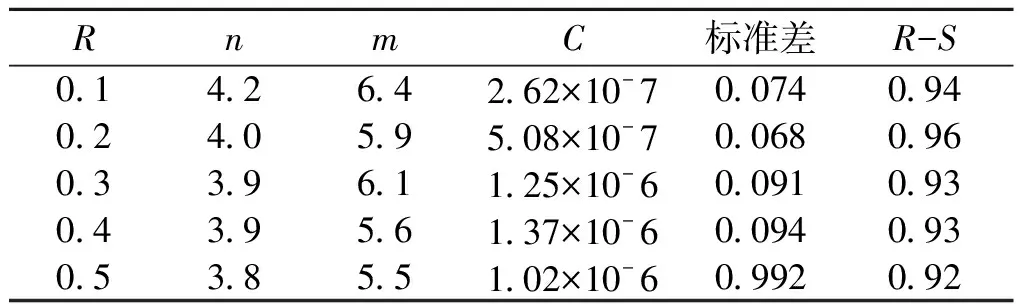
表1 Walker模型下的n、m、C数值统计表Table 1 Numerical statistical tables of n, m andC under Walker model
由表1可以看出,Walker模型的参数拟合在不同载荷比下其线性相关系数均为0.9以上.Walker裂纹扩展模型的材料参数n、m随着应力比的增加而减小,均值分别为3.96和5.90,C随着应力比的增加而增加,其均值为8.82×10-7.
2 两种分布模型的参数估计
2.1 正态分布模型
2.1.1 线性相关系数检验
若随机变量x服从正态分布,第P个数值xp与此随机数服从标准正态分布,标准正态偏量up存在线性关系:xp=A+Bup,根据平均秩理论,即p=1-i/(n+1),将其序数i代入,算出超越分布函数的估计值pi,再求出相应的标准正态分布变量取值ui,最后将(xi,ui)进行线性回归.其中线性相关系数定义为:
(3)
线性回归方程是由最小二乘法拟合得到的,xp=A+Bup中的A和B分别为:
(4)
(5)
2.1.2 正态分布的参数估计
正态分布采用点估计的数字特征进行均值和方差的计算,如式(6、7),用子样的数字特征来估计与之对应的母样本的数字特征.
(6)
(7)

2.2 威布尔分布模型
2.2.1 线性相关系数检验
假设数据T服从双参数威布尔分布[15],那么总体T的分布函数为:
(8)
样本ti(i=1,2,…,n)是来自总体T的样本,将数据[ti,F(ti)](i=1,2,…,n)代入式(8),并连续两次取对数得:
(9)
令
(10)
则式(10)可变为yi=A+Bxi,通过最小二乘法求出回归系数.
2.2.2 威布尔参数估计
由相关系数A、B可得威布尔参数的点估计值:

(11)
(12)
3 基于Walker模型的参数分布特征分析
3.1 Walker模型参数的正态分布特征
根据正态分布的点估计法可由式(8、9)求得参数n、m、C的均值和方差,并由此得到正态偏量u的取值范围,具体数值见表2.由表2中标准正态偏量up得到不确定材料参数n、m、C的正态分布线性回归方程的拟合曲线,如图5~7.

表2 Walker模型下的n、m、C正态偏量取值Table 2 Value of n, m and C normal skewers under Walker model
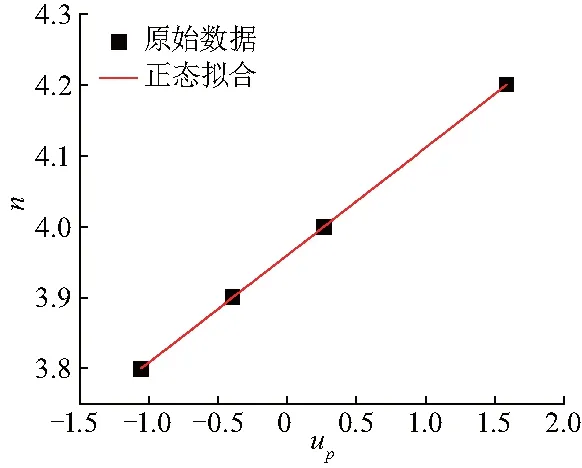
图5 参数n的正态分布拟合Fig.5 Fitting the normal distribution of parameter n
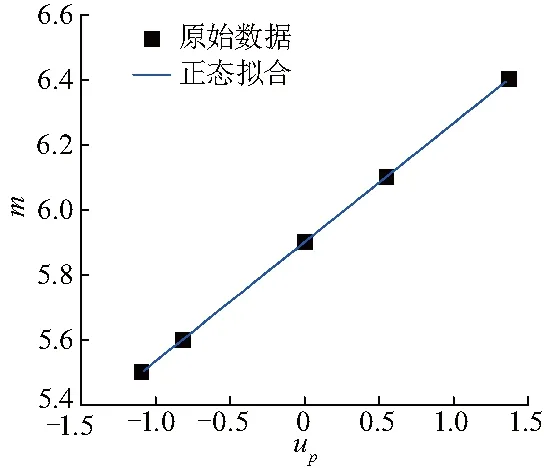
图6 参数m的正态分布拟合Fig.6 Fitting the normal distribution of parameter m
Walker裂纹扩展模型中的不确定材料参数n的正态分布回归方程xp=A+Bup中,A=3.96,B=0.151 7,线性相关系数r=0.97,标准差为8.504×10-16;不确定材料参数m的正态分布回归方程xp=A+Bup中,A=5.92,B=0.367 1,线性相关系数r=0.97,标准差为1.147×10-15;不确定材料参数C的正态分布回归方程xp=A+Bup中,A=8.82×10-7,B=4.788×10-7,线性相关系数r=0.99,标准差为3.768×10-22.

图7 参数C的正态分布拟合Fig.7 Fitting the normal distribution of parameter C
3.2 Walker模型参数的威布尔分布特征

图8 参数n的威布尔分布拟合Fig.8 Weibull distribution fitting of n

图9 参数m的威布尔分布拟合Fig.9 Weibull distribution fitting of m

图10 参数C的威布尔分布拟合Fig.10 Weibull distribution fitting of C
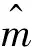
钛合金材料在Walker裂纹扩展模型中的材料参数n、m、C的分布特征拟合结果分别如表3~5.

表3 Walker模型下的材料参数n拟合结果Table 3 Fitting results of material parameter nunder Walker model

表4 Walker模型下的材料参数m拟合结果Table 4 Fitting results of material parameters munder Walker model

表5 Walker模型下的材料参数C拟合结果Table 5 Fitting results of material parameter Cunder Walker model
4 结论
(1) 基于疲劳裂纹扩展理论及试验数据,通过对Walker模型进行双对数化处理得到了不确定性材料参数,该拟合参数线性相关系数都在0.9以上,可作为特征性分析的有效数据.
(2) 在Walker计算模型下,不确定材料参数n,m,C的正态分布线性相关系数均高于两参数威布尔分布,并且不确定性材料参数C在威布尔分布下的统计规律中,线性相关系数为0.69,表现出了较大的分散性.因此,应优先考虑正态分布描述其分布特性.

